一类网络系统输入时延辨识方法研究
2013-07-20孙滨李楠石杨
孙滨,李楠,石杨
1.辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105
2.中国人民解放军65042部队72分队
一类网络系统输入时延辨识方法研究
孙滨1,李楠1,石杨2
1.辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105
2.中国人民解放军65042部队72分队
1 引言
网络控制系统(NCS)是一种全分布式、网络化实时反馈控制系统,是一定区域现场的传感器、控制器、执行器和通信网络的集合,这种网络化的控制模式能够共享信息资源,具有易于扩展、易于维护、高效率、高可靠性等优点。但是,网络控制系统存在的一个主要问题是:由于网络是时分复用的且带宽有限,信号在控制器到执行器之间的前向通道以及传感器到控制器之间的反馈通道的传输会产生时延,这个时延的长短与网络的协议、传输量、传输距离等诸多因素相关,具有显著的不确定性,将给网络控制系统的建模、控制和优化带来很大困难,甚至影响系统的稳定性[1-2]。传统的网络时延辨识方法,包括各种非线性观测器方法(如变结构观测器、自适应观测器等)、最优滤波等,这些方法的共同特点是在概率和统计意义下研究问题,需要预知系统的先验信息(如噪声的统计特性),并且普遍存在算法收敛速度慢等缺点,难以为系统的建模和控制提供实时有效的信息[3-5]。所以寻找一种快速可靠的辨识方法分析、估计网络控制系统中的各种时延,是控制工程领域研究的一个热点和难点问题。
本文针对网络控制系统、分布式控制系统等时间延迟系统(TDS)存在的一类输入信号时延的辨识问题,在分布函数理论框架下,用输入-输出卷积方程描述系统,并基于代数辨识理论设计了一种快速在线辨识时延的方法,在理想条件和噪声条件下通过仿真实验验证了这个方法的有效性。
2 基于分布函数辨识的基本原理
2.1 分布函数理论简介
为了给后面的辨识方法设计作准备,首先介绍分布函数理论的一些基本知识。
定义1具有紧支集的无限次可微函数构成的空间称为一个基本空间D=C∞(ℝN)。
定义2广义函数是定义在基本空间D上的连续线性泛函。

为了使广义函数也像普通函数那样可以局部化并具有支集,可以定义一个平滑函数α(t)与一个分布函数T的乘积[7]。
定义3广义函数T取零值的最大开集的余集称为它的支集,记为suppT。
定义4若对于支集在某一开集A中所有α(t)都有α(t)T=0,则称T在A中为0。

2.2 代数辨识的基本原理
连续系统参数的代数辨识方法是建立在线性系统的模理论、微分代数、算子运算等理论基础上的一种新的辨识理论体系,已经在参数辨识、故障诊断、信号处理等领域展开了越来越多的研究和应用,与传统的观测器和卡尔曼滤波方法相比,这种方法具有辨识速度快、不需要预知噪声的统计信息、鲁棒性好等优点[7-8]。
基于分布函数的时延(参数)辨识是在代数辨识的基本框架下,在时域或算子域(复频域)通过一定的代数运算(求导或乘法)消除掉方程或模型中的一些扰动或初始条件等未知项,再利用分布函数的特点和性质得到待辨识参数的显式表达式[9-10]。具体的辨识过程主要分为三个步骤:
(1)首先,将系统模型中包含不确定项或待辨识参数的部分用分布函数λ表示,且λ=R*ω,其中R是微分算子,ω是量测信号构成的矢量。然后在分布函数意义下,通过卷积运算建立系统的输入-输出模型,即P*λ=T,P和T都是具有支集的分布函数。
(2)在卷积输入-输出模型P*λ=T两端同时乘上一个具有光滑性质的候选函数α(t),根据泛函紧支集的性质和Schwartz定理(见定义4),消去模型中的某些不确定项,得到待辨识参数的显式表达式。即:α×(P*λ)=α×T⇒α× (P*R*ω)=0。辨识过程中,α(t)的选择取决于T的结构,一般选择α为多项式函数或指数函数。
(3)为了避免辨识结果中出现量测信号的微分,保证系统的因果性,将辨识表达式中的量测信号微分转化为迭代积分运算,最后得到需要辨识或估计的参数。
3 辨识算法设计

设一阶网络系统的非线性输入-输出模型为[8]:其中,γ0是一个常数扰动,a,b是常系数,u(t)=H(t-τ)为阶跃输入,τ为输入时延,y(t)为输出信号。

再根据分布函数T的特点选择多项式α(t)=t2(t-τ)=t3-t2τ为候选函数,且α(0)=α(1)(0)=0,α(τ)=0。将式(5)的两端同时乘上α(t),并结合δ(t)函数特点,得到时延的显式结果:

因为式(6)中出现了量测信号的二阶导数,所以要对上式两端同时进行k次积分(k≥2),最后得到时延的估计值:
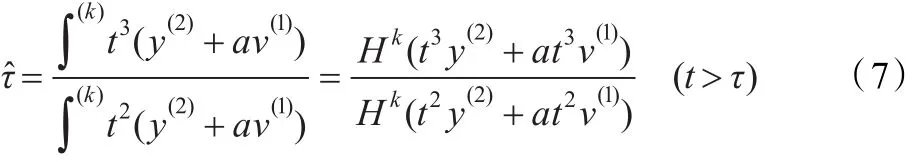
这里,Hk表示k阶重积分(k≥2)。从式(7)中可以看出时延的辨识结果τˆ只与量测信号y(t)和模型的系数a有关。上式中,根据广义函数的性质(1)~(3),可以推出:

4 数值仿真
仿真初始条件:y(0)=-0.2,τ=0.5,a=2.5,b=1。仿真时间t=2 s。
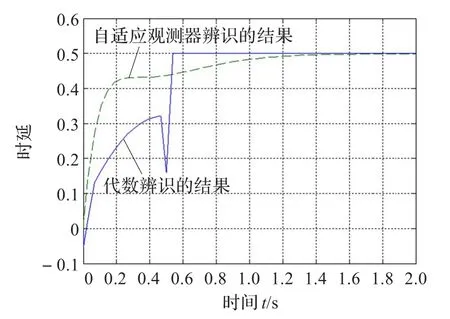
图1 时延τ的辨识结果对比(理想条件)
为了验证本文算法的有效性,将其与自适应观测器的方法对比[11]。曲线1为代数辨识的结果,曲线2为自适应观测器辨识的结果。图1为理想条件(无噪声)下时延τ的辨识结果,其中k=2。可以看出两种方法都可以得到较好的辨识结果,基于代数辨识的方法在很短的时间内(约0.5 s)就可以准确辨识出τˆ=0.5 s,而自适应观测器的方法是基于李雅普诺夫稳定性构造的,所以辨识过程是渐近,即其辨识结果是渐近趋近于真实值的,显然本文的方法快速性更好。图2是量测噪声为白噪声的条件下(ξ(t)~N(0,0.01)),两种方法的辨识结果。可以看出,虽然代数辨识的结果在初始阶段有较剧烈的变化,但是在0.5 s时仍然可以得到辨识结果,而自适应观测器的方法的辨识结果则出现了较大的偏差。图3为输入信号和输出信号均含有白噪声情况下,时延τ的辨识结果,其中k=3,4,可以看出,即使在噪声环境下,本文算法仍然可以达到快速辨识的效果,即τˆ=0.5 s,且辨识结果具有鲁棒性。而增加积分环节将使曲线变得平滑,获得更好的滤波效果,但辨识的时间有所增加。

图3 考虑噪声时τ的辨识结果
5 结束语
本文基于代数辨识理论和分布函数理论,研究了一类时延控制系统的输入时延在线辨识问题,仿真结果证明了这种方法具有良好的快速性和鲁棒性,既可以为网络控制系统等分布式控制系统的时延辨识提供很好的思路,也可以为进一步的系统建模和控制律设计打下良好的基础。
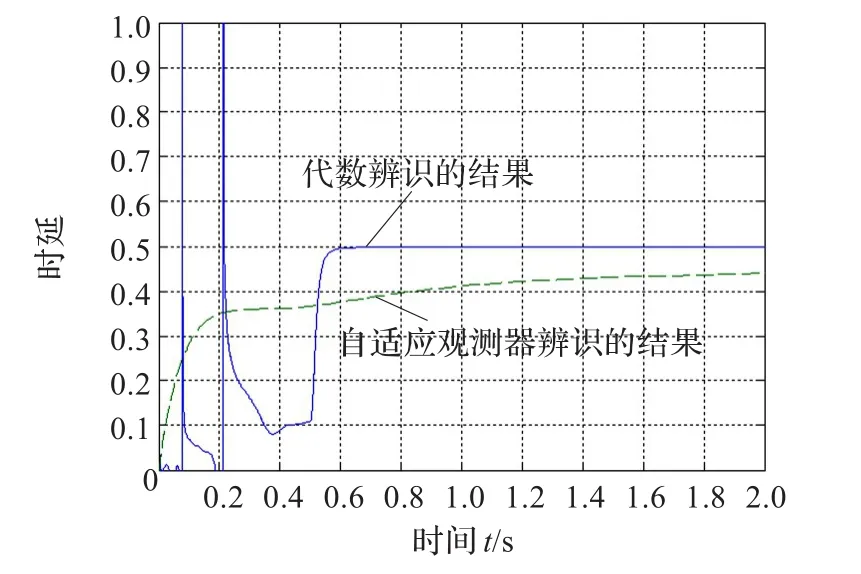
图2 时延τ的辨识结果对比(白噪声环境)
[1]孙增圻.网络控制系统分析与设计[M].北京:清华大学出版社,2009.
[2]彭晨,岳东.网络环境下不确定时滞系统鲁棒控制[J].自动化学报,2007,33(10):1093-1096.
[3]Hespanha J P,Payam N,Xu Y G.A survey of recent results in networked control systems[J].Proceedings of the IEEE,2007,95(1):138-162.
[4]Richard J P.Time-delay system:an overview of some recent advances and open problems[J].Automatica,2003,39(10):1667-1694.
[5]Sename,Olivier.New trends in design of observers for timedelay systems[J].Kybernetika,2001,37(4):427-458.
[6]Rudolph J,Frank W.An algebraic approach to parameter identification in linear infinite dimensional systems[J].AT-Automatisierungstechnik,2007,55(9):457-467.
[7]Mboup M.Parameter estimation for signals described by differential equations[J].Applicable Analysis:An International Journal,2009,88(1):29-52.
[8]Belkoura L,Floquet T,Taarit K.Estimation problems for a class of impulsive systems[J].International Journal of Robust and Nonlnear Control,2011,21(10):1066-1079.
[9]Belkoura L,Richard J P,Fliess M.Parameters estimation of systems with delayed and structured entries[J].Automatica,2009,45(5):1117-1125.
[10]Mboup M,Cedric J,Fliess M.Numerical differentiation with annihilators in noisy environment[J].Numerical Algorithms,2009,50(4):439-467.
[11]Pi-Ian M,Horta I L G,Juang J N.Linear system identification via an asymptotically stable observer[J].Journal of Optimization Theory and Application,1993,79(1):59-86.
SUN Bin1,LI Nan1,SHI Yang2
1.Faculty of Electrical and Control Engineering,Liaoning Technical University,Huludao,Liaoning 125105,China
2.72 Units,65042 Troop of PLA,China
Real time delay identification for Time Delay System(TDS),including networked control system and distributed control system etc,is a longstanding open problem in control engineering domain.An on-line and closed-loop identification method is proposed from an algebraic viewpoint to deal with the delayed input identification of networked control system in non-asymptotic distributional framework.Compared with the adaptive observer identification method in ideal condition and white noise condition,the favorable robustness and fastness properties are presented in the numerical simulations that demonstrate the effectiveness of this method.
time delay system;networked control;distribution function;identification
针对网络控制系统、分布式控制系统等时间延迟系统的时延辨识问题,在分布函数理论框架下,利用输入信号和输出信号的卷积运算建立系统的时域模型,基于代数辨识理论和分布函数的性质设计了一种快速在线辨识输入信号时延的方法。在理想条件和白噪声环境下与传统的自适应观测器方法进行对比,通过数值仿真验证了该方法具有良好的快速性和鲁棒性。
时延系统;网络控制;分布函数;辨识
A
TP273
10.3778/j.issn.1002-8331.1204-0515
SUN Bin,LI Nan,SHI Yang.Time delayed input identification of a kind of networked control system.Computer Engineering and Applications,2013,49(24):253-255.
辽宁省教育厅基金项目(No.L2010166)。
孙滨(1977—),女,讲师,主要研究领域为信号分析、智能控制等;李楠(1978—),男,博士研究生,主要研究领域为复杂系统辨识与控制;石杨(1982—),女,工程师,主要研究领域为通信工程。E-mail:lnfxsunbin@163.com
2012-04-27
2012-07-09
1002-8331(2013)24-0253-03
CNKI出版日期:2012-08-01http://www.cnki.net/kcms/detail/11.2127.TP.20120801.1654.032.html
