基于形式概念分析理论的完全格存储模型

智慧来

河南理工大学计算机科学与技术学院，河南焦作 454000

基于形式概念分析理论的完全格存储模型

智慧来

河南理工大学计算机科学与技术学院，河南焦作 454000

1 引言

格描述了对象之间的偏序关系，便于对象的聚类和层次结构的分析。近年来格论，特别是完全格理论在GPS中的坐标变换[1]、模糊故障检测[2]、机器人集群[3]、不确定性数据表示[4]等领域都有应用。在这些应用中，都需要进行格的存储与检索操作。在理论研究时，通常使用的格结构比较简单，使用邻接矩阵来存储格是完全可行的。然而，在实际应用中由于描述的对象十分复杂，构造的格结点数目众多，格结点之间的关系也更加复杂，仍旧采用邻接矩阵来存储格将耗费大量存储空间，不利于格的检索和同构判定。格的存储不再是一个无关紧要的问题，而是一个有实际应用价值的关键理论问题。

形式概念分析理论与格论有天然的联系。形式概念分析是R.Wille[5]提出的，以序论和格论为基础建立起来的，它的核心数据结构概念格是对概念以及概念之间关系的描述，由于它便于概念结构的开发和讨论，在某种意义上，概念格已经变成了一种外部认知的手段，并在人工智能领域有广泛而成熟的应用[6]。鉴于形式概念分析理论在数据分析与表示中的独特优势，本文将利用这一理论提出一个基于概念格模型的完全格存储模型。

2 基本概念

下面的基本概念均出自于Ganter B的著作“Formal Concept Analysis”[5]。

定义1一个集合M及其上的偏序关系≤形成的有序二元组(M,≤)称为半序集。

定义2令(M,≤)是一个半序集，A是M的子集，若M中的元素s满足∀a∈A都有s≤a，则称s是A的一个下界。对偶地，若M中的元素s满足∀a∈A都有s≥a，则称s是A的一个上界。如果A的所有下界组成的集合中有最大元素，则称这个元素为A的下确界，记infA或∧A。对偶地，上界集合的最小元素称为A的上确界，记supA或∨A。

定义3一个半序集(V,≤)，如果V中任意两个元素x,y的上确界及下确界都存在，则称V是一个格。如果V的任何子集的上确界及下确界都存在，则称V是一个完全格。

定义4对于完全格V的一个元素v，定义vl=∨{x∈V|x＜v}，vu=∧{x∈V|v＜x}，如果v≠vl即v不是严格小于它的那些元素的上确界，则称v是上确界不可约的，或者称v是上确界不可约元；如果v≠vu，即v不是严格大于它的那些元素的下确界，则称v是下确界不可约的，或者称v是下确界不可约元。在不区分上确界不可约元和下确界不可约元的情况下，它们统称为不可约元。

定义5a称为b的下近邻，当a＜b且没有c满足a＜c＜b，这时也称b是a的上近邻，并且记做a≺b。

定义6一个形式背景K=(G,M,I)是由两个集合G和M以及G与M之间的关系I组成。G的元素称为对象，M的元素称为属性。(g,m)∈I或gIm表示对象g具有属性m。

定义7设A是对象集合G的一个子集，定义f(A)= {m∈M|g∈A,gIm}，相应地设B是属性集合M的一个子集，g(B)={g∈G|m∈B,gIm}。如果A、B满足条件f(A)=B且g(B)=A，则称序对(A,B)为形式背景K的一个概念，A称为概念(A,B)的外延，B称为概念(A,B)的内涵。

定义8若(A1,B1)、(A2,B2)是某个形式背景的两个概念，而且A1⊆A2（等价于B2⊆B1），则称(A1,B1)是(A2,B2)的子概念，(A2,B2)是(A1,B1)的父概念，并记做(A1,B1)≤(A2,B2)，关系≤称为是概念的“层次序”。(G,M,I)的所有概念用这种序组成的集合称为概念格，记做B(G,M,I)。

定义9在一个概念格中，如果一个概念具有形式(g(f(g)),f(g))且g∈G，则称这个概念是一个对象概念；如果一个概念具有形式(g(m),f(g(m)))且m∈M，则称这个概念是一个属性概念。

定理1（概念格基本定理）概念格B(G,M,I)是一个完全格，其上确界和下确界分别是：

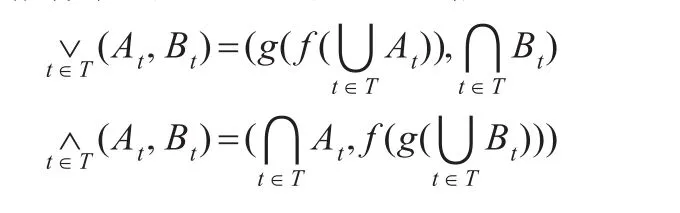
3 基于形式概念分析理论的完全格存储模式

定义10对于形式背景(G,M,I)，每一个属性子集P⊆M决定了一个二元不可区分关系IND(P)={(x,y)∈G×G|∀a∈P,I(x,a)=I(y,a)}[7]。

定义11在一个信息系统中a∈M，如果IND(M-{a})=IND(M)，则称属性a在M中是不必要的，否则，称a在M中是必要的。如果每个属性a∈M在M中都是必要的，则称属性集M是独立的，否则，称M是相依的。对于相依的属性集来说，其中包含有多余属性，可以对其约简[7]。

定义12设P⊆M，如果IND(P)=IND(M)，并且P是独立的，则称P是M的一个约简[7]。

定义13一个信息系统所有属性约简的交集称为核，核中的属性称为是核心属性。不属于任何约简的属性称为不必要属性，属于某些约简但不属于核的属性称为相对必要属性。核心属性与相对必要属性统称必要属性[8]。

根据形式背景的对偶性，可以直接得到对象纯化形式背景的概念，这里不再赘述。

定义14若形式背景(G,M,I)既是对象纯化的，又是属性纯化的，则称形式背景(G,M,I)是纯化的形式背景，简称形式背景(G,M,I)是纯化的[9]。

命题1有限格的一个元素是上确界不可约的，当且仅当它有且仅有一个下近邻；一个元素是下确界不可约的，当且仅当它有且仅有一个上近邻。

定理2在纯化形式背景中，对象概念是上确界不可约元，上确界不可约元一定是对象概念；属性概念是下确界不可约元，下确界不可约元一定是属性概念。

证明先证明定理前半部分。反证法，假设对象概念(A,B)不是上确界不可约元，即对象概念有两个或两个以上的下近邻，其中的两个下近邻记做(At,Bt)，t为指标集，t∈T。由于(A,B)是对象概念，因此存在对象g∈A使得f(g)=B。根据概念格基本定理，有B=∩Bt(t∈T)，又因为f(At)=Bt(t∈T)，则有f(g)=∩f(At)(t∈T)，因此g是可约简的，与纯化形式背景的前提矛盾，故定理成立。根据概念格的对偶原理，可知定理的后半部分成立。

定义15若完全格V的每个元素都是X(X⊆V)的某个子集的上确界，则X称为在V中是上确界稠密的。对偶地，若完全格V的每个元素都是X(X⊆V)的某个子集的下确界，则X称为在V中是下确界稠密的。

定理3若V是一个完全格，G和M是两个集合，则存在两个映射γ:G→V和μ:M→V，并且γ(G)是上确界稠密的，μ(M)是下确界稠密的。对任意的g∈G和m∈M定义关系I，gIm⇔γ(G)≤μ(M)，那么V和概念格B(G,M,I)同构[10]。

定义γ(g):=(g(f(g)),f(g))（对象概念），μ(m):=(g(m)，f(g(m)))（属性概念），则有gIm⇔g∈g(m)⇔g(f(g))⊆g(f(g(m)))=g(m)⇔γ(g)≤μ(m)，因此gIm⇔γ(G)≤μ(M)成立，可知函数γ(g)和μ(m)满足定理3。

根据上面的论述，可以从完全格V，使用映射γ、μ得到与其同构的概念格的形式背景K，并使用矩阵存储此形式背景，从而实现对完全格的存储。

算法1计算完全格的形式背景

输入完全格V；

输出形式背景K

步骤1从完全格V最小元开始向上遍历，若一个格结点只有一个上近邻，则从字母表{a,b,c,…}中取一个字母标注，标注后将这个字母从字母表中删除。

步骤2从完全格V最大元开始向下遍历，若一个格结点只有一个下近邻，则从数字表{1,2,3,…}中取一个数字标注，标注后将这个数字从数字表中删除。

步骤3若一共使用了m个数字和n个字母，则建立m行n列的形式背景K，每一个数字对应一行，每一个字母对应一列。

步骤4在完全格V中，对于每个用数字标注的格结点（假定标注的数字为i），搜索其上近邻直到最大元，若在这一过程中遇到用字母标注的格结点（假定标注的字母为j），则将K中i行j列交叉处的值修改为*。

步骤5返回K，算法结束。

应用算法1，可以将存储一个完全格转化为存储一个形式背景。存储形式背景实际上就是存储一个矩阵。

例1对于图1中的完全格V，使用算法1（标注了不可约元的完全格见图2），可以得到5行5列的形式背景K（见表1），并依据形式背景建立5×5的存储矩阵

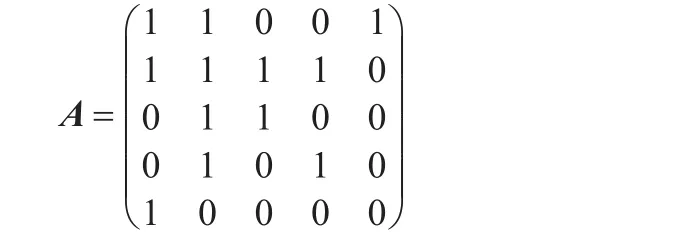
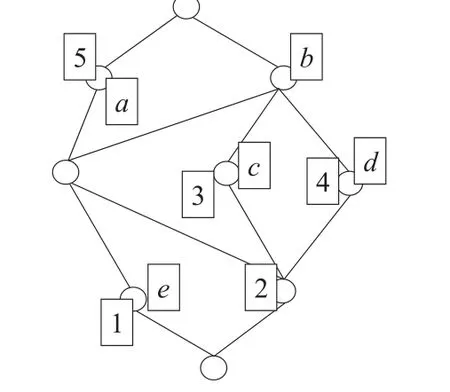
图2 标注不可约元的完全格V

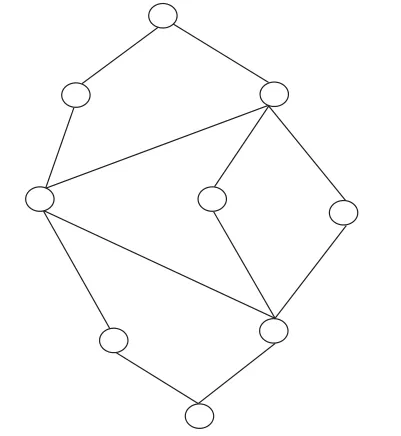
图1 完全格V

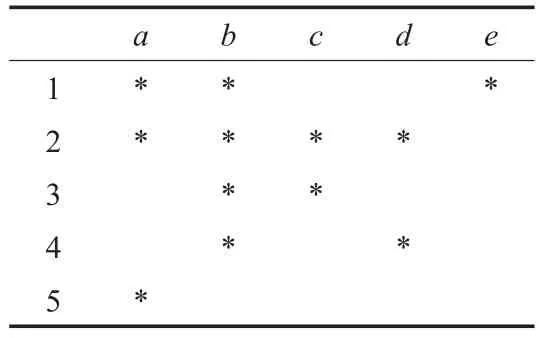
表1 形式背景K

若使用邻接矩阵存储完全格V，根据结点之间的邻接关系建立一个9×9的邻接矩阵为：

其中有12个非零元素。两种方法的存储效率对比见表2。

另一方面，本文的方法有利于提高判定完全格同构的效率。完全格同构的判定可以转化为图同构的判定，多数学者认为图的同构判定问题属于NP-完全问题[11]。利用存储矩阵通过行交换和列交换，如果能够得到相同的矩阵则可以判断是同构的。在最坏情况下交换的总次数将达到r!×c!（r为背景的行数，c为背景的列数），复杂性远远大于指数时间复杂性[12]。本文的方法降低了存储矩阵的行、列数，因此有利于实现完全格同构的判定。

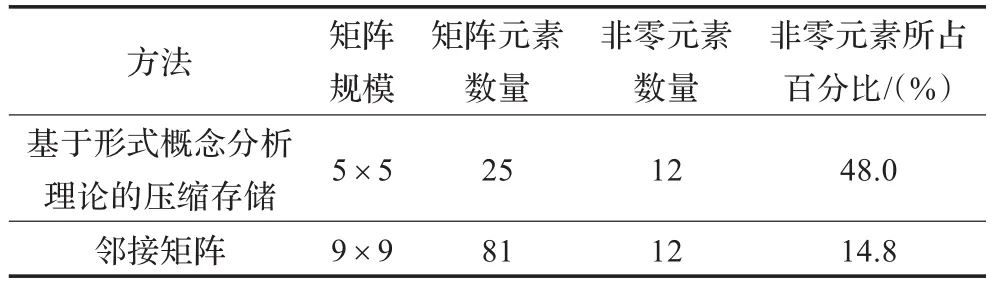
表2 存储效率对比

4 结束语

格结构在理论研究和实际应用中广泛存在，本文利用形式概念分析的理论研究完全格的存储。本文的方法只存储不可约元及不可约元间关系的信息，并不存储其他信息，与采用邻接矩阵的存储方式相比提高了存储效率，为复杂格结构的应用提供技术上的支持。

[1]Wu Chih-Hung，Su Weihan.Lattice-based clustering and genetic programming for coordinate transformation in GPS applications[J].Computers and Geosciences，2013，52：85-94.

[2]Li Bing，Liu Pengyuan，Hu Renxi，et al.Fuzzy lattice classifier and its application to bearing fault diagnosis[J].Applied Soft Computing Journal，2012，12（6）：1708-1719.

[3]XuQingzheng，WangLei.Lattice-basedartificial endocrine system model and its application in robotic swarms[J].Science China Information Sciences，2011，54：1-17.

[4]Denoeux T，Younes Z，Abdallah F.Representing uncertainty on set-valued variables using belief functions[J].Artificial Intelligence，2010，174：479-499.

[5]Ganter B，Wille R.Formal concept analysis：mathematical foundation[M].New York：Springer-Verlag，1999.

[6]Scaife M，Rogers Y.External cognition：how do graphical representations work[J].International Journal of Human Computer Studies，1996，45：185-213.

[7]梁吉业，曲开社，徐宗本.信息系统的属性约简[J].系统工程理论与实践，2001（12）：76-80.

[8]Pawlak Z.Rough sets—theoretical aspects of reasoning about data[M].Dordrecht：Kluwer Academic Publisher，1991.

[9]智慧来，智东杰.纯化形式背景及其性质研究[J].计算机工程与应用，2011，47（35）：61-62.

[10]Davey B A，Priestley H A.Introduction to lattice and order[M]. New York：Cambridge University Press，2002.

[11]Karp R M.Reducibility among combinatorial problems[M]. New York：Plenum Press，1972.

[12]李锋，李晓燕.图的同构判定算法：关联度序列法及其应用[J].复旦学报：自然科学版，2001，40（3）：318-325.

ZHI Huilai

School of Computer Science and Technology,Henan Polytechnic University,Jiaozuo,Henan 454000,China

The storage of complete lattice is an important issue in various types of applications.The theory of formal concept analysis is adopted in the storage of complete lattice.For a given complete lattice,when it is stored by using a matrix,irreducible elements are identified.This paper marks the upper and lower irreducible elements separately by using different types of signs,i.e. object labels and attribute labels,and lets them indicate rows and columns of the matrix.It ascertains the element of the matrix according to the relationship between the upper and lower irreducible elements.Compared with using adjacent matrix,this method is more efficient and suitable for application.

formal concept analysis;complete lattice;irreducible elements;storage model;concept lattice

完全格的存储是一个有实际应用价值的关键问题。在利用矩阵存储完全格时，识别完全格中的不可约元；分别对上确界不可约元和下确界不可约元用对象标签和属性标签进行标注，使得对象标签和属性标签分别对应矩阵的行和列；根据不可约元之间的关系确定矩阵中元素的值。与采用邻接矩阵存储完全格相比，该方法只存储不可约元的相关信息，能够提高存储的效率。

形式概念分析；完全格；不可约元；存储模型；概念格

A

TP18

10.3778/j.issn.1002-8331.1308-0020

ZHI Huilai.Storage model of complete lattice based on theory of formal concept analysis.Computer Engineering and Applications,2013,49（24）：1-3.

国家自然科学基金（No.60975033）；河南理工大学博士基金（No.B2011-102）。

智慧来（1981—），男，博士，讲师，研究领域：粗糙集合、本体、形式概念分析等。E-mail：zhihuilai@126.com

2013-08-05

2013-09-16

1002-8331（2013）24-0001-03

CNKI出版日期：2013-09-26http://www.cnki.net/kcms/detail/11.2127.TP.20130926.1644.001.html