高职数学两个重要极限教法探究

贾敬堂 徐爱华 张彩红

（邯郸职业技术学院，河北邯郸 056005）

高职院校的新生大多在中学阶段的数学基础较差，经初步抽查，有的班的学生高考数学成绩最高分为93分（满分为150分），最低的只有6分，这给高等数学的教学带来很多问题。如何克服困难，保证大多数学生能够学好数学，值得高职院校的数学教师研究并且要探索出一个可行的教法。

一、问题的提出

学生在学习两个重要极限时的困惑:

在给各班上课讲两个重要极限时，经常遇到学生做相关题目不能区分两个重要极限，也就是抓不住问题的实质。如何正确使用等价无穷小代换以及洛必达法则需要教师耐心细致的帮助学生用简单易行的方法来分辨。

二、问题的分析

经过与部分学生详谈，了解到有的学生产生上述困惑的主要原因是:

1.概念不清

上课不认真听讲，没注意到第一个重要极限是两个无穷小的比的极限，第二个重要极限是“1+无穷小”，指数是无穷大，且与无穷小互为倒数。

2.基础不扎实

有的学生平时很少做题，几乎不看教材。

3.缺乏自信

有的学生因为在中学阶段数学没学好，不相信自己能学好高等数学，放任自己，上课不认真听讲，甚至在课堂上交头接耳，还有的在课堂上睡觉、看与数学无关的书、玩手机，不积极回答教师提问，不积极做作业。

三、促进学生学习的方法与策略

由于高职学生的数学基础参差不齐，作为数学教师，既要照顾到基础不好的学生，同时也要考虑到部分数学基础相对较好的学生。

1.促进学习的方法

有的学生对于第一个重要极限的证明方法，经过思考后理解了。对于第二个重要极限由于一般高职教材没有涉及到证明，仅仅是一个结论:单调有界数列，必有极限。大多数学生只关心结论，但是有少数学生非常想明白这个结论是怎么证明的。

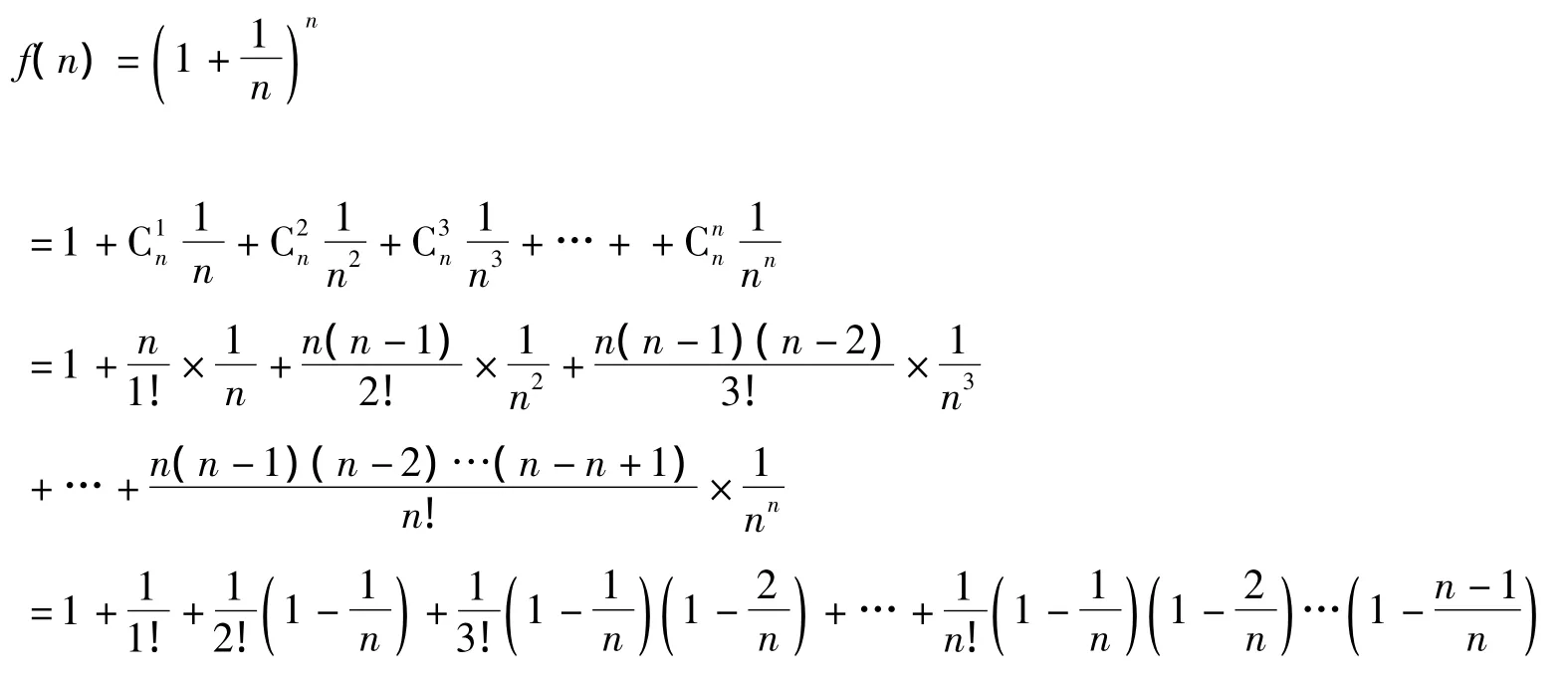
同理，可得

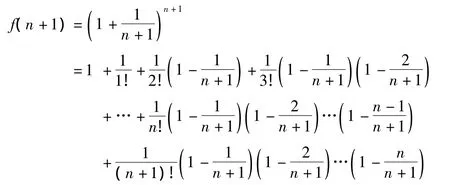
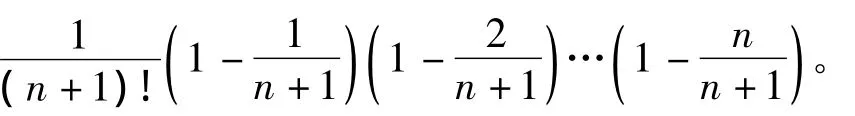
于是，得出

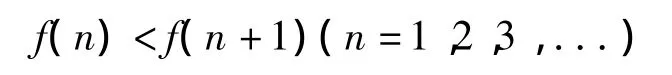
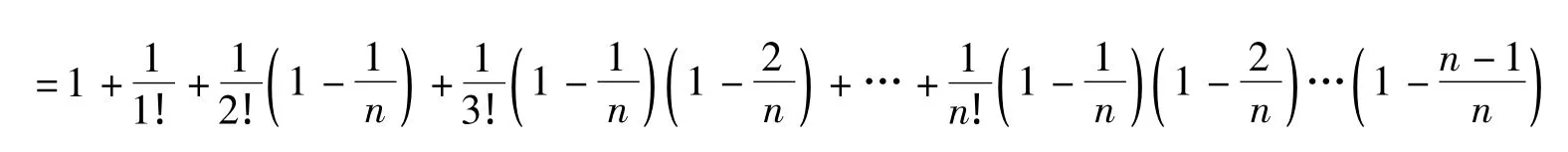
上式中每个括号内的数都小于1，于是

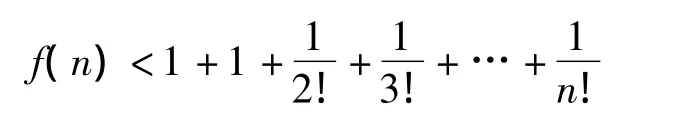
又因为 n!＞2n－1（n ＞2，n∈N），得

因此，f（n）有界。

那么e的值等于多少，实际上就是高中学过的自然对数的底，可以利用无穷级数中的幂级数

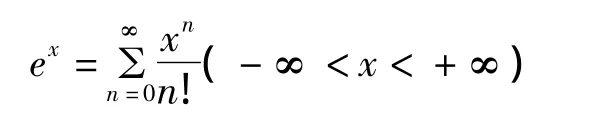
利用数学软件Mathematica，可以得到

命题得证。

另外，在教学生学习第二个重要极限时，需要教会学生注意适当变形。

善于发现学生的优点，适时加以鼓励引导，参考上述方法引导学生继续探究、找规律、猜想，如果方法得当，可以得到

学生学习信心来源于自身，同时也与周围的同学、教师的鼓励有关。数学较差的学生自信以后，就可以由小成功导致大成功。

2.促进学习的策略

对于高职学生，有时需要激发学生兴趣，充分利用各种有利条件调动学生学习数学的积极性，增强数学与实际生活的联系，避免枯燥无味的讲解。既要满足学习好的学生学习需求，又要保证学习差的学生不能掉队，一直是我们高职数学教师的责任和基本要求。

例如，在使用等价无穷小代换时，切记不要在加减运算时使用，但在乘除运算时可以考虑使用，这样使用可以简化极限运算。

常见的等价无穷小代换，当x→0时，

错误使用等价无穷小，结果往往是错误的。

四、结束语

针对高职院校学生高等数学基础相对较差，以及高职院校更注重数学在实践中的应用，在实际教学中，应教会学生吃透教材，并且结合实际，进行口诀化教学，尽量使用短小精悍的语言，让学生尽快掌握并能熟练应用。

［1］于坚.高等数学探究性学习模式的研究与实践［J］.教育与职业，2006，（11）

［2］韦美雁.第二个重要极限的一个推广［J］.湖南科技学院学报，2008，（12）