基于CFD的选粉机分级过程数值模拟

刘校兵，刘传慧，刘 平，綦海军

（西南科技大学制造科学与工程学院，四川 绵阳 621010）

涡流空气选粉机是建材、矿物加工、化工、粮食加工、食品、医药等行业粉体制备系统中非常重要的设备之一[1]。选粉机内颗粒的分级是将达到细度要求的细颗粒及时筛选出来，同时将粗颗粒返回磨机中进行重新粉磨的过程。研究选粉机的分级过程有助于了解颗粒在分级区内运动特性，从而有助于指导选粉机结构改造和操作参数的优化控制。

涡流空气选粉机分级室结构和工作原理如图 1所示，颗粒进入分级室以后，分级过程发生在导风叶片与转子叶片之间的环形区域，即分级区[2]。在分级区内，颗粒在水平方向主要受到了沿转子径向向内的气体曳力D和向外的离心力F，转子在转动过程中，带动气流旋转，细颗粒受到的气体曳力大于其受到的离心力，在气流拖拽下进入转子内部，最后从出口排出作为成品被收集，而粗颗粒受到的气体曳力小于离心力，被抛向转子外围，受到导风叶片内壁或壳体碰撞后失去动能，掉入粗粉返料锥。根据此二力平衡，可以得到分级粒径公式[3]。见式（1）。

图1 涡流选粉机转子结构与颗粒受力

式中，d50为分级粒径，m；Q为风量，m3/h；v为气体运动黏度，m2/s；ρp为颗粒密度，kg/m3；ρg为气体密度，kg/m3；H为转子高度，m。

在前人的研究中，主要从理论推导[4-5]和流场模拟[6-7]的角度分析了选粉机的流场特性，而对于分级过程的数值模拟，国内外报道较少。为了考察颗粒在选粉机分级区的分级过程，研究颗粒的运动特性，本文作者以涡流空气选粉机SLK3500为研究对象，对分级室转子分级区平面进行了二维建模，对模型进行网格划分和气固两相流求解，得到了颗粒在分级区内运动轨迹和实时运动规律，为研究颗粒运动仿真和优化选粉机结构提供了方法和数据基础。

1 计算模型与求解方法

1.1 物理模型与边界条件

根据涡流空气选粉机分级室实际参数，构造了选粉机分级室平面模型（图2），模型主要包括气流入口、导风叶片、转子叶片、旋转区域和气流出口。对模型进行网格划分（图3），采用四面体与六面体网格结合划分的方法，并在导风叶片与转子叶片等重点观察区域进行网格加密，以提高计算精度。在边界条件的定义中，气流入口采用速度入口（velocity-inlet），出口为自由出口（outflow），转子叶片区域为转动区域，采用移动坐标系（MRF）来模拟转子转动。根据实际操作参数，定义入口流速为8.2 m/s，定义转子转速为60 r/min。

1.2 计算模型与控制方程

图2 流场物理模型

图3 流场网格模型

表1 计算模型及离散格式

计算模型及离散格式如表1所示，采用离散相模型（DPM）来模拟选粉机内颗粒的释放和气固耦合，由于涡流空气选粉机内固相体积分数远小于10%，采用拉格朗日离散相模型计算。对分级区内流场首先进行气相流场的求解，当得到一个收敛的连续相流场后再运用颗粒轨道模型模拟颗粒的运动轨迹。为了再现涡流空气选粉机内部的颗粒轨迹，本研究采用相间耦合的随机轨道模型，在该模型中，把流体作为连续介质，颗粒当作离散介质。随机轨道模型可以跟踪拉格朗日坐标系下的颗粒轨迹，同时还可考虑颗粒运动对气相湍流的影响。由于选粉机内的颗粒浓度为1.2 kg/m3左右，浓度相对较小，因此采用该模型能较好地跟踪颗粒的运动。

DPM（dust production model）离散模型是国际上公认比较成熟的颗粒释放模型[8-9]，可以较好地用于定义涡流空气选粉机内水泥生料颗粒的注射。根据作用在颗粒上的力平衡分析，离散相颗粒在Lagrangian坐标系下的运动方程如式（1）～式（3）。

式中，t为时间，s；u为气流速度，m/s；up为颗粒速度，m/s；gx为重力加速度在x方向分量，m/s2；ρp为颗粒密度，kg/m3；ρ为气体密度，kg/m3；Fx为单位质量颗粒受到的力在x方向的分量，m/s2；μ为气流运动黏度；Re为颗粒雷诺数；CD为曳力系数。

雷诺应力模型（RSM）是基于各向异性的湍流模型，雷诺应力输运方程具有更强的描述复杂湍流的能力[10]。其输运方程模型如式（4）。

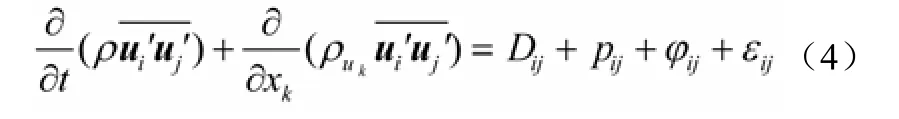
等式左边两项分别为应力随时间变化率和对流项；右边Dij为湍流扩散项；pij为应力产生项，可忽略；φij为压力-应变耦合项；εij为黏性耗散项。其中φij及εij见式（5）、式（6）。

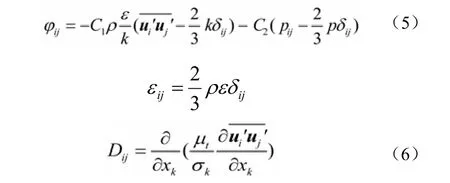
式中，ui'，uj'为气流脉动速度矢量分量；t为时间；ρ为气流密度；xk为笛卡尔坐标分量，k为湍流动能；uk为速度时均速度分量；μt为湍动黏度；C1和C2为常数；k为湍动能；ε为湍能耗散率；其它符号及其表示意义详见文献[11]，这里不再赘述。

2 模拟结果分析

2.1 稳态模拟与结果分析

对上述选粉机分级室平面模型首先进行气相单相计算，待气相流场的计算收敛之后，加入DPM离散相颗粒进行气固耦合计算。在离散相颗粒喷射源定义中，以气相入口为颗粒释放入口，颗粒粒径为单粒径分布，共定义10组，分别为10 μm、20 μm、30 μm、··、100 μm。气固耦合模拟计算后，分别观察不同粒径的颗粒在分级过程中轨迹的变化规律，如图4所示。

在图 4所示的颗粒粒径与运动轨迹变化关系中，可以看出，颗粒的分级是在导风叶片与转子叶片的环形区（即分级区）发生的。不同粒径大小的颗粒随气流进入环形区后，运动轨迹发生改变，粒径较小的颗粒（10～30 μm）随气流跟随性较好，在环形区内颗粒运动轨迹流畅，颗粒在环形区内停留时间在1～2 s后进入转子内部，完成分级；粒径较大的颗粒（50～80 μm）随气流跟随性较差，在环形区内颗粒运动轨迹紊乱，并且在环形区内长时间盘旋，造成轨迹变长，颗粒在环形区停留时间增大到3～4 s，最终进入转子内部完成分级的颗粒轨迹数量也较少。根据前文理论分析，在涡流空气选粉机分级室二维平面内，颗粒在环形区内受到气体曳力和离心力作用，由受力分析可知，颗粒所受气体曳力与气体流速有关，与颗粒粒径无关。粒径较小的颗粒受到的离心力小于其受到的气体曳力，颗粒在气体曳力拖拽作用下，进入转子内部的概率较大，即分级效率较高；而粒径较大的颗粒则受到的离心力大于其受到的气体曳力，颗粒受离心力影响，进入转子内部的概率较小，分级效率较低。因此，若想使粒径较大的颗粒进入转子内部，需要降低转速，使颗粒受到的离心力减小。反之，若想得到更细的产品，则需要提高转速，增大颗粒的离心力。由此可以看出，对颗粒在分级区内的理论受力分析与模拟得到的颗粒运动轨迹和颗粒的分级过程较为吻合。

在考察颗粒运动轨迹的基础上，对不同粒径的颗粒在分级区内的分级效率作了数值模拟分析。分级效率表征的是颗粒在分级区内完成分级最终进入转子内部被收集为成品的概率。因此，在气固两相流出口处对颗粒进行捕捉，捕捉方式为逃逸（escape），用以统计经过分级之后流经出口被收集到的成品颗粒数量。用计算出的逃逸的颗粒数量与入口喷射源颗粒数量的比值来表示该粒径颗粒的分级效率大小。同样以上述 10组颗粒为跟踪对象，绘制出如图 5所示的颗粒粒径与分级效率的关系曲线。

从图5可以看出，粒径较小的颗粒（如10 μm）分级效率较高，在90%以上，随着粒径的增大，颗粒的分级效率呈明显的下降趋势，但下降的过程为非线性变化。当颗粒粒径达到80 μm以后，分级效率已小于10%，而粒径＞100 μm的颗粒分级效率基本为 0。因此，粒径较大的颗粒进入转笼内部被收集为成品的概率较高，反之较低，与理论分析相符。以进入粗粉和细粉的概率相等时的颗粒粒径为切割粒径大小。在该模拟工况下，粒径42 μm的颗粒分级效率为 50%，表明颗粒进入粗粉和细粉的概率各为50%，因此，在该模拟工况下，选粉机切割粒径为 42 μm。

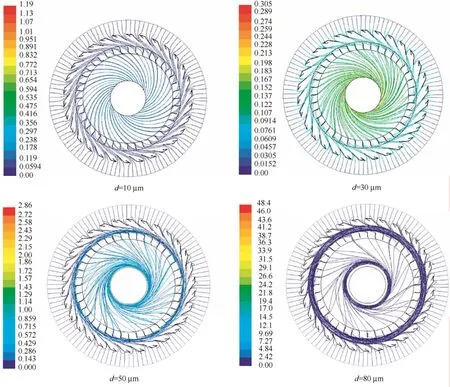
图4 稳态计算不同粒径颗粒轨迹

图5 不同粒径颗粒分级效率

2.2 非稳态多粒径颗粒运动实时仿真

对颗粒运动进行稳态仿真，得到了颗粒的运动轨迹和分级效率的变化规律，但不能反映颗粒在此过程中的实时运动，因此对颗粒运动进行非稳态仿真，对颗粒在分级区内运动状态进行了实时跟踪，利用宏定义在每个计算时间步完成之后将颗粒的停留位置以图片形式自动保存并输出，以考察颗粒的实时运动，结果如图6所示，颗粒的颜色表示颗粒的粒径大小。

从图6中可以较为清楚地看到，颗粒群在进入分级区后，在转子转动形成的涡流作用下，较细的颗粒受到的离心力小于气体曳力，在气流拖拽作用下，大部分细颗粒能通过导风叶片与转子叶片之间的环形区域，进入内部完成分级，而粗颗粒受到的气体曳力小于离心力，在环形区域被甩向转子外围，由于碰撞到导风叶片内壁或壳体，失去动量，无法完成分级。此外，在颗粒运动后期，转子内部依然可以一些粒径较大的颗粒，证明颗粒的分级的确是一个概率事件，在分级过程中，细颗粒完成分级的概率较大而粗颗粒通过分级的概率较小。因此通过理论计算的分级粒径只能表征该粒径的颗粒进入粗粉和细粉的概率相等，各为50%，在此基础上，粒径增大，进入粗粉的概率增大，而进入细粉的概率减小。

图6 不同粒径颗粒群在分级区实时运动

3 结 论

（1）对颗粒进行受力分析，得到了颗粒粒径对颗粒分级过程中受力的影响，对颗粒在分级区内的运动特性作出定性判断。在理论分析基础上，对颗粒在选粉机分级区内运动特性分别进行了稳态和非稳态数值模拟。

（2）在稳态模拟中考察了不同颗粒在分级区内的运动轨迹和分级效率，结果表明，颗粒在分级区内分级过程是概率事件，理论计算得到的分级粒径表示该粒径颗粒进入粗粉和细粉的概率相等。在非稳态模拟中对颗粒运动进行实时跟踪，得到了颗粒运动随时间变化的规律，再现了颗粒在分级过程中的运动过程。

（3）通过理论分析和数值模拟得出，颗粒在选粉机内的分级过程是一个概率事件，粒径较小的颗粒进入细粉的概率大，进入粗粉的概率小，而粒径较大的颗粒进入细粉的概率小，进入粗粉的概率大。研究结果为选粉机结构改造和操作参数优化提供了模拟方法和数据基础。

[1]王劲，郭天德.分级技术在中草药超细粉碎生产中的应用[J].中国粉体技术，2008（1）：36-38.

[2]陆厚根.粉体工程概论[M].上海：同济大学出版社，1993：68-69.

[3]李洪，李双跃，刘继光.干式空气分级机分类与设计概论[J].建材发展导向，2006（2）：62-66.

[4]杜妍辰，王树林.颗粒在涡轮式分级机分级轮中的运动轨迹[J].化工学报，2005，56（5）：824-828.

[5]王仲春，曾荣，李素荣.高效笼式选粉机的选型计算[J].水泥技术，2006（3）：25-29.

[6]黎国华，聂文平.涡轮分级机内腔流场的数值仿真研究[J].武汉理工大学学报，2004，26（5）：71-73.

[7]綦海军，李双跃，李翔，等.立磨选粉机操作参数对分级流场影响的数值模拟[J].中国粉体术，2012（2）：12-16.

[8]Marticorena B，Bergametti G.Modeling the atmospheric dust cycle：1.Design of a soil derived dust emission scheme [J].Geophys Res.，1995，100 （ 8 ）：16415-16430.

[9]Marticorena B，Bergametti G，Aumont B，et al.Model-ing the atmospheric dust cycle：2.Simulation of Saharan dust sources[J].Geophys Res.，1997，102（4）：4387-4404.

[10]赖志强，张承中，高建华，等.半干旱农田地区DPM模型适用性初步研究[J].水土保持通报，2011，31（3）：123-126.

[11]赵立新，崔福义，蒋明虎，等.基于雷诺应力模型的脱油旋流器流场特性研究[J].化学工程，2007，35（5）：32-35.