湍流状态下单组分气液相平衡体系压力的变化

张珍禛，姚 远，罗会娟，宋俊男，江小波，郭 锴

（1北京化工大学化学工程学院，北京 100029；2中国石油天然气股份有限公司石油化工研究院，北京 100195）

纯液体与其气相在一定温度下可达到一个动态平衡状态，这个状态被定义为单组分气液相平衡[1]。气液相平衡现象广泛地存在于化工生产过程和日常生活中，如精馏、远距离液体输送和液体空化等。这些过程中常常涉及流动和体系压力的变化。许多学者就这些现象做了大量的研究工作[2-4]。大部分研究者认为，流体流动引起了流体局部温度和压力的变化，导致局部液相汽化，从而引起体系压力的变化[5-6]。文献中可以查到许多计算液相主体中局部压力和相变化的数学模型[7-8]。但是，这些模型中都没有提及体系的相平衡是否会受到流体流动的影响。因此，传统的计算模型在对实际情况的计算中常常表现出其局限性，计算结果常与实际工况出现偏差。关于流体流动对气液相平衡体系压力变化的影响的研究，在化工实践应用和对传统计算模型的完善方面都有十分积极的意义。

本文研究的对象为单组分气液相平衡体系的压力，静态情况下也被称为液体饱和蒸汽压。目前最公认的计算饱和蒸汽压的方法是安托尼方程[1]。安托尼方程经过几十年的研究与发展，已从最初的三参数方程渐渐演变成改良的三参数方程、五参数方程和多参数方程，计算的精度也较先前有了大大的提高[9]。安托尼方程是基于实验结果的经验方程，实验过程中液体不可避免地会发生流动，这就导致了使用安托尼方程解释流动液相主体中的相变化时的不准确。在长距离油品运输中，运输管路内压力的变化、潜艇航行时空化区的压力等很难准确地估计，十分容易引发危险。因此，研究流动对单组分体系气液相平衡体系压力变化的影响有十分广泛的应用。

本研究选用了 6种不同的纯液体作为研究对象，包括水、乙醇、正丙醇、异丙醇、乙酸和丙酮，在不同的温度和湍动程度下进行实验。为了覆盖更广的物性和流动范围，每个物系都在8个不同温度和14个不同流速下进行实验。实验数据使用在线采集系统采集，基于实验数据和传统理论，提出了关于动态体系压力、物性、温度和流动速度的新的经验方程。

1 实验部分

图1是本研究中的实验流程图。基本的实验设备是一台DHG-90055A型恒温水浴振荡床，可以一定的速度做水平圆周运动。该振荡床的操作温度范围为 0～100 ℃，可控制的最小温差为 0.5 ℃；转速控制范围为0～210 r/min，可控制的最小转速为10 r/min。在恒温振荡床上固定有一定制的密封罐，密封罐顶部连接有一个压力传感器和一个温度传感器。该密封罐气密性良好，换热良好。顶部的压力传感器工作范围为0～35 kPa，最小测量精度为10 Pa；温度传感器工作范围为 0～200 ℃，最小测量精度为 0.01 ℃。压力和温度传感器都通过一台（XSDAL-HIIIIB1s2V0型）数模转换器连接在计算机上。在线采集设备每1 s记录一次系统压力和温度数据。

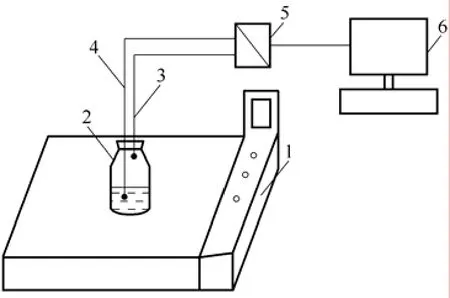
图1 实验流程图

实验开始前，将实验用的纯液体加热煮沸除去溶解的气体。液体沸腾一段时间后，将沸腾的液体移入密封罐中，将恒温水浴振荡床设定到实验温度，并用真空泵抽去密封罐中液体上方气体，观察压力和温度传感器数值，使体系压力维持在该温度下液体饱和蒸汽压，以保证实验体系达到了实验温度下的静态气液相平衡状态。

2 结果与讨论

2.1 动态平衡体系压力

为探讨流动时相平衡体系的压力变化规律，将实验的6个不同物系分别在相同的温度和振荡频率下进行实验，观察不同体系间的变化规律是否有共同点。图2为6种纯液体流动时相平衡体系压力的变化与时间的关系。

图2 不同物系在298.15 K、150 r/min时体系压力随时间的变化

从图2中可以观察到，不同的物系的压力随着时间的变化呈现相似的规律。系统压力变化都从零开始逐渐变大，然后趋于一个稳定值，从实验开始到压力达到稳定，一般都在60 s以内。为便于研究，将稳定时的系统压力定义为动态平衡压力。不同体系的动态平衡压力与相平衡压力的差值之间并没有明显的规律，从图2可说明，动态平衡的现象在不同的物系中是普遍存在的，但动态平衡的压力与物性和温度间的关系还需要进一步的研究。

热力学中提及的饱和蒸汽压是一个状态量，其数值只与物质的种类和温度有关，与流体体积无关。为研究动态平衡压力是否可以与饱和蒸汽压进行类比，对同一物系、不同的处理体积，在相同的实验条件下进行了重复实验。其中，水的实验结果列在表1中为例。

表1 不同体积的水在相同实验条件下的动态平衡压力变化

从表1可以看出，对于相同的物系，在同样的实验条件下，液体体积对体系动态平衡压力的数值无影响。由此，可以将动态平衡压力与液体饱和蒸汽压进行类比。动态平衡压力广泛存在于流动的液体中，且仅与液体的物性、温度和湍动程度有关。

由于不同的液体在相同的温度下蒸汽压不同，单个体系的压力变化又很难表达动态平衡压力的变化规律，因此引进了一个新的参考量，即动态平衡压力偏移率R，见式（1）。

动态平衡压力偏移率是动态平衡压力与饱和蒸汽压的差值占饱和蒸汽压的比例。不同液体的饱和蒸汽压选用五参数的安托尼方程计算，如式（2）。

式（2）中不同物系的安托尼方程参数在表 2中给出[10]。为了分别考察物性、湍动程度和温度对动态平衡偏移率的影响，选择3个特殊的物系进行对比。液体的湍动程度通常用雷诺数Re来表征。当液体体积、振荡频率和容器大小形状一定时，Re仅与液体物性有关。另一方面，相平衡的温度是该压力下液体的泡点温度（Tb），而液体泡点温度的极限是临界温度（Tc）。雷诺数和临界温度可以作为物性和湍动程度对动态平衡偏移率影响的两个重要考察因素。正丙醇和异丙醇具有相同的密度和黏度，而两物系的临界温度不同。当液体量、振荡频率和温度都相同时，正丙醇和异丙醇体系的雷诺数是相同的。于是，选择正丙醇和异丙醇体系进行对比实验，考察不同临界温度对动态平衡偏移率的影响。丙酮和异丙醇体系具有不同的黏度和密度，但两物系的临界温度相同，对这两个物系的对比实验，可以考察不同湍动程度对动态平衡偏移率的影响。

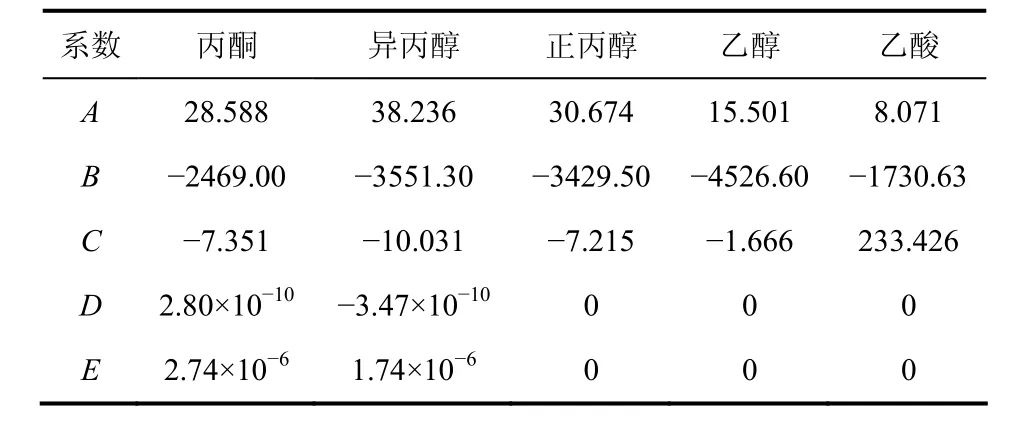
表2 安托尼方程系数

2.2 物性相同时，R与振荡速度和实验温度的关系

图3是正丙醇和异丙醇体系在振荡频率分别为110 r/min、150 r/min和190 r/min时R随实验温度的变化。从图3中可以看出，对单独的物系，在振荡程度一定时，偏移率随着实验温度的升高而增大。在实验温度一定时，偏移率随着振荡频率的增大而增大。也就是说，温度越高，振荡频率越高，动态平衡偏移的现象就越明显。正丙醇的临界温度为536.7 K，异丙醇的临界温度为508.1 K。图3中显示，在相同的实验条件下，正丙醇的实验点都落在异丙醇的下方，说明湍动程度一定时，临界温度越高的体系其动态平衡的偏移率越小。

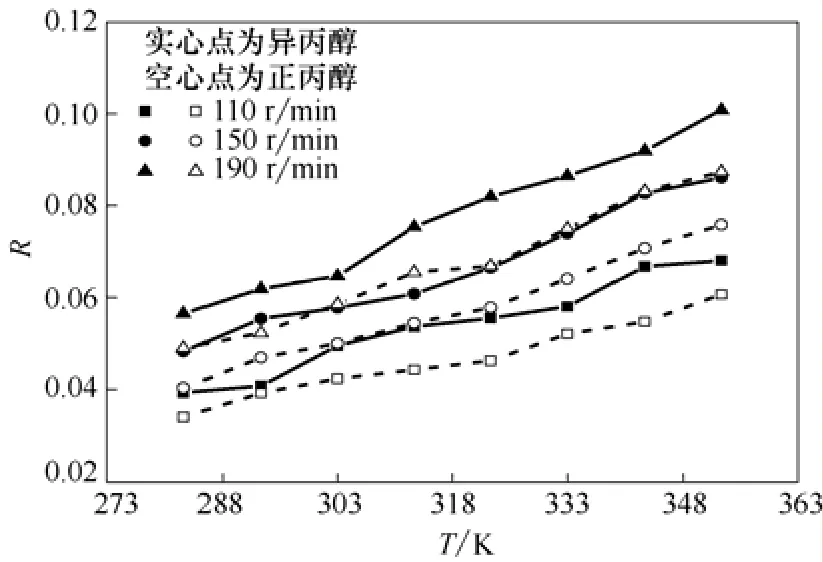
图3 正丙醇、异丙醇在不同振荡频率下R随温度的变化

2.3 临界温度相同时，R与振荡速度和实验温度的关系

图4是丙酮和异丙醇体系在振荡频率分别为110 r/min、150 r/min和190 r/min时R随实验温度的变化。从图4中可以看出，对于单一物系，R随温度和振荡频率的变化与图3中呈现相同的规律。这两个物系有相同的临界温度，为比较湍动程度对实验结果的影响，首先比较了不同物系在实验条件下的雷诺数。

雷诺数通过式（3）计算。

式（3）中，直径d为实验容器的特征直径，其数值为7.46×10−2m。实验过程中，实验容器进行匀速水平圆周运动，将圆周运动的切线速度当作液体流动速度，进行雷诺数的计算。不同物系在303.15 K时的雷诺数数据在表3中给出。

根据表3的数据可知，当液体体积、振荡频率和实验容器一定时，实验范围内丙酮体系的雷诺数远大于异丙酮体系。图4中，相同实验条件下丙酮的实验点都高于异丙醇，说明当实验条件和体系临界温度都确定时，液体的湍动越剧烈动态平衡的偏移率就越大。

2.4 R与对比温度和雷诺数的关联式

为了建立实验温度与液体临界温度间的关系，引入了对比温度，如式（4）。

图4 异丙醇、丙酮在不同振荡频率下R随温度的变化

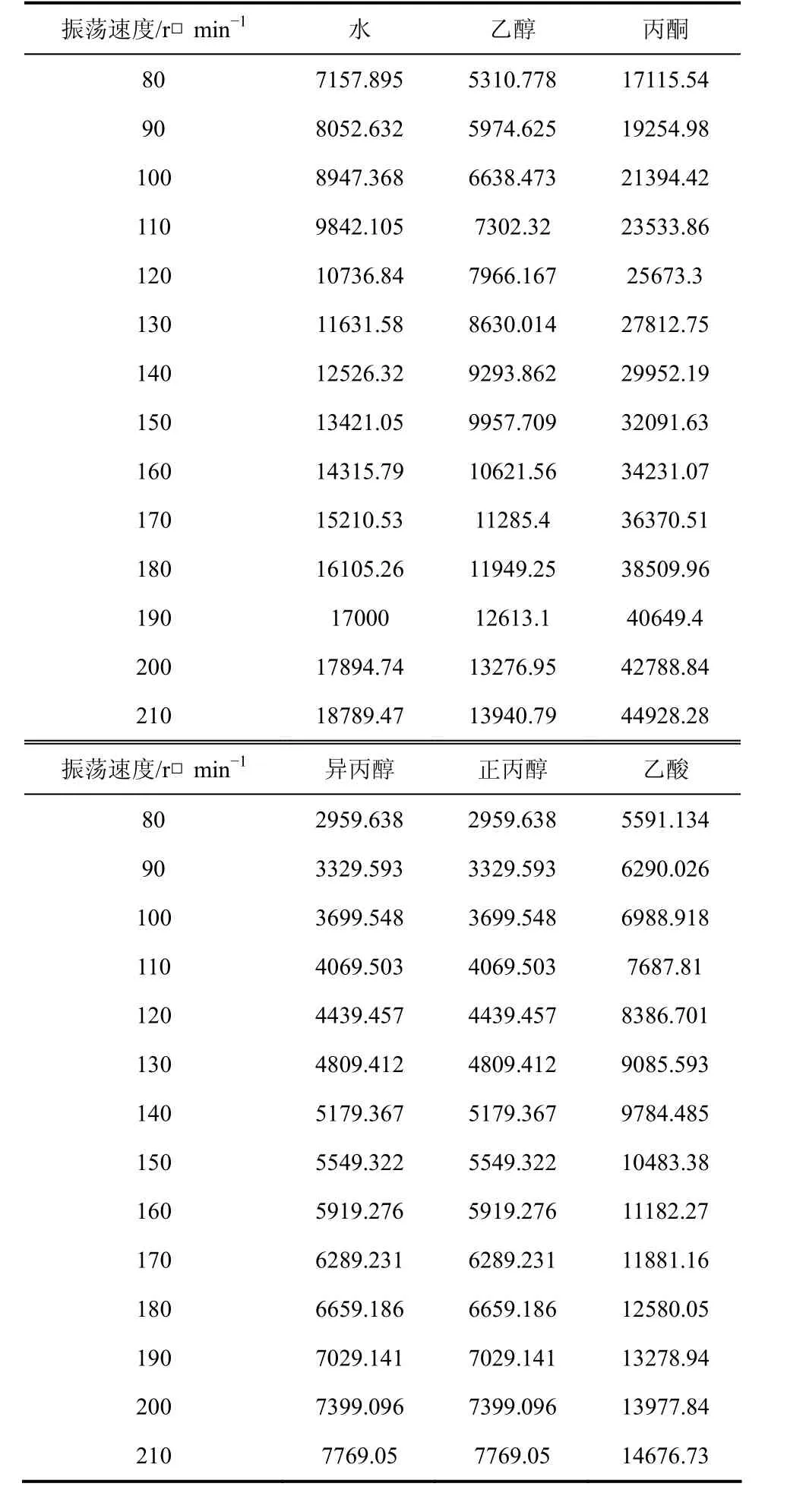
表3 不同物系在303.15 K时的振荡速度与雷诺数

将实验的振荡频率换算成雷诺数，实验温度与临界温度联系成对比温度后发现，当实验体系的雷诺数和对比温度一定时，R的数值一定，与物系无关。由此可以推断，动态平衡与静态平衡的偏移现象在纯液体中普遍存在，且偏移率是且仅是雷诺数和对比温度的函数。

为了通过实验结果拟合出R、Re和Tr的数值关系。选择6个物系，在8个温度和14个振荡频率下进行实验。实验温度从10 ℃到80 ℃，每隔10 ℃选取一个；振荡速度从80 r/min到210 r/min，每隔10 r/min选取一个，所有的实验点都在图5中给出。

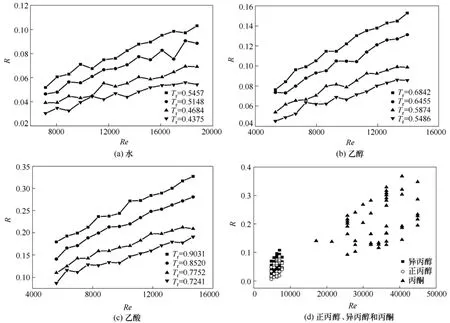
图5 6种液体在不同对比温度下R随雷诺数的变化

图5是所有实验物系在不同对比温度下R随雷诺数的变化。从图5中可以观察到，水、乙醇和乙酸的变化规律与前文描述的正丙醇、异丙醇和丙酮体系的规律一致。图5(a)中雷诺数的范围为7000～19 000，对比温度范围为 0.4375～0.5457；图 5(b)中雷诺数的范围为5000～14 000，对比温度范围为0.5486～0.6842；图 5(c)中雷诺数范围为 5000～15 000，对比温度范围为0.7241～0.9031；图5(d)中正丙醇和异丙醇在相同实验条件下有相同的雷诺数，其范围为 4000～8000，丙酮的雷诺数范围为 17 000～45 000。异丙醇和丙酮在相同实验温度下有相同的对比温度，其范围为 0.5574～0.6951，正丙醇的对比温度范围为 0.5277～0.6581。所有实验数据覆盖的雷诺数范围为4000～45 000，对比温度范围为0.4375～0.9031。

实验涉及了6个物系、8个温度和14个振荡频率。为保证所有的实验结果都是在湍流状态下得到的，只有当雷诺数大于4000的数据被用于进一步的数据拟合。基于前面的研究，动态平衡的体系压力与饱和蒸汽压的偏移率只是雷诺数和对比温度的函数。对所有实验数据进行拟合后得到关系式（5）。

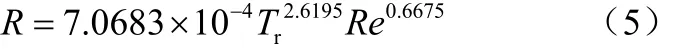
通过拟合范围可知，式（5）的适用范围为4000＜Re＜45000 且 0.4375 ＜Tr＜0.9031。

为了更清晰地表达R、Re和Tr的关系，给出它们的三维关系图（图6）。

如图6所示，在雷诺数较大时，随着对比温度的升高，R增加得更快。同样地，在对比温度较高时，随着雷诺数的增加，R增加得更快。在实验条件下，R最大可达到0.7420，最小可达0.02058。图6中同样可以观察到，当雷诺数较小时，流动对气液相平衡体系压力的影响也相对较小，也可以解释在流动并不剧烈的情况下，静态热力学的理论误差较小。同样可以预测，较剧烈的湍动程度对动态平衡的压力影响也十分明显，当湍动程度足够剧烈时，液相的动态饱和蒸汽压可达静态数值的两倍以上。

图6 R、雷诺数和对比温度的三维关系图

3 结 论

（1）对于单组分气液相平衡物系，动态压力偏移率在湍动程度相同时，随着实验温度的升高而增大；在实验温度相同时，随着湍动程度的加剧而增大。对于不同物系、相同实验条件下，临界温度越高的体系，其动态平衡偏移率越小；临界温度和实验温度相同时，湍动越剧烈的，动态平衡偏移率越大。

（2）动态平衡偏移率仅是雷诺数和对比温度的函数，与物系无关。关系式满足R=7.0683×10−4Tr2.6195Re0.6675。关系式的适用范围为 4000 ＜Re＜45000 且 0.4375 ＜Tr＜ 0.9031。

（3）雷诺数较大时，随着对比温度的升高，动态平衡偏移率增加得更快。同样地，在对比温度较高时，随着雷诺数的增加，动态平衡偏移率增加得更快。在实验条件下，动态平衡偏移率最大可达到0.7420，最小可达0.02058。

符 号 说 明

A，B，C，D，E——安托尼方程系数

d——设备特征尺寸，m

Ps——相平衡体系压力，Pa

Psd——动态平衡体系压力，Pa

△P——体系压力变化，Pa

R——动态体系压力偏移率

Re——雷诺数

T——实验温度，K

Tc——液相的临界温度，K

Tr——实验对比温度

u——液相流速，m/s

μ——液相黏度，Pa·s

ρ——液相密度，kg/m3

[1]郑丹星.流体与过程热力学[M].北京：化学工业出版社，2005：16.

[2]Tilman Knorr，Eberhard Aust，Karl-Heinz Jacob.Calculation of vapor-liquid equilibrium data of binary mixtures using vapor pressure data[J].Chemical Engineering & Technology，2010，33：2089-2094.

[3]Humpherys R A，Kroon J R.Computer modeling as a tool for selecting appropriate air valves for pipeline surge protection，In：Water resources planning and management and urban water resources[C]//New York：ASCE，1991：939-943.

[4]赵飞.混流式水轮机空化流动特性分析[J].西华大学学报：自然科学版，2012，31（2）：69-72.

[5]Stephan Scholl，Martin Schachtl，Werner Sievers，et al.Calculation methods for multicomponent adsorption equilibria[J].Chemical Engineering & Technology，1991，14：311-324.

[6]Martínez-Palou R，de L Mosqueira M，Zapata-Rendón B，et al.Transportation of heavy and extra-heavy crude oil by pipeline：A review[J].Journal of Petrol.Science Engineering，2011，75：274-282.

[7]Anciger D.水泵水轮机旋转失速与初生空化的预测[J].国外大电机，2012，73（1）：63-66.

[8]朱坤，沃恒洲，徐玉福，等.流体物性对空化气泡溃灭过程影响研究[J].合肥工业大学学报：自然科学版，2011，34（9）：1295-1297.

[9]卢焕章.石油化工基础数据手册[M].北京：化学工业出版社，1984.

[10]Carl Yaws L.Chemical Properties Handbook：Physical，Thermodynamic，Environmental，Transport，Safety，and Health Related Properties for Organic and Inorganic Chemicals[M].New York：McGraw-Hill，1998.