基于MATLAB 的电力系统稳态仿真分析

李丽霞，李 凯，路 静，姚兴佳

(1.沈阳工程学院自动控制工程系，沈阳110136;2.沈阳工业大学风能技术研究所，沈阳110023;3.沈阳晟昱咨询有限公司，沈阳110168)

电力系统稳定运行的第一道防线是电力系统暂态功角稳定控制.电力系统发生短路故障时，暂态稳定性会受到干扰，提高电力系统暂态稳定性的方法很多，由于电力是国名经济的支柱和命脉，实际考核电力系统稳定性将对经济和人身安全带来损失.因此，这里利用MATLAB 的动态仿真软件Simulink 搭建了含发电机、变压器、输电线路等的单机－无穷大系统仿真模型，对短路故障时所采取的不同措施的结果进行了仿真.

1 电力系统的暂态稳定性

电力系统暂态稳定性是指电力系统受到大扰动后，各同步发电机保持同步运行并过渡到新的运行状态或恢复到初始运行状态的能力.

引起大扰动的原因主要包括:①发生短路故障;②切除或投入系统的主要元件，如发电机，变压器以及线路;③负荷的突然变化，如大用户的投入.

其中发生短路故障的危害最大，单相短路接地占大多数，约为65%，而三相短路的几率虽然小，但是后果最为严重，短路的特征是故障点电压降低.短路对电力系统的正常运行和电气设备的危害很大，短路电流可达几万甚至几十万安培，产生热效应和电动力冲击.分析电路暂态现象时，可建立电流电压微分方程，并按初始来求解.对于稳态一般用快速而准确的ode45 函数，对于暂态用ode23 函数.

2 基于MATLAB 的单机无穷大系统模型

电力系统运行稳定分析中，常应用的系统是单机—无穷大系统，即功率无穷大，频率恒定，电压恒定，如图1 所示.单机—无穷大系统.同时也是工程上常采用的，也是电力系统仿真模拟最基本、最简单的运行方式.对实际系统近似处理，用来简化模型，方便得出结论，有利于计算过程的简化.单机—无穷大系统是具有一定代表性的，主要基于以下2 点考虑:①复杂系统都可以通过等值的第复方法归结到这一模型或者双机系统上来;②可以大大降低动态数字仿真的运算量，提高仿真速度，并很好地满足继电保护测试要求.

图1 单机－无穷大系统

应用MATLAB 中的Simulink 软件可以用图形建立仿真模型，直接用Simulink 环境中的菜单启动仿真过程，结果就显示在示波器上.Simulink 中能对调节器的参数进行调整，得到很清晰的仿真结果.目前我国以三相短路作为考查电力系统暂态稳定扰动的方式之一.因此仿真过程中设置短路故障为主要的故障方式.图2 应用MATLAB 电力系统单机－无穷大系统仿真模型.

图2 SPS 单机－无穷大系统仿真模型

3 单机－无穷大系统仿真模型参数设置

3.1 图中各模块参数设置

三相电源:无穷大系统采用三相电源模块代替，参数设置为230 kV，100 GVA，A 相相角为0°，X/R =10.三相短路器使用默认参数. 输电线路选择分布参数模型，每回参数设置为R1= 0.038 42 hms /km，R0=0.220 19 hms /km，L1=1.037 8e－3 H/km，L0=2.839 4e－3H/km，C1=11.2584e－9 F/km，C0=8.157e－9 F/km，220 kV，110 km，极限传输容量为350 MW.三相变压器参数设置为900 MVA，50 Hz，Delta(D1)/Yg 接线，20 /230 kV，R1=R2=1e－6(p.u.)，L1=0(p.u.)，L2=0.15(p. u.)，Rm=Lm=500(p. u.)，其中p. u. 表示单位是标幺值.三相负载RLC 并联:P =1 W，QL=1 Var，QC=1 Var.励磁系统使用默认参数. 同步发电机的参数设置为round(隐极机)，900 MVA，20 kV，50 Hz，xd=1.8，xd' =0.3，xd″=0.25，xq=1.7，xq' =0.55，xq″=0.25，xl=0.2，Rs=0.002 5，Td0'=8 s，Td0″=0.03 s，Tq0'=0.4 s，Tq0″=0.05 s，H=6.5 s，p=4.各电抗、电阻均为标幺值(p.u.).通用电力系统稳定器使用默认参.Vref 常量设置为1.Pmec(pu)常量设置为0.5374.复合测量模块设置为选择vs－qd;d－theta;dw. Gain设置为60/2/Pi. Powergui 模块:双击POwergui;单击Configure parameters:将Simlation type 选择为phasor，潮流计算方式频率改为50 Hz.

4 各种提高暂态稳定性措施的运行效果仿真

系统受到大的扰动后发电机机械功率和电磁功率的差额(即加速功率Pm－ Pe)是导致系统暂态稳定破坏的主要原因，因此减少大扰动后发电机的加速功率是首先考虑的措施［4］.在图2 中，没有采取有效措施来提高系统的暂态稳定，在此情况下系统受到大的扰动后很容易失去平衡. 现在图2 的基础上采取一些有效措施，包括使用电力系统稳定器，附加故障限流器等，并在这些措施的基础上进行仿真运行.由于引起系统不稳定的大扰动中，短路故障最常见，危害也最大，因此在线路L2 出口处设置各种短路故障作为对系统的大扰动，短路故障发生时间均定在1 s.

在动态仿真时设置下列情况:

1)在线路L2 出口处设置三相接地短路故障，1.1 s时将故障切除，通过投入和退出PSS 来分析使用电力系统稳定器PSS 对提高系统暂态稳定性的效果.如图3、图4 所示.

2)在线路L2 出口处设置三相接地短路故障，1.4 s时将故障切除，仿真时投入PSS，将此仿真结果与1)中1.1 s 时切除故障的仿真结果进行比较，对快速切除故障的效果进行分析.如图5 所示.

3)在线路L2 出口处设置三相接地短路故障，1.4 s时将故障切除，仿真时附加故障限流器(FCL)并投入PSS，对比图2 来分析采用FCL 对于提高系统暂态稳定性的效果.如图6 所示.

图3 三相接地短路(1.1 s 切除故障，仿真不投PSS)

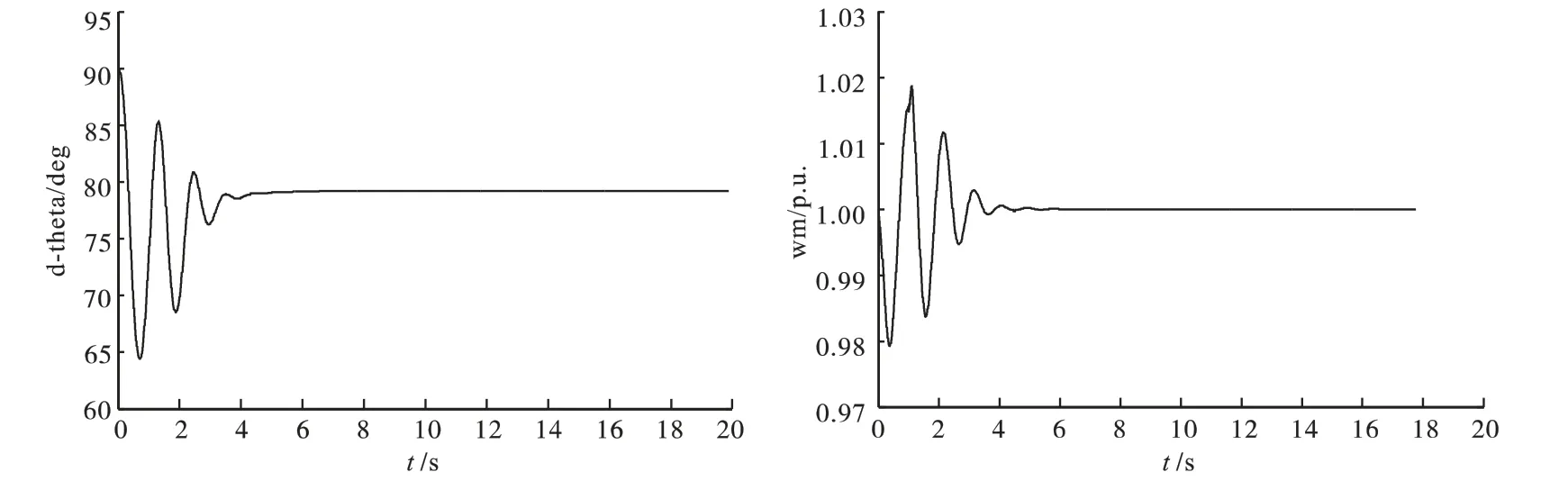
图4 三相接地短路(1.1 s 切除故障，仿真附加PSS)

图5 三相接地短路(1.4 s 切除故障，仿真附加PSS)

图6 三相接地短路(1.4 s 切除故障，仿真附加FCL 同时投PSS)

图3 系统附加PSS，三相接地短路1.1 s 时切除故障，系统4 s 时趋于稳定，图4 系统未投入PSS，尽管采取了快速切除故障的措施，但系统直到16 s 时才趋于稳定.将图3 与图4 的仿真结果作对比，可见在系统中使用电力系统稳定器(PSS)可有效增加系统的阻尼，使系统快速趋于稳定. 因此使用PSS 是提高电力系统稳定性的有力措施.

图5 系统附加PSS，三相接地短路1.4 s 时切除故障，系统失去了稳定性.比较图5 慢切除故障和图4 快速切除故障的系统运行稳定性，可见快速切除故障是保证系统暂态稳定性的有效措施.

图6 系统附加PSS，并在线路首端装设故障限流器FCL，三相接地短路1.4 s 时切除故障，系统4 s 时趋于稳定.将图6 与图5 的仿真结果作对比，可见装设故障限流器(FCL)，可快速限制短路电流，即使采取慢切除故障措施，系统仍能保持暂态稳定性.因此装设故障限流器(FCL)也可有效地提高电力系统暂态稳定性.

5 结 论

通过单机－大系统对单力系统暂态稳定领域的故障判断与分析，以MATLAB Simulink 仿真系统为依托，非常容易的建立了电力系统的各个组成部分，联接成了电力系统的模型，最终建立了系统仿真的模型.通过模型模拟了一些故障，并对这些故障进行的检测与分析，最终解决了故障，通过对故障的分析验证了方法的正确性与准确性，利用MATLAB Simulink 系统为电力系统仿真提供了更加准确与方便的办法. 结果表明，MATLAB SPS 具有强大地仿真功能，利用MATLAB 进行电力系统仿真准确率高，而且没有风险，通过精准的计算，大大的提高了精度，是分析电力系统的有力工具.

［1］张少如，李志军，吴永俭，等.Matlab 与电力系统仿真［J］.河北工业大学学报，2005，34(6):5－9.

［2］何仰赞，温增银.电力系统分析:3 版［M］.武汉:华中科技大学出版社，2002.(5):95－96.

［3］姚李孝，姚金雄，安 源. 基于Matlab/Simulink 的高压输电线路故障定位的仿真研究［J］.电网技术，2005，(5).

［4］吴明强，李霁红，曹爱东，等.故障诊断专家系统综合智能推理技术研究［J］. 计算机测量与控制，2004，12(10):932－934.

［5］周荣光，电力系统故障分析［M］.北京:清华大学出版社，1988.(1):2－3.

［6］赵彩宏，田立军，邹贵彬，等.FCL 对电力系统暂态稳定性影响的机理分析与仿真［J］. 电力自动化设备，2001，21(2):14－17.

［7］李维波.Matlab 在电气工程中的应用［M］. 北京:中国电力出版社，2007.(7):342－343.

［8］李光琦.电力系统暂态分析:2 版［M］.北京:水利电力出版社，1995.

［9］常 勇，王 莹，李立新. 电力系统暂态稳定方法综述［J］.云南电力技术，2009.

［10］盛义发，邓国扬，王浩宇，等.同步发电机新型励磁系统的研究［J］.南华大学学报，2003(1):1－6.

［11］张 森，张正亮. Matlab 仿真技术主导实例应用教程［M］.北京:机械工业出版社，2004.

［12］张葛祥，李 娜.Matlab 仿真技术与应用教程［M］.北京:国防工业出版社，2004.

［13］蔡克红，李 升.电力系统暂太稳定性仿真:基于Matlab/Simulink［J］.江西电力，2006.

［14］Warut Suampun，Hsiao－Dong Chiang.Critical Evaluation of Methods for Estimating Stability Boundary for Transient Stability Analysis in Power Systems［J］.Power and Energy Society General Meeting，2010.

［15］Elgerd O I.Electric Energy System Theory－An Introduction［J］.McGraw－Hill Book Co，1982(4):61－66.

［16］ZMhong Ye，D Boroyevich，Fred C Lee.Modeling and control of zero－sequence currents in parallel multi－phase converters［C］.IEEE Power Electronics Specialists Conference Galway，2000:1549－1556.

［18］ Kundur P. Power System Stabiliby and Control［J］.Mcgraw－Hill，1994(2):25－26.

［19］ Grainger J J，Stevenson W D. Power System Analysis［J］.Mcgraw－Hill，1994(4):44－47.

［20］ Venikov V A. Transient Processes in Electrical Power Systems［J］.Mir Publishers，1980(2):12－13.