提高牛顿环测平凸透镜曲率半径精度的方法对比研究

2013-07-16左安友吴胜宝

湖北民族大学学报(自然科学版) 2013年1期

左安友，吴胜宝，朱瑜

(湖北民族学院理学院，湖北恩施 445000)

牛顿环实验是大学物理实验中的光学基础实验之一，是学生深入了解光的干涉原理的基础性实验.同时牛顿环在科学研究、工业生产及检验技术中的直接运用，也使得人们一直研究其测量精度的提高.在实验改进上主要分为两类:一是实验方法上的改进［1－2］;二是实验装置的改进.笔者认为方法的改进是提高精度的关键所在.文中采用了三种不同测量方法测量同一平凸透镜的曲率半径，从而达到用光学测量手段得到曲率半径精度最高的目的.

1 牛顿环测平凸透镜曲率半径实验原理

牛顿环装置及光路示意图如图1所示.设入射光的波长为λ，第k级暗条纹对应的空气薄膜厚度为ek，考虑到下界面反射时有半波损失λ/2，当光线垂直入射时总光程差由薄膜干涉公式求得［3－4］:

n为空气的折射率，为1，根据干涉条件:

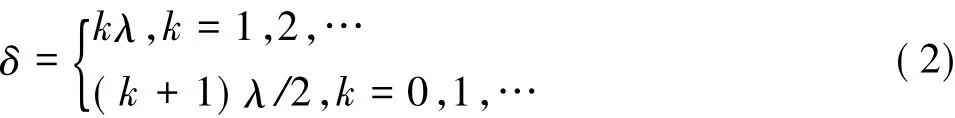
图1 牛顿环装置及光路示意图Fig.1 The schematic graph for Newton ring device and light propagation

因为R≫ek上式中的可略去不计，故:

在实验中选取暗环作为测量对象，以rk表示第k个暗环的半径，rk+m表示第k+m个暗环的半径，有:=两式相减，得:

式中:Dk+m，Dk是k+m级与k级牛顿环的直径.

2 研究使用的基本方法简介

2.1 数据测量方法介绍

1)叉丝竖线切环法［5］:调节叉丝竖线竖直(人为判断)，调节叉丝交点与牛顿环中心重合(人为判断)，这样测量的Dk+m、Dk才近似为牛顿环的直径.对每一环的测量时，左边取叉丝竖线与环外切时读取并记录数据，右边取叉丝竖线与环内截时读取并记录数据.

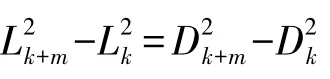
3)叉丝交点对准法二:只调节叉丝交点接近牛顿环中心，无需调节叉丝竖线竖直.测量时叉丝交点对准待测干涉暗环条纹宽度中心，读取并记录左右侧数据l左、l右，两者作差(l右－l左)得到弦长L，然后运用公式(5)进行计算，得到曲率半径R.

2.2 误差理论及数据处理方法

1)误差理论［7－10］:采用牛顿环测平凸透镜的曲率半径是一种间接测量方法，根据误差传递理论，R的相对不确定度为:

B类分量:这一类分量主要反映非随机误差的影响，对于本实验可认为这类不确定度主要由读数显微镜仪器误差［11－12］产生，表示为:

本文中Δ仪的值［13］取为:0.004 mm，由于直径D由测量值d左、d右计算得出:D=d右－d左由此得到:

由误差传递公式可得:

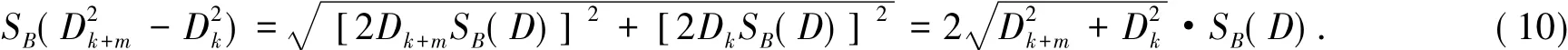
由上式可以看到D2－D2的B类分量随着测量值的变化而变化.

k+mk

合成不确定为:

2.2.2 λ的不确定度.由于钠光灯的波长为λ=(589.3±0.3)nm，就可以得λ的不确定度为:

透镜曲率半径为:

y(k)的不确定度为:

R的相对不确定度为:

平凸透镜曲率半径最终表示为:

3 实验操作流程

R的不确定度为:

1)调节牛顿环仪装置上的三个调节螺丝:螺丝不能拧得过紧也不能过松，可采用类似调节分光计的各半调节法，通过观察调到牛顿环中心暗斑为最小又不松动最佳.

2)将牛顿环仪置于读数显微镜的载物台上，调节读数显微镜目镜使分划板十字叉丝最清晰.再调节显微镜筒找到清晰的干涉圆环.移动牛顿环仪，让叉丝交点尽可能对准牛顿环干涉中心，并调整光源使整个视场清晰且明暗环对比度最好.

3)调节测微鼓轮向左移动读数显微镜筒，使视场中的叉丝交点由中心向右移动到待测最大级干涉暗环的下一级附近，再反转测微鼓轮使显微镜筒一直向右缓慢移动，使叉丝竖线分别与各待测干涉暗环相切(左侧外切，右侧内截)，记录下对应的左右读数d左、d右.另外两种测量方法按照方法介绍中的操作进行.

4)计算出D=d右－d左，再由式(4)即可求得平凸透镜的曲率半径.另外两种方法采用式(5)计算曲率半径.

4 数据采集与整理

4.1 实验数据采集

表1～表3分别为笔者采用“叉丝竖线切环法”、“叉丝交点对准法一”、“叉丝交点对准法二”测量数据记录表，为后面的数据处理和分析对比提供依据.

表1 叉丝竖线切环法实验数据记录表(mm)Tab.1 The experimental data for the method of the vertical of cross tangent to strip(mm)

表2 叉丝交点对准法一实验数据记录表(mm)Tab.2 The experimental data for the first scheme of the method of cross intersection aiming at center of strips(mm)

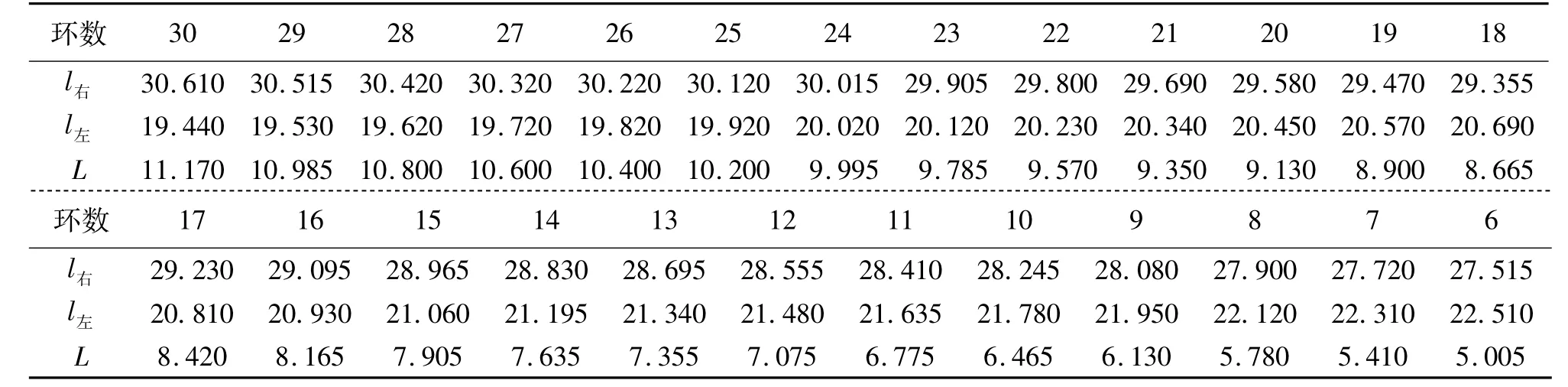
表3 叉丝交点对准法二实验数据记录表(mm)Tab.3 The experimental data for the second scheme of the method of cross intersection aiming at center of strips(mm)

4.2 数据整理与计算

4.2.1 叉丝竖线切环法实验数据整理与计算将整个实验数据分为三组(m=10)分别用逐差法和加权平均法计算曲率半径.具体如表4～6所示.

分别由式(14)、(16)得:y(k)=42.367 mm2，SC(y(k))=0.0486 mm2.

表4 取m=10，k=16～20时的数据处理表(mm)Tab.4 he experimental data for m=10，k=16 ～20(mm)

表5 取m=10，k=11～15时的数据处理表(mm)Tab.5 The experimental data for m=10，k=11 ～15(mm)

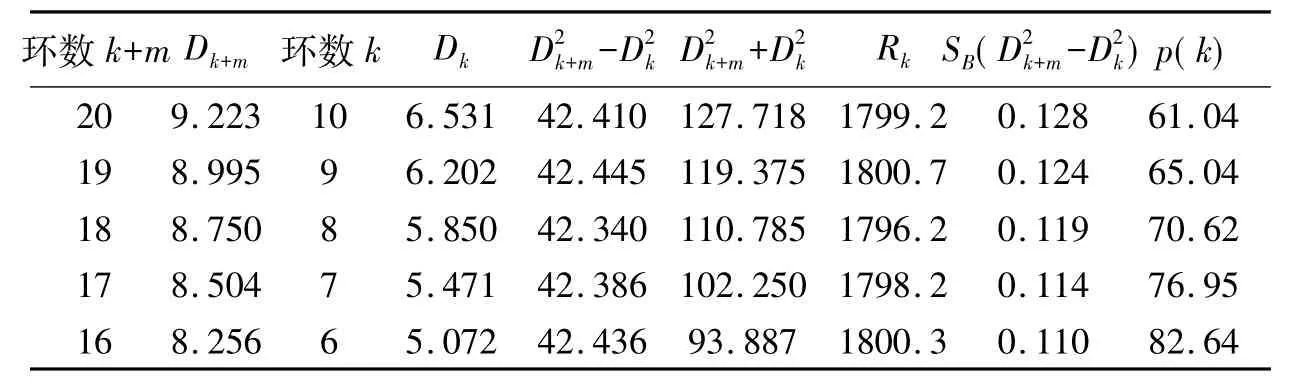
表6 取m=10，k=6～10时的数据处理表(mm)Tab.6 The experimental data for m=10，k=6 ～10(mm)

表7 取m=10，k=16～20时的数据处理表(mm)Tab.7 The experimental data for m=10，k=16 ～20(mm)

4.2.2 叉丝交点对准法一实验数据整理与计算将实验数据分为三组(m=10)采用加权平均法进行处理，具体如表7～9所示.

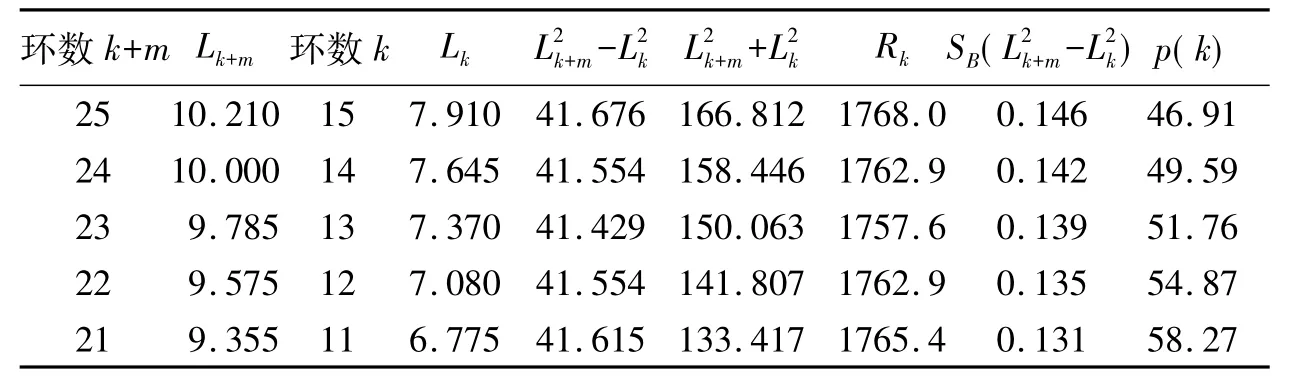
表8 取m=10，k=11～15时的数据处理表(mm)Tab.8 The experimental data for m=10，k=11 ～15(mm)

表9 取m=10，k=6～10时的数据处理表 (mm)Tab.9 The experimental data for m=10，k=6 ～10(mm)

4.2.3 叉丝交点对准法二实验数据整理与计算将实验数据分为三组(m=10)采用加权平均法进行处理，具体如表10～12所示.

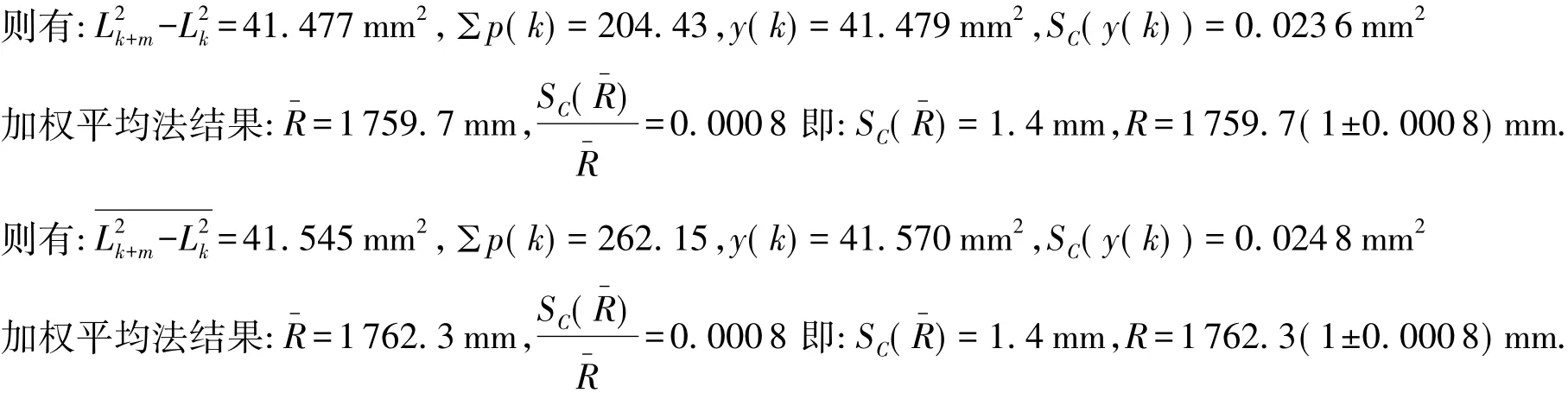
表10 取m=10，k=16～20时的=数据处理表(mm)Tab.10 The experimental data for m10，k=16 ～20(mm)

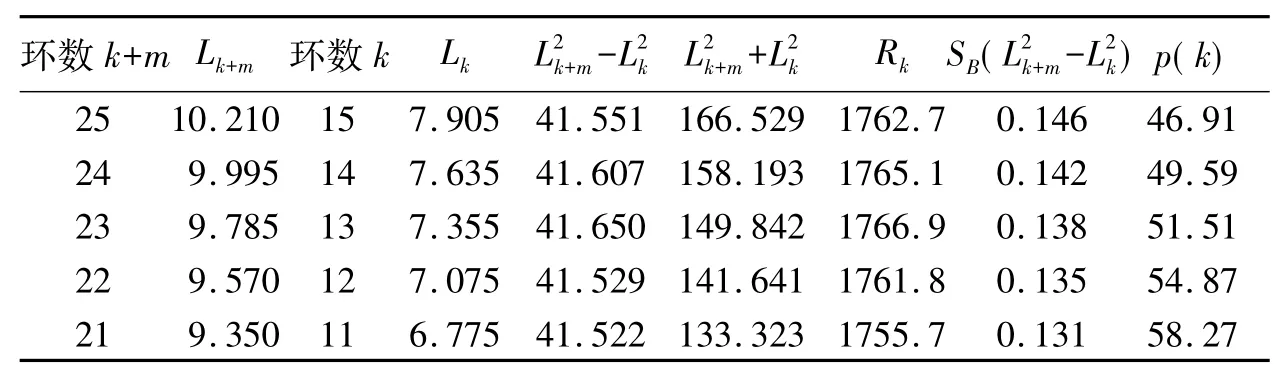
表11 取m=10，k=11～15时的数据处理表(mm)Tab.11 The experimental data for m=10，k=11 ～15(:mm)

表12 取m=10，k=6～10时的数据处理表(mm)Tab.12 The experimental data for m=10，k=6 ～10(mm)

5 计算结果分析

5.1 各个计算结果的相对不确定度及不确定度的比较

对统一采用加权平均法的处理结果进行比较(m=10).

1)叉丝竖线切环法:

第一组数据(表4):相对不确定度:0.13%;不确定度:2.3 mm

第二组数据(表5):相对不确定度:0.13%;不确定度:2.3 mm

第三组数据(表6):相对不确定度:0.07%;不确定度:1.3 mm

2)叉丝交点对准法一(叉丝竖线竖直):

第一组数据(表7):相对不确定度:0.13%;不确定度:2.3 mm

第二组数据(表8):相对不确定度:0.11%;不确定度:1.9 mm

第三组数据(表9):相对不确定度:0.15%;不确定度:2.7 mm

3)叉丝交点对准法二(叉丝竖线倾斜):

第一组数据(表10):相对不确定度:0.08%;不确定度:1.4 mm

第二组数据(表11):相对不确定度:0.08%;不确定度:1.4 mm

第三组数据(表12):相对不确定度:0.07%;不确定度:1.2 mm

通过以上比较可知:叉丝交点对准法二，即叉丝竖线倾斜时，测量结果的相对不确定度较其他两种方法小且稳定，不确定度也最小.所以叉丝交点对准法二(叉丝竖线倾斜)是三种方法之中最佳的测量方法.对此结论从理论上进行分析:叉丝竖线倾斜时人的视觉感官对叉丝交点是否对准暗条纹宽度中心更敏感，测量所得数据就更准确，从而较其它两种方法所测数据的相对不确定度小，这样结果的相对不确定度就减小了.相反，叉丝竖线竖直时反而不能准确判断暗条纹中心位置，使得结果相对不确定度偏大，从上面的结果也体现了这一点，同时还有造成测量中无意识与叉丝竖线切环法混淆的错误操作的可能.笔者认为叉丝竖线切环法相对不确定度较大的主要原因是:暗环和亮环的分界处是人眼无法准确判断的，这样就会引入较大的误差;相反，暗环最暗处人眼则更容易判断，叉丝交点对准暗环中心就更准确，所以误差对结果相对不确定度影响小.

5.2 分析暗环环数之差m对相对不确定度的影响

三种测量方法的数据处理中都是取暗环环数之差m=10.按理论分析m的取值不同，对准误差对结果的影响也应该有差异，下面取叉丝交点对准法二(叉丝竖线倾斜)的实验数据进行研究，m 分别取 5、15、20.如表 13 ～15所示.

表13 取m=5，k=11～15时的数据处理表(mm)Tab.13 The experimental data for m=5，k=11 ～15(mm)

表14 取m=15，k=11～15时的数据处理表(mm)Tab.14 The experimentaldata for m=15，k=11 ～15(mm)

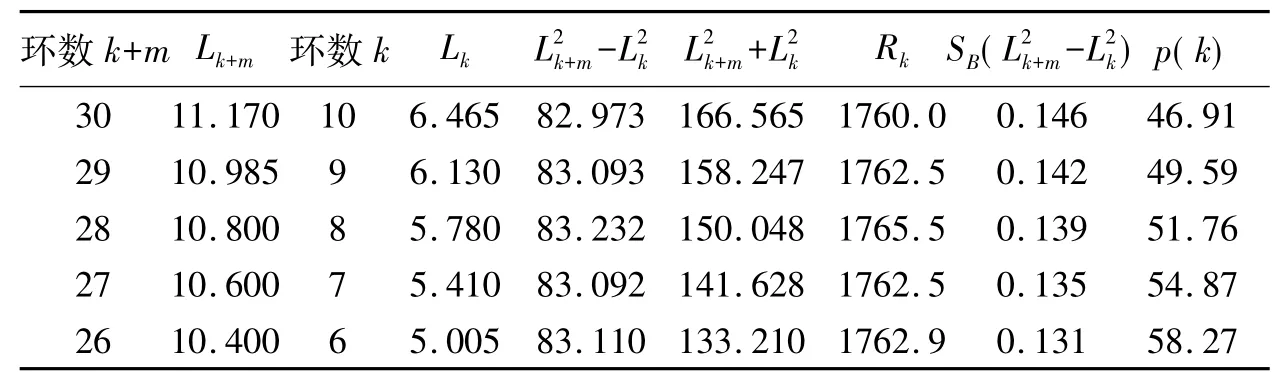
表15 取m= 20，k = 6 ～10 时的数据处理表( mm)Tab. 15 The experimental data for m= 20，k = 6 ～10 ( mm)

加权平均法结果:

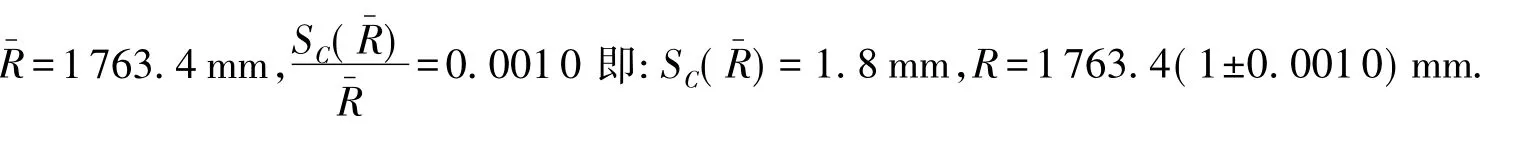
通过以上几组数据结果的相对不确定度的比较，特别是逐差法结果的相对不确定的互相比较可以看到，m=20时加权平均法和逐差法所得结果的相对不确定度最小.m的值越大相对不确定度越小，不确定度也越小，总的趋势是随着m的增大，相对不确定度减小.将上面m=15的表14的结果的相对不确定0.0010与前面计算的m=10的表11的结果的相对不确定度0.0007比较有些反常，但相差不大，个人认为是测量中某个数据不准确所致.由此可见暗环环数之差越大，其对相对不确定度的影响越小.

6 结论

本文通过逐差法、加权平均法处理叉丝竖线切环法所测得实验数据证实了加权平均法是最佳的数据处理方法.随后证明了叉丝交点对准法二(叉丝竖线倾斜)是三种测量方法中的最佳方法.本文还研究了暗环环数之差m的大小对相对不确定度的影响，考虑到实验实际:距牛顿环中心近的暗环宽度过宽，则暗环宽度中心不易判断而使测量不确定度增大;距牛顿环中心太远的暗环宽度及环间距过小，且明暗条纹对比度也愈来愈弱，从而很难确定暗环宽度中心位置使测量不确定度增大.所以m不可能无限大，为计算方便考虑，一般选用m=20较为合适，暗环级次选择6～35是比较合适的.处理数据时发现加权平均法过于复杂，而逐差法相对简单得多，并且两者在R－的大小上相差很小.所以在不要求精度很高的曲率半径测量中，逐差法任然是一种简单可行的数据处理方法.

［1］王奇思，孙健，马世红.基于彩虹光学原理测量介质材料折射率的新方法［J］.大学物理，2012(2):55－58.

［2］孔维姝，赵维金.探讨测量液体表面张力系数的优化方法［J］.大学物理，2012(3):32－34.

［3］李学慧，高峰，孙炳全，等.大学物理实验［M］.北京:高等教育出版社，2006:82－84.

［4］陈聪，李定国，刘照世，等.大学物理实验［M］.北京:国防工业出版社，2008:165－166.

［5］蒋冰峰，熊小勇，高雁军.用牛顿环测平凸透镜曲率半径的规范操作研究［J］.湖北民族学院学报:自然科学版，2004，22(4):83－85.

［6］左安友，翁祝林，李兴鳌.牛顿环实验误差分析及改进［J］.湖北民族学院学报:自然科学版，2006，24(4):410－412.

［7］李春贵.大学物理实验中A类不确定度探究［J］.大学物理，2012(1):35－38.

［8］宋宏权.牛顿环实验中不确定度的细致分析［J］.中国教育技术装备，2008(19):88－90.

［9］陈殿伟，盖啸尘，王显德，等.牛顿环实验测量结果不确定度的评定［J］.大学物理实验，2007(9):72－74.

［10］陈金太.大学物理实验［M］.厦门:厦门大学出版社，2005:3－13.

［11］李平舟，陈秀华，吴兴林.大学物理实验［M］.西安:西安电子科技大学出版社，2005:4－5.

［12］崔益和，殷长荣.物理实验［M］.苏州:苏州大学出版社，2008:4－5.