基于LabVIEW的心电信号插值算法分析

王宝珠，胡世帅，李晓娇

（河北工业大学 信息与工程学院，天津 300401）

基于LabVIEW的心电信号插值算法分析

王宝珠，胡世帅，李晓娇

（河北工业大学 信息与工程学院，天津 300401）

为了在LabVIEW平台下更方便的处理非均匀采样的心电信号，文中研究了心电信号的时域和频域插值算法。首先采用了拉格朗日插值法、牛顿插值法、埃尔米特插值法和三次样条插值法等四种时域插值方法，从算法精度、内存消耗和时间消耗三个方面做比较，得出埃尔米特插值法最为合适。最后又提出一种频域插值法：补零傅里叶频域插值法，来弥补原始心电信号频域分辨率不足的缺点。

LabVIEW；心电信号；插值算法

通常经过硬件采集的心电信号都不是均匀采样的信号，数字信号处理技术里面处理均匀采样的信号比处理非均匀采样的信号要简便的很多[1]，而且对于虚拟仪器开发平台——LabVIEW，其所提供的很多数字信号处理函数大都是针对均匀采样的数字信号设计的，所以很有必要将原始的非均匀采样信号通过时域插值变为均匀采样信号。另外由于在时域采样过程中，有可能会出现采样点偏移信号频率的情况，在对心电信号做频域分析时还有可能会出现频率分辨率不高的情况，因此对原始信号做频域插值也是有必要的。

1 原始心电信号数据分析和功率谱分析

1.1 MIT-BIH心电数据库分析

近年来国内外对于心电信号的分析研究，多采用美国麻省理工学院提供的标准心电数据库：MIT-BIH数据库[2]。此数据库中的心电信号都是为非均匀采样得到。

以第100例数据为例，MIT-BIH数据库中的心电信号如表1所示。其中第一列数据为采样时间点，第二、三列数据为不同导联方式下的采样值。

1.2 原始心电信号功率谱分析

首先对原始的心电信号的功率谱做分析，计算出原始信号的总功率，保证插值后的信号功率与原始信号功率基本一致。

表1 原始心电信号数据Tab.1 Data of the original ECG signal

对于非均匀采样的心电信号，文中采用Lomb归一化周期图法[3-4]。Lomb归一化周期图定义为：

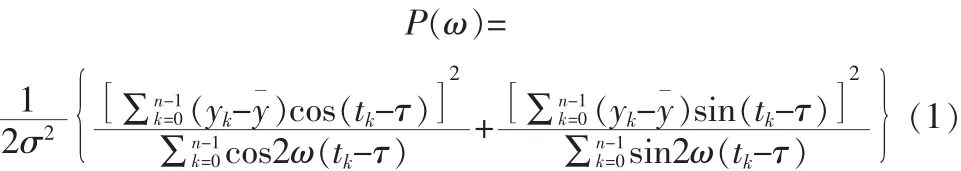
其中：

LabVIEW程序运行结果如图1所示。

图1 原始心电信号波形和功率谱Fig.1 Waveform and PSD of the original ECG signal

并且编程计算得到此原始心电信号的总功率（即将各个频率分量的功率相加）为：0.029 076 1。

2 几种时域插值算法的比较研究

根据表1心电信号数据特点，计划通过插值，将其变为时间间隔为0.001 s、采样率为1 kHz的均匀采样信号。

首先对所要解决的这个问题建立一个简单数学模型。下面将要介绍的几种插值法都是建立在这个数学模型上来求解的。

X={x0，x1，…，xn－1}，为原始心电信号的采样时间点序列。

Y={y0，y1，…，yn－1}，为原始心电信号的采样值序列。

对于采样时间点区间[xk，xk+1]来说，N=（xk+1－xk）/0.001－1 为在这个区间内需要插值的点的个数，则需要插值的点分别为（xk+1×0.001），…，（xk+N×0.001）。

假设存在一个函数 y=f（x）在区间[x0，xn－1]上有定义，使得对应xk点的函数值为yk。但由于f（x）肯定非常复杂，因此需要求解出一个简单函数 P（x）=yi，称 P（x）为 f（x）的插值函数，将求解插值函数P（x）的方法称为插值法。求解P（x）出后，相应再求出需要插值的点的值，最后得到时间间隔为0.001 s、采样率为1 kHz的均匀采样信号。

2.1 拉格朗日插值

拉格朗日插值法的基本思想是把插值多项式P（x）的构造，转换为n个插值基函数li（x）的构造。其中一次拉格朗日插值又称为线性插值。

假定区间[Xk，Xk+1]及端点函数值yk和yk+1，求解线性插值多项式 L1（x），则：

其中:

经计算插值后信号的总功率为：0.028 665 3。与原始信号相比，总功率变换率为：－1.412%。

2.2 牛顿插值

牛顿插值是拉格朗日插值的改进。首先定义f（x）的k阶差商为:

根据差商的定义，牛顿插值公式为：

考虑到计算量和插值精度的要求，利用4阶牛顿插值公式来对心电信号进行插值。

运行程序，经计算牛顿插值后信号的总功率为：0.029 245 5。与原始信号相比，总功率变换率为：0.582%。

2.3 埃尔米特插值

埃尔米特（Hermit）插值法与上述插值法最大的不同是，它不但保证了在节点上的函数值是相等的，而且保证了节点处的导数值也是相等的[5]。

假设已知区间[Xk，Xk+1]及端点函数值 yk，yk+1，及端点处一阶导数值 tk，tk+1，求解插值多项式 H（x），其中 H（x）必然满足条件：

则埃尔米特插值多项式为：

其中：

经计算，埃尔米特插值后信号的总功率为：0.028 990 1。与原始信号相比，总功率变换率为：－0.296%。

2.4 三次样条插值

将富有弹性的细长铁丝一段固定在墙上，由于重力的作用，然后另一端会自由向下弯曲，这时弯曲的铁丝这样的曲线就称为样条曲线。使用三次样条（Spline）插值来对心电信号进行插值，可以最大程度地保证心电波形足够的平滑。

假设已知函数 f（x），并且其在节点 a=x0＜x1＜…＜xn－1=b 处的函数值满足条件f（x）=yk。则插值多项式为：

其中：

计算三次样条插值后信号的总功率为：0.029 064 4。与原始信号相比，总功率变换率为：-0.040%。

2.5 时域插值算法结果分析

上述几种算法各有其特点，优缺点在每个算法的介绍中也提及，就不再赘述。运行利用各个插值功率变化率，比较数据如表2所示。

表2 算法性能比较Tab.2 Comparison of the algorithm performance

从此表格可以得出以下几点：

1）利用Lomb算法估计原始信号功率谱时，消耗的时间和内存远远大于利用FFT估计均匀采样的数据信号的功率谱，再次论证了插值的必要性。

2）拉格朗日插值、牛顿插值、埃尔米特插值和三次样条插值，四种算法的运行时间和消耗内存越来越大，这也是与其算法的复杂程度相匹配的。

3）从插值前后总功率的变化量来看，4种插值算法的精度越来越高，但即便精度最低的拉格朗日算法其功率变化量也只有1.4%，所损失的这点功率也是可以接受的。

综上所述，可以看到3次样条插值虽然其算法的精度非常高，但是却在运行时间和内存消耗上付出了代价，因此并不合适；剩余3种算法，当在实时性要求比较高的场合时，建议采用拉格朗日算法或者牛顿算法；当对精度要求比较高的时候，建议采用埃尔米特插值算法。

3 频域插值

对心电信号做分析处理过程中，无论是功率谱估计还是去噪滤波等大都是在频域处理的，而心电信号的采样都是做的时域采样，因此很有可能采样位置是偏移信号频率的[6]。

另外当对数字信号在频域做非常细致的分析时，很有可能会遇到频率分辨率不够高的情况[7]。为了解决以上可能会遇到的情况，需要对数字信号做频域插值处理。

补零傅里叶频域插值法是一种简单有效的插值算法。先对原始数字信号做离散傅里叶变换，根据心电信号的特点（信号主要能量都集中在低频部分，高频分量很小）选择在其高频部分补零。补零处理完毕后再变换到时域即可。

由于在LabVIEW中做频域插值处理的信号也须为均匀采样信号。文中是利用埃尔米特插值后的数字信号对其做频域插值，使其频域分辨率扩大为原来的2倍，实际应用中可根据需要扩大为不同的倍数。先后经埃尔米特和频域插值后的心电信号的时域波形和功率谱如图2所示。

插值后信号的总功率为：0.028 990 1。这个数值是与埃尔米特插值后信号的总功率值一样的，因为此插值法只是做的补零处理。

图2 时域和频域插值后结果Fig.2 Results of the time-domain and frequency-domain interpolation

4 结 论

时域插值能够将非均匀的原始信号变为均匀采样信号，其中牛顿插值法和埃尔米特插值法能够分别满足算法速度和精度的不同要求。补零傅里叶插值法是一种简单有效的频域插值法，能够根据需求提高心电信号频率分辨率。

文中针对心电信号所做的插值算法分析，其研究思路和方法对于其他生理信号，比如脑电信号、肌电信号，也是同样适用的。

[1]于璐，索永宽，沙宪政.基于虚拟仪器的生理信号采集分析系统[J].生物医学工程与临床，2011，5（3）:219-222.

YU Lu，SUO Yong-kuan，SHA Xian-zheng.Physiological signal acquisition and analysis system based on virtual instrument[J].Biomedical Engineering and Clinical Medicine，2011，5（3）:219-222.

[2]宋喜国，邓亲恺.MIT-BIH心率失常数据库的识读及应用[J].中国医学物理学杂志，2004，21（4）:230-232.

SONG Xi-guo，DENG Qin-kai.ON the format of MIT-BIH arrhythmia database[J].Chinese Journal of Medical Physics，2004，21（4）:230-232.

[3]韩君.基于LabVIEW的心电信号检测实验系统设计[J].中国医疗设备，2008（10）：55-56.

HAN Jun.Design of ECG-detecting experimental system based on LabVIEW[J].China Medical Devices，2008（10）:55-56.

[4]Sahambi J S，Tandon S N，Bhatt R K.Using wavelet transforms for ECG characterization[J].IEEE Engineering in Medicine and Biology Magzine，1997，16（1）:77-83.

[5]刘建中.高阶Hermite插值的一致收敛性及逼近阶[J].广西师范大学学报，1992（1）:30-33.

LIU Jian-zhong.On the uniform convergence and approximation order of higher order hermite interpolation[J].Journal of Guangxi Normal University，1992（1）:30-33.

[6]于璐，张勇德，沙宪政.LabVIEW和Matlab混合编程方法在生物医学信号分析中的应用[J].中国医疗器械杂志研究与论著，2011，35（1）:15-18.

YU Lu，ZHANG Yong-de，SHA Xian-zheng.Application of the mixed programming with labview and matlab in biomedical signal analysis[J].Chinese Journal of Medical Instrumentation，2011，35（1）:15-18.

[7]王坤.基于SVPWM的STATCOM设计及实现[J].陕西电力，2011（1）：11-15.

WANG Kun.SVPWM based design and realization of STATCOM[J].Shaanxi Electric Power，2011（1）：11-15.

Research on ECG interpolation algorithm based on LabVIEW

WANG Bao-zhu， HU Shi-shuai， LI Xiao-jiao
（College of Information Science and Engineering， Hebei University of Technology， Tianjin 300401， China）

In order to processing the non-uniform sampling electrocardiogram （ECG） signal based on LabVIEW ，this paper analyzed the time-domain and frequency-domain interpolation algorithm for ECG signal.Firstly，we compared four time-domain interpolation algorithm:Lagrange interpolation， Newton interpolation， Hermite interpolation and cubic spline interpolation from three angles of calculation accuracy， memory consumption and program execution time， then the result is that Hermite interpolation algorithm is the most suitable.Also we proposed a frequency-domain interpolation algorithm named Fourier transform with zero-padding interpolation algorithm，which is can improve the frequency resolution.

LabVIEW；ECG signal；interpolation algorithm

TP911.6

A

1674－6236（2013）04-0085-03

2012-10-12稿件编号201210084

王宝珠（1963—），女，天津人，教授，硕士生导师。研究方向：信息检测与处理、图像处理、多媒体通信。