最优噪声整形滤波器的设计
2013-07-13周静雷朱增友
周静雷,朱增友
(西安工程大学 电子信息学院,陕西 西安 710048)
最优噪声整形滤波器的设计
周静雷,朱增友
(西安工程大学 电子信息学院,陕西 西安 710048)
在需要对信号进行再量化的场合,可以通过加入dither来避免小信号再量化所产生的谐波失真,但同时会使噪声功率增加。这种情况下,可以利用人耳的心理声学特性,通过噪声整形来降低噪声的可闻性,提高实际的信噪比,改善音质。本文提出了两种新的设计最优噪声整形滤波器的方法-遗传算法和非线性优化算法,并分别实现了原采样率下和过采样率下基于心理声学模型的最优噪声整形滤波的设计。结果证明,该方法灵活方便、实现效果良好。
dither;心理声学;噪声整形;遗传算法;非线性优化算法;上采样
在数字音频应用中,经常会遇到信号的再量化。比如,对于20或24 bit的音频文件必须先将其降16 bit才能在CD机上播放[1-2]。再如,在数字音频信号处理中,任何一种处理都可以归结为某种形式的滤波,而滤波过程中需要做大量的乘累积运算。对于一般的应用,比如采用定点DSP处理时,首先需要将滤波器系数截断成定点,而且在运算过程中又不可避免进行多次四舍五入处理,这样一来误差不断积累,会导致输出端音质的严重恶化。因此,对于高端音频应用,一般都是采用高性能的浮点处理器进行内部处理,处理完毕后再将结果按照需要降到相应的格式,如16 bit[3]。该过程也相当于信号的再量化。
再量化不可避免地引入误差。当信号幅度较小时,由于再量化,在输出端可能会产生严重的谐波失真,使声音听起来出现“怪音”;当信号幅度逐渐衰减到0时,由于再量化声音会断断续续,极不自然。如果在再量化之前加入适当的dither(如 TPDF 型 dither)[2],则可以消除谐波失真,并保留微弱信息,使声音听起来更加自然,但它同时会增加噪声功率。这种请况下,可以利用人耳的心理声学特性,通过噪声整形将噪声功率转移到人耳不敏感的频带内,使接收到的总的加权噪声功率最小,从而提高输出端实际的信噪比。
噪声整形技术的关键是设计出满足心理声学特性的噪声整形滤波器。文献[1][4]分别讨论了利用希尔伯特变换和最小二乘理论实现非过采样下噪声整形滤波器的设计方法。本文首先利用遗传算法完成了最优噪声整形滤波器的设计,并将噪声整形技术应用到上采样处理中,实现了过采样下最优噪声整形滤波器的设计。此外,针对遗传算法优化速度慢的缺点,还探讨了采用非线性优化算法设计最优噪声整形滤波器的方法,分别实现了原采样率和过采样下最优噪声整形滤波器的设计。
1 噪声整形的原理
噪声整形的基本思想是根据人耳对噪声的敏感程度随着频率的变化而不同的心理声学特性,将大部分噪声功率转移到人耳相对不敏感的频带,从而使接受到的可闻噪声功率最小[1-5]。基于心理声学的噪声整形是根据听觉加权曲线,通过反馈在量化过程中产生的噪声,将噪声谱整形成类似加权曲线的倒转形式,从而使噪声在整个频带上都具有相同的可闻性。听觉加权曲线是用来近似不同频率处噪声的相对可闻性,常用的加权曲线有改进的E加权曲线和F加权曲线,文中将采用F加权曲线进行讨论。由于F加权曲线在直流附近和高频处的极大衰减,会导致此处未加权噪声功率无法接受,因此一般在所有频段加上一个小的正常数对其进行修正,这样就得到修正的F加权曲线[1]。
噪声整形的原理框图如图1所示。
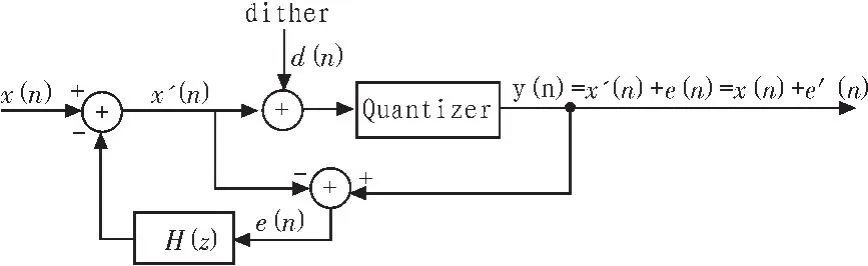
图1 噪声整形原理框图Fig.1 Schematic diagram of noise shaping
图中,H(z)是误差反馈滤波器也即噪声整形滤波器,其单位脉冲响应记为 h(n),e(n)代表量化误差信号,e′(n)是输出端的加性噪声,由图中所示信号节点可以得到:
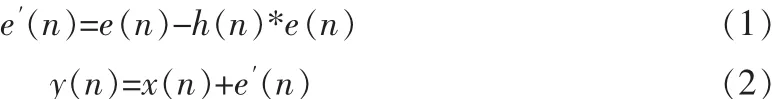
变换到Z域得:
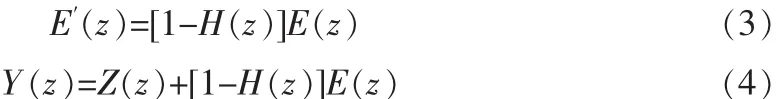
可以看到,量化误差信号被误差反馈滤波器H(z)决定的系统 1-H(z)所整形,而输入信号未受影响。 用 z=ejω代入(3)式可得输出端噪声信号的功率谱:
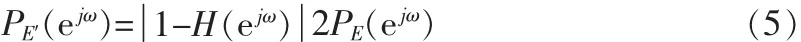
为了实现输出端噪声最小可闻,H(ejω)要设计成使得总的听觉加权噪声功率Nω最小:
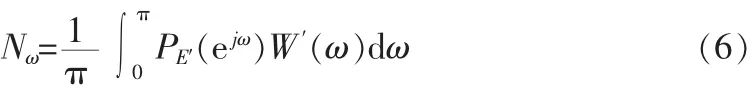
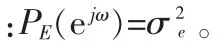

其中:
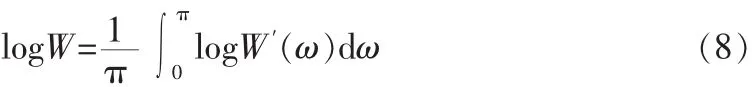
用W进行规范化处理以保证当1-H(z)的幅度以对数表示时曲线在0 dB以上的面积跟以下的面积相等。
2 基于遗传算法的最优噪声整形滤波器的设计
由图2可知,误差信号只有在再量化后才可用,因此必须有一个采样点的延时,故的一般表达式为:

当对于所有的i都有bi=0就对应着一种特殊的滤波器-FIR滤波器,由此可得到1-H(z)的一般形式如下:
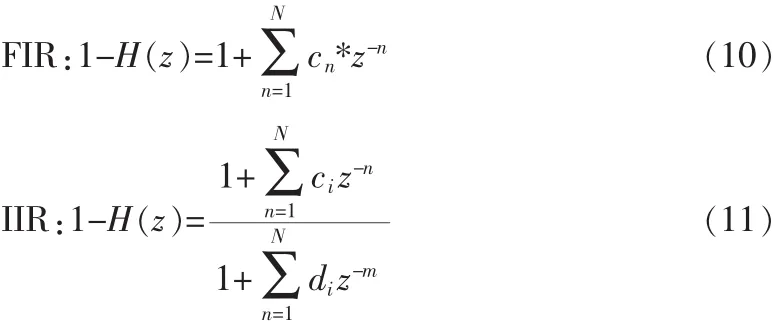
其中,1-H(z)必须是最小相位滤波器[1-2,4]。 采用遗传算法来求解最优噪声整形滤波器的步骤为:1)将由式(7)、(8)决定的曲线进行开方,并将其作为目标曲线 T(f);2)由(10)、(11)式,根据需要选择适当的滤波器阶数以及滤波器结构(级联型或直接型),并将 z=ejw(w=2×pi×f/fs)带入式中,求得 1-H(z)的含待定系数的幅度谱H(f);3)在频率轴上等间隔地取一定数量的点将它们离散化,将二者相对误差的平方和(或取对数后的方差)作为适合度函数。由于1-H(z)必须是最小相位的,因此将零、极点距原点的距离小于1作为约束条件。设定合适的参数进行优化设计,通过若干次优化即可得到最优噪声整形滤波器的系数。
图2是在采样率为44.1 kHz下,通过选择k=10-4,α=0.5得到修正加权曲线 W′(ω),由式(7)、(8)得到的目标曲线。 图3中虚线为利用遗传算法优化得到的9阶FIR噪声整形滤波器H(z)所对应的1-H(z)的功率谱特性曲线。可以看出,实际设计曲线与目标曲线在低频段吻合的比较好,在直流及高频段有些许差别。
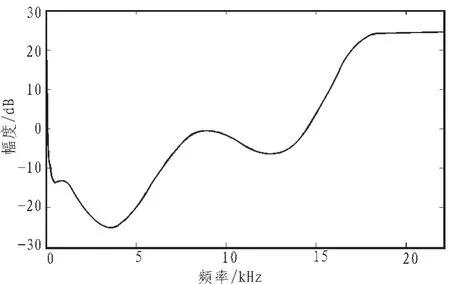
图2 原采样率下目标曲线Fig.2 Target curve of non-oversampling
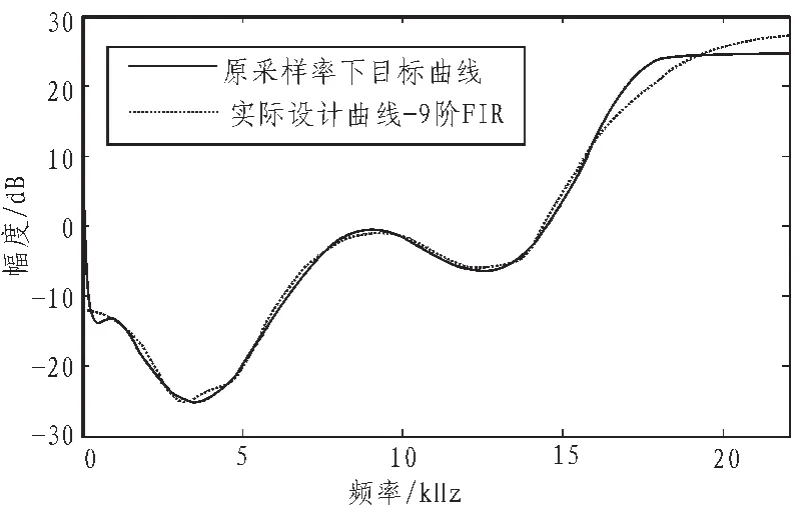
图3 原采样率下实际设计曲线与目标曲线比较 (遗传算法-9阶FIR)Fig.3 Comparison of actual design curve and the target curve in nonoversampling (Genetic algorithm-9th FIR)
3 过采样下最优噪声整形滤波器的设计
在数字音频信号处理中,上采样(Upsampling)是一种重要的提升音质的手段。它是通过某种算法在以fs为采样率的原始输入相邻样点之间插入L-1个新的样点,使输出采样率变成L.fs。通过上采样可以将原量化噪声功率分散到更宽的频带,从而减小听觉频带内的噪声功率,同时可以降低DAC后级联的模拟低通滤波器的技术指标要求,降低其实现难度和成本。因此,目前的解码系统在DAC之前一般都要先进行上采样,但基本都是采用集成芯片实现,由于面积限制,其技术指标往往不能满足高端音频应用的需求。这种情况下可以考虑采用DSP或FPGA等来专门实现上采样。由于上采样中同样需要做大量的运算,也需要对运算结果进行再量化处理。这时,可以加入处理并采用噪声整形技术来进一步降低噪声。这就需要考虑过采样下的最优噪声整形滤波器的设计。为简便期间,文中仅讨论2倍过采样的情形。
由于以上采用的F加权曲线仅仅涉及到0~fs/2频率范围,因此必须将该曲线加以扩展,使之在0~fs内都有定义。一种简单的方法是认为噪声fs/2~fs在频带内具有相同的可闻性,根据“1-H(z)的幅度以对数表示时0 dB以上跟0 dB以下面积相等”的原则,便可得到2倍过采样下的目标曲线(如图4所示)。图5中虚线是采用上述遗传算法优化得到的实际设计曲线,它是24阶的FIR滤波器。可以看到在听觉范围内二者吻合的很好,在高于fs/2的频段实际设计曲线有逐渐衰减的纹波出现。
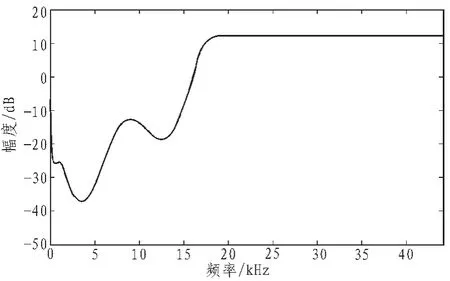
图4 2倍过采样下目标曲线Fig.4 Actual design curve in 2 times oversampling
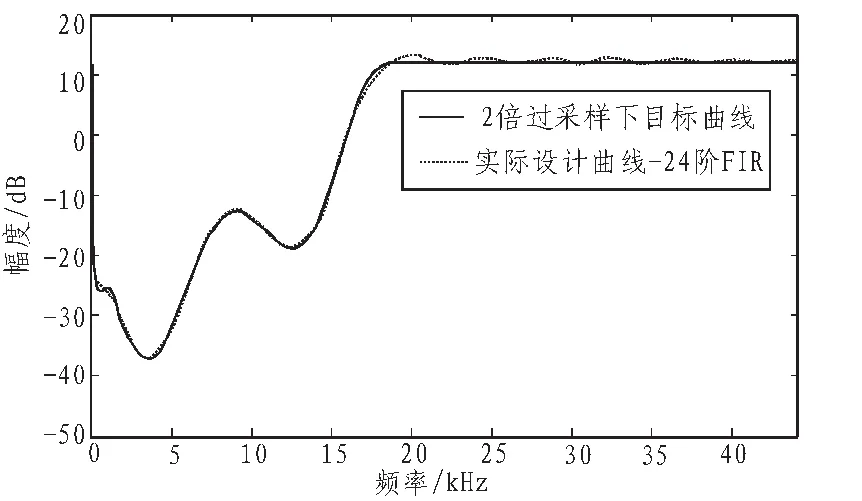
图5 2倍过采样下实际设计曲线与目标曲线对比(遗传算法-24阶FIR)Fig.5 Comparison of actual design curve and the target curve in 2 times oversampling (nonlinear optimization -10th IIR)
4 基于非线性优化算法的最优噪声整形滤波器的设计
前面采用遗传算法,利用FIR滤波器设计最优噪声整形滤波器。可以看到,实际设计曲线与目标曲线在大部分频带内吻合的比较好,而在高频段与目标曲线有些差距,尤其是在2倍过采样下在高于fs/2频带内出现了纹波。理论上,可以采用更高阶的滤波器来使得实际设计曲线与目标曲线更加吻合。然而,当待求滤波器系数比较多时利用遗传算法优化起来会非常耗时且不容易得到满意结果,并且滤波器阶数太高会造成实时实现的困难。针对遗传算法优化速度慢的缺点,下面采用另一种优化算法—非线性优化算法进行优化设计。非线性优化算法是以使输出序列的均方差最小为优化准则进行非线性优化的,优化速度比较快;此外,由于噪声整形滤波器只会改变噪声谱,不会对有用信号造成影响,因此可以使用IIR型滤波器来代替FIR型滤波器以降低滤波器阶数。
采用非线性优化算法实现时,1-H(z)采用级联结构,且由于它的特殊性(见式(13)),每级的一般形式为[1 c1 c2 1 d1 d2],c1、c2、d1、d2 分别为分子分母待定系数。 由于滤波器的系数均为实数,故其零极点或以共轭对形式存在或位于实轴上,因此将每一级的形式设为以下两种形式之一:[1-2×x(1)×cos(x(2))x(1)^21-2×x(3)×cos(x(4))x(3)^2]或 [1-x(5)0 1-x(6)0];其中,x(1)、x(3)、x(5)、x(6)表示零极点与原点之间的距离(半径),x(2)、x(4)表示零极点与原点的连线与正实轴的夹角(相角),它们都是需要求出的参数。直接将半径和相角作为待求参数,这样有利于零极点位置的调整,能够快速地得出正确结果。目标曲线的离散序列为,含待定系数的设计曲线的离散序列为,则返回值序列。
此外,还需要设定合适的边界和起始点。这里,由于直接将半径和相角作为待定参数,为了满足最小相位条件,将半径参数的边界设为[0 1],相角参数的边界设为[0 π],起始点均设为0,采用这种设置方式能够快速得到最优结果。图6、图7分别是原采样率下实际设计曲线以及它与目标曲线的对比,图8、图9分别是2倍过采样下实际设计曲线以及它与目标曲线的比较。采用的均为10阶的IIR滤波器,而1-H(z)的零极点都位于单位圆内部,因此它们是稳定的且是最小相位的。
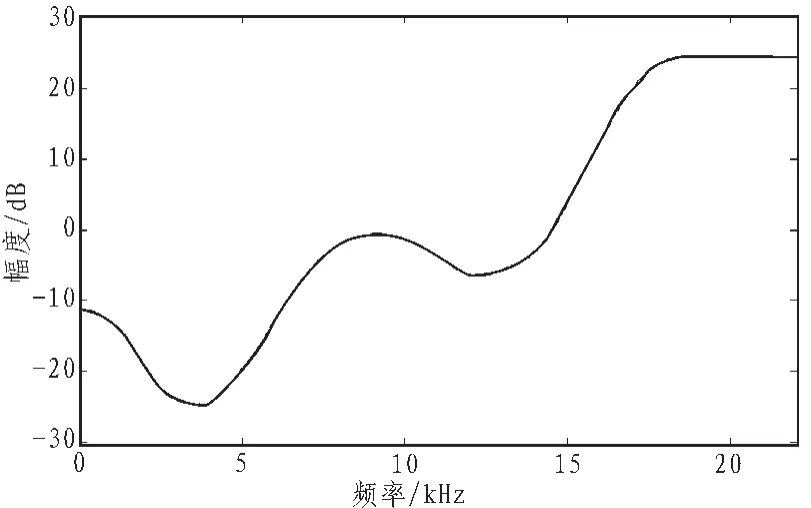
图6 原采样率下实际设计曲线(非线性优化-10阶IIR)Fig.6 Actual design curve in non-oversampling(nonlinear optimization-10th IIR)
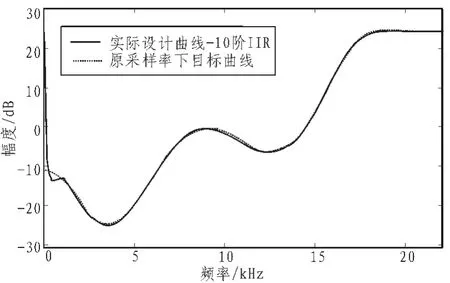
图7 原采样率下实际设计曲线与目标曲线对比(非线性优化-10阶IIR)Fig.7 Comparison of actual design curve and the target curve in nonoversampling (nonlinear optimization -10th IIR)
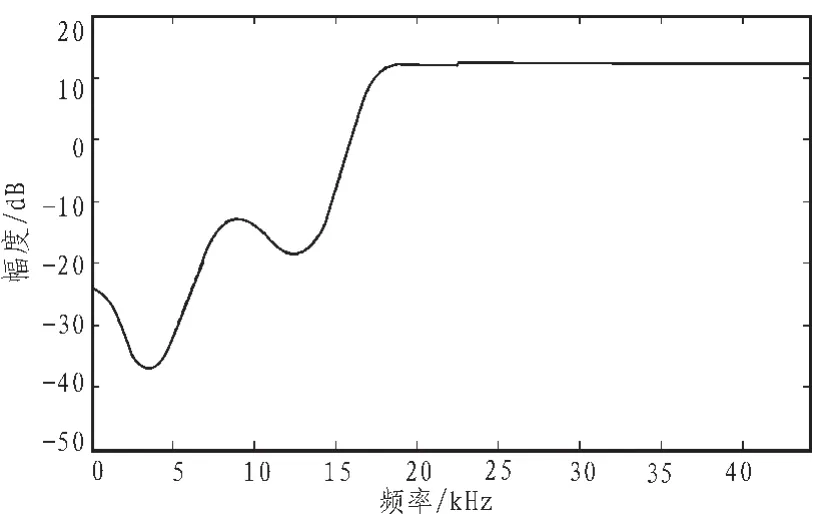
图8 2倍过采样下实际设计曲线(非线性优化-10阶IIR)Fig.8 Actual design curve in 2 times oversampling(nonlinear optimization-10th IIR)
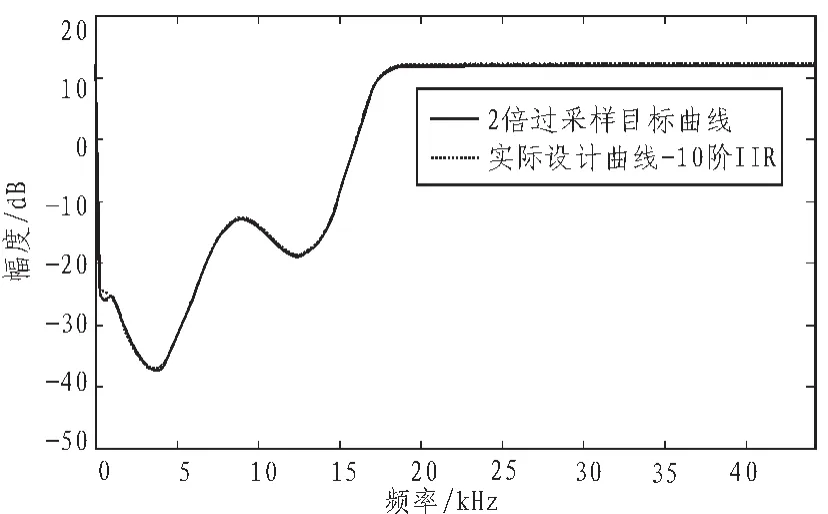
图9 2倍过采样下实际设计曲线与目标曲线对比(非线性优化-10阶IIR)Fig.9 Comparison of actual design curve and the target curve in 2 times oversampling (nonlinear optimization -10th IIR)
可以看到,无论是在非过采样还是过采样下,采用非线性优化算法得到的实际设计曲线与目标曲线都非常吻合,且滤波器的阶数都在可接受范围内。2倍过采样下的实际设计曲线,在高频段没有出现纹波,只有在直流附近与目标曲线不符,然而这正是我们想要的结果。因为,实际设计时我们舍弃了0~200 Hz频段内对应的点,而采其余的点作为参考点进行设计以避免在直流附近出现大的未加权噪声功率。实际设计曲线越接近目标曲线,经过整形后的噪声谱的形状将越符合近人耳的心理声学特性,效果也越好。
5 结束语
再量化是数字音频应用中经常面对的问题,通过在再量化之前适当的加入dither并采用噪声整形技术不仅可以消除失真,保留微弱信息,改善听感,并且可以最大限度地降低噪声的可闻性。噪声整形技术的关键在于基于心理声学的噪声整形滤波器的设计,本文提出的两种设计方法,不仅简便灵活,而且实现效果良好,可以应用在实际的数字音频信号处理中。
[1]Wannamaker R A.Psycho-acoustically optimal noise shaping[C]//Proceedings of 89th AES Convention.Log Angeles:[s.n.],1990:21-25.
[2]Hicks C.The application of Dither and Noise-Shaping to Nyquist-Rate Digital Audio:an Introduction[EB/OL].[2011-8-20].http://www.benchmarkmedia.com/sites/default/files/documents/ditherap.pdf.
[3]冼剑锋.噪声并不讨厌—浅谈“高频振动”(DITHER)技术[J].音响技术,2002(3):51-52.
XIAN Jian-feng.Noise is not hate-Discussion on DITHER technology[J].Audio technology,2002(3):51-52.
[4]Verhelst W,Koning D D.Least squares theory and design of optimalnoise shaping filters [C]//Proceedingsof22nd International Conference AES on Virtual,Synthetic and Entertainment Audio.[s:l.]:[s:n.],2001.
[5]Lipshitz S P,Vanderkooy J,Wannamaker R A.Minimally-Audible NoiseShaping[C]//proceedings of J.Audio Eng.Soc 1991.Montreux:[s.n.],1991,Preprint 2916.
[6]Verhelst W,Koning D D.Noise shaping filter design for minimally audible signal requantization[J].IEEE Workshop on Application of Signal Processing to Audio and Acoustics,2001:21-24.
[7]Lipshitz S P,Vanderkooy J.Why 1Bit sigma-delta conversion is unsuitable for high-quality applications[C]//proceedings of the110thConventionofAudioEngineeringSociety.Amsterdam:[s.n.],2001,Paper 5395.
[8]Dejan G.Ciric,Milos Markovic, Branko Stojic.Improvement in design of noise shaping filters[J].Cent.Eur.J.Eng.2012,2(2):224-230.
[9]Hahn J.Design approaches for psychoacoustical in-band noise shaping filters[C]//proceedings of 126th Convention of J.Audio Eng.Soc.Munich:[s:n.],2009,Paper 7800.
Design of optimal noise shaping filters
ZHOU Jing-lei,ZHU Zeng-you
(Electronic Information College, Xi'an Polytechnic University, Xi’an 710048, China)
In the occasion that signal needed to be re-quantified,adding proper dither can avoid the harmonic distortion generated in small signal’s re-quantization, but it will make noise power increase at the same time.In this case, we can take advantage of human ear’s psychoacoustic characteristics, apply noise shaping technology to reduce the noise’s audibility,then improve actual signal to noise ratio (SNR)and improve sound quality.This paper presents two new methods to design optimal noise shaping filters-genetic algorithm and nonlinear optimization algorithm,and realized the design of optimal noise shaping filters based on psychoacoustic model respectively under original sampling rate and over-sampling rate.It proves that these methods are flexible and convenient,can achieve good results.
dither;psychoacoustics;noise shaping;genetic algorithm;nonlinear optimization algorithm;upsampling
TN912.2
A
1674-6236(2013)04-0075-04
2012-09-14稿件编号201209094
陕西省教育厅专项科研计划项目(11JK0548)
周静雷(1978—),男,陕西西安人,博士,副教授。研究方向:声频信号处理,电声学。
