逆向工程中对离散点云的特征识别算法探究

张 萍

（上海大学巴士汽车学院，上海 201314）

0 引言

逆向工程可以把成品转换为工程模型和概念模型。逆向设计过程中，借助激光扫描数据技术，可以获取包含物体信息的离散点云数据。根据离散点云数据中点的排列、密度、组织和分布特点，点云数据常被分为如下几部分离散的数据：扫描调运数据线、网格点云和多边形点云[1]。而数据处理的过程通常包括点云合并、降噪、数据消减和表面识别等。数据处理将直接影响后续数据的重构的质量和效率[2]。将小波变换应用于离散点云的数据处理正处于研究中。

小波分析是当前应用数学和工程学科中一个迅速发展的新领域，经过近10年的探索研究，重要的数学形式化体系已经建立，理论基础更加扎实。与Fourier变换相比，小波变换是空间(时间)和频率的局部变换，因而能有效地从信号中提取信息。通过伸缩和平移等运算功能可对函数或信号进行多尺度的细化分析，解决了Fourier变换不能解决的许多困难问题[3]。小波变换是时间—尺度分析和多分辨分析的一种新技术，它在信号分析、语音合成、图像识别、计算机视觉、数据压缩、地震勘探、大气与海洋波分析等方面的研究都取得了有科学意义和应用价值的成果[4-5]。

1 点云数据的小波表示方法

通常可以使用yi=f(xi)来表示二维的离散点云数据，很显然离散点云数据信号的能量是有限的。因此我们可以把小波变换理论应用到离散点云数据的处理当中。

L2（R）空间，即平方可积的函数空间，它可以被分解为无限个正交直和的形式，如下公式

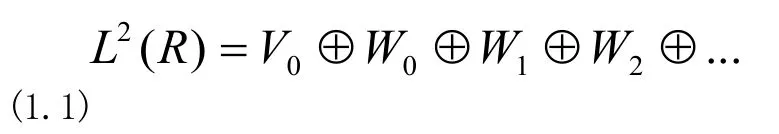
因此可以唯一展开离散点云数据yi=f(xi)，yi∈L2（R）为：

小波变换通常使用函数空间L2（R）中的基来表现其中的任意一个信号的，对于离散点云数据的处理需要确定母小波函数。通过伸缩和平移母小波函数，可以使用如下所示的公式来定义离散点云的小波分析函数

式1.3中,参数s为尺度参数，参数τ表示平移参数，*表示取共轭函数。可以通过小波变换将一维函数的离散点云数据(xi,yi)映射成二维函数Wf（s,τ）。同样，逆连续小波变换离散点云数据则能通过ψ(s,τ)可以得出。

2 离散点云数据的小波分解

将给定的数据点坐标值展开成小波的平移和伸缩之和，该方法本质上是将离散点云数据空间转换成小波基的表示形式。点云数据的小波构造块不仅需要满足小波的正交性，还应该满足小波平移和伸缩系的正交性，这样就可以按照尺度将离散点云数据展开成不同的特征成分。

使用尺度函数的线性组合，即近似函数，来近似的表示离散的点云数据，使用级来定义近似的精度，并且第0级的精度最高。

由于尺度函数以及小波的组合组成了更高一层空间的基，即V0+W0构成了W1的基，以此类推得出下式：

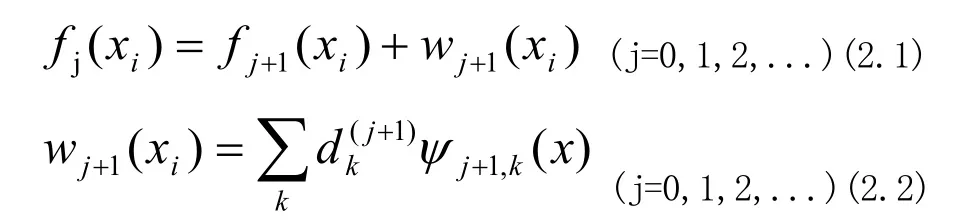
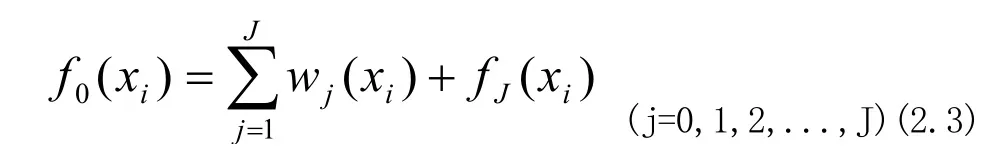
从式2.3中，我们可以看出，可以通过相加第J级的近似函数fJ(xi)和粗略近似所累计的丢失成分，恢复离散点云数据f0(xi)的原始点云数据f0(xi)。此外，可以使用的线性组合表示离散点云数据的尺度函数ϕ(x)，式2.4被称为尺度函数的二尺度关系。

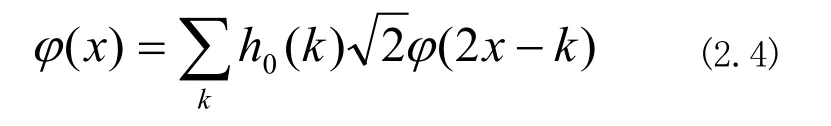
类似有小波函数的二尺度关系如下式：

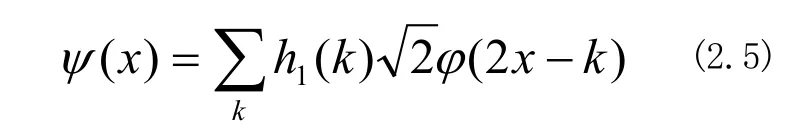
cj（k）可以由第j级的小波函数的点积和点云数据信号得到

综合式2.4、2.5和2.6可以得到如下两式：

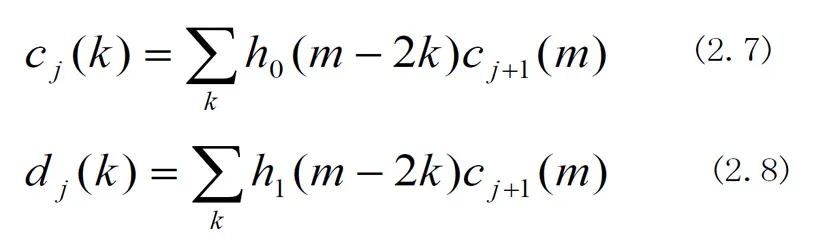
按照如上两式所示，如果滤波器的系数h0和h1已经确定了，则可以发现第j-1级的尺度系数和小波系数可由第j级的尺度系数计算出，依次类推，所有较低分辨率下的系数就可以计算出来，一共可以获得1个尺度系数和2n+1个小波系数；类似的重构过程为上述过程的逆过程。综上所述，可以用第1级到第J级的一共J个分辨率的小波表示离散点云数据f0(xi)。

经过上述的过程分解离散点云数据，加上利用小波变换的两个方向上的联合分析的特征，能自动的把点云数据按照尺度关系分解成不同的特征部分[6-7]，从而能够在后续进行进一步的应用。

3 二维离散点云的特征识别算法

二维的离散点数据是以某一个坐标轴为自变量的离散函数yi=f(xi),可以将一维的小波变换应用到此数据集上。连续信号在重构的时候需要基于尺度参数和基于平移参数的无限积分，而离散的小波变换的这两个参数需要二值化。

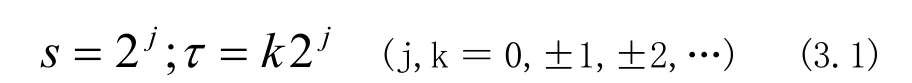
对参数s和τ进行二进制分割，即可对连续小波进行离散化后的二阶小波

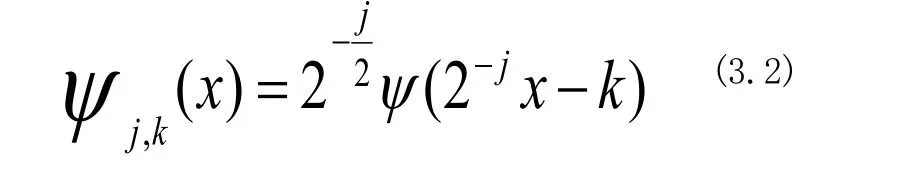
对二维的离散点进行小波变换时，一般要求等间距的偶数个采样点，为了方便后面进行的的分解和重构。基于小波变换的基本理论，本文提出了如下步骤对二维的离散点进行小波变换：

（1）选择对应的小波基以及相应的滤波器；（2）确定需要达到的尺度阈值；（3）依据离散点的个数来确定初始分解的级数，同时，把这个采样值作为尺度系数的初始值；（4）依据一定的顺序对数据进行排序；（5）求解y坐标的数据值和小波的相关值；（6）重复执行第5步，直到整个数据域被覆盖时才停止；（7）对下一级的尺度，重复步骤5和步骤6；（8）继续分解，直到达到预先设定的尺度阈值，然后再执行步骤5和步骤6，至此小波的分解过程才完成；（9）可以利用第j-1级的尺度系数和小波系数构造出第j级的尺度系数；（10）重复执行步骤9，直到完成所有数据的重构；

4 三维离散点云的特征识别算法

三维离散点云数据和二维离散点数据极其相似，可以把三维离散点云数据看作是以两个坐标轴为自变量的二维离散函数zi=f(xi,yi)，然后就可以将二维的离散点云数据的小波变换应用到三维的离散点云数据集上。然而对二维的离散点进行小波变换时同样需要尺度参数和小波参数的二值化，也就事要求在x和y方向上分别满足按照2j和2k进行等间距采样，为了方便后续的分解和重构。

二维小波变换就是将二维信号展开成的四种小波和尺度的张量级数的形式，具体的分解过程如下∶

首先进行水平方向上的离散小波变换，其中pk和qk分别表示低通滤波器和高通滤波器，具体如下所示

然后对系数进行垂直方向上的离散小波变换，得到如下四个表达式：

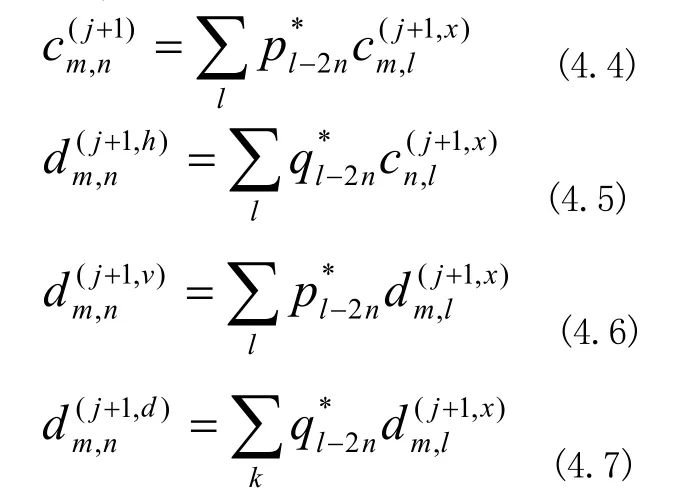
然后将4.2式和4.3式代入4.4，4.5，4.6，4.7这四个式子中，并展开成可以完成分解。三维离散点云数据的一次分解会产生4个子带,重复分解低频子带，可得到多尺度二维小波的子带。

基于上述理论，本文提出了按照以下步骤进行对三维离散点云数据的分解和重构：

(1) 选定相应的小波、滤波器和尺度阈值；(2) 对离散点云数据在两个坐标轴方向上分别进行等间距方式的采样，然后确定初始分解的级数； (3) 按照一定顺序对采样点进行排序；(4) 在水平方向上利用离散小波变换可以求出水平方向上的小波系数和尺度系数；（5）再对求解出的系数进行垂直方向上的离散小波变换，可以得到分解后的4个尺度和小波的联合系数；(6) 重复执行第5步，直到整个数据域完全被覆盖为止；(7) 对下一级的尺度，重复进行步骤4，5，6；(8) 继续分解直到达到所选定的尺度阈值为止，然后进行步骤4，5，6，7完成分解小波的过程；(9)由第j-1级的尺度系数和小波系数构造第j级的尺度系数；(10)重复第9步，直至完成所有数据的重构；

5 实例分析

根据提出的流程图和算法，本文通过对带有两个半圆弧的连续曲线上等间距采样128个采样点后得到原始测试数据，其中，点的采样间距为0.2，定义域为[0.352 26.652]。数据具体坐标如下表。

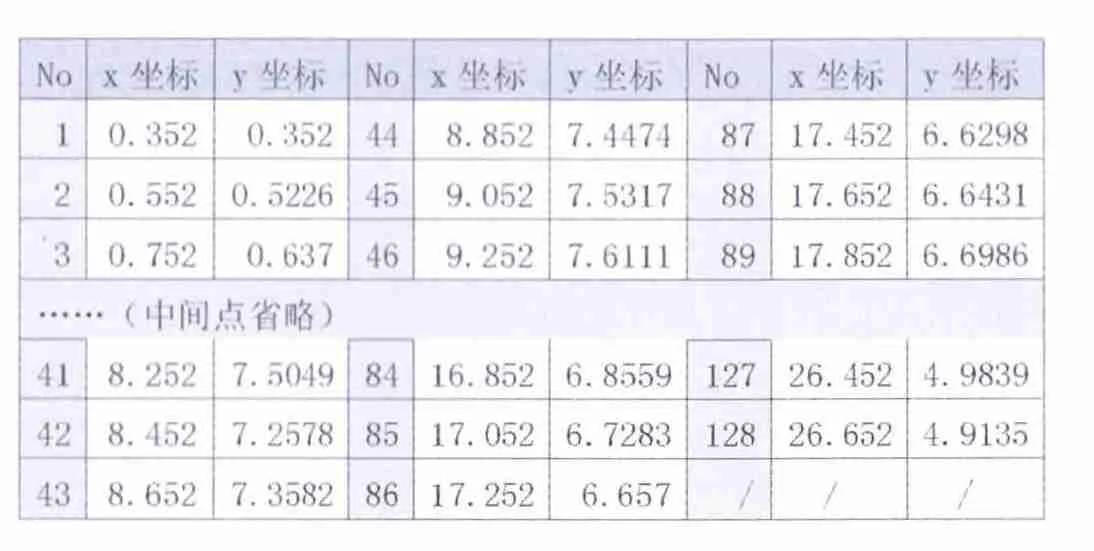
表5.1二维离散点数据

由于存在128个数据点数，这里记y坐标为c7k，确定初始尺度阈值为4，即把离散点数据依据3个尺度分成若干频率域，测试目标是将原始数据依据频率域分解成不同的成分，此处将两个半圆弧视为噪音数据。

计算步骤具体如下：尺度系数g7初始值为选取排序好的离散点云数据的yi；根据公式14的二尺度关系式，通过低通滤波器h0和c7的卷积计算c6

根据上式可计算出c6( 0)= 0.4540823，然后依次计算c6的其余分量，类似的可计算出d6的其余分量，根据以上方式迭代计算，可分别计算出c5和d5，以及c4和d4，直到符合尺度阈值要求。每次向下级尺度分解，新的小波系数和尺度系数分量的大小减少为一半，照此步骤计算，可以完成对离散点云数据的特征分解。

图5.1 离散点三个精度级的分解和重构

为实例在matlab7.0下进行测试，依据流程图所示，分别计算可得到离散点云分解后的3个精度级的小波系数和尺度系数 c6、d6、c5、d5、c4和d4，如图5.1、图5.2和图5.3所示，其中每一幅图中的第一子图表示初始的原始数据，第二子图表示重建后的数据，第三子图表示当前级别的低频分量，第四子图表示目前级别的高频分量∶

根据上述3图可以看到，对输入离散点云数据进行的第一次小波分解后，识别特征不甚明显，未达到目标值，则对此级别的尺度系数第二次分解，到第3次的分解，c4基本去除了噪声数据，完全达到了分解的目的，由于达到试验的目标，分解停止。此时，重建后的数据和初始的数据较好的重合，一些局部误差由舍入误差造成。

6 结语

本文参考小波变换的基本处理算法，将小波变换引入离散点云的处理中。通过应用小波变换，在处理过程中将点云数据划分成不同的频率特征信息，可以按照后期点云数据的不同应用，减少后期的离散点云数据的三维可视化过程中需要处理的数据量，具有一定的科学研究和工程应用价值。本文的研究虽然取得了初步的成功，但依然任重道远，尚有许多有待进一步深入进行的研究工作。

[1]张萍.基于逆向工程的轿车引擎盖设计[J].现代机械 ,2010,(01)

[2]邹鸿儒,刘占兵,周锋,鞠鲁粤.逆向工程中分层点云数据的拼合及精简[J].机电一体化 , 2006,(06).

[3]张宗平,刘贵忠,候兴松.一种改进的三维小波视频编码[J].西安交通大学学报∶自然科学版,2001,35(6)∶595.

[4]邵政,曾理, Hunziker Patrick R.高维图像的小波压缩方法[J].微机发展,2005,15(2)∶6.

[5]Daubechies I, Orthonormal I.Bases of compactly supported wavelets [J].Commun on Pure and Appl Math, 1988, 41(7)∶909.

[6]Mallat S.A theory for mult-i resolution approximation∶ the wavelet approximation[J].IEEE Trans,1989,11(7)∶674.

[7]Mallat S.Wavelet tour of signal processing [M].London∶ Academic Press,1998.