基于HHT的航空发动机气动失稳信号时频分析方法
2013-07-10郭贵喜王振华王洪祥高辉国薛秀生
郭贵喜,王振华,王洪祥,高辉国,薛秀生
(中航工业沈阳发动机设计研究所,沈阳110015)
基于HHT的航空发动机气动失稳信号时频分析方法
郭贵喜,王振华,王洪祥,高辉国,薛秀生
(中航工业沈阳发动机设计研究所,沈阳110015)
针对航空发动机工作范围内存在的气动失稳现象,运用希尔伯特-黄变换(HHT)分析其信号的时变特征;通过对其处理非线性、非平稳信号分析新方法与其他时频分析方法的对比,并对HHT存在的问题进行针对性解决,使其适应航空发动机气动失稳数据分析的要求。并在Labview平台上通过数字仿真试验实现和验证了HHT方法;结果表明:此算法准确有效;通过航空发动机工程试验数据的处理过程,验证了HHT在处理此类相关问题时的可行性、适用性,同时指出其仍然存在的缺陷。
时频分析;希尔伯特-黄变换;航空发动机;气动失稳
0 引言
航空发动机在其工作范围内存在“旋转失速”和“喘振”2类气动失稳现象,危害性极大。目前,发动机失稳现象是世界各国航空科研人员研究的重要课题。发动机气动失稳产生的流路内压力脉动本质上是一种非线性,非平稳信号,特别是在过渡过程中时变性很强。采用普通的处理线性、平稳信号的分析方法有非常大的局限性。目前大多数时频变换方法存在着不足,如所使用的基函数固定不变,难以准确匹配信号中的时频结构,而且时频分辨率还受到Heisenberg不确定性原理的限制[1-2]等。
本文应用希尔伯特-黄变换(HHT)对某型发动机压力脉动信号进行时频分析,提取信号的幅值和频率的时变特征,并将分析结果和傅里叶变换分析方法进行对比。
1 传统的时频分析方法
自然界中的信号几乎都是多种信号成分的叠加,既有平稳信号也有非平稳信号;信号既可能是线性的也可能是非线性的。传统的基于傅里叶变换的信号处理方法难以避免其局限性。它将信号从时域整个变换到频域,其谱分析仅能反映一段整体时间内所有频率与其幅值的对应关系,而对频率随时间的变化规律无法分析,也就是说它不能刻画出信号的频率等尺度在局部的瞬时特征。针对傅里叶变换不能反映信号瞬时特征的缺点,研究出多种时频分析方法。
1.1短时傅里叶变换
短时傅里叶变换(STFT)是1种最基本的时频分析方法。它通过1个滑动时窗,分段对信号进行傅里叶变换,实际上就是先对信号进行加窗处理,然后再进行傅里叶变换。这种方法在一定程度克服了傅里叶变换的缺点,实现了一定的分析信号局部特征的能力。但是窗口一旦选定,就不能任意更改,如果信号在时间或者频率上的变化小于窗口,窗口内信号平稳的假设就不能成立,信号的局部特征就不能被反映。而且它不能在时间和频率2个方面同时达到很高的分辨率,因此,短时傅里叶变换只适用于缓变信号的分析处理。
1.2小波变换
小波变换(WT)是20世纪80年代中后期发展起来的1种新型线性时频分析方法。该方法实现了窗口可调,在高频时使用窄窗口,在低频时使用宽窗口。正是基于这种多分辨率的思想,小波变换被誉为数学显微镜。但其本质上仍是是1种窗口可调的傅里叶变换,不可避免地仍具有窗函数的局限性。而且小波变换存在众多的的小波基函数,各种基函数使用的范围不同,造成小波基选择的困难,而且小波方法不具自适应性,一旦基函数选定后,就只能用来分析处理所有数据,这也是一直困扰小波变换研究应用的瓶颈。
1.3 Wigner-Ville分布
Wigner-Ville分布属于2次时频分析,是信号在时频平面上的联合功率谱,分辨率很高。该方法虽然克服了短时傅里叶变换的一些缺点,但在分析多分量复杂信号时,存在严重的交叉干扰,目前虽然有了一些消除干扰的方法,但都是以降低分辨率为代价。
1.4正弦曲线拟合
Choi[3]等首先使用正弦曲线拟合的方法来分析语音信号。该方法是利用1组不同频率的正弦曲线来拟合一时窗内信号,取拟合误差最小的正弦曲线为该信号的最佳拟合曲线。同时给出频率、振幅和相位信息,取拟合的剩余曲线重新拟合,直到拟合误差小到一定程度为止。这种方法可以用于多频率信号,但是该方法的拟合必须是在1个窗口内进行,因此时间分辨率不高,而且不同频率成分的信号会相互干扰,如果提取1个频率成分信号时通常就会破坏其他信号,只有选择的窗长是半个周期或整数倍附近时,才对其他信号影响较小。
2 希尔伯特-黄变换的理论和算法
2.1概述
1998年美国华裔科学家E.Huang提出了1种新型的非线性、非平稳信号的处理方法,即希尔伯特-黄变换(HHT)。该方法从信号自身特征出发,解决了Hilbert变换不能处理多值频率的限制,首先使用经验模态(EMD)方法把信号分解成一系列的本征模态函数(IMF),然后对这些IMF分量进行Hilbert变换,从而在时频平面上得到能量分布的Hilbert时频谱图。
该方法主要由“经验模态分解(EMD)”和“Hilbert谱”2部分组成。EMD方法自适应地将被分析信号分解成反映信号波动模式的若干个本征模态函数(IMF)。IMF没有固定的表达式,而是根据信号自身的波动情况自适应决定。对EMD的分解结果再进行Hilbert变换,计算瞬时频率和幅值,由此得到表征信号时间-频率-幅值的Hilbert谱。HHT算法执行效率高,具有良好的局部时频聚集性和自适应性。目前,该方法已经广泛应用于机械工程、通信电子、地球物理、生物医药等许多涉及信号分析的领域。
2.2 EMD分解方法
HHT主要包含EMD分解和Hilbert变换2个过程。根据信号的时间尺度,EMD方法自适应地通过1个“筛选过程”从被分析信号中提取生成其本身固有的1族本征模态函数(IMF),每个IMF必须满足以下2个条件:
(1)对于1列数据,极值点个数和过零点个数相等或至多相差1个;
(2)在任意点处,所有局部极大值点确定的上包络和由所有局部极小值点确定的下包络的均值为0。
根据这些条件,EMD的筛选过程主要包括以下3个步骤:
(1)首先找出原始信号X(t)的局部极大值和极小值,将其用3次样条函数求取信号的上下包络线:U(t)和V(t);
(2)计算上下包络线的平均曲线M(t)=[U(t)+V(t)]/2;
(3)用信号X(t)减去M(t)后得到1个去掉低频的剩余部分h1(t)=X(t)-M(t)。
一般来讲,h1(t)仍然不是1个平稳数据序列,即分解得到的h1(t)并不一定完全满足IMF条件[4],用h1(t)代替X(t),再求出上下包络线U1(t)和V1(t),重复上述过程,即
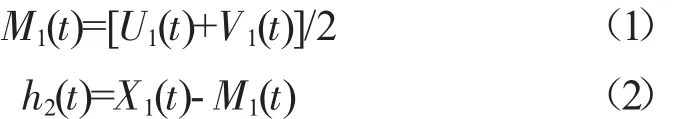
……

直到所有的hk(t)满足IMF条件。此时分解得到的第1个IMF,C1(t)和r1(t);即

必须指出,过多的重复该处理过程会导致模态分量变成纯粹的频率调制信号,因此,必须确定1个筛选停止准则。比如限制连续2次处理结果之间的标准差σ的大小来实现。
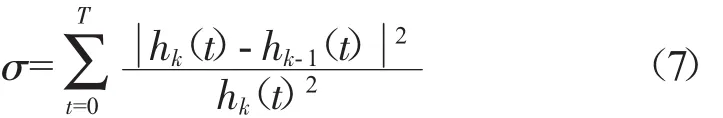
一般选取σ=0.2~0.4。
对信号的剩余部分r1(t)继续进行EMD分解,直到剩余部分为1个单一信号或者其值小于预先设定值时,分解完成。最终原始信号是所有IMF及残余量之和

式中:Ci为本征模态函数;rn为残余量。2.3 Hilbert变换
对所有IMF进行Hilbert变换,则
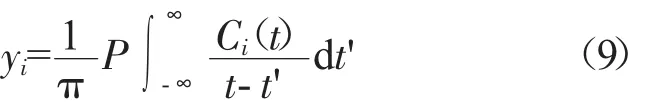
式中:P为柯西主值。
通过Hilbert变换,Ci(t)和yi(t)可以组成解析信号Zi(t),即
其中
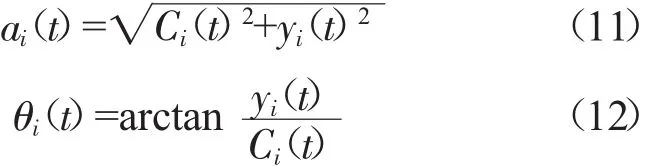
相应可以得到瞬时频率

显然可知

这里省略了残余函数rn,Re表示取实部。展开式(14)称为Hilbert幅值谱,记为
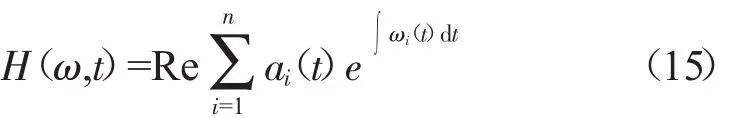
这样可以得到瞬时频率和幅值,可以在时间频率平面上根据幅值的强弱绘制时频谱图。如将其沿时域进行积分,可以进一步定义边际谱
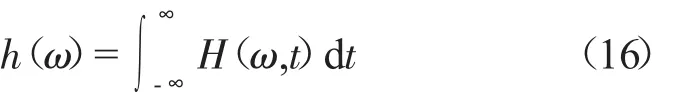
类似傅里叶变换得到的幅频谱,边际谱显示信号能量在频域内的分布,但它们的物理意义完全不同。
2.4 HHT的特点
作为新发展的1种时频分析方法,HHT便于理解、掌握和使用。首先区别于其他方法,它具有自适应性,EMD根据信号的自身特点,直接从信号本身出发对信号进行分解,自适应地将信号分解成数目有限的IMF分量。与短时傅里叶变换相比,它能从时域频域2方面分析信号的局部特征。与小波变换相比,它没有小波基的选择问题,无需根据信号特点选择小波基。
另外,HHT具有良好的时频聚集性。由EMD方法将复杂信号分解成单分量信号IMF后,对各IMF再进行Hilbert变换。通过对解析信号的相位函数进行微分运算来获得瞬时频率,最后得到Hilbert谱。在Hilbert变换时,积分运算不是全局性的,而是通过与1/t进行卷积,使得它的结果相当的局部化。因此,HHT具备良好的时频局部化特性,或者说具有了良好的时频聚集性。
2.5 HHT存在的缺陷
作为1种新兴的信号分析方法,HHT在理论上还有不成熟的地方。
(1)模态混叠。所谓模态混叠就是1个IMF分量包括了尺度差异较大的信号。产生模态混叠的原因是由某1或某几个时间尺度的IMF不连续造成的。而且EMD分解会产生一些低频的与原信号相关性较弱的IMF,这些IMF会在Hilbert谱刻画中产生某些虚假的频率分量。对此,一些研究提出了某些解决方法,2003年Rilling[5]提出了局部EMD方法;2005年Ryan Deering[6]提出了掩膜信号法等。这些方法虽然在一定程度上改善了分解结果,但模态混叠对分析结果的影响仍很严重,特别是频率信息复杂的信号更为突出,是目前制约HHT发展的瓶颈。要想从根本上解决,还要从理论上入手。
(2)端点效应问题。在对原始数据取包络时,需要对上极点和下极点进行样条插值拟合,然后再平均,在进行样条插值时,除非数据的2个端点处就是数据的极值点,否则就会产生拟合误差。在EMD筛选过程中,由于端点处极值的不确定性导致误差的不断向下积累,以此类推,随着分解的进行,误差就会由端点向内逐渐传播,污染内部数据。目前,有些方法试图来改善端效应对分析结果的影响,比如使用比较多的极值延拓法,边界局部特征延拓法,镜像延拓法等,但这些方法只能在一定程度上降低或改善端效应对分析结果的影响,不能从根本上消除。
(3)曲线拟合问题。HHT首先通过极值点拟合信号包络线,再通过EMD方法筛选IMF,这里就涉及到插值拟合问题。HHT提出使用3次样条插值法虽然具有良好的光滑性,但也容易造成过冲和欠冲。因此后续研究者相继提出了不少的修整和改进。比如高次样条插值法、多项式拟合法、阿克玛插值法等。
3 基于Labview的HHT实现
Labview是由美国NI公司开发的在业界领先的工业标准图形化编程工具,主要用于开发测试、测量和控制系统。它将软件和各种不同的测量仪器硬件及计算机集成在一起,建立虚拟仪器系统,形成用户自定义的解决方案[7]。
基于Labview直观易学、接近人类思维、无需编写繁琐代码的特点,本文将上述HHT算法在Labview平台上实现。系统的程序流程如图1所示。
直接利用EMD方法分析计算远远不够,还要考虑到EMD方法造成的端点效应和模态混叠等问题[8]。本程序采用对称延拓法来消除端点效应[9],为了抑制模态混叠和减少虚假IMF分量个数,本程序还要对每次迭代过程的极值点个数及距离等进行控制和有限插值[10]。
4 仿真信号试验验证
现利用某一典型的线性调频信号sin 2π·(10+40·t)·t和1个正弦信号sin 2π·100·t,t∈[0s,1s]相叠加,采样频率为2 kHz,采样长度为1 s。对HHT算法程序的EMD分解和时频分析可靠性进行检验。显然,此叠加信号的频率变化范围在10~50 Hz,同时还有1个频率为100 Hz的正弦信号。仿真信号如图2所示。
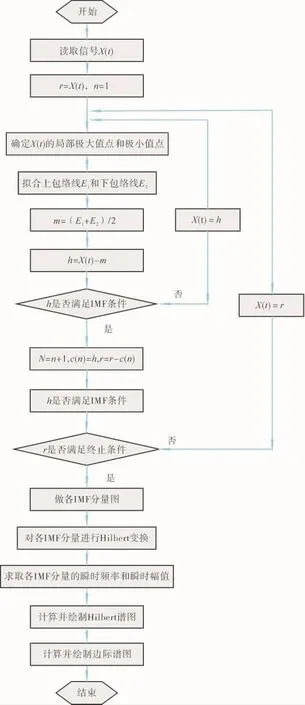
图1 Labview平台实现的HHT程序流程

图2 仿真叠加信号
经过HHT算法程序得到的仿真信号Hilbert时频谱如图3所示。图中曲线颜色的深浅代表幅值的强弱。与图3的傅里叶变换结果相比,HHT将原始仿真信号的频率和幅值随时间的变化规律同时显示在时频谱中。而傅里叶变换(如图4所示)只能单纯给出频域特征,不能同时给出时间和频率的联合信息,对非线性、非平稳类信号无能为力。
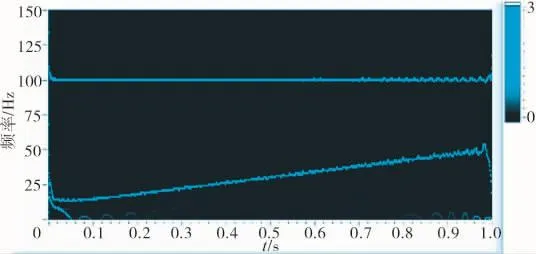
图3 仿真信号经HHT得到的时频谱
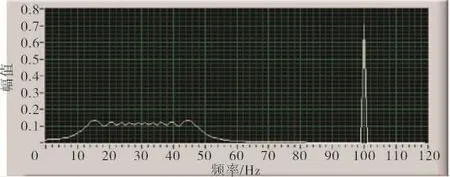
图4 仿真信号的傅里叶变换幅频谱
5 某型发动机气动失稳数据时频分析
目前,HHT已经开始应用于航空发动机气动不稳定性研究,如发动机或压气机试验的旋转失速和喘振、动态畸变试验和压气机转子性能等。
某型发动机台架试车时出现的气动失稳信号如图5所示。对其进行普通的傅里叶变换,如图6所示。
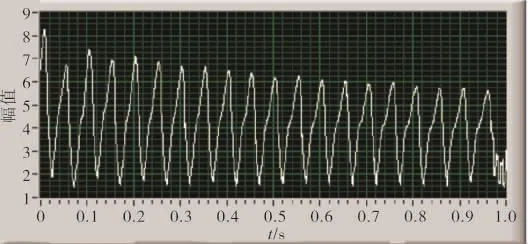
图5 某型发动机台架试车时出现的气动失稳仿真信号
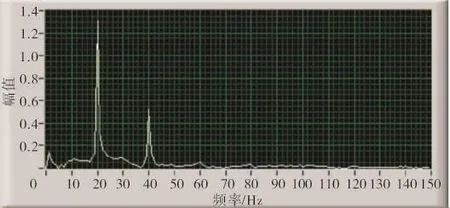
图6 气动失稳仿真信号的傅里叶幅频谱
在除去直流分量,只保留交流分量的傅里叶幅频谱上可观察到,信号主要含有20 Hz和40 Hz 2个频率分量,由傅里叶变换的特点,2个频率分量出现的时间点不得而知。
现采用EMD方法对原始信号进行分解。一共分解出7个经验模态函数(IMF),这里略去后面几个趋于直流的IMF分量,只给出前3个IMF分量,如图7所示,并做出Hilbert时频谱如图8所示。
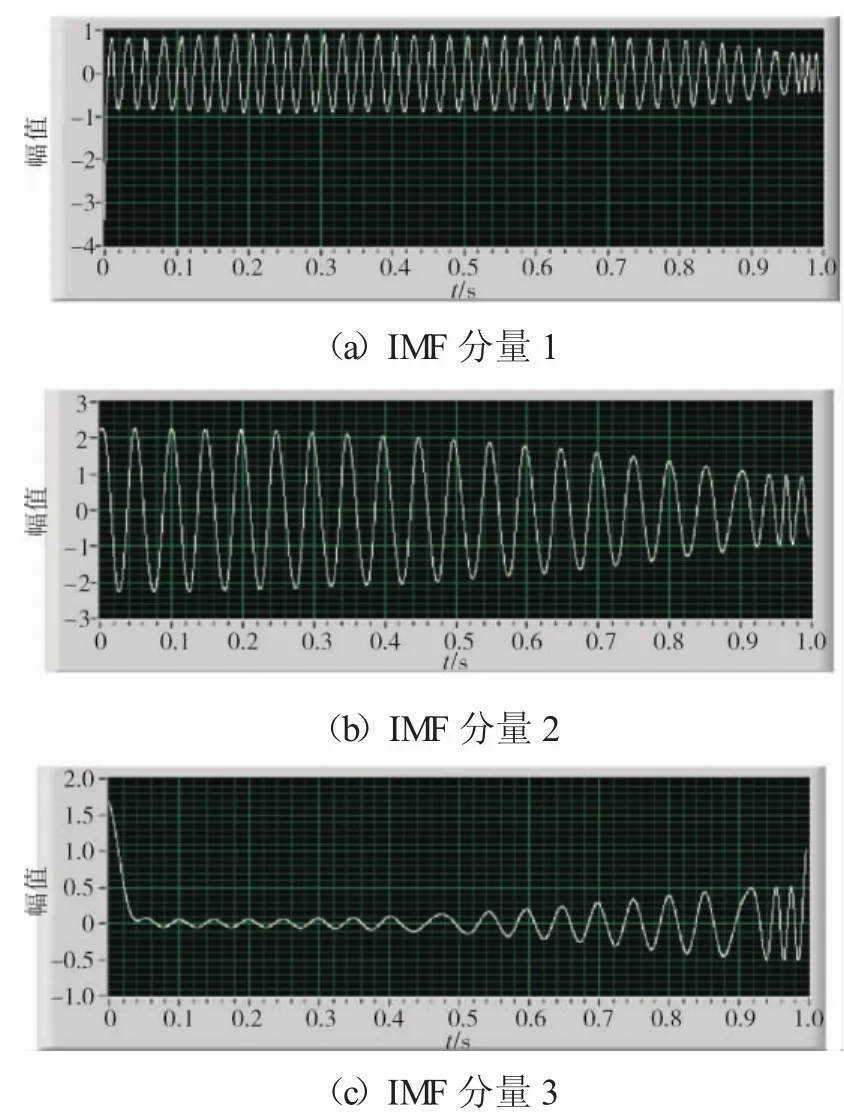
图7 EMD方法得到的IMF分量
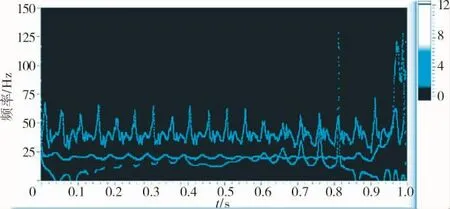
图8 气动失稳仿真信号的Hilbert时频谱
从图8中可见,此气动失稳仿真信号包含的20Hz和40 Hz 2个主要频率分量,基本上同时出现,并贯穿整个信号始终,在信号的结尾0.92 s处开始出现较高频分量,这从EMD分解的几个IMF结果中也可以看出。根据EMD分解性质,各个IMF分量的局部频率依次降低。本次分解结果的IMF1基本上是40 Hz的频率分量,在0.92 s处开始过渡到较高频分量;同样在IMF2中基本上是20 Hz的频率分量,在0.92 s处开始过渡到40 Hz的频率分量;在IMF3以后的分量中信号的直流成分开始占主导。
在信号的起止端,由于数据的截断造成了时频谱的端点效应问题(又称端点飞翼),所以时频谱图在时间起点和终点处的分析结果不准确,如果要求分析此处数据,可以适当延长被分析数据的长度。另外,图中各频率分量抖动的部分是由HHT固有的模态混叠造成,可以通过极值加密、EEMD法、改进掩膜信号法等得到改善,但是基于HHT的实际应用超前理论的研究和发展,若不从理论算法上改进完善,这些问题是不能从根本上得到解决。
6 结论
(1)运用图形化编程语言Labview编制HHT算法,开发过程更加简捷,程序界面更加友好。在运行时间上与Matlab程序相比获得了性能提升,这源于Labview程序所具有的并行特性。
(2)使用HHT方法,定位出不同频率分量在信号中出现的不同时刻,为气动失稳这种非平稳、非线性信号的分析探索出新的途径,同时还验证了HHT的一些优势和不足。
(3)针对使用这种新型的信号时频分析技术处理实际信号时,HHT存在的固有问题[11],本文采取了一些有效措施。
(4)HHT摆脱了传统的傅里叶分析的局限,是一种简单易行,且有效的信号分析方法。将HHT变换应用在发动机气动失稳信号的分析具有适用性。但HHT是新兴的时频分析方法,有待进一步研究和改进。
[1]管霖,吴国沛,黄雯莹.小波变换在电力设备故障诊断中的应用研究[J].中国电机工程学报,2000,20(10):46-49.
GUAN Lin,WU Guopei,HUANG Wenying.Studies on the application of wavelet transform in fault diagnosis of electric devices[J].Journal of Chinese Electrical Engineering Science, 2000,20(10):46-49.(in Chinese)
[2]彭志科,何永勇,卢青.用小波时频分析方法研究发电机碰摩故障特征[J].中国电机工程学报,2003,23(5):75-79.
PENG Zhike,HE Yongqing,LU Qing.Using wavelet method to analyze fault features of rubrotor in Generator[J].Journal of Chinese Electrical Engineering Science,2003,23(5):75-79. (in Chinese)
[3]Choi A.Real-time fundamental frequency estimation by least-square fitting[J].IEEE Trans.Speech Audio Processing,1997(5):201-205.
[4]HUANGDaji,ZHAOJinping,SUJilan.Pracitical implementation of Hilbert-Huang Transform algorithm[J].Acta Oceanologica Sinica,2003,22(1):1-14.
[5]Rilling D,Flandrin P,Gonc P,et al.On empirical mode decomposition and its algorithms[C]//Grado,Italy:IEEE,2003:1-5.
[6]Ryan D,James F K.The use of amasking signal to improve empiricalmode decomposition[C]//Philadelphia:International Conference on Acoustics Speech,and Signal Processing(ICA SSP),2005:485-488.
[7]陈锡辉,张银鸿.Labview程序设计从入门到精通[M].北京:清华大学出版社,2007:1-3.
CHEN Xihui,Zhang Yinhong.Labview Program design junior to superior[M].Beijing:Tsinghua University Publishing House, 2007:1-3.(in Chinese)
[8]胡维平,莫家玲,杜明辉.经验模态分解中的频域分辨率及其改进法[J].华南理工大学学报,2007(5):2-3.
HU Weiping,MO Jialing,Du Minghui.Method for improving frequency resolution of empirical mode decomposition[J].Journal of South China University of Technology,2007(5):2-3.(in Chinese)
[9]陈忠,郑时雄.EMD信号分析方法边缘效应的分析[J].数据采集与处理,2003,18(1):2-3.
CHEN Zhong,ZHENG Shixiong.Analysis on end effects of EMD method[J].Journal of Data Acquisition and Processing, 2003,18(1):2-3.(in Chinese)
[10]毛炜,金荣洪,耿军平.一种基于改进Hilbert-Huang变换的非平稳信号时频分析法及其应用[J].上海交通大学学报,2006(5):1-2.
MAOWei,JIN Ronghong,GENG Junping.A time-friquency analysis for non-stationary signals based on improved Hilbert-Huang Transform and it's application[J].Journal of ShangHai JiaoTong University,2006(5):1-2.(in Chinese)
[11]于德介,程军圣,杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京:科学出版社,2006:46-51.
YU Dejie,CHENG Junsheng,YANG Yu.Hilbert-Huang Transform method formechanical fault diagnosis[M].Beijing: Science Publishing House,2006:46-51.(in Chinese)
Time-frequency Analysis Method of Aeroengine Aerodynam ic Instability Signal Based on Hilbert-Huang Transform
GUO Gui-xi,WANG Zhen-hua,WANG Hong-xiang,GAO Hui-guo, XUEXiu-sheng
(AVIC Shenyang Engine Design and Research Institute,Shenyang 110015,China)
Aiming at aerodynamic instability in aeroengine work scope,the time varying signal characteristics were analyzed by Hilbert-Huang Transform(HHT).The analysis new method of nonlinear and non-stationary signal was compared with other timefrequency analysis methods.The problems of HHT were solved to adapt the data analysis requirements of aeroengine aerodynamic instability.HHT method was implemented and verified on Labview platform by the numerical simulation test.The results show the method is accurate and effective and the project test data processing of aeroengine is presented.The HHT is feasibility and adaptability to solve relative problems.There are some little defection for HHTmethod also.
time-frequency analysis;Hilbert-Huang Transform;aeroengine;aerodynamic instability

2012-12-12
郭贵喜(1980),男,硕士,工程师,从事航空发动机测试工作。
