电阻法测量绕组温升数据处理的方法及应用

韩强 黄柱锋 陈镜亮

（东莞出入境检验检疫局 广东东莞 523071）

1 引言

温升试验是家用电器、变压器、电动工具等电子电器产品的重要检测项目，是测定电器产品在规定条件下，例如：接线端子、外壳、触头、手柄、绕组等零部件的发热温度与环境温度的差值，是否符合相应标准规定的温升限值的检测项目；是评价产品元气件、绝缘材料部件质量，考核电器产品防止火焰蔓延、防止灼伤以及整体电气安全，以及是否对使用者或周围环境产生危险的关键项目。

在对绕组进行的温升试验中，常用的测量温度或温升的方法，除了电阻测温法之外，还有红外线测温法，热电偶测温法。但是，热电偶法、红外线法都局限于被测样品的表面，以及由于测温点选定的随机性，不能真实的反应内部温度；电阻测温法由于其准确度高，可以通过计算得到线圈内部的温度而广泛应用。

2 电阻法测量温度的基本原理

电阻法是根据铜、铝等金属其电阻随温度变化呈现某一规律的特性，通过绕组在发热时电阻的变化，来计算绕组的温度。具体方法是利用绕组的直流电阻，在温度升高后电阻值相应增大的关系来确定线圈的温度，其测得是绕组温度的平均值。在一定的温度范围内，变压器绕组的电阻值将随着温度的上升而相应的增加，而且其阻值与温度之间存在着一定的函数关系。

绕组的温升值按照以下公式计算：

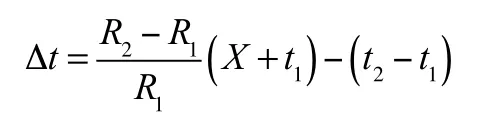
式中：

△t——高于t 的温升，最高温度为△t+t；

R——在环境温度为t时，试验开始时的绕组电阻，单位是欧姆；

R——当达到稳定状态时，试验结束时的绕组电阻，单位是欧姆；

X——对于铜线绕组为234.5，对于铝线绕组为225；

t——试验开始时的环境温度，单位是摄氏度；

t 试验结束时的环境温度，单位是摄氏度；

试验开始时，绕组的温度应等于环境温度。

冷态时的电阻R (试验开始测得的电阻)和热态时的电阻R (试验结束测得的电阻)必须在被测绕组同一出线端测得。

要精确测量线圈电阻，只能使用高精度的数字电桥。而数字电桥只能在被测绕组断电的环境下才能开展测量，它对电流非常敏感，绕组从电源断开后还需短路几秒钟(实际操作一般是5秒)再接到电桥上测电阻，以避免残余电量烧坏电桥。

由于这个原因，我们没办法得到绕组断电瞬间To时的线圈电阻值R ，因此，只能通过间接的方法来得出R ，即根据绕组导体电阻随温度变化呈现某一规律的特性，推算出断电瞬时的电阻值R ，就可推算出线圈温升△t。绕组断开电源后，其温度逐渐下降，所以测得的电阻值并不是线圈断电瞬时的电阻值，我们可以通过短时间等间隔读取的电阻测量值，利用作图法和回归分析法来确定断电瞬时的电阻值，从而推算出绕组温升。

3 绕组断电瞬时的电阻值R的确定

确定断电瞬时的电阻值R一般有两种方法：作图法和回归分析法。

3.1 作图法

作图法是在直角坐标系上画出“电阻—时间”的相关曲线，然后通过相关曲线来确定断电瞬时的电阻值R 。为了能准确绘制电阻与时间变化的曲线，测量次数应在10次左右，而且第一个测量值越快，测试准确度越高，作图法比较直观。用作图法处理数据时，我们通常采用的是“目测法”，这种方法虽然简单明了，易学易用，但常常受人为因素影响较大，即使对同一组数据来说，不同的人员也会得出不同的结果来。因此， 该方法只在进行快速估算的情况下使用。对于检测实验室，不推荐使用此种方法。

3.2 回归分析法

所谓回归分析法，是在掌握大量观察数据的基础上，利用数理统计方法建立因变量与自变量之间的回归关系函数表达式（称回归方程式）。

具体在电阻法测量绕组温升的实际应用中，是根据多次测量的绕组断电后时间及与其对应的绕组电阻值，再结合一些数理统计方面的知识，运用回归分析的方法，在数学上严格地确定电阻与时间的相关曲线，最后找出断电零时刻的电阻值。

在回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。此外，回归分析中，又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析。通常线性回归分析法是最基本的分析方法，遇到非线性回归问题可以借助数学手段化为线性回归问题处理。

3.2.1 一元线性回归方程

一般地，用线性函数a+bx来估计Y的数学期望的问题，称为一元线性回归问题。称方程

为Y的关于x的线性回归方程。称斜率b为回归系数。对于x的每个值，设：

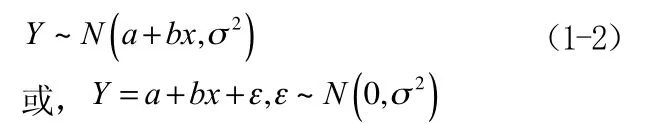
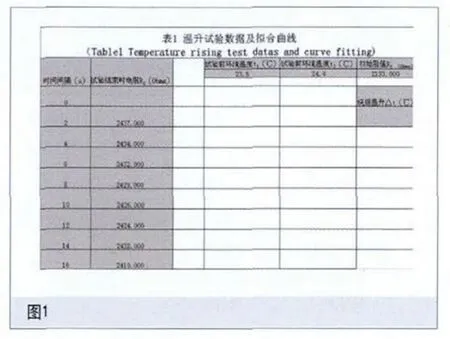
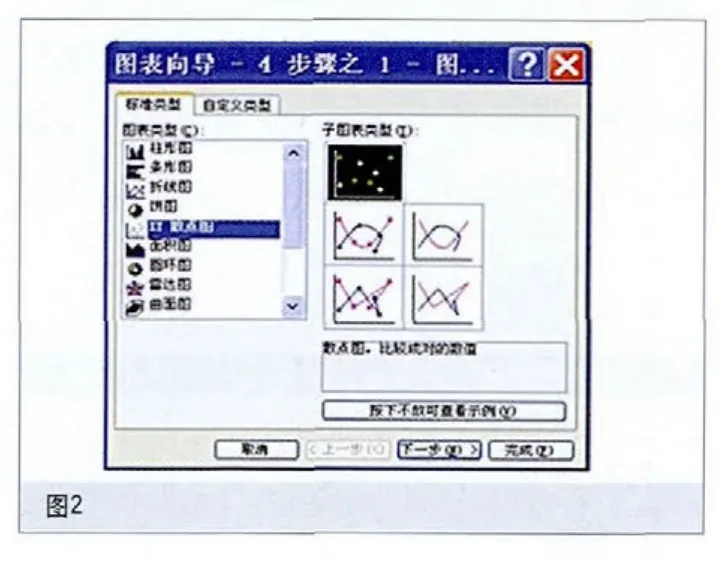
其中a,b,σ是与x无关的常数。对于已知数据(x,y) (i=1,2,…,n) ，用最小二乘法来估计a和b，离差平方和：

为了使Q取得最小值，将Q分别对a和b求偏导数，并令它们等于零，得

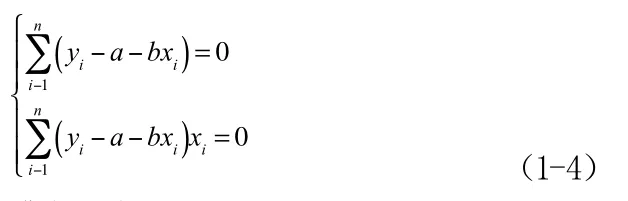
或者写成

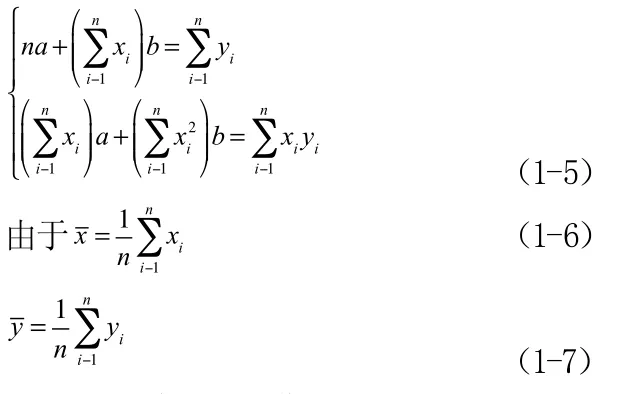
则（1－5）式可以写作

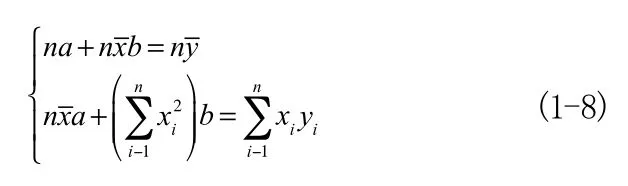
方程组（1-8）称为正规方程组，该方程组有唯一的一组解

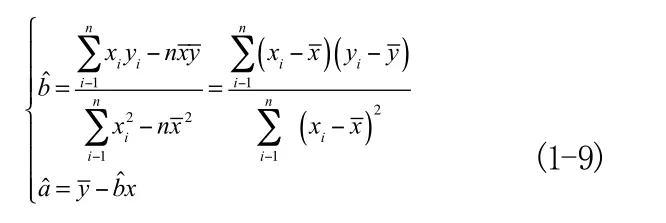
记:

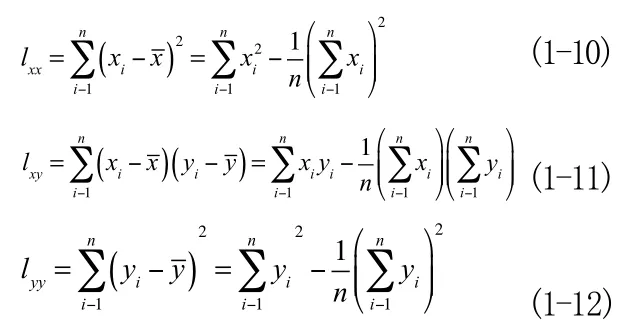
分别成l 和l 为x和Y的离差平方和，称l 为x和Y的离差乘积和。则有

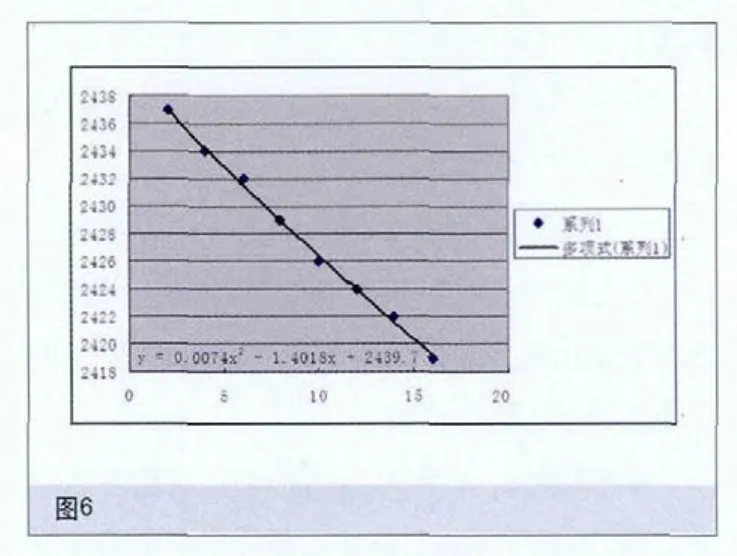
将（1－13）代入到回归方程（1-1）中,则得到经验回归方程

3.2.2 一元非线性回归方程

上节讨论的回归分析与回归模型都假定是线性的，而在使用“电阻法测温升”通过作图法发现测得的数据并不是线性分布的，因此，为了得到准确的数据，我们需要建立的一元多次非线性回归模型。由于线性回归方程比较简单，所以在遇到非线性模型时，最好将其转换为线性模型。

由此可见，求一元多次的多项式回归的问题就转化为多元线性回归模型。具体可参考相关数学书籍。通过实践证明，一元多次回归求出的R值比一元一次回归要更接近真实值，而且次数越高，数值越精确。为了减少计算量，在满足试验精度要求的情况下，一般推荐使用一元二次方程来求R值。

4 Excel软件在数据处理中的应用

随着计算机应用日益普及，用Excel软件处理实验数据已经逐步推广。Excel软件在实验数据曲线(直线)方程拟合、作图、计算公式值和常用函数值、计算测量列平均值、标准偏差和不确定度等都有独特的功能。利用Excel软件图表功能可以很方便对实验数据作图,并对测量点添加趋势线,得拟合曲线函数关系式，实现对检测数据的回归分析。

下面就介绍一下利用Excel的绘制散点图功能，对数据进行曲线拟合及生成该组数据函数方程的过程。假定在变压器温升试验中获得表1数据。

(1)根据上组数据新建一张Excel数据表，输入试验数据，并选中，如图1。

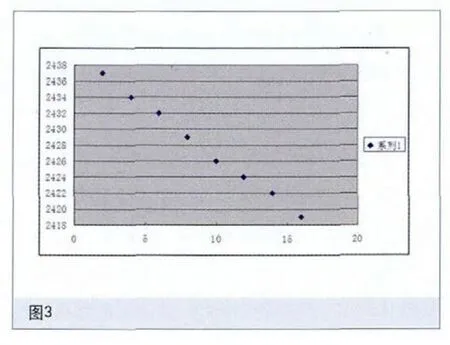
(2)在“插入”栏中选择“图表”，屏幕上显示如图2所示的”图表向导”，然后选“XY散点图”连续按下一步，完成“图表向导”4步骤。在表格中就会显示如图3所示的曲线图。

(3)在所得的曲线上击右键，选中“添加趋势线” 然后如图4所示，在“类型”框中选择“多项式”，并在“阶数“栏中确定阶数，在满足试验精度要求的情况下，一般设定为2阶。

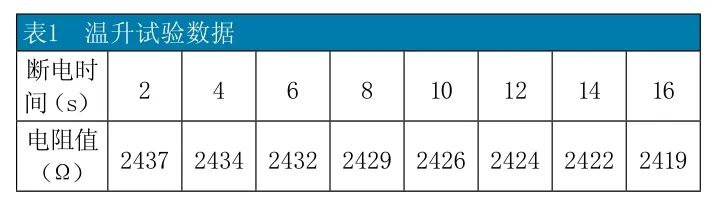
表1 温升试验数据断电时间（s） 2 4 6 8 10 12 14 16电阻值（Ω） 2437 2434 2432 2429 2426 2424 2422 2419

(4)在“添加趋势线“的”选项“框中，选中”显示公式“(图5)，再按确定，曲线拟合就完成了，拟合好的公式图6所示，显示在曲线图图6上。

(5)根据显示的公式

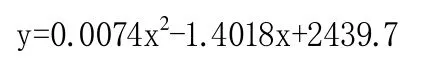
可计算出当断电瞬间T=0s即x=0时，绕组电阻y=2439.7Ω。

5 结束语

由此可见，电阻法测量绕组温升的方法和精度都会对产品的合格性评定产生决定性的影响，很多产品都会因为在涉及温升的测试中出现问题。利用Excel的可绘制散点图的功能，实现对检测数据的曲线拟合，数据处理准确、直观、快捷、简易。

[1]谢秀杰.电阻法测温的原理及数学计算[J].电子质量.2008年第12期

[2]张红飚.电阻变化法测量绕组温升的探讨[J].福建分析测试.2005年第3期

[3]IEC61558-1:2005+A1:2009，Safety of power transformers, power supplies, reactors and similar products Part 1: General requirements and tests [S].

[4]GB 19212.1-2008, 电力变压器、电源装置和类似产品的安全 第1部分：通用要求[S].

[5]何晓群，刘文卿.《应用回归分析》第二版[S].

[6]盛骤等.《概率论与数理统计》[S].