基于模糊滤波算法的时滞系统温度控制及误差补偿
2013-07-07赵尉麒蔡锦达
赵尉麒, 蔡锦达
(上海理工大学机械工程学院,上海 200093)
基于模糊滤波算法的时滞系统温度控制及误差补偿
赵尉麒, 蔡锦达
(上海理工大学机械工程学院,上海 200093)
利用自适应滤波算法调整模糊控制的输出,可解决大时滞温控系统的稳态振荡问题,但无法消除系统稳态误差.提出新的误差补偿算法,可以进一步消除稳态误差,减小参数整定工作量.将其应用于全自动化学发光免疫分析仪的试剂仓恒温控制.仿真结果表明,该算法能使大时滞温控系统得到稳定控制并增强系统的自适应能力和鲁棒性.
模糊控制;LMS自适应滤波器;温度控制;时滞系统;误差补偿;PI控制器
在全自动化学发光免疫分析仪的设计中,试剂存储仓的温度控制是一个关键技术.在工程中PID(比例-积分-微分控制)算法常被用作温度控制,传统PID算法在对非线性或时变系统的控制中通常不能取得较好的效果[1-3].由于免疫分析仪是一个较大的系统,结构复杂、控制部件繁多,准确获取系统控温部分传递函数是十分困难的.加之试剂储量、工作环境等都会对系统传递函数产生影响,因此,使用传统PID算法控制效果通常不好.与传统PID算法相比,采用模糊控制算法不需要系统的传递函数,可以解决以上矛盾.但试剂存贮仓是一个大时滞系统,由于时滞的存在,控制曲线通常会在目标温度值附近不断振荡.本文提出新的控制方式能够解决复杂带时滞系统的控制难题.使用模糊算法对温度进行控制,通过LMS(最小均方算法)自适应滤波器消除时滞带来的系统振荡.使用PI(比例-积分)控制器解决通过自适应滤波器后的稳态误差问题.本文应用Matlab软件对该算法进行了仿真研究.
1 LMS模糊温度控制器设计
1.1 系统结构
图1为系统控制框图.图中,d u/d t为微分模块,1/s为积分模块,k1,k2,k3为输入输出量的比例因子,C1,C2,C3为经过控制器后的3个控制量.通过实时温度采集并与设定温度比较,得到温度误差e与误差的变化率Δe,将其分别用于模糊控制器、LMS自适应滤波器和PI控制器的输入.系统总输出表示此时控制量输出的强度,将其转化为脉冲宽度调制(PWM)信号,可用于实际控制中.Kp为比例系数.
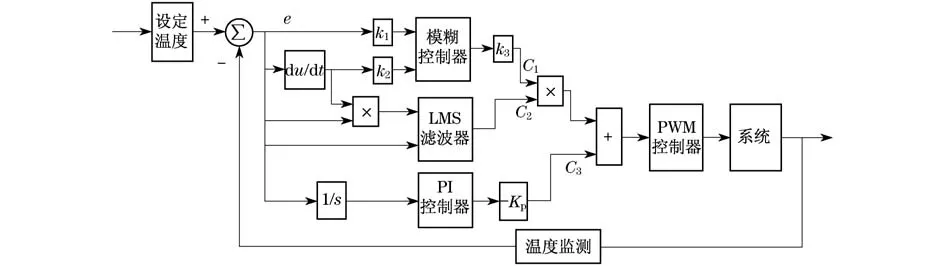
图1 系统控制框图Fig.1 System control diagram
1.2 模糊温度控制器设计
模糊控制作为一种人工智能手段,将输入量按一定的模糊控制规则自动进行推理运算,模仿专家经验,从而获取问题的求解,在处理不确定性和不精确性问题时具有良好的鲁棒性[4].
温控系统采用半导体制冷片进行温度控制,被控量为温度.通过实时采集系统当前温度t(i),并与目标温度比较,可以得到模糊控制器的2个输入量

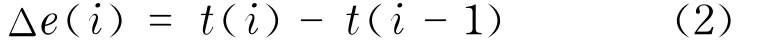
式中,T为目标温度;t(i)为i时刻温度;t(i-1)为i-1时刻温度;e(i)为i时刻温度误差;Δe(i)为i时刻温度误差变化率.
误差e(i)与误差的变化率Δe(i)采用三角形隶属函数,2个输入量论域均设为-2≤t≤2,输出变量的论域设为-10≤t≤10,如图2所示.输入输出变量取语言值{NB,NS,Z,PS,PB}.模糊化规则表如表1所示(见下页).
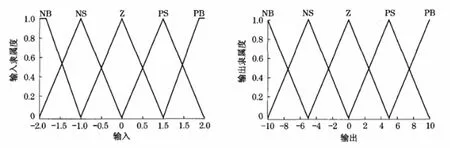
图2 输入输出变量隶属度函数Fig.2 Membership functions of input/output variable
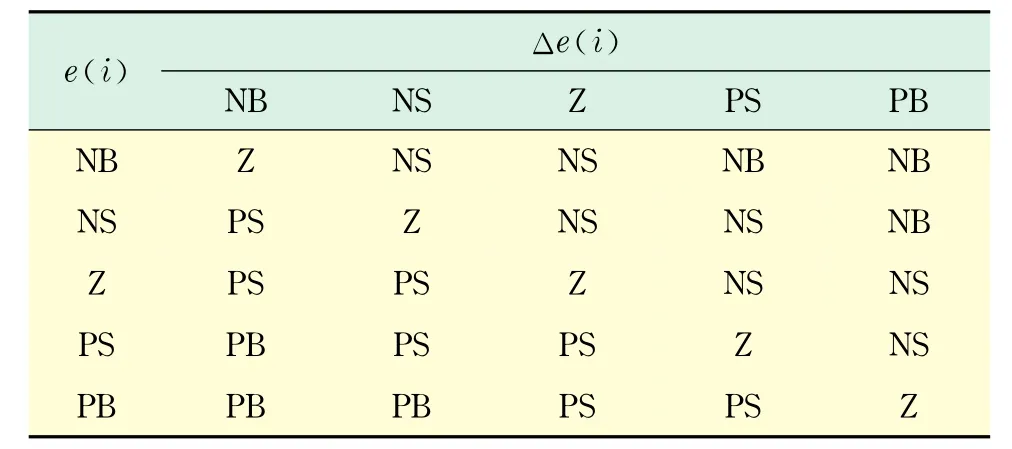
表1 模糊化规则表Tab.1 The fuzzy rule table
模糊控制器的推理过程采用Mamdani算法,使用重心法解模糊.输出结果作为控制量C1.
1.3 LMS自适应滤波器的引入
由于试剂仓的温度控制系统中被控对象带有时滞环节,采用普通模糊控制算法采集到的温度参数通常不是当前值,因此会给系统带来超调与稳态振荡.LMS滤波算法由Widrow和Hoff首先提出,由于其结构简单、计算量小、稳定性好成为目前应用最广泛的自适应滤波算法[5].该算法可以根据系统变化实时调整权系数,使得输出满足期望.带时滞系统的模糊控制曲线会在目标虚线附近不断振荡.根据温度响应曲线绘制相平面特性曲线,如图3所示.
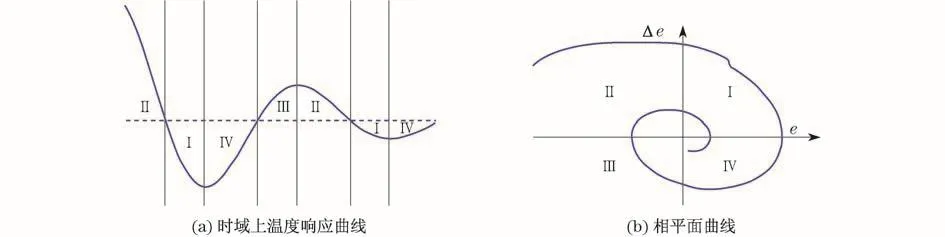
图3 温度控制相平面曲线Fig.3 Phase plane curve of temperature control
在I、III象限均有e·Δe>0,II、IV象限均有e·Δe<0.e·Δe>0时,温度响应曲线应向虚线逼近,即减小控制量.e·Δe<0时,温度响应曲线应远离虚线方向,即增大控制量.因此,温度误差e和误差的变化率Δe的乘积可以反应被控对象的动态变化情况[6].LMS滤波器的权值w会随着输入量与期望值的变化而更新.此处取温度误差e作为LMS滤波器的误差输入[6].通过将滤波器输出量与模糊控制器输出量相乘来对控制量的强度进行控制.
设计滤波器迭代算法为
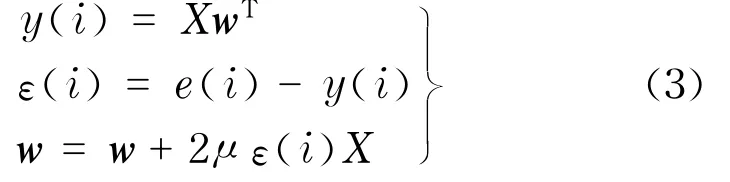
式中,X为温度误差e和误差的变化率Δe点积的序列;i为迭代次数;ε(i)为误差信号;μ为迭代步长;w为权值.
设滤波器长度为L,
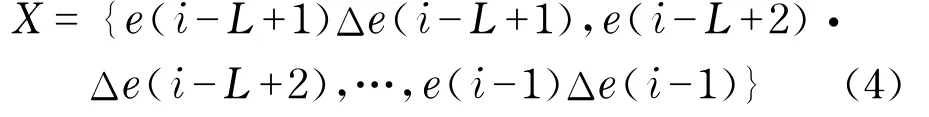
输出结果y(i)作为控制量C2.
实验证明,引入LMS自适应滤波器后,因时滞产生的系统稳态振荡消失了.如图4所示.但是,由于模糊控制的控制作用较粗糙,输出是根据偏差和偏差的变化进行推理得到的,本质上属于PD(比例微分)控制,无法消除系统稳态误差[7].虽然可以通过增加模糊规则、增加模糊控制器输入量的方式提高系统控制精度,但这都会使得模糊控制算法的复杂度急速增加.同时也会增加模糊控制器的设计难度.

图4 闭环LMS自适应滤波器Fig.4 Closed-loop LMS adaptive filter
1.4 稳态误差的消除
本文提出在基于LMS的模糊控制器后加入PI比例环节,可去除稳态误差,使误差能够在一定的迭代次数后趋于理想值.
具体做法是采集系统当前时刻之前的L个时刻的温度误差值(L为滤波器长度),对其求和并乘以比例系数Kp,将其作为控制量的一部分.
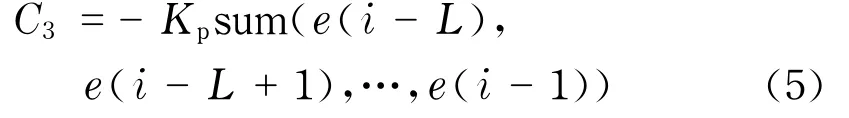
比例系数Kp取一个正数,即实际温度高于设定温度时加大控制量,实际温度小于设定温度时减小控制量.通过仿真实验证明,采用此方法可以有效去除稳态误差.虽然加入积分环节会带来系统的振荡,但振荡总能较快地收敛.调节Kp参数可以消除振荡,Kp绝对值的大小用于控制PI控制器的控制强度.相比仅使用LMS自适应算法的模糊控制器更易操控,消除了系统的稳态误差.即使控制系统的时滞、响应时间在一个小范围变化时也能自行调整,保证实际温度达到设定值.
2 仿真结果及分析
模糊算法与自适应滤波算法均不需要精确的系统模型即可实现对系统的控制.由于系统主要受大惯量和时滞影响,为了对系统仿真,可假设系统满足一阶数学模型
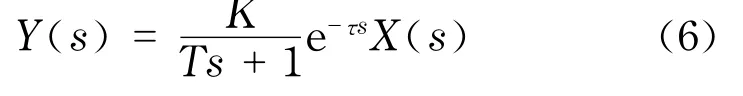
式中,K为阶跃响应稳态增益;T为响应时间;τ为时延因子.
仿真过程中选取K=-27,T=180,τ=100.
图5为仅使用模糊控制得到的结果,可以看出,由于系统时滞的存在,采集到的温度不是实时的,即在系统达到目标温度后,由于采集到的温度是滞后的,认为系统还未达到目标温度,因此会继续加大控制量,最终使得系统在目标值附近不断振荡,无法收敛于目标值.如图6所示,加入自适应LMS滤波器后振荡得到了控制,温度曲线在目标值5℃附近趋于稳定.仿真实验表明,通过调整LMS滤波器的收敛步长可以曲线逼近目标值,但在现场调试中这种调整耗时且无法做到准确.在系统正常工作中,试剂存储仓内存放物质的量、环境温度都会对系统的传递函数造成改变.另外,受环境因素的影响,会导致传递函数的改变.这对温度最终收敛值亦会有较大影响,因此,需要加入误差补偿.加入PI控制器后,可保证系统温度实时自适应地收敛于目标值.仿真实验中选取Kp= 0.02.
如图7所示,在加入PI控制器后系统能够趋于稳态且消除了稳态误差.考虑系统工作时环境工况的变化,当响应时间由T=180分别变为T=160与T=200,而其余各项参数不变的情况下,仿真结果如图8所示(见下页).当响应时间由T=160,变为T=200系统仍能趋于设定值.
当时延因子由τ=100分别变为τ=80与τ= 120时,仿真结果如图9所示(见下页).
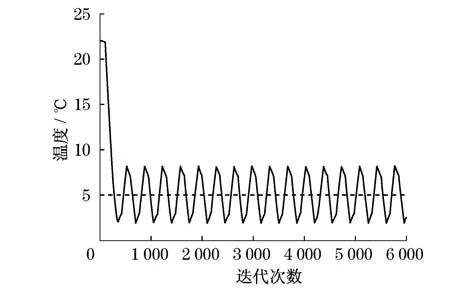
图5 使用普通模糊算法仿真结果Fig.5 Common fuzzy algorithm simulation results
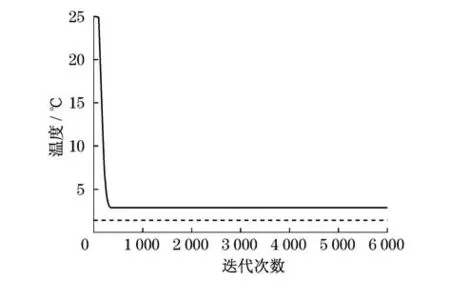
图6 加入滤波器后模糊算法仿真结果Fig.6 Fuzzy-LMS algorithm simulation results
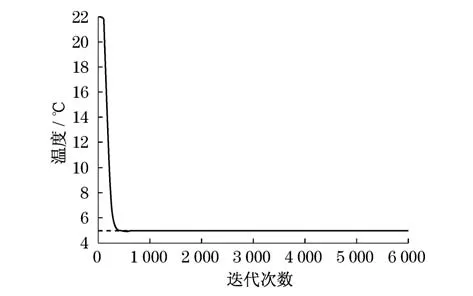
图7 加入PI控制器后仿真结果Fig.7 Fuzzy-LMS algorithm simulation results with PI controller
同样地,延时因子的小幅变化不会对控温效果产生太大影响.因此,该系统具有一定的鲁棒性和自适应性.
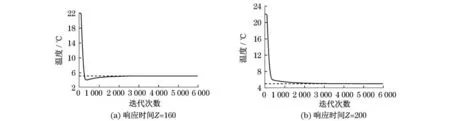
图8 响应时间变化对收敛性能的影响Fig.8 Influence of response time on convergence performance
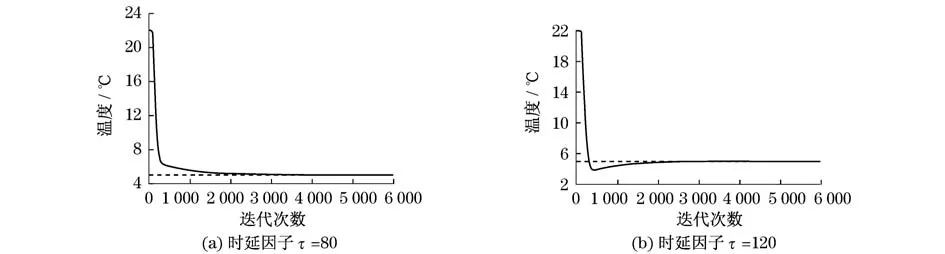
图9 时延因子变化对收敛性能的影响Fig.9 Influence of time-delay factors on convergence performance
3 结束语
使用基于自适应滤波器的模糊控制算法,解决了试剂存储仓的温度控制问题.提出了一种稳态误差补偿算法,采用该算法后可使系统温度稳定到目标值,减少了反复整定系统参数带来的困难.同时,使系统具备了较强的鲁棒性和自适应性.
[1] Petrov M,Ganchev I,Taneva A.Fuzzy PID control of nonlinear plants[C]∥First International IEEESymposium,Intelligent Systems.2002,1:30-35.
[2] Setieo S,Torrey D A.Fuzzy logic control of a space-vector PWM current regulator for three-phase power converters[J].IEEE Transactions on Power Electronics,1998,13(3):419-426.
[3] 段雪涛,邬志敏,王芳,等.基于PID控制的4工位冰箱性能测试试验室研制[J].上海理工大学学报,2005,27(4):327-330.
[4] 李勇,罗隆福,许加柱,等.基于模糊控制的直流电机PWM调速系统[J].大电机技术,2006(1):66-68.
[5] Yan Y G,Zhao J W,Wang Z K,et al.An novel variable step size LMS adaptive filtering algorithm based on hyperbolic tangent function[C]∥2010 International Conference on Computer Application and System Modeling.2010,14:233-236.
[6] 孙桂玲,金镇.基于LMS算法自调整模糊温度控制器的仿真研究[J].系统仿真学报,2006,18(11):3108 -3114.
[7] 徐洪洲,龚磊.一类时滞系统的自校正模糊Smith控制器设计[J].计算机与现代化,2009(8):65-72.
(编辑:石 瑛)
Temperature Control and Error Compensation of Time-Delay System Based on Fuzzy-LMS
ZHAOWei-qi, CAIJin-da
(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
The adaptive filter algorithm was applied to the fuzzy controller.The output of the filter was used to control the influence of fuzzy controller on the system.The filter can remove the steady-state oscillation in the time delay system.But,unfortunately,it brings in the steady-state error.Therefore,an algorithm was proposed to compensate the error and also,to reduce the workload of parameter tuning.The algorithm was designed and used in the automated chemiluminescence immunoassay analyzer.The conclusion indicates that the algorithm can adaptively control the temperature in the time delay system.It is robust to the slight changes in the external environment.
fuzzy control;LMS adaptive filter;temperature control;time delay system;error compensation;PI controller
TP 13
A
1007-6735(2013)03-0240-05
2012-06-25
上海市教委科研创新资助项目(12YZ094)
赵尉麒(1989-),男,硕士研究生.研究方向:智能控制、嵌入式系统开发.E-mail:zhaoweiqi40@126.com
蔡锦达(1963-),男,教授.研究方向:嵌入式系统开发、数控系统设计.E-mail:cjd6309@126.com
