超网络研究
2013-07-07漆玉虎郭进利
漆玉虎, 郭进利,2
(1.上海理工大学管理学院,上海 200093;2.上海理工大学超网络研究中心,上海 200093)
超网络研究
漆玉虎1, 郭进利1,2
(1.上海理工大学管理学院,上海 200093;2.上海理工大学超网络研究中心,上海 200093)
作为研究复杂系统与复杂性问题的新方法,在复杂网络研究成热潮后,超网络研究开始受到关注,并被广泛运用于解决实际问题.为全面探讨超网络研究的现有成果,首先对超网络的基本概念、基本特点和常见模型进行了总结;接着描述了基于变分不等式、基于超图和基于系统科学的研究方法,并对其研究现状分别进行了回顾;随后简述了超网络在网络平衡问题、知识网络表述与鲁棒性研究中的应用,以及超网络统计特性研究;最后,总结了超网络现阶段研究的不足并对今后的研究进行讨论和展望.
超网络;变分不等式;超图;统计特性
人类生活的世界包含形形色色的复杂系统,多数可用网络描述.网络由点集和边集组成:节点代表系统的主体,边代表主体间的联系.根据联系方式的不同,网络可分为有形网络:如计算机网络[1]和神经网络[2],以及无形网络:如病毒传播网络[3]和知识网络[4].可以说人类不仅生活在网络中,而且本身即为网络,其言行举止与网络息息相关,因此网络研究意义深远.18世纪著名数学家欧拉通过对“七桥问题”的建模与分析,提出用图论研究现实网络、解决实际问题的方法.随后300多年,网络研究经历了规则网络[5]、随机网络[6-8]和复杂网络等3个研究阶段,而WS模型[2]与BA模型[9]的建立,更是开辟了网络研究的新纪元.
社会的快速发展,导致现实网络更加复杂,先前的研究方式已无法全面研究现实网络.首先,现实网络多为综合网络,而先前的研究方式多限于研究节点与边同质的网络,无法完全刻画现实网络特征.如电力网络[2]和生态网络[10],前者边不同质,后者节点不同质;而供应链网络[11]则边与节点均不同质.其次,网络研究的目的是为揭示自然规律进而推动社会发展,故对综合网络研究的意义更深远.如研究快递网络[13]可有效提高送货效率和降低运输成本,研究组织知识管理网络[14-15]则可使组织了解自身的知识资源,并开展相关培训.
综上所述,网络研究将进入探讨网络间联系与影响的研究阶段,超网络既可完美刻画现实网络特征,本身又为综合网络,故超网络研究必将成为网络研究新潮流.文章将对超网络的概念、模型、研究方法、研究现状以及实际应用作出简要介绍,并对研究的不足和未来方向进行讨论.
1 超网络概念
现实系统是由多种主体,多种关系组成的复杂系统,在网络中表现为节点与边的不同质性.虽早有人用超网络描述计算机系统和运输系统[16],但研究却并未展开.21世纪初,随着计算机处理技术与运算能力的快速发展,开始有研究者系统研究超网络,并将其用于解决现实问题.目前常见的超网络概念主要有以下几种.
1.1基于图的超网络
基于图的超网络(supernetwork)提出于1985年,当时把规模巨大、连接复杂且网络嵌套网络的大型网络称为超网络[4,16].最早明确提出超网络概念的是美国科学家Nagurney,她在处理物流网络、资金网络和信息网络相交织的问题时,将“高于而又超于现存网络”的网络,用supernetwork来描述[17-19].“高于而又超于”就是网络嵌套网络,且存在虚拟的节点、边和流等的网络[20].
该类超网络含部分以下特征[21]:a.网络嵌套网络:组织知识超网络[4]含知识点、知识主体等网络;b.多层特征:供应链超网络[18]有管理层、物流层等层次;c.多级特征:电力超网络[22]有电厂、用户等级别;d.流量是多维的:生态超网络[23-24]分为物质与能量的流动;e.多属性或多准则:快递超网络[13]有成本最小、时间最短等优化准则;f.存在拥塞性:运输超网络[25]和计算机超网络[26]等有拥塞性;g.全局优化和个体优化需要协调:军事供应链超网络[27](如图1所示)供应链利益优化与民营企业或第三方物流利益优化会产生冲突.
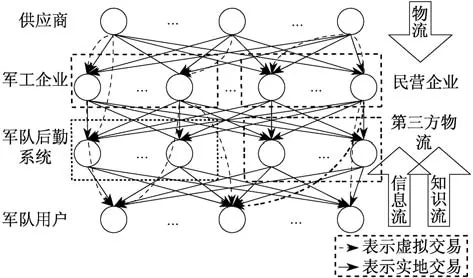
图1 军事供应链超网络模型[27]Fig.1 Military supply chain supernetworks model[27]
基于图的超网络与复杂网络的区别在于:其比复杂网络更复杂,目前研究的复杂网络为节点众多且规模较大的网络,但为研究的准确性,节点与边会保持同质.而基于图的超网络则是由多种节点与边组成,子网内与子网间均连边的节点众多且规模巨大的网络.
1.2 基于超图的超网络
由于复杂网络点与边的同质性,其只能描述两节点间的关系,无法描述多节点间的合作关系.有研究者用二部图弥补此缺陷,但节点类的不同,使得网络特性的研究结果充满歧义[12,23].遂有研究者采用超图理论:以作者为节点,以成果为边集,完美描述了该类网络.在保证节点与边的同质性前提下,又清晰显示作者间关系和成果作者等信息,这就是基于超图的超网络(hypernetwork).
Berge[28]于1970年提出超图的概念,并描述了无向超图理论[29].随后有学者对有向超图理论[30]、超图的超回路、着色和t-设计[31]等进行研究.
定义1 超图[28-29]
设V={v1,v2,…,vn}是有限集.若
a.Ei≠Ø(i=1,2,…,m);
则二元关系H=(E,V)为一个超图,V的元素v1,v2,…,vn为超图的顶点,E={E1,E2,…,Em}为超图的边集,集合Ei={vi1,vi2,…,vij}(i=1,2,…,m;j=1,2,…,n)即为超边.
定义2 对偶超图[32]H*
例1 若某机构有7名科研人员,分别由a1,a2,a3,a4,a5,a6,a7表示;合作完成5项成果,分别由b1,b2,b3,b4,b5表示,成果作者集可表示为:b1(a1,a3,a6),b2(a2,a7),b3(a3,a5,a7),b4(a5,a6),b5(a4),所得二部图、超图和对偶超图分别如图2(a)—(c)所示.该类超网络节点与边分别同质,且节点集与边集各代表一类网络,故其为节点与边同质的综合网络.文献[12,23]认为,凡是可以用超图表示的网络就是超网络,则基于超图的超网络与复杂网络的区别在于:复杂网络的边只连接两个节点,而超图网络的超边是可包含任意数量节点的集合.

图2 例1对应图Fig.2 Graph for example 1
除以上定义外,Frank[33]也给出了自己的理解.关于两种定义的关系,王众托院士认为基于图的超网络包含的网络系统范围比基于超图的超网络更广,即有些超网络是无法用超图描述的.但两者都是“高于而又超于现存网络”的网络,且都只是超网络的子类[34].故认为:a.超图只是研究者研究超网络,刻画现实网络的一种方法,就如Nagurney用变分不等式研究超网络平衡问题一样;b.以上两种概念均无法完全描述超网络系统.
2 超网络模型
2.1 供应链-社会超网络模型
由包含M个生产商、N个供应商和O个需求市场的3层供应链网络与社会网络组成,供应链网络的边代表产品间的交易,社会网络的边代表各层决策者间的关系[17].实边为有形的交易,而虚边为无形的交易,如电子商务等.模型如图3所示.

图3 供应链-社会超网络模型[17]Fig.3 Society-supply chain supernetwork model[17]
2.2 供应链-运输超网络模型
由4层供应链网络与运输网络综合而成[35],包含供应链网络的生产商、供应商、零售商、需求市场与运输网络的货运商.涉及Y种商品,对每种商品y,都有My个生产商、Ny个供应商、Ry个零售商、Uy个货运商及O个需求市场.供应链网络的4层决策者间存在运输关系,故货运商存在于相邻决策者之间,即不同层节点间存在多条边.模型如图4所示.
2.3 化学反应超网络模型
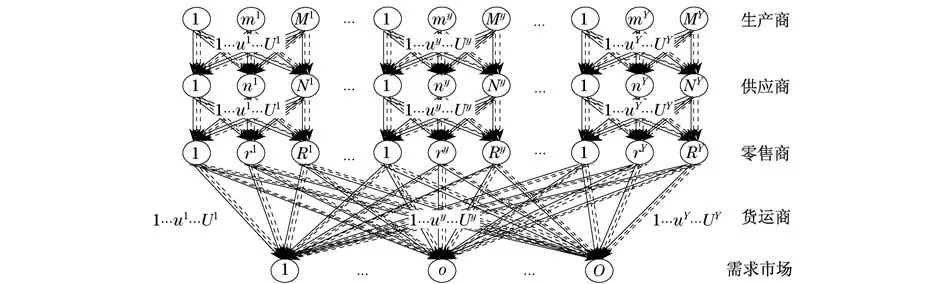
图4 供应链-运输超网络模型[35]Fig.4 Supply chain-transportation supernetwork model[35]
化学反应是几种反应物Gi按比例gi相互作用,得到另外几种比例为gi的反应物Gi的过程[23],可表示为:

基于图的网络(以反应物为节点,以物质是否参与同一反应过程连边)无法清晰描述化学反应过程中涉及到的反应物,而用有向加权超图表示该网络[36]:以反应物为节点,以化学反应过程为有向超边,以反应物比例为超边的权值,可清晰描述所有化学反应过程与反应物间的关系.
2.4 生态超网络模型
生物种群间存在营养关系和竞争关系,先前的生态网络研究以生物种群为节点,种群间的营养关系或竞争关系为边,分别建立食物网和竞争网来研究[10].由于种群间可能既是营养关系,又是竞争关系,故该方法无法全面描述生态网络.而以生物种群为节点,亦以生物种群为超边[24](以该种群为食的种群集合),构建的生态超网络可清晰描述种群间的营养关系与竞争关系.
2.5 其它超网络模型
除以上模型外,还存在其它超网络模型.这些模型有基于图的超网络模型,如组织知识超网络[4]、快递超网络[13]、交通运输超网络[37]和回收超网络[38]等;也有基于超图的超网络模型,如社会超网络[39](以行动者为节点,以过程为超边)、蛋白质超网络[40](以蛋白质为节点,以蛋白质复合物为超边)、新陈代谢超网络[41](以分子实体为节点,以代谢反应为超边)等.
3 研究方法
超网络研究对象所涉及学科和类型的多样化,导致研究方法的多样性.目前可归结为3种:基于变分不等式的研究方法、基于超图的研究方法和基于系统科学的研究方法.
3.1 基于变分不等式的研究方法
为解决机械原理问题与交通平衡问题,Lions等[42]和Daniele等[43]分别提出进化变分不等式和时间独立的进化变分不等式.Nagurney证明所有超网络模型都可转换为有限维的变分不等式问题,并用变分不等式和投影算法解决固定条件下的供应链超网络平衡问题[18].随后她构建条件可变的动态系统,并结合Cojocaru等综合进化变分不等式与Hilbert空间上的投影动力系统,提出解决动态系统的修改后的投影算法[44].目前该方法多用于解决多层、多准则的超网络模型平衡问题.
3.1.1 变分不等式
定义3 变分不等式[17,21]:有限维的变分不等式问题VI(F,K),就是求解向量X*∈K,满足

其中,F是给定的从K到ℝN连续函数;K是闭凸集;〈F(X*),X-X*〉表示定义在ℝN上的内积.
最优化问题与变分不等式问题的关系如下:
命题1 假设存在一点X*∈K,满足min F(X),则X*是变分不等式问题X*∈X∶〈F(X*),X-X*〉≥0;∀X∈K的解.其中F(X*)表示F对X 各个分量的梯度,且
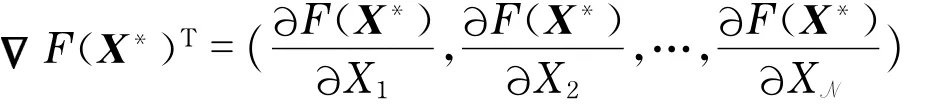
命题2 假设F(X)是凸函数,且X*满足X*∈X∶〈F(X*),X-X*〉≥0;∀X∈K,则有F(X*)=F(X).
定理1 假设F(X)是定义在K上的连续可微函数,其雅可比矩阵

是对称且半正定的,即F是凸函数,则存在一个实值函数
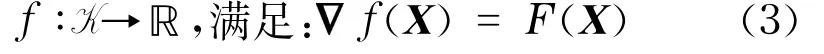
且变分不等式VI(F,K)的解X*亦是最优化问题min F(X)的解.如此说明最优化问题可以转化为变分不等式问题来求解,而变分不等式问题可以用投影算法快速准确地求解.
3.1.2 投影算法
解变分不等式的投影算法[17,44]步骤如下:
步骤1 初始化
令X0∈K且T=0.其中,K为有限集,T为迭代计数器(或时间段).
步骤2 计算

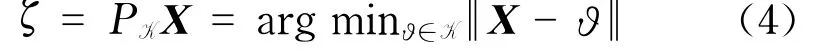
步骤3 收敛验证
3.1.3 基于变分不等式的研究现状
利用变分不等式研究超网络即将网络最优化问题转换为变分不等式问题进行求解.首先定义变量,将超网络平衡模型转化为最优化问题;然后将最优化问题转化为进化变分不等式问题,并对变分不等式问题解的存在性和唯一性进行论证;最后利用投影算法或修改后的投影算法求解变分不等式问题,得到变分不等式的解并通过实例计算和分析,研究超网络模型的特征.基于变分不等式的研究主要是寻找网络优化的平衡点,是从超网络整体层面进行的研究.
基于变分不等式的超网络研究,为超网络平衡问题研究,研究者有Nagurney、董琼、王志平等. Nagurney等为解决信息网、资金网与物流网的交互问题,构建以利润最大化为决策目标,决策者实行层内竞争、层间合作准则,并由生产商、销售商、需求市场组成的3层供应链超网络模型[18].同时求解该模型在固定条件下的变分不等式问题,得到模型达到均衡时的交易量和交易价格.随后该方法被广泛借鉴,分别用于解决考虑加入电子商务[45-46]、决策目标变化影响[21]、融合关系价值和社会责任[47]的物流供应链超网络模型;考虑需求、运输时间、价格、环境不确定性和风险管理影响的物流供应链超网络动态模型[48-51]和电力供应链超网络模型[52-54];考虑国家、货币、社会网络与金融工程影响的全球供应链超网络动态模型[55-57];考虑决策目标变化影响的知识密集型系统超网络模型[58];以及退货超网络模型[59]、回收超网络模型[60]、闭环供应链超网络模型[61]、交通运输超网络模型[35,62]、港口运输超网络模型[63]、网络广告资源分配和网络广告的超网络模型[64-65]等的平衡问题.该方法也用于考虑生产中断风险的供应链网络设计[66];活动—出行行为研究[67]以及运输网络、金融网络、拥塞网络和基础设施网络的鲁棒性研究[68-69].
3.2 基于超图的研究方法
3.2.1 基本概念
定义4 超图的阶与秩
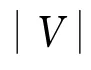
定义5 超链与超路
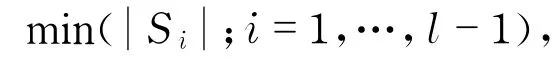
定义6 邻接矩阵[32]
H的邻接矩阵A(H):各行各列均与超网络节点相关,元素aij为与节点vi,vj均关联的超边数,aii=0.A(H)是对称矩阵,存在单位正交矩阵U=(uij),使得A=UDUT,其中D=Diag(λ1,λ2,…,λN)(N为阶)是A的特征值.
定义7 子超图
有J={1,…,m},且B⊂V,若H(B,J)={Ej∩B:j∈J,Ej∩B≠Ø},称H(B,J)为超图H的由B与J组成的子超图[23].
3.2.2 基于超图的研究思想
基于超图的研究方法多用于解决网络研究中边与节点不同质的问题,用超图描述系统,并研究网络的统计特性.首先分析系统,得到超图的节点集与超边集;然后对超图的超边与节点赋权,并得到超图中的超链、超路、关联矩阵等数据;最后定义需要的参数,并用得到的数据表述参数,得到相关的系统特征或网络性质.基于超图的超网络研究方法侧重于在保证边和节点同质性的前提下,描述超图网络的统计特性等特征.
基于超图的超网络研究,虽仍处于模型的构建和描述阶段,却受到各领域研究者的广泛关注,研究者有王众托、Ernesto、Jose等.他们分别将超图与图像处理相结合[72-73],提出新的聚类算法[74],用超图来辨别DNA切片[75-76]和研究模式分类[77],并构建相应的超网络模型;分别构建信息存储和获取[78]与描述乐器演奏相似细节[79]的超网络模型;分别构建基于图像和文本的超网络模型[80]、多通道信息检索中的跨通道图像与文本关键字生成的分层超网络模型[81]以及有向超网络模型[82];并对超网络的聚类系数和子图向心性等统计特性进行研究[12,23].
3.3 基于系统科学的研究方法
超网络是系统的抽象描述,所以系统科学的研究方法亦适用于超网络研究.系统科学着重考察系统的关系和属性,揭示系统活动规律,探讨系统理论和方法,在研究的过程中注重掌握系统的结构性和整体性等基本特征.故基于系统科学的研究思想如下:首先研究分析系统、子系统、要素等元素,并构建相应的超网络、网络模型;随后研究网络间关系、要素间关系、网络与要素间关系等局部性特征;最后研究超网络的整体性、等级结构性等全局特性,得到整个超网络的特征以及其它自定义特征.
基于系统科学的超网络研究,研究者有党延忠、席运江等,他们在分析知识点内在联系和知识存储类型的基础上,先后构建专家领域知识点模型[14],由知识点、知识主体两类节点与相关关联组成的加权知识超网络模型[83],加入物质载体及相关关联的无权组织知识超网络模型[4];定义和分析组织的专有知识与专有知识加权比率、核心领域知识网络抗毁性、组织成员知识重要度等参数;确定组织的易流失知识和易流失领域,分析知识主体的知识构成,确定有效的人才培养方案[15];分析节点的平均链接和初始转移节点数,从联系强度和知识显著持有者两个角度,分析现实网络形态下知识转移的动力行为[84];提出表示组织知识存量、个人知识存量[85]与组织知识搜索定位的方法[86],并定义组织知识广度和组织知识深度,分析组织知识的传播趋势[87].目前又构建了一个含管理层和物理层的快递超网络模型[13],通过定义配送网点间的连接矩阵Eα、基于成本的最短路矩阵W、路由矩阵Rc,通过改进的Floyd算法,探讨基于成本的快递超网络优化方法.
4 超网络应用
超网络发展虽只有短短十数年时间,但其本身就是为辅助其它领域研究而产生和发展起来的新兴领域,现有诸多应用成果,本节将列举一些典型应用并举例介绍.
4.1 超网络在退货供应链网络平衡问题中的应用
考虑一个含M个制造商,N个分销商,O个需求市场且决策目标为利润最大化的供应链网络,其中制造商生产的是同一种或者具有相同价值的产品,同时只考虑允许分销商退货的情形[21,59],模型如图5所示.
4.1.1 定义参数
分销商n与制造商m间的产品订购量与退货量分别为qmnmn;分销商n与需求市场o间的交易量为qno;Q1,Q2,Q3分别表示以qmnmn,qno为元素的向量;制造商m的批发价为ρ1m;分销商n的分销价为γn,实际售价为ρ2n;需求市场o的需求价为ρ3o;制造商m的生产费用为fm;单位回收价格为wm;分别从制造商m与分销商n角度考虑,制造商m与分销商n交易时的交易费用为cmn,mn;以及从需求市场o角度考虑,需求市场o与分销商n的交易费用为no;分销商n的展示存储费用为cn;需求市场o对产品的需求量为do.

图5 退货逆向供应链超网络模型[59]Fig.5 Return supply chain supermetwork model[59]
4.1.2 优化条件
a.制造商的优化目标
考虑层内竞争,制造商m的生产费用fm与订购量qm和退货量m有关:∀m,fm=fm(Q1,m);制造商m与分销商n间的交易费用cmn(运输费等)与交易量qmn有关:∀m,n,cmn= cmn(qmn).假定每退回单位产品,制造商m的损失费用为αm(假设其已知).则制造商m的决策目标可表示为

其中,对∀m=1,2,…,M;n=1,2,…,N,满足
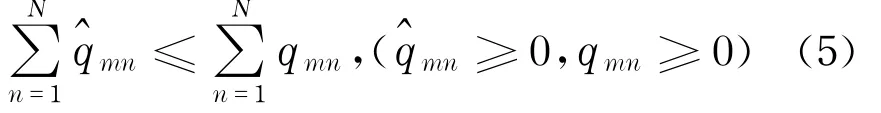
b.分销商的优化目标
考虑层内竞争,分销商n的产品处理费用cn(库存、产品展示费用等)与Q1有关:∀n,cn= cn(Q1);分销商n与制造商m间的交易费用mn也与交易量qmn有关.∀m,nmn=mn(qmn).假定每单位退货产品,分销商n的经济损失为βn(假定其固定),则分销商n的决策目标可表示为
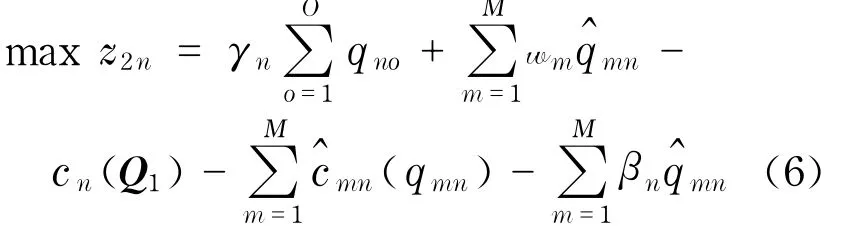
其中,对∀n=1,2,…,N,满足
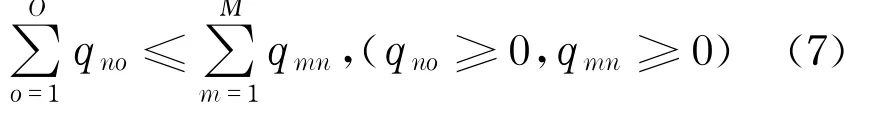
c.需求市场的优化目标
消费者在需求市场中购买单位产品支付的总费用ρ3o与商品价格γn和交易费用cno有关,故需求市场o对所有分销商n(n=1,2,…,N)满足

考虑层内竞争,需求市场o对产品的需求量与其它需求市场愿为产品支付的费用ρ3有关:∀o,do=do(ρ3).得到需求市场o(o=1,2,…,O)的供需平衡条件为

4.1.3 变分不等式问题
假设上一节得到方程fm,cmn,cn,mn均为连续可微的非负凹函数,do为连续递减函数,则有变分不等式

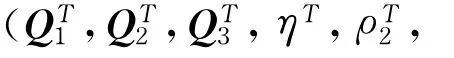

产品退货量为

产品交易量为
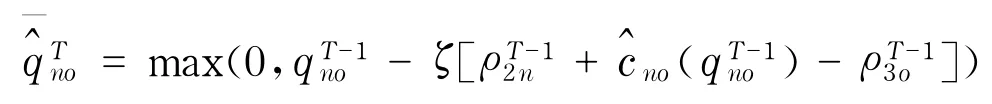
需求市场为单位产品支付的总费用为
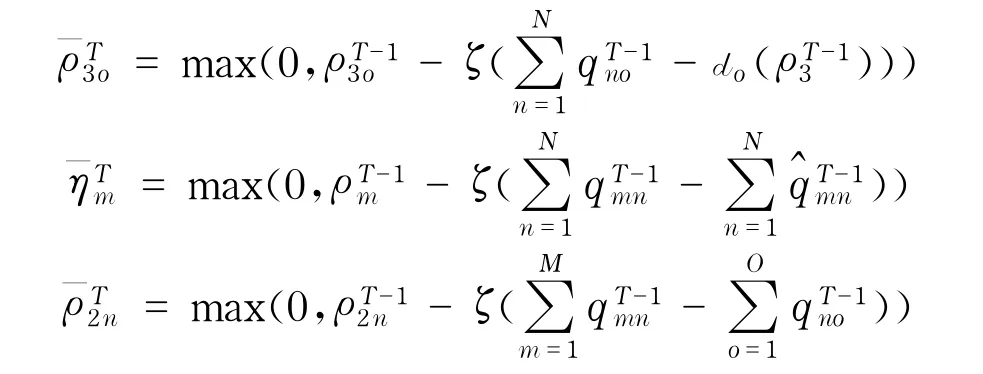
其中,T为迭代次数,ζ为迭代步长,详细计算过程参考文献[59].

4.2 超网络在知识表述中的应用
主题的辨别和提取是知识模型构建的重要环节,能够表述“这个主题是关于什么的”的词语是主题描述符;能够表述“什么是能够得到类似信息的好询问语句”的是主题鉴别符[21].
为生成和辨别正确的主题,Maguitman[88]建议用超图来表述词语、文档和主体间的关系.王众托院士对此作出研究[34],以词语为节点t,以文档为超边d,构造以文档为中心的超图H=(T,D),其对偶超图为以词语为中心的超图H*=(D,T),有实例如图6所示(见下页).
图6(a)是以文档为中心的超图H=({1,2,3,4},{A,B,C}),其中,{A,B,C}为文档集,{1,2,3,4}为词语集.图6(b)为它的对偶超图H*,图中,圈代表边,三角代表节点,数字代表节点在超边中出现的次数.

图6 用超图表示文档[34]Fig.6 Representation of documents by supernetworks diagram[34]
以文档为中心的超图的关联矩阵H:行与h个文档关联,列与h个词语关联,对应的元素H[i,j]=κ,κ为第j列词语在第i行文档中出现的次数,对偶图的关联矩阵为该矩阵的转置.
定义两个函数分别衡量词语j在文档i中的描述能力与鉴别能力:
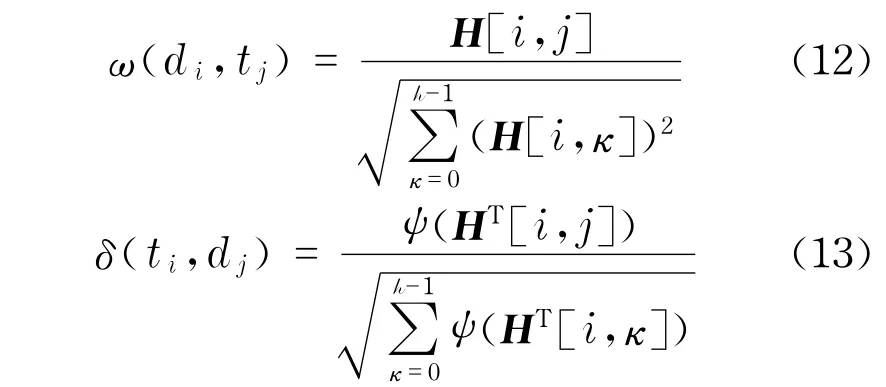
式(12)与(13)可分别用于构建以文档为中心的加权超图(图6(c),d-超图)和以词语为中心的加权超图(图6(d),t-超图),图中权重越大,则代表该词语对文档的描述能力或鉴别能力越强.在式(13)中,当κ>0时,ψ(κ)=1;当κ=0时,ψ(κ)= 0.d-超图与t-超图满足:∑j(ω(di,tj))2=1与∑j(δ(ti,dj))2=1.
以上方法仅针对文档,主题总涉及多个类似文档或词语,故需要研究文档的相似性与词语的同时出现性.

式(14)衡量文档di与dj间的相似性,式(15)衡量词语ti与tj的同时出现性.哪种词语是好的主题鉴别符,哪种词语又是好的主题描述符呢?定义如下函数


式(16)度量词语的主题鉴别能力,即ti对dj的鉴别力,取决于dj与ti鉴别出文档的相似性.式(17)度量词语的主题描述能力,即tj对di的描述力,取决于tj是否存在于其它与di相似的文档中;若无文档与di相似,描述力为0.找到好的主题,即可构建知识超网络模型.
4.3 超网络在知识网络鲁棒性研究中的应用
若移走少量节点后网络中的绝大部分节点仍连通,则称该网络的连通性对节点故障具有鲁棒性.对知识网络鲁棒性的研究,可用于组织知识资源的安全性评估、发现易流失知识以及评价组织成员的知识重要性等[83].本节将通过关联节点删除的方法来研究知识网络的鲁棒性.
4.3.1 加权知识超网络模型
组织知识体系包含若干知识领域,每一领域又包含若干子领域,对子领域再度划分,直到得到无法再分的知识单元为止[14].不论知识领域,还是知识单元,都是知识体系的组成部分,故可认为组织知识体系由许多大小不同的知识点组成.
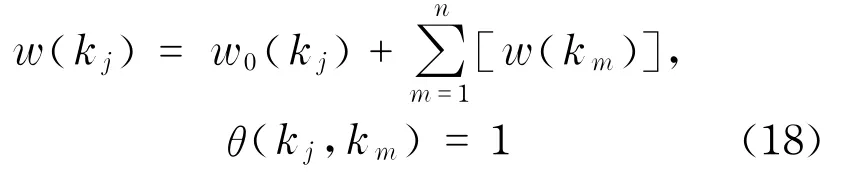
其中,w0(kj)为kj的初始权重;θ(kj,km)=1表示kj为km的父节点.式(18)说明父节点的权重值等于其初始权重与所有子节点权重之和.由此可得到加权知识超网络WKS=(K,W(K),P,Ek-k,Ep-p,Ep-k).
4.3.2 鲁棒性分析与度量
鲁棒性分析方法:在移除知识主体节点pi的同时,移除关系集Ep-k中所有与该节点相关的知识点kj与权重wij,然后考察其对知识点网络的影响,可表示为

鲁棒性度量方法:

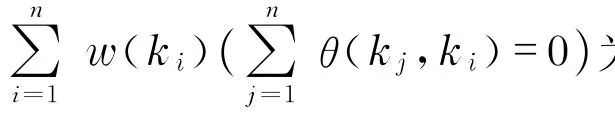
c.知识网络抗毁性表示造成一定比例知识流失需移除的最少人数.将组织中尤为重要的知识称为核心领域知识,则核心领域知识网络抗毁性表示造成一定比例核心领域知识流失需移除的最少人数(或人数比率).令布尔变量U(ki)表示ki是否为核心领域知识.
4.3.3 鲁棒性应用分析
a.组织知识资源安全性评价:组织知识资源安全性与专有知识率成反比;与核心知识网络抗毁性成正比.
b.组织成员知识重要性评价:个人知识比重指知识总量中个人知识所占加权比重,可表示为
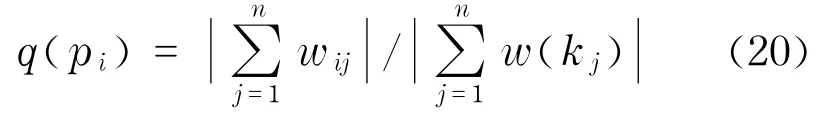
个人核心领域知识比重指组织核心领域知识中个人知识所占比重,可表示为
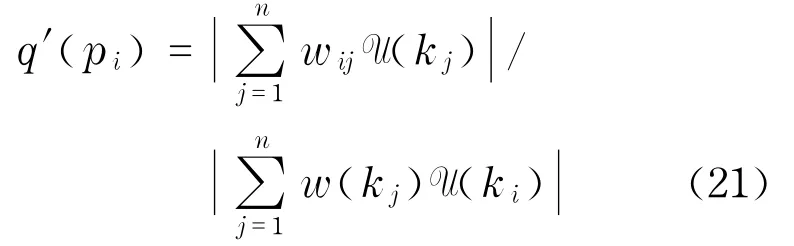
同时,可以根据专有知识集、个人知识比重等确定组织中的易流失知识,制定完善的知识培训计划.
4.4 超网络的统计学特性研究
复杂网络的“无标度性”、“小世界特性”等统计特性,开辟了复杂网络研究的新纪元.Estrada等用超图理论对聚类系数、子图向心性等参数进行延伸,并分别用二部图和超图研究合作网络、生态网络及1990年美国合作经济网络的平均度、子图向心性和聚类系数[12,23].最终认为超图理论能更好地刻画网络的细节,更好地描述真实网络的信息.
4.4.1 子图向心性
假设有超图H=(E,V),其中E={E1,E2,…,ET}为超边集,V={v1,v2,…,vL}为节点集,A为超图的L阶邻接矩阵,且有单位正交矩阵U=(uij),使得A=UDUT,其中D=Diag(λ1,λ2,…,λL)(L为阶)是A的特征值,若vi,vj为H的节点,Ak中位置(i,j)的元素为vi→vj的步长为k的路径数
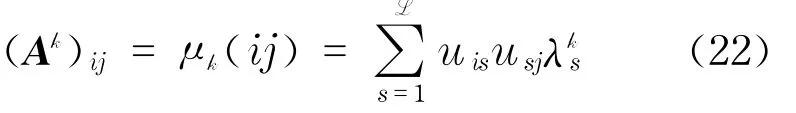
若i=j,有
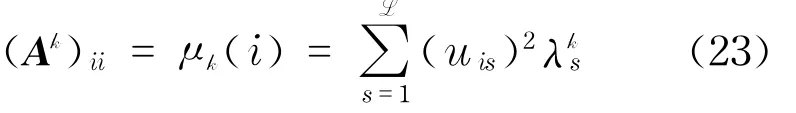
H中步长为k的链总数Wk与闭链总数C Wk分别为

超网络中以vi为起终点的各种步长的闭链总数被称为节点vi的子图向心性[23]CSH(i).

如此,超图的平均子图向心性为

4.4.2 聚类系数
Watts[2]等提出聚类系数来描述复杂网络中节点间的相互关联程度,Estrada对其进行延伸,得到超网络的聚类系数[23]为


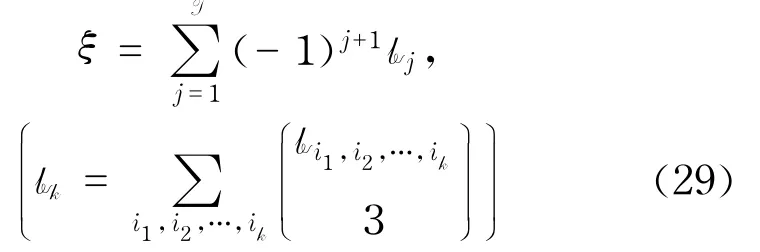
同时,伪步长为2的超路数p=3ξ,得到最终公式为
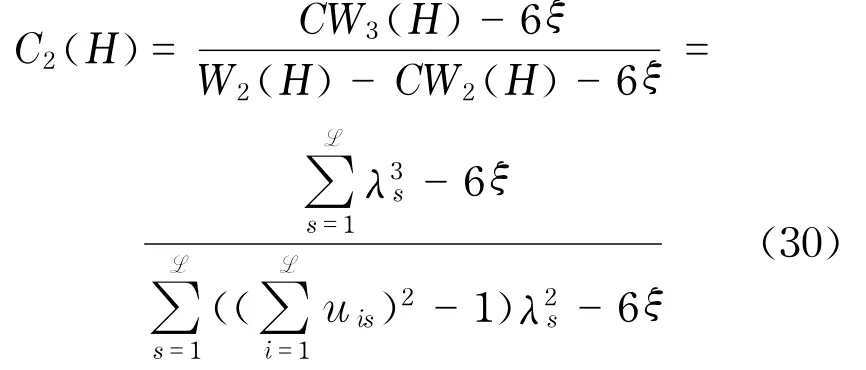
5 总结和展望
本文主要介绍与探讨了超网络的基本概念、常见模型、研究方法和发展状况,罗列了现阶段取得的研究成果,举例说明了超网络在各研究领域的应用及其统计特性.在对超网络的现有研究成果学习和理解时,需客观认识到超网络研究的提出和发展时间尚短,目前仍处于初级探讨阶段,存在诸多不足:a.研究方法单一.目前超网络的常见研究方法有3种:基于变分不等式、基于超图理论和基于系统科学的研究方法.其中基于变分不等式的研究方法更是拥有近乎固定的算法步骤,亟待出现新的研究方法丰富和拓展今后的研究思路.b.研究深度不足.基于变分不等式的研究方法虽已成熟,并用于构造和分析多种超网络模型的平衡问题.然而,超网络提出的初衷是为更精确地研究和描述现实综合网络,目前并未体现超网络中网络间关系等方面的研究.另外,基于超图理论的研究方法和基于系统科学的研究方法均处于探索阶段.虽然,超网络研究发展已有十数年,但超网络的特征和统计特性等方面的研究成果寥寥.c.研究广度不足.超网络研究源于本世纪初,从事该领域研究的人员数、发表的高质量论文数、涉及到的领域、学科虽在不断增长,但与其它研究领域相比仍略显有限,急需拓宽超网络模型的应用领域和范围.
综上所述,超网络研究今后可考虑以下问题:a.超网络的概念、统计特性,回答“什么是超网络,可将具有何种特征的网络看作超网络,它的边界是什么,有哪些统计特性等”.b.综合网络研究,如何提高变分不等式算法,使不只是研究单一网络平衡问题,而是研究综合网络平衡问题.例如不只是将运输网络转换为供应链网络的流或权,而是将两种网络进行综合研究.c.超网络与复杂网络的关系.如何区分复杂网络和超网络,二者之间有什么联系和区别.超网络与复杂巨系统有什么联系?超网络被认为“高于而又超于”现存网络,那它与系统工程界的“系统的系统”又有什么关系?系统是动态的系统,网络自然也是动态的网络,超网络中时刻都有点、边、流的生成与消失,即超网络与时间概念密切相关,在研究中应当如何体现.
[1] Faloutsos M,Faloutsos P,Faloutsos C.On power-law relationships of the internet topology[J].Computer Communication Review,1999,29(4):251-262.
[2] Watts D J,Strogatz S H.Collective dynamics of‘small-world’networks[J].Nature,1998,393(6684):440-442.
[3] Hethcote H W.The mathematics of infectious diseases[J].SIAM Review,2000,42(4):599-653.
[4] 席运江,党延忠,廖开际.组织知识系统的知识超网络模型及应用[J].管理科学学报,2009,12(3):12-21.
[5] 周涛,柏文洁,汪秉宏,等.复杂网络研究概述[J].物理,2005,34(1):31-36.
[6] Erdos P,Renyi A.On the evolution of random graphs[M].Budapest:Publications of the Mathematical Institute of the Hungarian Academy of Sciences,1960.
[7] Newman M E J,Watts D J.Renormalization group analysis of the small-world network model[J].Physical Letters A,1999,263(4):341-346.
[8] Zhou S,Mondragon R J.Towards modeling the internet topology——the interactive growth model[C]∥Proceedings of the 18th International Teletraffic Congress.Berlin,2003.
[9] Barabasi A L,Albert R.Emergence of scaling in random networks[J].Science,1999,286(5439):509 -512.
[10] Williams R J,Martinez N D.Simple rules yield complex food webs[J].Nature,2000,404(6774):180 -183.
[11] Lancioni R,Schau H J,Smith M F.Internet impacts on supply chain management[J].Industrial Marketing Management,2003,32(3):173-175.
[12] Estrada E,Rodrigues V R.Subgraphcentrality in complex networks[J].Physical Review E,2005,71(5):1-9.
[13] 黄建华,党延忠.快递超网络模型及基于成本的优化方法[J].系统管理学报,2010,19(6):689-695.
[14] 席运江,党延忠.基于知识网络的专家领域知识发现及表示方法[J].系统工程,2005,23(8):110-115.
[15] 于洋,党延忠.组织人才培养的超网络模型[J].系统工程理论与实践,2009,29(4):154-160.
[16] Sheffi Y.Urban transportation networks:equilibrium analysis with mathematical programming methods[M].NJ:PrenticeHall,1985.
[17] Nagurney A,Dong J.Supernetworks:decision-making for the information age[M].Cheltenham:Edward Elgar Publishers,2002.
[18] Nagurney A,Dong J,Zhang D.A supply chain network equilibrium model[J].Transportation Research E,2002,38(5):281-303.
[19] Nagurney A,Wakolbinger T.Supernetworks:an introduction to the concept and its applications with a specific focus on knowledge supernetworks[J]. International Journal of Knowledge Culture and Change Management,2005,4(1):1-16.
[20] Nagurney A.Supernetworks:the science of complexity[J].上海理工大学学报,2011,33(3):205-228.
[21] 王志平,王众托.超网络理论及其应用[M].北京:科学出版社,2008.
[22] Matsypural D,Nagurney A,Liu Z.Modeling of electric power supply network with fuel suppliers via variational inequalities[J].International Journal of Emerging Electric Power Systems,2007,8(1):1-5.
[23] Estrada E,Rodrigues V R.Subgraph centrality and clustering in complex hyper-networks[J].Physical A,2006,364(1):581-594.
[24] Sonntag M,Teichert H M.Competition hypergraphs[J].Discrete Applied Mathematics,2004,143(1):324 -329.
[25] Emmerink R H M,Axhausen K W,Nijkamp P,et al. Effects of information in road transport network with recurrent congestion[J].Transportation,1995,22(1):21-53.
[26] Low S H,Paganini F,Doyle J C.Internet congestion control[J].Control Systems,2002,22(1):28-43.
[27] 雷延军,李向阳.军事供应链“超网络”结构模型研究[J].物流科技,2006,29(136):60-62.
[28] Berge C.Graphs and hypergraphs[M].New York:Elsevier,1973.
[29] Berge C.Hypergraphs:the theory of finite sets[M]. Amsterdam:Elsevier Science,1989.
[30] 黄汝激.超网络的有向k超树分析法[J].电子科学学刊,1987,19(3):244-255.
[31] Tuan N D.Hypergraphical t-designs[J].Discrete Mathematics,2006,306(12):1189-1197.
[32] Gazdik I.Modeling system by hypergraphs[J]. Kybernetes,2006,35(9):1369-1381.
[33] Frank H,Page J,Myrna H,et al.Networks and farsighted stability[J].Journal of Economics Theory,2005,120(2):257-269.
[34] 王众托.关于超网络的一点思考[J].上海理工大学学报,2011,33(3):229-237.
[35] Yamada T,Imai K,Nakamura T,et al.A supply chaintransport supernetwork equilibrium model with the behavior of freight carriers[J].Transportation Research Part E,2011,47(6):887-907.
[36] Temkin O N,Zeigarnik A V,Bonchev D.Chemical reaction networks:a graph-theoretical approach[M]. Florida:CRCPress,1996.
[37] Nagurney A,Dong J.A multiclass,multicriteria traffic network equilibrium model with elastic demand[J]. Transportation Research Part B,2002,36(5):445 -469.
[38] Dong J,Zhang D,Yan H,et al.Multitered supply chain nerworks:multicriteria decision-making under risk and uncertainty[J].Annals of Operations Research,2005,41(6):585-612.
[39] Bonacich P,Holdren A C,Johnston M.Hyper-edges and multidimensional centrality[J].Social Networks,2004,26(3):189-203.
[40] Pothen A,Ramadan E,Tarafdar A.Ahypergraph model for the yeast protein complex network[C]∥Proceedings of HICOMB,Santa Fe NM,2004.
[41] Krishnamurthy L,Nadeau J,Ozsoyoglu G,et al. Pathways database system:an integrated system for biological pathways[J].Bio-informatics,2003,19(8):930-937.
[42] Lions I J L,Stampacchia G.Variational inequalities[J].Communications on Pure and Applied Mathematics,1967,20(3):493-519.
[43] Daniele P,Maugeri A,Oettli W.Time-dependent traffic equilibria[J].Journal of Optimization Theory and Applications,1999,103(3):543-555.
[44] Cojocaru M G,Daniele P,Nagurney A.Projected dynamical system and evolutionary variational inequalities via hilbert spaces with applications[J]. Journal of Optimization Theory and Applications,2005,27(3):1-15.
[45] Nagurney A,Loo J,Dong J,et al.Supply chain networks and electronic commerce:a theoretical perspective[J].Netnomics,2002,4(2):187-220.
[46] Dong J,Zhang D,Nagurney A.Supply chain networks with multicriteria decision-maker[C]∥Proceedings of the 15th International Symposium on Transportation and Traffic Theory.Adelaide,2002.
[47] Cruz J.Dynamics of supply chain networks with corporate social responsibility through integrated environmental decision-making[J].European Journal of Operational Research,2008,184(3):1005-1031.
[48] Dong J,Zhang D,Nagurney A.A supply chain network equilibrium model with random demands[J].European Journal of Operational Research,2004,156(1):194 -212
[49] Nagurney A,Cruz J,Dong J,et al.Supply chain networks,electronic commerce,and supply side and demand side risk[J].European Journal of Operational Research,2005,164(1):120-142.
[50] Nagurney A,Matsypura D.Global supply chain network dynamics with multicriteria decision-making under risk and uncertainty[J].Transportation Research E,2005,41(6):585-612.
[51] 柯珂,樊智,佘震宇,等.超网络时代的电子金融和风险管理[J].上海理工大学学报,2011,33(3):258 -263.
[52] Nagurney A,Liu Z,Woolley T.Optimal endogenous carbon taxes for electric power supply chains with power plants[J].Mathe matical and Computer Modeling,2006,44(9):899-916.
[53] Nagurney A,Liu Z,Cojocaru M,et al.Dynamic electric power supply chain and transportation networks:an evolutionary variational inequality formulation[J]. Transportation Research E,2007,43(5):624-646.
[54] Liu Z,Nagurney A.An integrated electric power supply chain and fuel market network framework:theoretical modeling with empirical analysis for New England[J].Naval Research Logistics,2009,56(7):600-624.
[55] Nagurney A,Cruz J,Matsypura D.Dynamics of global supply chain supernetworks[J].Mathematical and Computer Modeling,2003,37(9):963-983.
[56] Nagurney A,Ke K.Financial networks with intermediation:risk management with variable weights[J].European Journal of Operational Research,2006,172(1):40-63.
[57] Cruz J,Nagurney A,Wakolbinger T.Financial engineering of the integration of global supply chain networks and social networks with risk management[J].Naval Research Logistics,2006,53(7):674-696.
[58] Nagurney A,Dong J.Management of knowledge intensive system as supernetworks:modeling,analysis,computations and applications[J]. Mathematical and Computer Modeling,2005,42(3):397-417.
[59] Wang Z P,Zhang F M,Wang Z T.Research return supply chain supernetwork model based on variational inequalities[C]∥Proceedings of IEEE international conference on automation and logistics.Jinan,2007.
[60] Nagurney A,Toyasaki F.Reverse supply chainmanagement and electronic waste recycling:a multitiered network equilibrium framework for ecycling[J].Transportation Research E,2005,41(1):1 -28.
[61] Hammond D,Beullens P.Closed-loop supply chain network equilibrium under legislation[J].European Journal of Operational Research,2007,183(2):895 -908.
[62] Nagurney A.On the relationship between supply chain and transportation network equilibria:a supernetwork equivalence with computations[J].Transportation Research Part E,2006,42(4):293-316.
[63] Xie H Y,Zhao D P,Yuan Z J,et al.Port supply chain supernetwork optimization based on variational inequalities[C]∥International Conference on Logistics System and Intelligent Management.Harbin,2010.
[64] 王志平,周生宝,郭俊芳,等.基于变分不等式的网络广告资源分配的超网络模型[J].大连海事大学学报,2007,33(4):26-30.
[65] Zhao L,Nagurney A.A network modeling equilibrium for internet advertising:models,qualitative analysis and algorithms[J].European Journal of Operational Research,2008,187(2):456-472.
[66] 刘祖刚.生产中断风险下的供应链网络设计[J].上海理工大学学报,2011,33(3):264-267.
[67] Ukkusuri G R.Dynamic user equilibrium model for combined activity-travel choices using activity-travel supernetwork representation[J].Networks&Spatial Economics,2010,10(2):273-292.
[68] Nagurney A,Qiang Q.Robustness of transportation networks subject to degradable links[J].Europhysics Letters,2007,80(6):1-6.
[69] Nagurney A,Qiang Q.A network efficiency measure for congested networks[J].Europhysics Letters,2007,79(3):1-5.
[70] 许小满,孙雨耕,杨山,等.超图理论及其应用[J].电子学报,1994,22(8):65-71.
[71] 王建方,李东.超图的路与圈[J].中国科学(A辑),1998,28(9):769-778.
[72] Bretto A,Gillibert L.Hypergraph-based image representation[C]//Lecture Notes in Computer Science.Heidelberg:Springer Berlin,2005.
[73] Bretto A,Cherifi H,Aboutajdine D.Hypergraph imaging:an overview[J].Pattern Recongition,2002,35(3):651-658.
[74] Ozdal M,Aykanat C.Hypergraph models and algorithms for date-pattern-based clustering[J].Data mining and Knowledge Discovery,2004,9(1):29 -57.
[75] Segovia-Juarez L,Colombano S,Kirschner D. Identifying DNAsplice sites using hypernetworks with artificial molecular evolution[J].Biosystems,2007,87(2/3):117-124.
[76] Wang K Y,Kim B S,Lee C H,et al.CVD level prediction processor using DNA computing[J]. Electronics Express,2009,6(9):529-534.
[77] Kim J K,Zhang B T.Evolving hypernetworks for pattern classification[C]∥IEEE Congress on Evolutionary Computation.Singapore,2007.
[78] Mao C,Yokomori T.DNA hypernetworks for information storage and retrieval[C]∥Lecture Notes in Computer Science.Heidelberg:Springer Berlin,2006.
[79] Maeshiro T,Maeshiro M,Shimohara K,et al. Hypernetwork model to represent similarity details applied to musical instrument performance[C]∥Lecture Notes in Computer Science.Heidelberg:Springer Berlin,2009.
[80] Heo M,Kang M,Zhang B.Visual query expansion via incremental hypernetwork models of image and text[C]∥PRICAI 2010:Trends in Artificial Intelligence. Heidelberg:Springer Berlin,2010.
[81] Ha J W,Kim B H,Lee B,et al.Layered hypernetwork models for cross-modal associative text and image keyword generation in multimodal information retrieval[C]∥PRICAI 2010:Trends in Artificial Intelligence.Heidelberg:Springer Berlin,2010.
[82] Volpentesta AP.Hypernetworks in a directed hypergraph[J].European Journal of Operational Research,2008,188(2):390-405.
[83] 席运江,党延忠.基于加权超网络模型的知识网络鲁棒性分析与应用[J].系统工程理论与实践,2007,27(4):134-140.
[84] 徐升华,邹宏.基于超网络模型的知识转移动力分析[J].情报杂志,2011,30(7):94-98.
[85] 席运江,党延忠.基于加权超网络模型的组织知识存量表示方法[J].情报学报,2007,26(2):210-215.
[86] 席运江,党延忠.一种基于加权超网络模型的组织知识搜索定位方法[J].情报学报,2008,27(1):24-29.
[87] 于洋,党延忠,吴江宁,等.基于超网络的知识传播趋势分析[J].情报学报,2010,29(2):356-361.
[88] Maguitman A G.Intelligent support for knowledge capture and construction[D].Indianapolis:Indiana University,2004.
(编辑:丁红艺)
Brief Review of Supernetwor ks
QIYu-hu1, GUOJin-li1,2
(1.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China;2.Center for Supernetworks Research,University of Shanghai for Science and Technology,Shanghai 200093,China)
As a new method for studying complex systems and problems,supernetworks begin to attract close attention after the research boom on complex network,meanwhile it is widely used to solve practical problems.The basic concepts,characters,and models of supernetworks were introduced.The research methodology based on variational inequality,hypergraph and systems science was summurized,and the research status was reviewed respectively.The applications of supernetworks to network equilibrium,knowledge network expression and robustness study were described,and the statistic characteristics were discussed.The inadequacy in the research on supernetwork at present was pointed out and the future work was discussed.
supernetwork;variational inequality;hypernetwork;statistical property
N 94
A
1007-6735(2013)03-0227-13
2012-11-12
国家自然科学基金资助项目(70871082);上海市一流学科建设资助项目(S1201YLXK)
漆玉虎(1987-),男,硕士研究生.研究方向:超网络、复杂网络、工业工程.E-mail:qiyunyi@126.com
郭进利(1960-),男,教授.研究方向:工业工程、复杂网络、人类行为动力学.E-mail:phd5816@163.com
