一类海洋生态动力系统最优捕获策略的数值模拟
2013-07-07李丹
李 丹
(浙江海洋学院 数理与信息学院,浙江 舟山 316004)
0 引言
生态动力学数值模拟研究是指用数学公式将光合作用过程和生物中的生态生理学过程和食物网中营养关系表示成源函数的形式,即将海水运动、海水中营养盐的输运和扩散、营养盐向浮游植物的转化以及生物捕食关系变成可以计算的形式.这是海洋生态动力学研究的一个重要方向.本文主要用理论推导和数值模拟相结合的方法,分析了模型的动力学特性并给出了以最大利润为目的的最优捕获策略的存在性.
1 问题的描述
考虑营养盐、自养浮游植物和食植鱼类相互作用关系,建立模型如下:

其中,N为营养盐浓度;P为浮游植物浓度;Z为食植鱼类浓度;e为污染强度;Rm为食植鱼类的最大摄食率;h为人类对食植鱼类的捕捞率。h为模型的参数,其它参数取值如下表1所示:

表1 参数意义及其取值
2 正平衡点的存在性
问题(1)的平衡点满足下列方程:
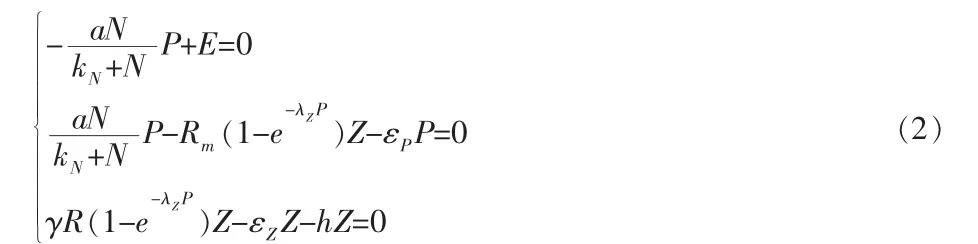
方程组(2)的解为:
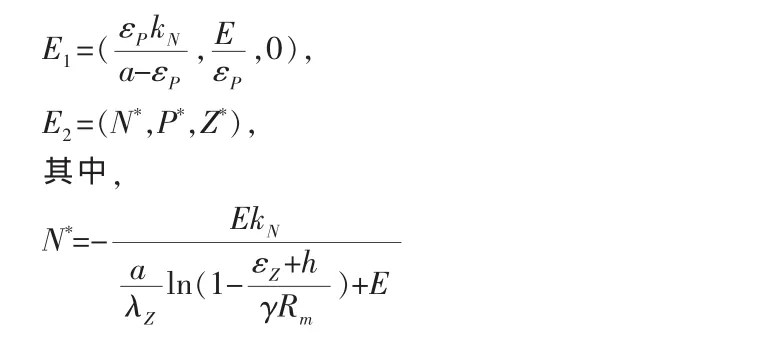

图1 函数d1d2-d3的图像

图2 函数Z*的图像

图3 函数 f(h)的图像

图4 函数 f′(h)的图像
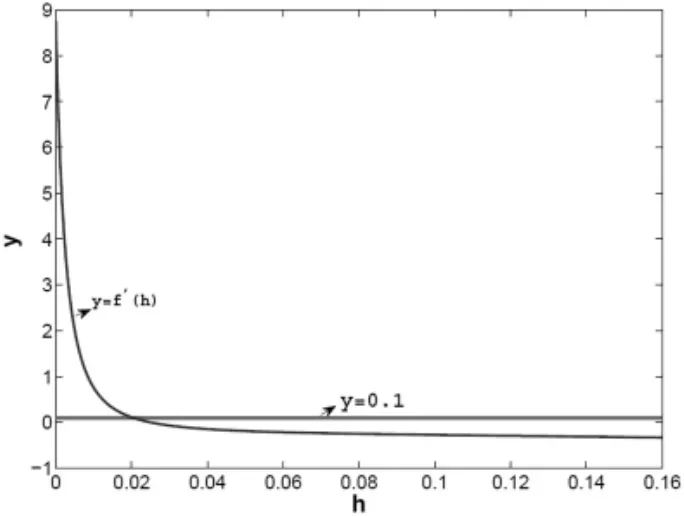
图5 函数y=f′(h)和y=0.1的图像

根据文[1],我们有如下结论.
定理 1 E1是系统(1)的非负平衡点.当 E=0.05,0<h<0.1544 时,E2是系统(1)的正平衡点.

文[1]中推导出了E2是系统(1)的稳定平衡点的条件包括d1d2-d3>0因为d1d2-d3包含超越函数,无法根据d1d2-d3>0给出h具体的表达式,我们通过Matlab软件画出了该超越函数在区间[0,0.16]的图像,并通过数值计算的搜索法得0.0002<h≤0.1544.
定理 2 当 E=0.05,h>0.1722 时,E1是系统(1)的稳定平衡点.当0.0002≤h<0.1544 时,E2是系统(1)的稳定平衡点.
4 以最大利润为目标的捕获策略
假设食植鱼在市场上单位价格为p1,单位捕获量的费用为常数c,利润Q≥0,则此时食植鱼的捕获产出量为Y(h)=hZ,利润为:
Q(h)=p1hZ*-ch.(3)
因为在平衡点E1中Z=0,下面我们只讨论E2平衡状态下的最优捕获策略.
将平衡点E2代人利润函数(3),可得:

上面的表达式非常复杂,不能求出函数Q(h)极值点的具体值,下面我们主要用Matlab软件画出函数图像,讨论最优捕获策略的存在性,且当p1,c已知时,可借助数值方法计算最优捕获量的近似值.
令 f(h)=h*Z*,由图 2-图 4 和数值计算可得如下结论:1)当 0<h<0.16,随着捕获率h的增加,食植鱼类的浓度逐渐减少并趋于0;2)当c/p1<8.7608 时,Q(h)在区间[0,0.16]内有且仅有一个极大值点;3)当c/p1=0.1 时,Q(h)在区间[0,0.16]内有且仅有一个极大值点,该点的近似值为 h=0.02045.
[1]王洪礼,董占琢.海洋生态系统非线性动力学研究[J].海洋技术,2009,28(1):50-54.
[2]孙嘉轶.几类捕食-食饵系统的最优捕获策略[D].哈尔滨:哈尔滨理工大学,2010.
[3]王高雄,周之铭,朱思铭,王寿松,编.常微分方程[M].3版.北京:高等教育出版社,2008.
[4]陈长胜.海洋生态系统动力学与模型[M].北京:高等教育出版社,2003.
