LINGO软件在木材运输优化模型中的应用
2013-07-06曾翔亮董希斌
曾翔亮,董希斌,崔 莉
(东北林业大学 工程技术学院,哈尔滨 150040)
1 概 述
在实际的木材运输中,除了少部分木材经过集材后直接从伐区楞场运输到需材点外,大部分木材基本上都要经过从林区采伐点到伐区楞场的集材段运输、伐区楞场到木材中转站再到需材点的多阶段运输[1]。由于木材运输是伐区生产的重要组成部分,因此木材运输方案的优劣对作业成本有着重要的影响,国内已经有不少学者建立了木材运输优化模型,并利用线性规划方法、遗传算法等优化算法对所建的模型进行求解[2]。但对于大规模的木材运输,尤其是当所建的模型比较复杂时,其计算量非常大,通过人工去进行计算求解,是无法想象的。并且在实际运输过程中,供材量和需材量等数据经常会随季节出现变动,给求解模型带来很大的不便。LINGO软件是美国LINDO公司推出的一款专门用于求解优化模型的软件,在数学、科研和工业界得到广泛应用[3]。它提供了一套完整的建模环境,以及一整套快速的求解器,方便灵活,在求解线性、非线性和整数优化模型上,具有人工计算甚至其它软件无法比拟的优势。
2 数学优化模型的建立
在实际的木材交易过程中,供材点一般都有一个最低订货量,只有当需材点的订货量不低于这个最低订货量时,供材点与需材点之间才会采用直达运输,否则供材点与需材点就会采用中转运输,即先由供材点把木材运往木材中转站,再由木材中转站统一对需材点进行配货。另外,有时虽然需材点的订货量超过供材点的最低订货量,但是如果通过中转运输的运输成本低于直达运输的运输成本,需材点一般也会选择中转运输。木材的直达、中转混合运输过程见图1。

图1 木材直达、中转混合运输图Fig.1 Direct-transit mixed transportation of timber
每个木材中转站都有一个吞吐能力,它是衡量木材中转站作业能力的重要参数。木材中转站作为供材点与需材点之间的中间环节,当木材由供材点运往木材中转站时,其相当于一个需材点,存在一个最大需求量;而当木材由木材中转站运往需材点时,其又相当于一个供材点,存在一个最大供应量。因此,木材中转站的最大需求量和最大供应量均为其吞吐能力的1/2。
在实际的木材运输中,对于某种木材来说,往往其供材点的总供应量与其需材点的总需求量是不相等的,有时会供过于求,有时会供不应求。当木材采用中转运输时,木材中转站相当于一个中间点,由于中间点只起转运作用,所以中间点的流量为零[4],即运出这点的木材总量与运进这点的木材总量之差为零。因此,当供材点某种木材的总供应量小于需材点的总需求量时,供材点虽会将该木材全部出售,但需材点对该木材的需求仍会出现不足;而供材点某种木材的总供应量大于需材点的总需求量时,供材点只会出售需材点对该木材所需要的量,此时供材点的该木材则会出现剩余。
综合考虑多种因素,木材运输成本最低的优化模型为:


每个表达式和各变量所表达的含义分别见表1和表2。

表1 表达式的含义Table1 Implication of each equation

表2 自变量的含义Table2 Implication of each symbol in equations
3 实例并用LINGO求解
某2个林场主要生产松树和杨树,这些木材主要以原木(含有多种等级)和原条的形式进行运输,选取这2个林场主要的5个楞场 [A1、A2、A3、A4、A5]为供材点,供材点下游有2个木材中转站P1、P2,木材中转站为其下游的4个需材点 [B1、B2、B3、B4]供应木材。木材中转站P1、P2的吞吐能力分别为400m3/月和500m3/月,每个需材点原木和原条的直达运输发货量起点限制量Ei分别为80m3和100m3。各木材的单位运输(汽车运输)费用及供求数量见表3[5]。

表3 木材的供求量及单位运输费用Table3 Supply and demand of timber and the unit transportation cost
由表3可见,供材点原木和原条的总供材量分别为:

因此,供材点原木的总供应量小于需材点原木的总需求量,而供材点原条的总供应量大于需材点原条的总需求量。根据建立的数学优化模型,在LINGO软件的模型窗口中输入如下代码:


单击LINGO/Solve菜单命令,即可得到最优的目标函数值,即最低的运输费用为131461元,同时得到优化模型的最优解,将得到的最优解整理后,见表4。
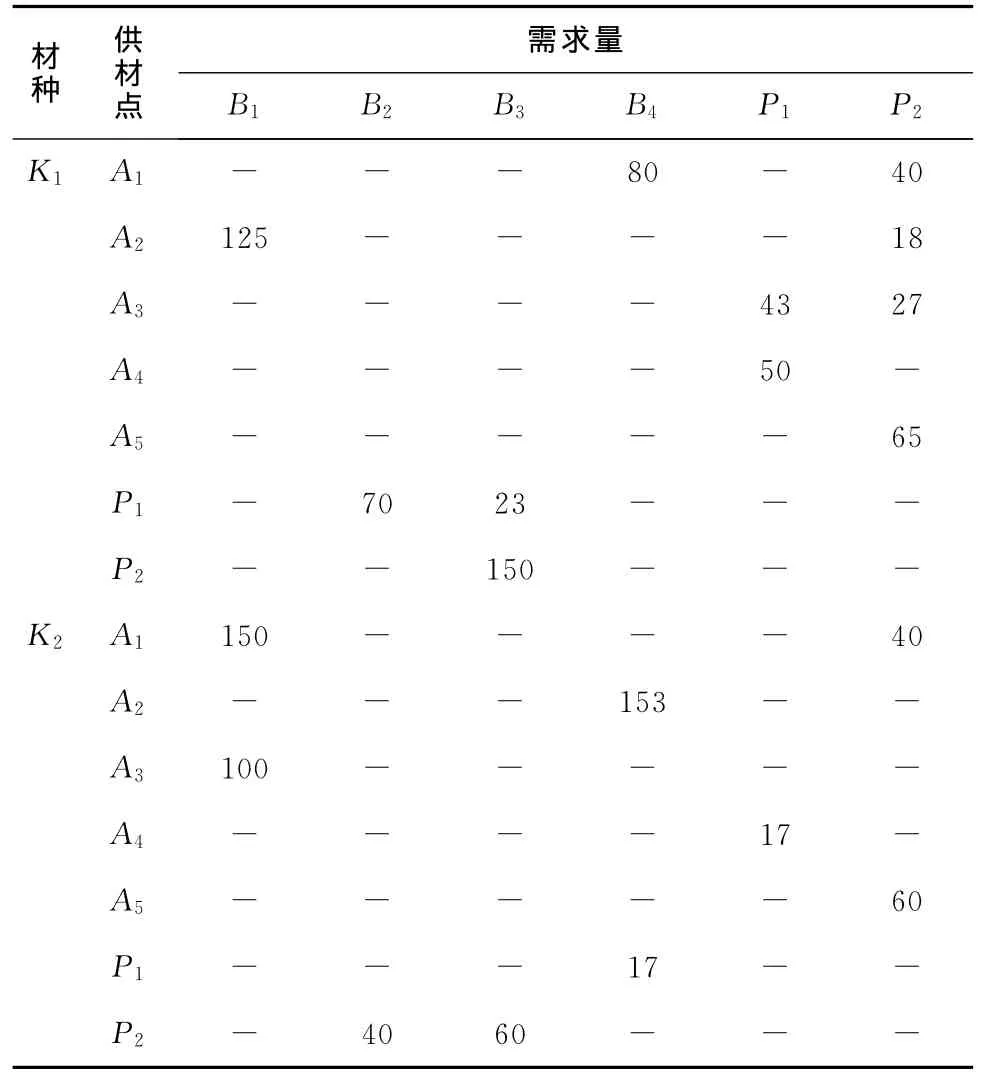
表4 最优运输方案Table4 Optimal transportation plan /m3
4 结 论
LINGO软件的模型语言与数学模型非常相似,不但直观易懂,而且LINGO软件中的模型一旦编好,就具有通用性,即使数学模型中数据发生变化,在LINGO中只要对模型窗口中的数据做出相应的修改,即可快速得到新的最优解,非常方便灵活。对于大规模的木材运输优化模型,使用LINGO软件可以轻而易举的对模型进行求解,在实际运输中值得推广。
本文只对木材的直达运输和中转运输建立了优化模型,并没有考虑在运输过程中发生的搬运、装卸、储存等费用,也未考虑森铁、水运等其它运输方式,因此,所建的木材运输优化模型还有待进一步完善。
[1]刘翠娜,邱荣祖.基于遗传算法的木材运输方案优化技术 [J].福建林学院学报,2010,30(4):380-384.
[2]李希胜,赵 尘.基于线性规划的采运作业优化决策方法 [J].西北林学院学报,2011,26(4):214-217.
[3]王 林,叶小侠.基于Lingo语言求解物流配送中心选址模型 [J].物流技术,2008,(10):113-115.
[4]白世贞.物流运筹学 [M].北京:中国物资出版社,2006.
[5]刘翠娜.木材物流系统优化研究 [D].福州:福建农林大学,2006.
