氯代苯结构与生物活(毒)性的GM(1,1)模型研究
2013-07-06余训爽
余训爽
(长江大学 化学与环境工程学院,湖北 荆州 434023)
0 引 言
随着人类社会对有机化合物需求的增大,它们给环境造成的危害或压力随之增加。每年新增的有机化合物种类繁多,有机化合物进入环境之前不可能逐一进行理化性质/生物活(毒)性的测定,如能从现有的实验数据探讨科学的、精确的、可靠的方法预测新化合物的生物活(毒)性(QSAR),从而进行环境风险评价,这样不仅方便、经济,也可避免实际测定时带来的二次污染。研究表明:QSAR在预测化合物生物活(毒)性方面扮演重要角色,成为环境、生命、毒理学等学科研究中的一个前沿领域[1-5]。在研究中,正辛醇/水分配系数(lgKOW)是最常见、最重要的理化参数。它反映有机物的亲脂性。根据实验测得的经验参数(辛醇-水分配系数、水中溶解度等)与相应的性质(如生物毒性、光解活性等)建立定量关系式。逐一测定各个有机化合物的理化参数,现实是不可能的;另外实验数据存在一定的误差,用失真的数据直接建模,预测时可能会导致预测结果失败。改变传统处理系统信息方法,还以数据本来面目,从而提高模型的预测能力,是从事QSAR工作者必须考虑的问题。
灰色系统理论以 “部分信息已知、部分信息未知”的 “小样本”、“贫信息”为研究对象,通过对“部分”已知的系统信息进行处理、分析、量化和建模[6]。从而实现处理数据不多的灰信息来揭示系统信息的特征和变化规律。本文将运用灰色理论对12种氯代苯的生物活(毒)性与其结构参数的定量构效关系进行研究。
1 GM(1,1)建模原理
1.1 GM(1,1)建模过程
GM(1,1)模型是1阶的、单变量的模型。本文依据连续非等时空距 GM(1,1)灰色模型[5,7]建立灰色预测模型。其具体步骤如下:
设系统某行为特征的自变量x(k)和观测值y(k)为:
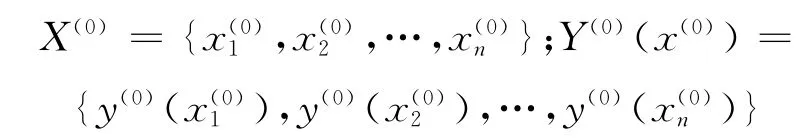
相应的1-AGO生成序列[6]为:
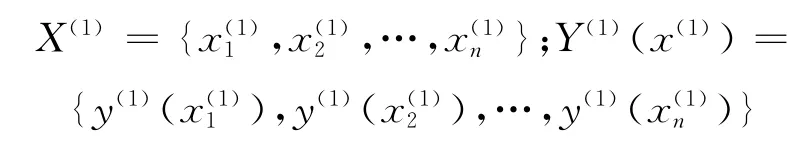

GM(1,1)模型的响应函数为:

式(2)为GM(1,1)灰色预测模型的具体计算公式,且参数-a和b分别为模型的发展系数和灰色作用量,其值由最小二乘法求出。式(2)的还原值如下:

1.2 灰色系统预测模型的精度检验
模型精度一般由均方差比值C和小误差概率p共同确定:

其计算方法和模型精度等级参考文献 [6]。模型精度等级分为Ⅳ级,Ⅰ级最好,Ⅳ级最差。
2 灰色预测模型的应用
氯代苯分子的20℃、15min条件下使发光菌发光强度减少1/2时的浓度EC50(mol/L)、大型蚤的24h半致死浓度LC50值取自文献 [8]、-lgKOW(正辛醇-水分配系数)、-lgSW(水中的溶解度)、表面积(100nm2)TSA、分子体积(100 nm3)V、摩尔质量(g/mol)M 和摩尔体积Vm(mL/mol)来自文献 [9]。相关数据及灰色综合关联度(ρ)计算[6]结果见表1。
灰色综合关联度的大小不仅反映了Y(0)与X(0)相关的程度,同时也反映出Y(0)随X(0)变化速率的接近程度。由表1可知-lgEC50或-lgLC50与-lgKOW的ρ最大,故将-lgKOW选择为氯代苯分子结构与生物活(毒)分析的灰变量。
2.1 灰色预测模型及其预测结果
将表1中9个或11个氯代苯分子的-lgEC50和-lgLC50分别与-lgKOW建模,其GM(1,1)灰色预测模型如下:
-lgEC50的灰色模型:

式(4)中,N、R2、SE、F和P依次为灰方程的样本数、判定系数、标准偏差、Fischer检验值和P显著性水平(下同)。
-lgLC50的灰色模型:


按式(4)和式(5)分别计算12多氯代苯-lgEC50或-lgLC50值、误差和平均值,以及文献的预测值、误差和平均值与实验值的比较列于表2中。

表1 氯代苯的化学结构参数及灰色综合关联度Table1 Chemical structure parameters andρof chlorinated benzenes

表2 氯代苯的-lgEC50或-lgLC50的计算值(或预测值)Table2 Calculated value-lgEC50or-lgLC50of chlorinated benzenes(predicted value)
2.2 模型精度检验
由表2中数据分别计算灰色模型(4)和(5)的S1、S2、均方差比值C和小误差概率p,计算结果见表2。由表2可见,灰色模型(4)和(5)均为Ⅰ级(优秀)。
3 结果与讨论
3.1 模型预测能力与可靠性检验
本文灰色模型的F值>105,P=0.05水平上的显著性检验<0.0005(本文P=0.0000),且都为单变量模型,因此模型从统计学的意义上讲也是成立的,模型真实可靠。采用式(4)预测了不在灰色集中的1,3-二氯苯、1,3,5-三氯苯和五氯苯 的-lgEC50值,分 别 为 4.27(4.24)、4.58(4.55)和5.81(5.69),其预测结果与括号中的实验值吻合程度好。因此,该灰色模型具有良好的预测能力和可靠性。
3.2 误差分析与其它模型的比较
根据表2的数据分别计算本文和文献 [8]的误差,其结果见表3。

表3 误差分析Table3 Error analysis
由表3可见,本文所建模型的误差均好于文献[8],可见建立的灰色模型优于文献 [8]的线性回归模型。
4 结 语
借助灰色系统理论来研究有毒化合物的生物活(毒)性预测,具有一定探索的性质,有待更加深入、更具体地研究。其次,目前大量有毒化合物的结构参数(如-lgKOW)被发表,为建立灰色模型预测有毒化合物的生物活(毒)性提供了方便,从而为判断有毒化合物的环境归宿和风险性评价有重要指导意义。
[1]王连生,韩朔睽.有机污染化学进展 [M].北京:化学工业出版社,1998:7-154.
[2]解静芳,郭炜锋.色谱保留指数在预测氯苯类和氯酚类化合物对戈卑鱼LC50中的应用 [J].环境与健康杂志,2005,22(6):441-444.
[3]堵锡华.修正的分子连接性指数mL用于氯代苯、醇、酯的QSAR/QSRR研究 [J].分析测试学报,2003,22(5):18-22.
[4]秦正龙.卤代芳烃对水生生物急性毒性的定量构效关系研究 [J].环境污染治理技术与设备,2005,6(1):50-53.
[5]谢武明,胡勇有,刘焕彬,等.持久性有机污染物的环境问题与研究进展 [J].中国环境监测,2004,20(2):58-61.
[6]刘思峰,党辉国,方志耕,等.灰色系统理论及其应用:第五版 [M].北京:科学出版社,2010.
[7]张 旭,谢修银.持久性有机污染物多氯联苯(PCBs)生物毒性的灰色理论研究 [J].长江大学学报:自然科学版,2009,6(1):41-43.
[8]周享春,赵元力,余训民.用氯代苯、烷基酚和醇类化合物气相色谱保留指数预测其生物活(毒)性 [J].北京工商大学学报:自然科学版,2004,22(4):9-14.
[9]杨海浪.W*对氯代苯类分子理化参数的应用研究[J].武汉科技学院学报,2004,17(3):67-71.
