高聚物黏弹性力学模型装置的研究
2013-07-06唐瑞敏任德财张艳红
谢 刚,唐瑞敏,任德财,张艳红
(1.黑龙江大学 化学化工与材料学院,哈尔滨 150080;2.黑龙江省有色金属地质勘探研究总院,哈尔滨 150046;3.黑龙江东方学院,哈尔滨 150086)
0 前 言
高聚物是一类黏弹性材料[1],在低温或特别快的作用时间下,材料表现为弹性;当在高温或特别慢的作用时间下,材料表现为黏性。然而在通常温度下或中等的加载时间内,材料同时具有弹性和黏性。从理论上可用理想的弹簧和黏壶以不同的方式组合,形象地模拟高聚物的黏弹性[2-4]。理想弹簧的弹性模量和黏壶的黏度只是在微分方程中代入参加运算,没有具体数值。理想弹簧和黏壶组成的各种力学模型,它们只是一种抽象的概念[5]。自行研制一台黏弹性力学模型装置,它可组合成不同的力学模型,通过实验可得到应力松弛曲线和蠕变曲线。根据以上两种曲线可以计算出实际弹簧的Ε值和实际黏壶的η值,把Ε和η代到对应的微分方程中可得到计算的蠕变曲线和应力松弛曲线。再把实验得到的蠕变曲线和应力松弛曲线与计算得到的蠕变曲线和应力松弛曲线进行对比,判断实际力学模型的精准性。
1 实验部分
1.1 实验装置
自行研制的高聚物黏弹性力学模型装置见图1。其工作原理是:由2个固定横梁4和4个拉杆6组成一个框架结构,3个活动横梁11可以在拉杆上做平行滑动,根据需要可以在活动横梁上装上不同的弹簧8,10和黏壶9,12,组成 Maxwell模型、Kelvin模型、3元件模型和4元件模型。在托盘1上加上砝码2通过定滑轮3产生一个水平力,水平力的大小可以通过测力计5显示,力学模型产生的形变可以通过应变仪7显示。
1.2 实验方法
首先将弹簧Ⅰ和黏壶Ⅰ串联,组成一个Maxwell模型,施加一个恒定形变(ε0),通过力学模型装置测出应力与时间的关系曲线(即应力松弛曲线),然后将弹簧Ⅰ和黏壶Ⅰ并联组成一个Kelvin模型,施加一个恒定的应力(σ0),通过力学模型装置测出应变与时间的关系曲线(即蠕变曲线),根据应力松弛公式[6]:

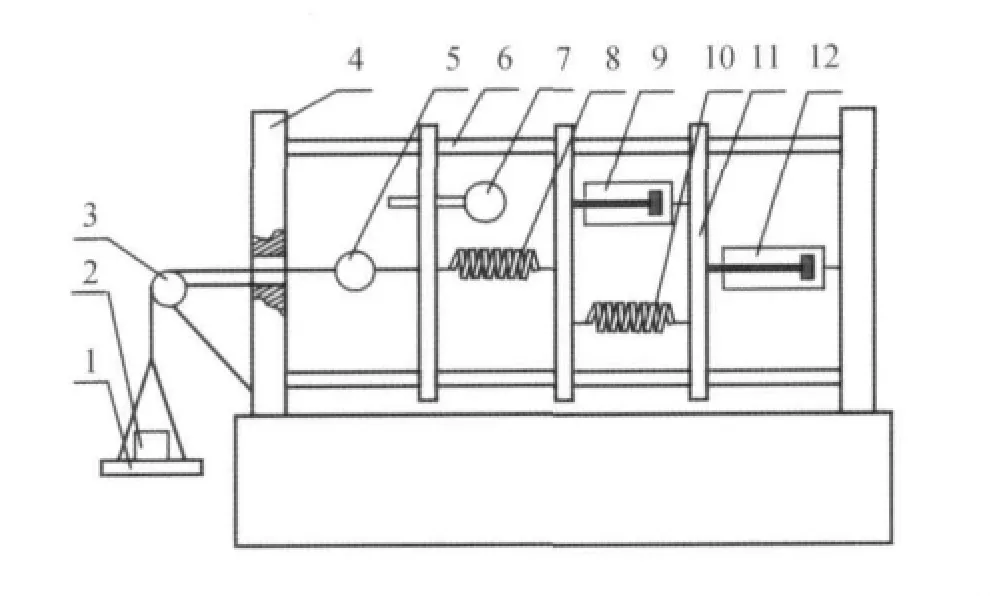
图1 力学模型装置示意图Fig.1 Schematic diagram of the device of mechanical model
式中Ε为弹簧的弹性模量;η为黏壶的黏度;t为作用时间。
根据蠕变公式:
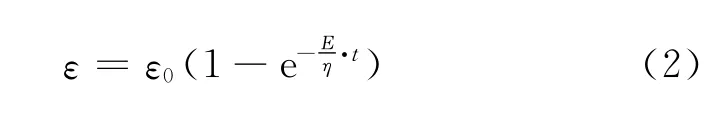
推导出弹簧的弹性模量公式:

式中σ(t)为某一时间的应力;ε(t)为某一时间的应变。
黏壶的黏度计算公式:

因此通过把实际的弹簧和黏壶分别进行串联和并联的方法,可以求得实际弹簧的弹性模量Ε1、Ε2和实际黏壶的黏度η1、η2。将4个元件的参数代入到4元件模型(four-element model)的蠕变公式:

代入不同的时间(t)即得到一个蠕变曲线,将计算得到的蠕变曲线与实验得到的蠕变曲线作对比,证明了力学模型装置是可以实现各种力学模型的受力和形变特点。
2 结果与讨论
2.1 Ε1和η1的测定
选取一个钢丝拉力弹簧作为弹性元件(弹簧Ⅰ),钢丝直径d1=1.54mm,中径 D1=17.16 mm,工作长度L1=260mm。选取一个黏壶作为黏性元件(黏壶Ⅰ),内径d2=19mm,工作长度L2=166mm,工作介质为牛顿型流体甘油。首先在力学模型装置上将两种元件串联,组成一个实际的Maxwell(a)模型,施加一个恒定的应变(ε0),经过测试得到一个应力松弛曲线,见图2。再将两种元件并联得到一个实际的Kelvin(a)模型,施加一个恒定的应力(σ0),经过测试,得到一个蠕变曲线,见图3。


由式(3)和式(4)计算并且经过算术平均得到:Ε1=1068.99MPa,η1=3013.66MPa·s。
2.2 Ε2和η2的测定
选取弹簧Ⅱ的钢丝直径d3=1.75mm,中径D2=18.78mm,工作长度L3=90mm。黏壶Ⅱ的内径d4=30mm,工作长度L4=136mm,工作介质为甘油。同样方法,两种元件串联时组成Maxwell(b)模型,得到的应力松弛曲线见图4。两种元件并联时组成Kelvin(b)模型,得到的蠕变曲线见图5。


经过计算平均得到Ε2=1299.80MPa,η2=77347.37MPa·s。

图6 4元件模型蠕变曲线Fig.6 Creep curve of four-element model
2.3 4元件力学模型的测定
将以上4个元件在力学模型装置上组成一个实际的4元件模型,测定其蠕变曲线,见图6。再将计算得到的Ε1、Ε2、η1、η2代入4元件力学模型的蠕变方程,代入不同的时间(t)得到一个计算蠕变曲线,见图7。
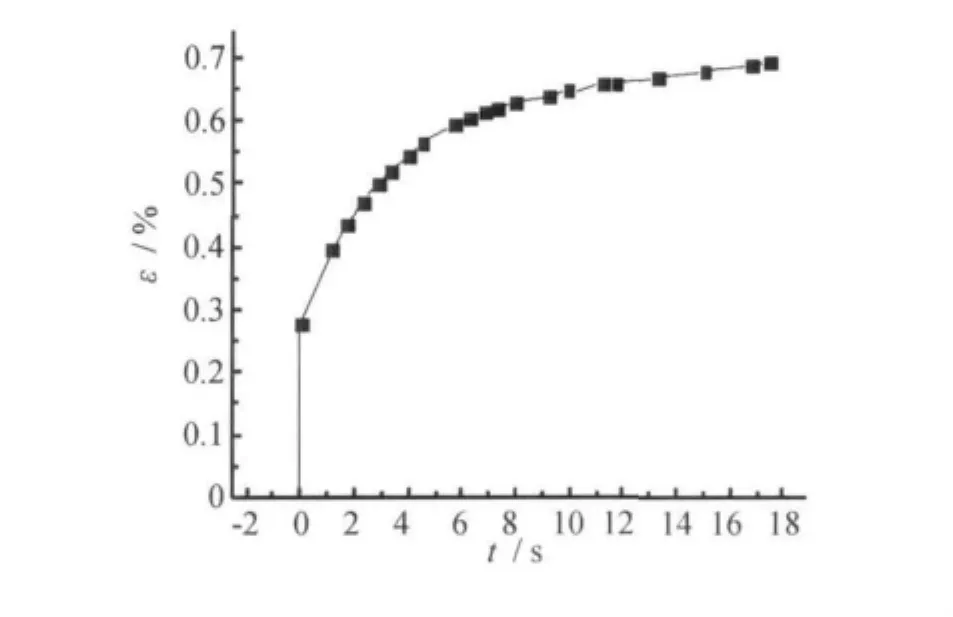
图7 理论计算的蠕变曲线Fig.7 Creep curve of theoretical calculation
将实验蠕变曲线与计算蠕变曲线相叠加对比见图8,由图8可见,两种曲线基本吻合,说明实际的弹簧和黏壶可以代替抽象的弹簧和黏壶,因此表明实际的、具象的力学模型可以代替经典的、抽象的力学模型。

图8 实验蠕变曲线与计算蠕变曲线叠加图Fig.8 Comparison chart of experimental creep curve and calculated creep curve
3 结 论
本文从一个全新的角度研究了高聚物黏弹性力学模型,通过理论推导和实验事实均证明了该力学模型装置能够较准确地反映高聚物的黏弹性的一些规律,并且证明了高聚物黏弹性力学模型不再是一个抽象的力学模型,而是一个具象的、可以实际应用的力学模型,实际弹簧的Ε值和实际黏壶的η值是可以计算得到的,为高分子科学理论与实用的研究提供一个新的平台。
[1]Chang D H.Rheology in prolymer processing [M].New York:Academic Press,1976.
[2]Ritchie P D.Physics of plastic[M].London:Iliffe Books Ltd.,1965.
[3]Leaderman H,Eirich F R.Rheology[M].New York:Academic Press,1960.
[4]Bernhardt E C.Processing of thermoplastic materias[M].New Jersey:Van Nostrand-Reinhold Press,1959.
[5]金日光.高聚物流变学及其在加工中的应用 [M].北京:化学与工业出版社,1986.
[6]何平笙.高聚物的力学性能 [M].合肥:中国科学技术大学出版社,1997.
