土石坝动力反应分析的阻尼模型及计算频率

迟世春，陶警圆，贾宇峰

（大连理工大学 建设工程学部 水利工程学院，辽宁 大连 116024）

0 引 言

阻尼是结构在振动过程中表征能量耗散特征的参数，对结构动力分析结果的可靠性和精度有很大影响。实际结构振动时耗能是多方面的，具体型式相当复杂，而且耗能不像构件尺寸、结构质量、刚度等有明确的、直接的测量手段和相应的分析方法，使得阻尼问题难以采用精细的理论分析方法，而是采用宏观总体表达的方法[1]。

结构振动时耗能的因素较多，但影响程度有所不同。一般认为振动过程中耗能因素有以下几方面：结构材料的内摩擦；连接处的干摩擦；空气阻尼；地基中波的辐射耗能等。当结构体系进入弹塑性状态时，构件的塑性耗能将远大于上述各项耗能。一般分析中不将塑性耗能纳入阻尼耗能，而是单独加以表达。对于松散颗粒集合体构成的土石坝而言，笔者认为，其耗能的主要部分是颗粒之间相对运动引起的干摩擦，在大震条件下颗粒破碎也消耗一定能量。其塑性耗能一般则纳入阻尼耗能加以考虑，除非采用动力弹塑性模型描述坝料，此时塑性耗能与阻尼耗能区分表达。

经过近100a的研究，已经提出了各种各样的阻尼表达方法，主要分为：黏滞阻尼和滞回阻尼（复阻尼）。黏滞阻尼假定阻尼力与速度成正比，无论对简谐振动还是非简谐振动得到的振动方程均是线性方程，不仅求解简便，而且能够方便地表达阻尼对频率、共振等的影响，是应用最为广泛的阻尼模型。通过将阻尼系数与结构体系的质量、刚度相联系，可以方便地构造出具体的阻尼系数，是目前最常用的阻尼表达方法；滞回阻尼则假定应力应变间存在一相位差，从而振动一周有耗能发生。已经提出了各种各样的滞回阻尼模型，其特点是得到不随频率改变的振型阻尼比。因而一般认为能较好地反映干摩擦为主的耗能机制形成的阻尼，但该模型在理论上只适用于简谐振动或有限频段内的振动分析。滞回阻尼还将导致复数形式的刚度，这对一般时程分析而言，计算复杂，因而复阻尼的实际应用并不多。

目前，在土石坝动力分析中的阻尼均采用黏滞阻尼模型。黏滞阻尼模型的最大优点是运动方程求解方便，缺点是实际计入阻尼与频率相关。阻尼的频率相关性会导致坝体动力分析中各阶振型实际计入的阻尼比不同，进而导致动力分析中某些频段的动力反应被人为抑制或放大，引起坝体计算动力反应的失真。

1 土石坝动力反应分析中的阻尼问题

在确定瑞利（Rayleigh）阻尼系数a0、a1时，根据振型正交条件[2]，有：

给定任意2个振型阻尼比，就能确定2个系数a0和a1。设给定的2个振型阻尼比为ζi和ζj，由上式得：

解上式，有：

这样，通过给定任意2阶振型的阻尼比ζi和ζj，由式（3）可以求出瑞利阻尼的2个系数a0、a1，再由式（1）则确定任意阶的振型阻尼比。绘出式（1）表示的阻尼比与频率的关系，见图1。

图1 Rayleigh阻尼比与频率的关系Fig.1 Relationship between Rayleigh damping ratio and frequency

工程计算中，一般取ωi＝ω1，即结构基频，而ωj则在对动力反应有显著贡献的高阶振型中选取。这样能够保证对应的这两个振型可以得到所需要的阻尼比，而在这两个指定频率之间的频率所对应的振型具有较低的阻尼比，相反频率＞ωj的振型阻尼比＞ζj，并随着频率增加振型阻尼比单调递增。这种情况将导致具有很高频率的振型反应因其高阻尼比而被有效地消除。因此，瑞利阻尼突出了给定振型和附近振型对结构反应的影响，对高阶振型的削减较为有效。当然，也有对两个采用频率之间的振型反应被人为放大的风险。

一般来讲，结构不同振型的阻尼比会有所不同，这是因为在结构的阻尼耗能主要为摩擦耗能的情况下，摩擦耗能取决于结构材料之间的相对位移，不同振型所表达的结构材料之间的相对位移并不同，因此每个振型的阻尼比也会有所不同。但在结构工程领域，目前公认的结论是，以上部结构为主的结构体系具有在相当宽的频率范围内振型阻尼比不变的特征。即认为ζi＝ζj＝ζ，则式（3）变为：

然而，在当前土石坝地震反应分析的阻尼计算中，没有区分不同频率的差别，统一取计算频率ω，即：

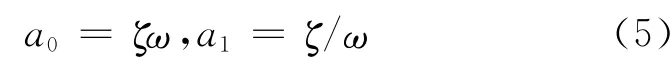
这样，计算频率的选取则成为问题的关键，目前大多取坝体基频作为计算频率。

日本学者曾对若干堆石坝实测第一周期，提出了堆石坝第一周期与坝高的关系[3]，冈本舜三提出的公式为：T＝（0.35～0.65）H／100；河上房义提出的公式为：，H为坝高。根据上述公式，坝高50m堆石坝的基本周期为0.175～0.325s。随着现代碾压技术的提高，堆石料被压实的更为紧密，堆石坝的基本周期还会减少。

地震的卓越周期是另一个影响坝体地震反应的重要因素。我国 《水工建筑物抗震设计规范》规定了设计反应谱及谱峰值对应的周期为 [0.1，Tg][4]，一、二、三、四类场地的Tg分别为0.2、0.3、0.4、0.65s。因此，对一般场地，坝高＜50m的低坝，其基本周期与地震卓越周期基本吻合。此时坝体第一振型的反应占优，坝体动力反应主要受第一振型以及附近的几阶低阶振型控制。此时，在瑞利阻尼计算中采用坝体第一周期对应的基频是合适的。

但对坝高达到300m级的高土石坝，情况则较为复杂。图2为300m高心墙堆石坝自振频率与基岩设计反应谱的对比。可以看出，坝体基本周期为1.712s，对应的谱值较小为0.32；而第7、8、9阶周期在0.1～0.2s之间，对应着反应谱的峰值。此时，地震作用坝体第一振型放大较小，而6～12阶振型放大较大。若再采用基频作为计算阻尼的唯一频率，显然6～12阶振型阻尼会被高估，进而低估高阶振型反应，得到的土石坝地震反应偏小，应用于设计则偏不安全。

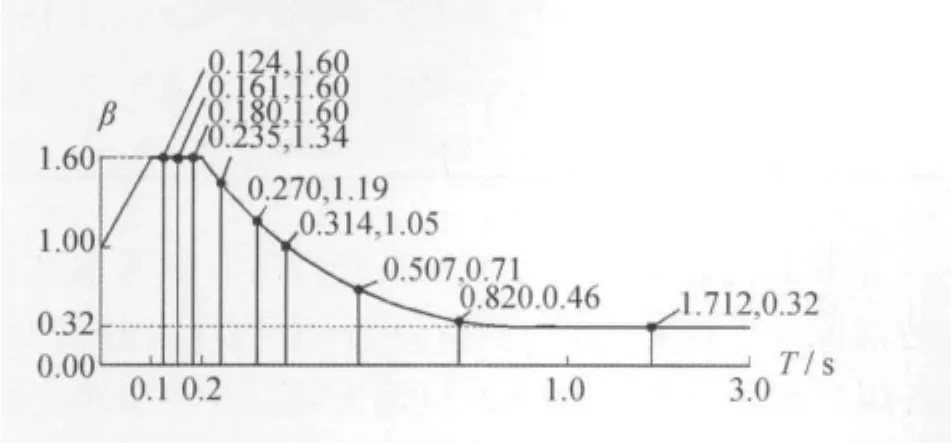
图2 基岩设计反应谱及300m堆石坝自振周期[5]Fig.2 Design response spectrum on bedrock and natural periods of 300mrockfill dam

同济大学楼梦麟教授提出了采用转换频率计算土石坝阻尼[6]。转换频率ωc是通过对多条地震波作用下地基土层的时域反应分析，并与频域结果比较，求取土层顶部绝对加速度最大值误差随阻尼系数转换频率变化曲线，以误差为零的频率为最佳拟合频率，对最佳拟合频率回归分析，得到阻尼系数转换频率的经验公式[7]，由转换频率代替基频进行阻尼计算。该方法综合考虑了地震波的频谱特性和地基土层的特性，但由于是针对地基土层，是否适合土石坝不得而知。

Idriss等提出了一种采用2个频率来确定阻尼系数的新方法[8]，即ωi＝ω1，ωj＝nω1。ω1为基频，n为＞ωe／ω1的奇数，其中ωe为地震波的主频。也可直接取ωj为地震的卓越频率ωp，或将ωj取为输入地震波Fourier谱的重心处频率ωg，以作为阻尼计算的改进。

2 不同阻尼模型的土石坝地震反应

本文采用瑞利阻尼模型，但其计算频率取以下5种情况，见表1。分别进行了坝高为50，100，150，200，250，300m的6种心墙堆石坝的地震反应分析计算。坝体的上、下游坝坡均取1∶2.0，心墙上、下游面坡度均为1∶0.2。为简化计算，坝体仅考虑堆石料和心墙料两种坝料。静力计算采用邓肯E-B模型，计算参数见表2。

表1 确定Rayleigh阻尼系数的5种方法Table1 Five methods to determine the Rayleigh damping parameters

表2 邓肯E-B模型参数Table2 Parameters of Duncan E-B model

土石坝动力计算，最大动剪模量采用：

式中C，n分别为最大动剪模量系数和指数；Pa为大气压力。

堆石料C＝2455、n＝0.6，心墙料C＝1688，n＝0.464。

坝料模量衰减和阻尼增长曲线按照笔者等统计的国内外筑坝土石料试验曲线的拟合公式[9]：

式中b为动剪模量比衰减曲线在动剪应变幅γ在10－6～10－1之间时的最小值；x0为曲线拐点值，调整曲线在应变轴上的位置；m为指数；A1、A2为阻尼比增长曲线在动剪应变幅γ在10－6～10－1之间时的最小值和最大值；α为系数，调整曲线在应变轴上的位置；n为指数。

堆石料和心墙料的上述参数见表3。

采用规范谱人工地震波输入，拟合设计反应谱参数为βmax＝2.0，Tg＝0.3s，峰值加速度Amax＝0.2g，地震持时为24s。人工地震波加速度时程曲线及其Fourier谱见图3。

表3 动模量与阻尼曲线参数Table3 Parameters of dynamic modulus and damping

图3 人工地震波加速度时程曲线及其Fourier谱Fig.3 Acceleration time history and Fourier spectrum of artificial seismic wave

表4列出了各阻尼模型下不同坝高的坝顶最大加速度。由表4可见，与频域解比较采用传统阻尼模型1时坝高＞100m则坝顶加速度均被低估，且低估程度也随着坝高的增加而增大。

采用模型2计算的坝顶加速度略偏低，但较模型1有改进。模型3和模型5计算的坝顶加速度反应明显偏大，这说明Idriss方法确定的频率或以Fourier谱重心频率作为阻尼计算频率ωj偏大，使得ωi和ωj之间的较多阶振型的振型阻尼比被低估，总体加速度反应明显偏大；由模型4的计算结果可见，采用地震波卓越频率和坝体基频来进行计算时，加速度反应略微偏大。

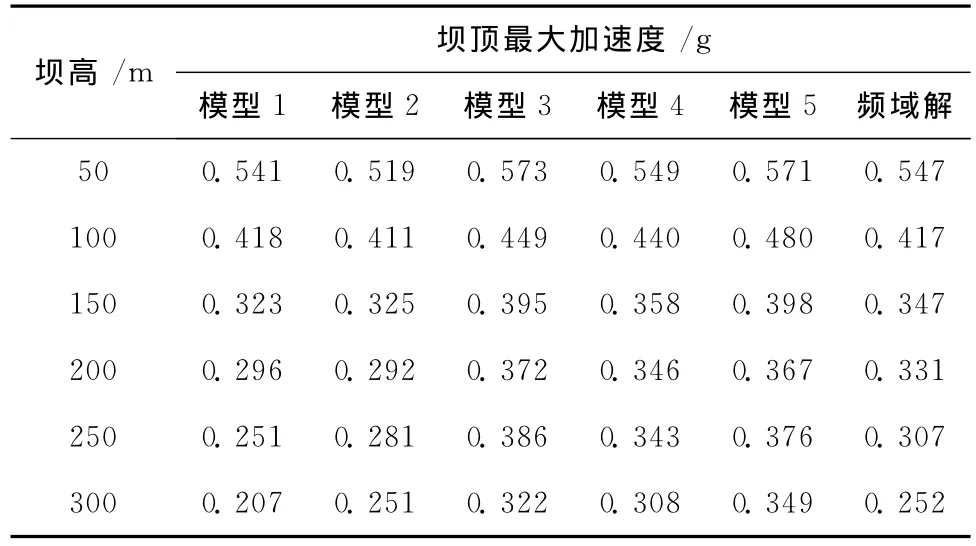
表4 不同阻尼模型下坝顶最大加速度Table4 Peak acceleration at dam crest under different damping models

由上述分析可见，当坝高较低时，仅考虑结构的自振频率计算阻尼是可行的，但当坝高较高时，各阻尼模型计算的坝体反应偏大或只在少数坝高处与频域解接近。

3 地震输入对阻尼计算频率的影响

在目前的土石坝动力计算中，阻尼模型一般采用式（5）计算阻尼。选用的计算频率不同，动力分析的结果也不同。因为在计算频率（即坝基频）处，对应着材料的实际试验阻尼，在阻尼频率曲线上却为最小值，见图4。这样，在其它高阶振型的频率处坝体实际计入的阻尼会高于坝料的实际阻尼。如果计算频率附近的振型反应占坝体结构反应的绝大部分，则动力反应分析成果是可以接受的。因为占绝大部分的坝体反应采用了合适的阻尼。

因为坝体反应与输入地震的频谱特性有关，为此需要研究输入地震的频谱特性与阻尼计算频率的关系。根据 《水工建筑物抗震设计规范（DL5073-2000）》的设计反应谱及4类场地的特征周期Tg＝0.2，0.3，0.4，0.65s，拟合了4条规范谱人工地震波，见图5。4条地震波的最大峰值加速度Amax＝0.2g，βmax＝2.0，地震持时均为24s。

图4 阻尼比与频率关系曲线示意图Fig.4 Schematic diagram of damping ratio vs.frequency

图5 不同特征周期的规范谱人工地震波Fig.5 Acceleration time history of artificial seismic wave with different characteristic period

采用阻尼公式（5），计算了不同特征周期规范谱人工波作用下6种坝高心墙堆石坝的动力反应，绘制了坝顶最大加速度反应与阻尼计算频率的关系曲线，见图6。

由图6可见，阻尼计算频率、坝高及反应谱特征周期对坝体反应的影响均较大。输入地震波的目标反应谱分别采用4种特征周期，6种坝高的坝顶最大加速度反应与阻尼计算频率曲线的差别也较大。显然，确定阻尼计算频率需考虑坝高和地震输入两个因素，也就是应当考虑坝体的自振特性及输入地震波频谱特征的共同影响。

以300m高心墙堆石坝为例，分析输入地震波目标谱特征周期对坝体最大加速度反应的影响。图6（a）中当阻尼计算频率＞7rad／s后，坝顶最大反应对计算频率并不敏感，说明对位于近震基岩场地上300m级的高土石坝，阻尼计算频率可取大于坝体2阶频率7.45rad／s的任何数值，对坝体反应的影响均不大；而图6（b）、图6（c）、图6（d）中坝高300m时的曲线显示，坝体反应受计算频率影响大，因此对远震深厚覆盖层上的坝，阻尼计算频率对坝体反应的影响较大，需要研究坝高及地震频谱特性的影响后再行确定较为妥当。

根据图6，查出坝顶最大加速度曲线取得极值时的阻尼计算频率，见表5，并将该频率对应的坝体自振频率阶数范围也列入表中。由表5可见，坝高为50m时，坝顶最大反应对应的阻尼计算频率较一致，且与该土石坝的基频接近。而坝高100m及其以上的坝体，随着输入地震动的频谱特性的不同，坝顶最大加速度曲线的极值频率及其对应的阶数有较大差异。若以最大加速度反应为预测目标，则特征周期较长时，宜应采用相对较小的频率；反之则采用较大的频率计算阻尼。

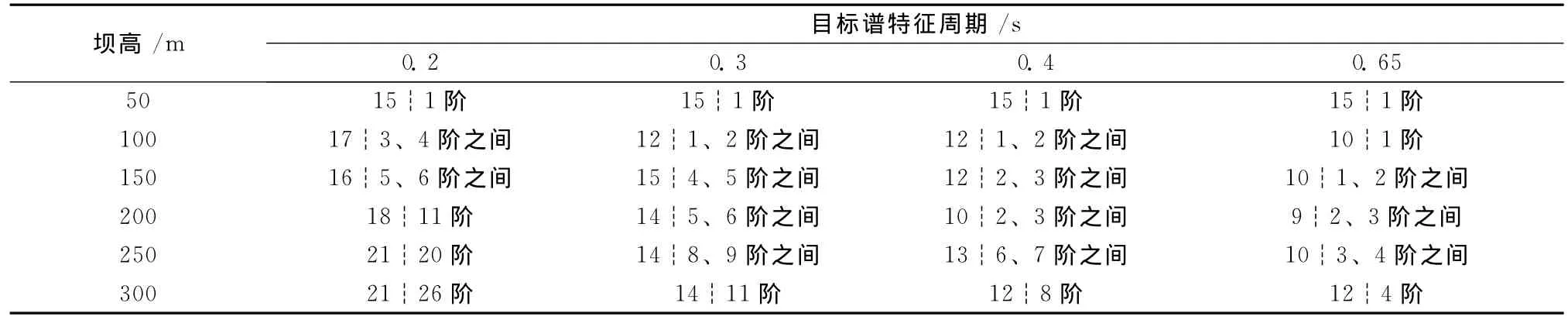
表5 坝顶加速度最大值时的阻尼计算频率及其对应的坝体自振频率阶数Table5 Control frequency in damping calculation and corresponding model number for free vibration of dam when acceleration of dam crest gets maximal value ／rad·s－1

因此，地震频谱特性对坝体的动力响应有较大影响，在选择阻尼模型和确定阻尼系数时，如果不充分考虑到这一点，很可能会低估或高估阻尼的作用，从而导致计算得到的动力响应不合理。

4 高阶自振频率阻尼模型

瑞利阻尼模型采用式（4）的两个控制频率计算，但ωi与ωj也可均取高阶自振频率，具体取法见表6，进行坝体动力有限元分析，得到坝顶最大加速度反应列入表7。

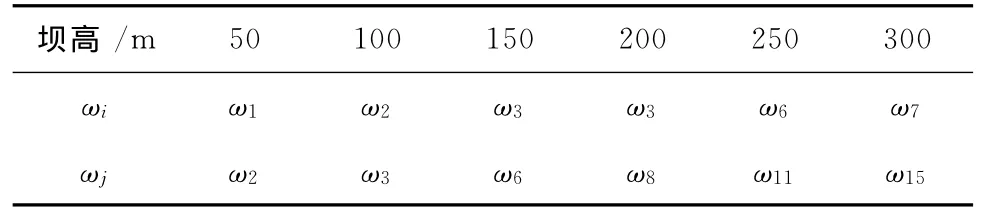
表6 高阶自振频率阻尼模型Table6 Damping model for high model frequencies of free vibration

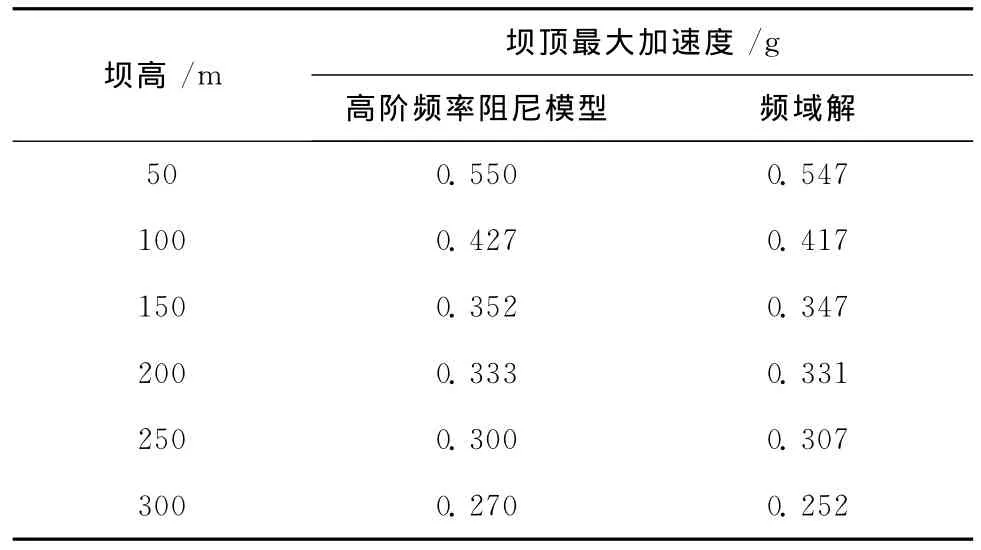
表7 高阶频率阻尼模型与频域解的坝顶最大加速度Table7 Dam crest accelerations under new damping model

由表7可见，坝顶最大加速度反应与频域解接近，较前面讨论的几种阻尼方法有所改进，随着坝高的增加，坝体的加速度反应并不会被低估。因此，阻尼模型计算频率均取高阶振型频率也是不错的选择。

5 结 论

目前土石坝地震动力反应分析一般采用瑞利阻尼模型，其计算频率取坝体基频。但瑞利阻尼模型实际计入结构动力分析的振型阻尼比与计算频率有关，其特点如下：在计算频率附近实际计入的振型阻尼比等于材料的试验阻尼比；在2个计算频率之间则小于材料阻尼；在2个计算频率以外则高于材料阻尼。通常只采用基频计算瑞利阻尼系数，则除基频点外实际计入的阻尼均高于实际材料阻尼。

对坝高相对较低的土石坝而言，只采用基频的阻尼模型其计算精度是可接受的。这是因为50m左右的土石坝基频与基岩上地震卓越频率相近，基频附近的振型在动力反应中占优，而高阶频率成分的反应很小，即使高阶振型阻尼稍高对坝体动力反应的影响也非常有限。但对高土石坝则不然，300 m级高坝的基频很低，周期较长，动力反应中占优的振型在6～12阶左右，若再采用基频作为计算阻尼的唯一频率显然会高估动力反应中主要振型的阻尼比进而地震得到的坝体反应偏小，应用于设计则偏不安全。

解决问题的思路是采用2个频率控制的瑞利阻尼模型。阻尼计算频率的选择要考虑坝体自振特性和输入地震波的频谱特性影响。但对近震基岩场地上的300m级高土石坝，阻尼计算频率可取＞2阶频率即可，其它场地或坝高时，计算频率的选取需进行相关研究后确定。

[1]董 军，邓洪洲，王肇民.结构动力分析阻尼模型研究 [J]，世界地震工程，2000，16（4）：63-69.DONG Jun，DENG Hong-zhou，WANG Zhao-min.Studies on the damping models for structural dynamic time history analysis [J].World Information on Earthquake Engineering，2000，16（4）：63-69.（in chinese）

[2]R.W.Clough，J.Penzien.Dynamics of structures[M].New York：McGraw-Hill，Inc.，2003.

[3]迟世春.高面板堆石坝动力反应分析和抗震稳定分析方法 [D].南京：河海大学，1995.CHI Shi-chun.Dynamic response analysis and seismic slope stability analysis method of high concrete face rockfill dams[D].Nanjing：Hohai University，1995.（in chinese）

[4]DL 5073-2000，水工建筑物抗震设计规范 [S].DL5073-2000Specifications for seismic design of hydraulic structures [S].（in Chinese）

[5]张 锐.高土石坝地震作用效应及坝坡抗震稳定分析研究 [D].大连：大连理工大学，2008.ZHANG Rui.Analysis and research of seismic effects and slope seismic stability of high earth and rockfill dams[D].Dalian：Dalian University of Technology，2008.（in Chinese）

[6]楼梦麟，殷 琳.关于高土石坝地震反应分析中的阻尼模型的讨论 [J].水利发电学报，2009，28（6）：103-107.LOU Meng-lin，YIN Lin.Discussion on damping models for seismic response analysis of high earth dams[J].Journal of Hydroelectric Engineering，2009，28（6）：103-107.（in Chinese）

[7]楼梦麟，潘旦光.滞后阻尼在土层时域分析中的应用[J].同济大学学报，2004，32（3）：281-285.LOU Meng-lin，PAN Dan-guang.Hysteretic damping application in time domain analysis of soil layer [J].Journal of Tongji University，2004，32（3）：281-285.（in Chinese）

[8]邹德高，徐 斌，孔宪京.瑞利阻尼系数确定方法对高土石坝地震反应的影响研究 [J].岩土力学，2011，32（3）：797-803.ZOU De-gao，XU Bin，KONG Xian-jing.Study of influence of different methods for calculating Rayleigh damping coefficient on high earth-rock dam seismic response [J].Rock and Soil Mechanics，2011，32（3）：797-803.（in Chinese）

[9]迟世春，陈崇茂，张宗亮.土石坝料动力试验数据的一种统计公式 [J].水利与建筑工程学报，2011，9（6）：5-8.CHI Shi-chun，CHEN Chong-mao，ZHANG Zong-liang.A statistical formula for test data about dynamic characteristics of earth-rock dam materials [J].Journal of Water Resources and Architectural Engineering，2011，9（6）：5-8.（in Chinese）