可换环上一类不可解矩阵代数的导子
2013-07-05张波
张波
(淮北师范大学 数学科学学院,安徽 淮北 235000)
可换环上一类不可解矩阵代数的导子
张波
(淮北师范大学 数学科学学院,安徽 淮北 235000)
在含有单位元的交换环上构造一类不可解矩阵代数,并在其上定义内导子和置换导子.决定了这一类矩阵代数的所有导子,给出其上的每一个导子都可以分解成一个内导子和一个置换导子的直和形式.
矩阵代数;导子;直和
设R是一个含单位元的交换环,n是正整数,Rn是R上n元行向量的集合,Rn×n是R上n×n阶矩阵的全体,E表示n阶单位阵.
设X是一个R-代数,ϕ:X→X是一个R-模同态,且对任意的x,y∈X,都有
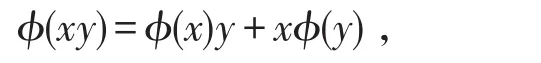
则称ϕ是R-代数X的一个导子.以DerX表示R-代数X上的导子的全体.
王登银[1-2],曹佑安[3]和Jøndrup[4]发表了一系列文章,研究含单位元的交换环上矩阵代数的导子和自同构问题.本文讨论了含单位元的交换环上的一类不可解矩阵代数的全部导子.



[1]WANG Dengyin,YU Qiu,OU Shikun.Derivations of certain lie algebras of upper triangular matrices over commutative rings[J].数学研究与评论,2007,27(3):474-478.
[2]WANG Dengyin,YU Qiu.Derivations of the parabolic subalgebras of general linear Lie algebra over a commutative ring[J].Linear Algebra Appl,2006,418:763-774.
[3]CAO Youan,TAN Zuowen.Automorphisms of the Lie algebras of strictly upper triangular matrices over certain commuta⁃tive rings[J].Linear Algebra Appl,2003,360:105-122.
[4]JøNDRUP S.Automorphisms and derivations of upper triangular matrix rings[J].Linear Algebra Appl,1995,221:205-218.
Derivations of an Unsolvable Matrix Algebra over a Commutative Ring
ZHANG Bo
(School of Mathmatical Sciences,Huaibei Normal University,235000,Huaibei,Anhui,China)
An unsolvable matrix algebra over a commutative ring with identity is constructed,and the inner derivation and permutation derivation are defined in this paper.An explicit description of the derivations of this matrix algebra is given,that is,each derivation can be represented to an expression of direct sum of an in⁃ner derivation and an permutation derivation.
matricx algebras;derivations;direct sum
O 152
A
2095-0691(2013)04-0023-03
2013-05-09
安徽省高校自然科学基金项目(KJ2009B082Z);淮北师范大学青年科研基金项目(700276)
张 波(1977- ),男,安徽萧县人,讲师,硕士,主要从事代数方面的研究.
