智能天线信号DOA估计中MUSIC算法的应用

梁勇

（河南大学物理与电子学院，河南 开封 475004）

智能天线信号DOA估计中MUSIC算法的应用

梁勇

（河南大学物理与电子学院，河南 开封 475004）

对智能天线进行了简要阐述，并对DOA估计的应用进行了介绍，就智能天线中相干信号采用MUSIC算法及其修正、改进方法进行DOA估计研究进行了分析。通过详细论证及相应的模拟仿真实验验证，表明所推介的两种基于经典MUSIC算法的修正和改进算法在DOA估计的相关方面有一定的优越性，从而可以为DOA估计的应用提供参考。

智能天线；相干信号；MUSIC算法；DOA估计

智能天线是将先进的信号处理技术应用在天线阵列中，使其具有空、时处理能力。具体通过对每个阵元进行自适应的幅度、相位调节，最后合并天线阵列完成其空域、时域处理能力。

空时处理技术很大程度上通过阵列信号处理来完成，其中空概念的提出标志着阵列信号处理的应用达到了一个崭新的层次。阵列信号处理的具体实施是通过在空间布置传感器阵列，通过对信号的接收、滤波、增益等提取包括方向、数目、频率等信号源对应信息。DOA估计作为空间谱估计技术一个分支在近年来得到了飞速发展，其目的是要实现入射空间信号角度的估计精度、分辨率的提高以及优化实现此目的各种算法[1]。

智能天线技术通过使天线波束变窄、增益扩大，同频干扰减少，频谱效率提高等技术可以在基站数量不变的情况下达到信号质量改善、系统容量扩大、设施性能增强等目的。通过智能天线技术的扩展可以突破目前蜂窝通信的移动台位置粗略划定，达到对持机者的实时准确定位，可用于开发一系列新业务。

智能天线通过以下方面的优越性在未来的通信系统中发挥作用[2]：

（1）在传统的通信系统中，信号一般经过反射、折射及散射完成传输过程，这其中信号的瞬时变化及延迟失真会不可避免的造成信号衰落，而智能天线可以控制波束的接受方向，达到减小延迟、控制衰落的目的；

（2）基于智能天线波束的方向性可将其与无线电波分离开来，从而屏蔽电波传播环境和优化天线阵列，实现空间滤波；

（3）智能天线还可以有效减小系统中出现的中断、切换、误码等问题，实现动态分配信道，增大发射功率，消除多址干扰，提高系统容量的目的。

智能天线分为DOA估计和波束形成两个环节；其中DOA估计是要对天线阵列的接收信号进行来向判断，针对波来方向形成波束并发射到预期方向。本文将对DOA估计算法进行详细论证分析。

1 相关信号源模型[3]

在实际情况中，由于多径传播或电磁干扰等因素的影响，存在大量相干信号源，而基于其建立的检测与估计也是DOA估计的重要组成部分，两个信号之间[Si(t),Sk(t)]的相关性可以用相关系数表示，如式(1)所示：

由以上分析可知，只要有一个基础信源S0(t)，即可生成n个相干信号源，如式（3）表示：

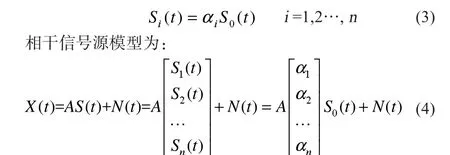
在实际环境中，当多信号之间完全相干时，信号子空间维数骤减并向噪声子空间“扩散”，致使两者不完全正交，为来波方向估计带来困难。

2 MUSIC算法介绍

MUSIC算法是基于多重信号分类进行的，当处理非相关信号源时具有复杂度适中，分辨率较高，估计误差较小等特点；但当信号相关度很高时会引起很大程度的秩亏损，从而造成其估计精度下降。理论研究中一般通过修正、改进、处理、变换等方法补偿秩亏损来进行解相干操作。

本文将在以下章节分别介绍常规及改进、修正后的MUSIC算法，并通过进行模拟仿真实验进行对比，验证其修正后的优越性能。

2.1 常规MUSIC算法[4]

常规MUSIC算法通过对天线阵列接收数据的协方差矩阵进行特征分解，根据分别得到的信号子空间和噪声子空间之间的正交性判断来进行信号DOA估计。算法的示意描述图如下，图1中1－M所示斜线为M个天线组成的均匀直线阵列，d为天线间距，βi为入射角(i=1,2, N)，设来波个数为N，波长为ξ，用式(5)表示。

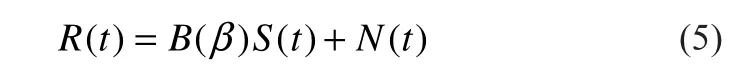
式中：R(t)为数据向量；N(t)为高斯白噪声；S(t)为空间入射信号，其值为[s1(t),s2(t), sN(t)]T；B(β)为阵列导向向量，其值为[b(β1),b(β2), b(βN)]。

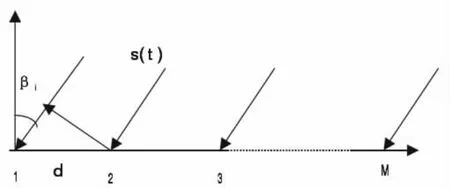
图1 算法示意图

阵列接收数据的协方差矩阵表示为：

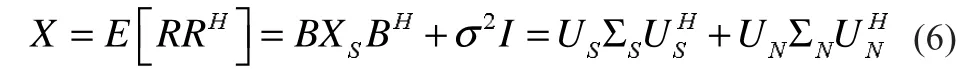
式中：Xs为空间信号协方差矩阵，其值为E[SSH]；σ2为噪声功率；US为信号子空间；UN为噪声子空间。

天线阵列接收数据协方差矩阵的最大似然估计为：

MUSIC算法实现波达方向估计公式为：

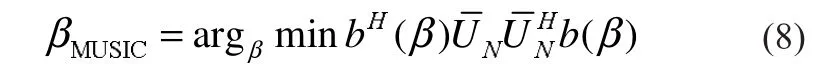
MUSIC算法中用于谱峰搜索的公式为：

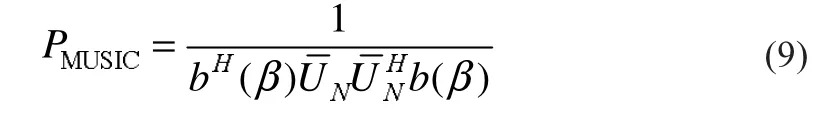
2.2 时间平滑MUSIC算法[5]

移动通信环境中，时间选择信道衰落程度用相干时间来表示，如式（10）所示：

式中：c为电磁波传播速率；υ为终端移动速率；fc为载波频率。由于移动在低速移动用户的信号传输中，波径的DOA基于移动台和基站间距变化幅度较小，但包括相位在内的复衰落向量变化较快。在同一传播路径的多个数据块中，当其持续时间＞tωh时，则判定其多径衰落不相关。

在天线阵列接收信号的过程中，第j个时间段内接收信号表示如式（11）：

3 模拟仿真实验

3.1 基于四阶累积量和时间平滑MUSIC算法的DOA估计[7]

本小节采用DOA估计联合算法，通过四阶累积量将多径信号按相干性和用户进行划分，利用时间平滑MUSIC算法进行相干多径信号的DOA估计。

根据前述理论分析，利用计算机仿真模拟实验进行算法验证。表1为模拟仿真实验1条件。

表1 模拟仿真实验1条件

实验1：

运用ArcGIS 10.2进行高低聚类分析，得出如图1所示商品住宅价格高低聚类图。从图中可以看出中山区、西岗区和沙河口区的大部分住宅价格以高高聚集为主，甘井子区住宅价格主要为低低集聚为主。高低聚集区主要分布在中山区北部和西岗区一小部分住宅。

目的：验证本小节方法在多径分量与用户配对方面的应用。

步骤：选取共信道用户对应1直射径和2条相干多径，对应DOA分别为－30°,10°,40°，进行传统前后向空间平滑算法和本小节算法的DOA估计。

结果分析：根据如图2所对应的传统前后向空间平滑算法和图3所对应的本小节联合算法仿真结果进行分析可以得出，两种方法都能够进行多径DOA准确估计，但就多径分量与用户配对方面来说，而本小节算法可以有效准确地实现配对与分组。

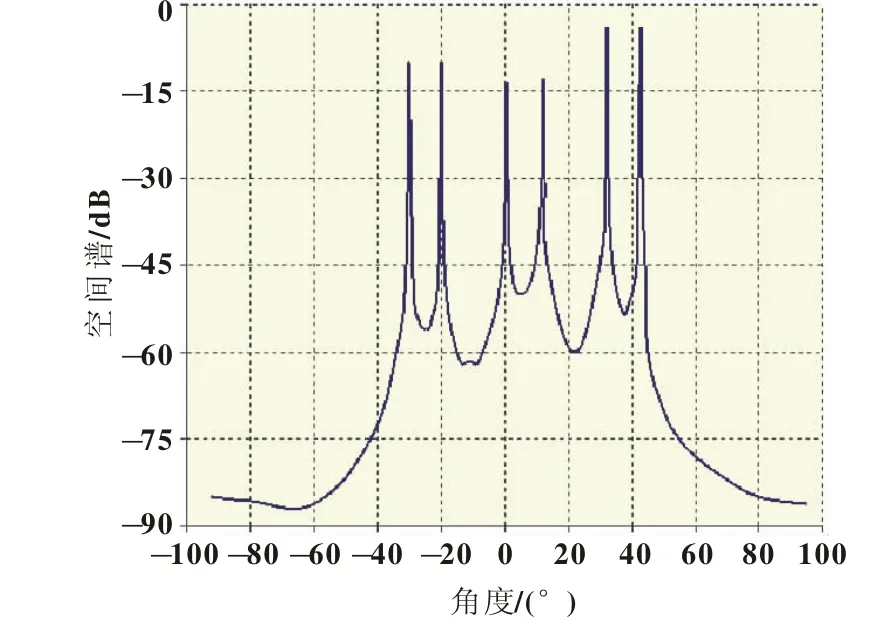
图2 应用传统前后向空间平滑算法的DOA估计

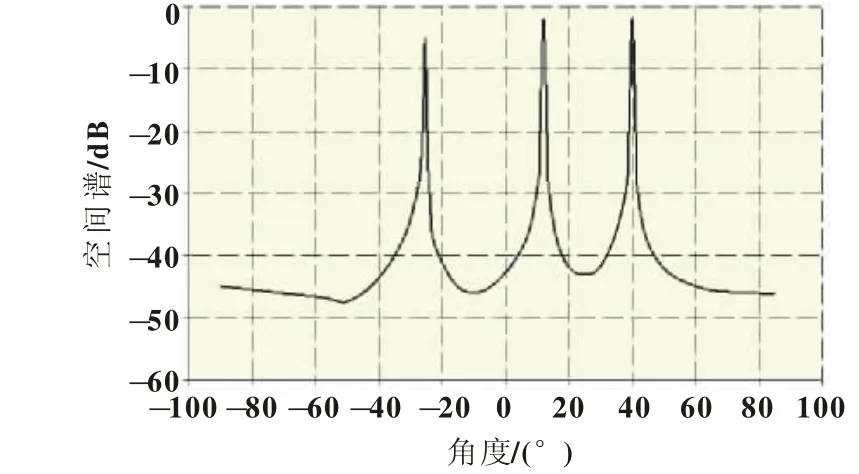
图3 应用本小节算法的DOA估计

实验2(实验2条件见表2)：

目的：分析DOA估计RMSE与快拍数和SNR关系。

步骤：选取共信道用户对应1直射径和2条相干多径，对应DOA分别为－30°,10°,40°，进行传统前后向空间平滑算法和本小节算法的蒙特卡洛实验。

表 2 模拟仿真实验2条件

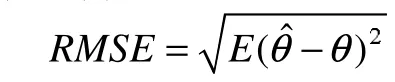
从图4(a)中的RMSE仿真结果可以看出RMSE随信噪比升高而减小，在同一信噪比下，本小节联合算法对应的RMSE值小于传统前后向空间平滑算法。从图4(b)中的RMSE仿真结果可以看出随快拍数的增加RMSE逐渐减小，在同一快拍数下，本小节联合算法对应的RMSE值小于传统前后向空间平滑算法。图4 R MSE仿真结果

3.2 基于矩阵重构的修正MUSIC算法的DOA估计[8]

本小节采用基于矩阵重构的修正MUSIC算法，通过协方差矩阵的重构降低信号间相关系数，以期提高对波达方向的辨识能力。表3为模拟仿真实验1条件。

结果分析：RMSE定义为：

表3 模拟仿真实验1条件

实验1：

目的：验证本小节方法在估计精度方面较常规修正MUSIC算法的优越性。

结果分析：从图5的仿真结果可以看出常规修正MUSIC算法在－1.5°时估计信号开始紊乱模糊，而本小节所推方法仍可以较为精确清晰地做出识别。可见对于极小间隔的相干信号，本小节推介的基于矩阵重构的修正MUSIC算法有其优越性。

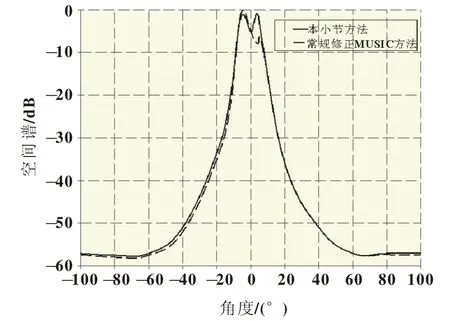
图5 小间隔相干信号的DOA估计

实验2(实验2条件见表4)：

目的：分析比较本小节方法在不同信噪比条件下DOA估计的偏差和成功率。

表4 模拟仿真实验2条件

步骤：为两相干信号的设置相同信噪比，使其从10～20 dB均匀变化，进行蒙特卡罗实验。选择－1.5°信号方向作为比较点。

结果分析：图6和图7所示分别为两种算法随信噪比变化的估计偏差和成功概率。经过分析可以得知，本小节推介的算法比常规修正的算法偏差率更小、成功率更高。

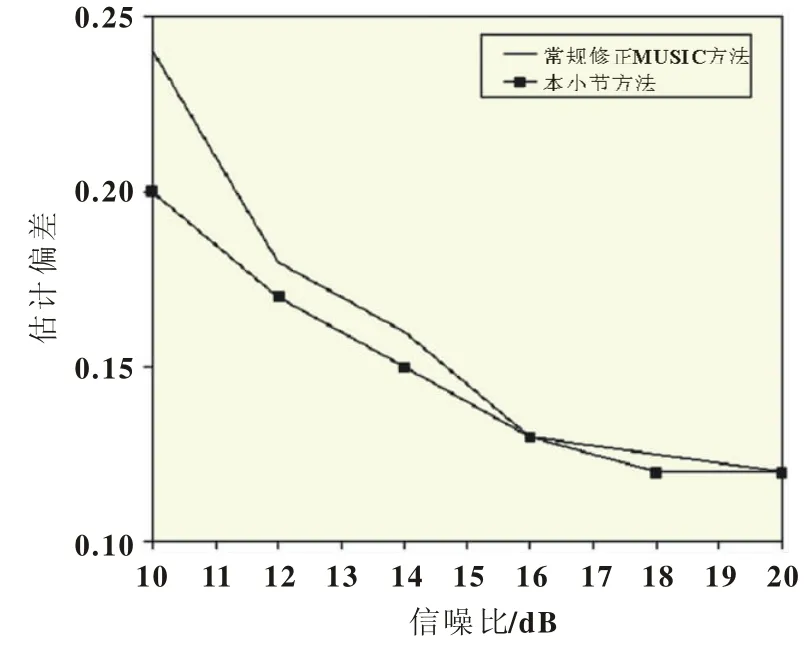
图6 随信噪比变化的DOA估计偏差

实验3：

目的：分析比较本小节方法在不同采样次数条件下DOA估计的偏差和成功率。

步骤：为两相干信号的设置取样点数200～500，以间隔50变化，进行蒙特卡罗实验。选择－1.5°信号方向作为比较点。

结果分析：图8和图9所示分别为两种算法随采样点数变化的估计偏差和成功概率。经过分析可以得知，本小节推介的算法比常规修正的算法偏差率更小、成功率更高。

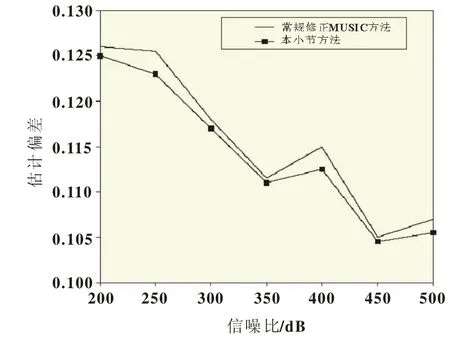
图8 随采样次数变化的DOA估计偏差

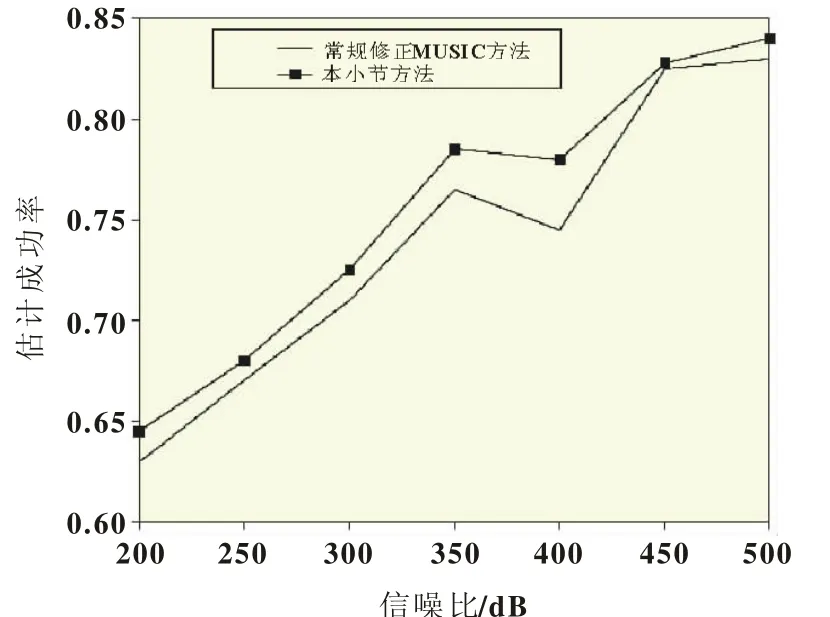
图9 随采样次数变化的DOA估计成功率

4 总结

本文首先对智能天线及DOA估计的应用进行了简要阐述和介绍，接着就智能天线中相干信号采用MUSIC算法及其修正、改进方法进行DOA估计研究分析。通过详细论证及相应的模拟仿真实验验证，表明本文所推介的两种基于经典MUSIC算法的修正和改进算法在DOA估计的相关方面有一定的优越性，从而可以为DOA估计的应用提供参考。

本文进行的讨论都是以白噪声为基础的，而实际中噪声类型很多，需要进行分开讨论；本文的模拟实验是基于少数信号进行的，而实际中信号源多而复杂，需要更多实时有效的DOA算法来解决实际问题；本文中所采用的均为窄带信号，而实际中其余类型的信号应用更为广泛，因此多数情况下需要算法之间的联合进行DOA估计；本文只对MUSIC算法进行了小范围的讨论，实际应用中的估计算法多种多样，其改进、修正算法也层出不穷，因此需要对各种方法进行综合权衡，选用合适的方法应用在通讯信号的DOA估计当中。

[1] 刘祎.智能天线中相干信号的波达方向估计[D].上海：上海师范大学，2009.

[2] 乐兵兵，吴多龙.一种新的去强相关信号方法的波达方向研究[J].电子设计工程，2012(3)：46.

[3] 刘兆霆，阮谢永.色噪声背景下基于声矢量阵列孔径扩展的相干目标波达方向估计[J].兵工学报，2011(3)：27.

[4] 胡增辉，朱炬波.基于联合对角化的远场相干信号波达方向估计[J].国防科技大学学报，2011(4)：33.

[5] 杨华.智能天线下的波达方向估计研究[D].大连：大连理工大学，2007.

[6] 窦凤辉.智能天线中波达方向估计算法的研究[D].西安：西安科技大学，2007.

[7] 景小荣，隋伟伟.基于四阶累积量和时间平滑的相干信号DOA估计[J].系统工程与电子技术，2012(4)：22.

[8] 田军华.波达方向估计以及在无线定位中的应用[D].大连：大连理工大学，2009.

Smartantenna signalDOA estimation using MUSIC algorithm

LIANG Yong
(School of Physicsand Electronics,Henan University,Kaifeng Henan 475004,China)

Smart antenna was introduced,and the application of DOA estimation was also described.The smart antenna coherent signals using MUSIC algorithm and its amendments,improved methods for DOA estimation was analyzed. Through a detailed demonstration and simulation experiments, the results show that the two referred certain advantages based on the classic MUSIC algorithm correction and improved algorithm in DOA estimation can provide a reference for DOA Estimation application.

smart antenna;coherent signals;MUSIC algorithm;DOA estimates

T M 645

A

1002-087 X(2013)11-2047-04

2013-04-15

梁勇（1972—)，男，河南省人，讲师，主要研究方向为EDA技术（FPGA）、单片应用、无线通信技术、测量技术，电子线路。