一种MH/Ni动力电池模型及其SOC预测方法

刘国繁，骆 晶

(1.湖南工程学院电气信息学院，湖南 湘潭 411104；2.湘潭大学信息工程学院，湖南 湘潭 411105)

一种MH/Ni动力电池模型及其SOC预测方法

刘国繁1，骆 晶2

(1.湖南工程学院电气信息学院，湖南 湘潭 411104；2.湘潭大学信息工程学院，湖南 湘潭 411105)

在传统的MH/Ni动力电池等效电路模型基础上，提出了一种改进的电池模型，将电池工作状态分为放电、放电停歇、充电、充电停歇4个不同阶段；设计了脉冲充放电实验，给出了参数辨识方法；利用此模型，提出了一种基于卡尔曼滤波的SOC估算算法。实验仿真结果表明，模型预测数据接近实测数据，所提出的电池模型及SOC估算方法精度较高。

MH/Ni电池；电池模型；卡尔曼滤波；荷电状态（SOC）

近年来，混合动力汽车（HEV）因节能环保的优点受到人们的重视，得到了广泛的研究。电池管理系统是混合动力汽车中的一个关键部件，准确估计电池的荷电状态（state of charge，简称SOC）是电动汽车蓄电池管理系统中最基本也是最首要的任务。但MH/Ni动力电池的SOC不可以直接测量，要准确估算SOC，必须建立良好的电池模型，通过电池的端电压、端电流等参数来估算SOC[1]。因此，建立准确的模型及采用精确的估算算法是提高SOC估算精度的重要途径，在电池管理系统的研究设计中具有重要的意义。

目前，电动汽车电池模型种类很多，本文在考察现有的传统电池等效模型的基础上，提出一种改进的电池模型，在此基础上进一步展开研究，利用适合于工程应用的卡尔曼滤波算法对其进行SOC预测，为电池SOC的估计提出了一种新的、有效的方法。

1 MH/Ni电池等效电路模型

电池工作时，内部的电化学反应是一个复杂的非线性过程，剩余容量受到电池电压、电流、温度、内阻、自放电、老化、循环次数等多种因素的影响。本文将电池的这个非线性过程作一个线性化处理，以传统的等效电路模型为研究基础[2-5]，提出了一种改进的MH/Ni电池等效电路模型,同时针对电池充放电的4种工作状态进行电路分析及参数辨识，为利用卡尔曼滤波算法对电池进行精确的SOC估算提供了基础。

1.1 MH/Ni电池的特性

图1、图2分别为常温下由10个1.2 V/(6 Ah)QNFT6-3型单体电池串联而成的单元电池SOC与开路电压之间的关系，以1C恒流充放电到相应SOC点，静置2 h后所得到的开路电压。可以看到，在实验室进行恒流充放电实验时，充放电电流相对稳定或变化平缓，可以用较为简单的静态模型来表示。但是在实际车载行驶条件下，电流的变化是剧烈且无规则的，温度等环境因素的变化也大，就需要用相对复杂的动态模型来描述电池的特性。

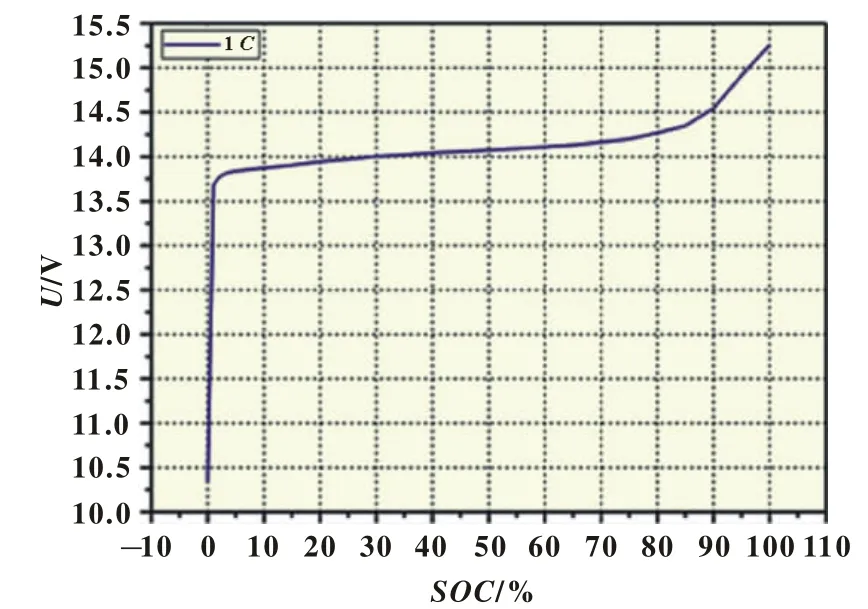
图1 常温下以1 C恒流充电MH/Ni蓄电池SOC与开路电压的特性曲线

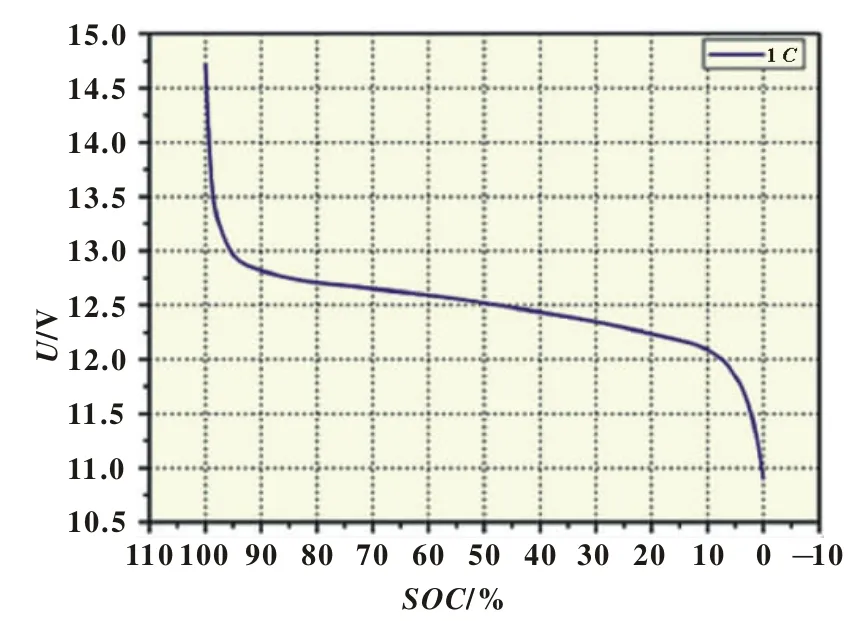
图2 常温下以1 C恒流放电MH/Ni蓄电池SOC与开路电压的特性曲线

从图1、图2可知，在充放电初始和结束阶段，电压值有一个比较大的升降幅度，开路电压变化剧烈，表示电池显示出一定的阻性，之后曲线又逐渐开始趋于平缓，表示电池略显现电容的特点；在20%≤SOC≤80%时，电池的开路电压变化较为平稳，为其主要的工作段，即充放电平台期。文献[6]提出，在放电初期和后期，电池的极化电压变化剧烈；在充电初始阶段和后期接近满电荷状态时，极化作用也相当明显。从而可知，开路电压首尾急剧变化主要应该是极化电压变化剧烈引起，考虑到这点，为模型的改进提供了基础。

1.2 改进的MH/Ni电池二阶等效电路模型

电池处于充放电状态时，会在外特性上表现为一些电阻电容的特性。根据这些特性，我们可以用电阻、电容、恒压源等电路元件组成的等效电路模型来模拟电池的动态。

Thevenin模型是一种使用广泛的典型电池等效电路分析模型，利用电阻电容RC环节来模拟电池在充放电过程中的内部复杂的反应。如图3所示，模型中E0是电池电动势，与电池SOC相关，I为负载电流，R是电池的欧姆内阻，描述电池阻性特性，R0是电池的极化内阻，与电容C并联构成容阻回路，用于模拟电池极化过程中表现出的动态特性。但Thevenin模型的主要缺点是，各个参数都被设为常量，而实际上这些量都是电池状态的函数，都与温度、电压、SOC等有关。

鉴于以上的考虑，在Thevenin模型的基础上进行研究，提出了一个改进了的电池等效模型，考虑电池充放电时元件值随电流和电压的变化。模型包含四种工作状态：充电、充电之后静置状态、放电、放电之后静置状态。在静置状态，电池既不接受电流，也不放出电流。在每一种工作状况下，可以通过指数关系式计算得到电池的端电压[7-8]。

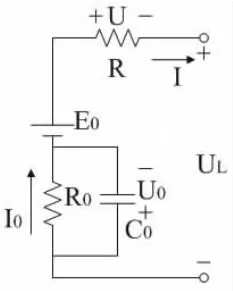
图3 Theven i n电池模型

图4是改进的MH/Ni蓄电池模型图。该模型包括了一个理想直流电压源Uoc(其值为开路电压)、电池的欧姆内阻R9和极化内阻R1～R8，以及与极化内阻并联的电容C1～C4。二极管D1、D2控制电池的充放电等四种状态，电池在放电和充电时，考虑到模型负载平衡和较好地反映电池的动态特性，每种状态下使用了两个R-C并联的组合。在电池模型处于放电状态即电流i(t)＜0时使用C1，R1和C2，R2，在电池放电后，处于静置状态时使用元件C1，R3和C2，R4。在放电状态下，二极管D1通，二极管D2断。同理，在电池模型处于充电状态即电流i(t)＞0时使用C3，R5和C4，R6。在电池处于充电后的静置状态时使用C3，R7和C4，R8。在充电状态下，二极管D2通，二极管D1断。

1.3 模型参数的获取

根据图4所示的模型，以放电为例进行分析，在t=0时刻，开关闭合，电池进入放电状态，通过外接负载Re放电，此时可得到下列拉普拉斯频域算式：

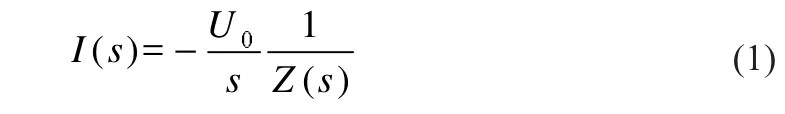
由拉普拉斯逆变换，可以得到i(t)的表达式：

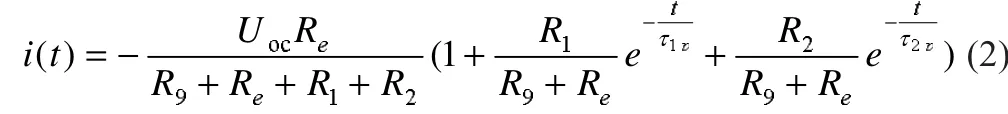
τ1p和τ2p是平衡时间常数，其中的电阻值为动态电路分析中假设电容短路时得到的戴维南等效电阻。

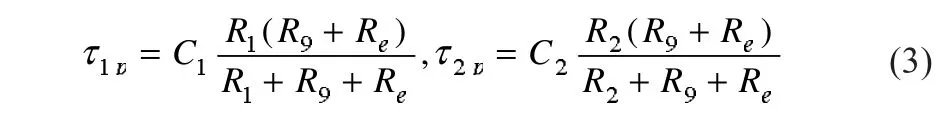
为了完成电池动态模型参数识别，需要完成不同充放电倍率下的实验。实验时，电池外接负载为0～4Ω，外接充电电压为15 V。通过调整负载大小，得到不同倍率下的电流与电压随时间变化的趋势。通过开关控制电池四种状态变化，分别为充电、充电停歇、放电、放电停歇四个阶段。

通过脉冲充放电等实验，便可以对模型进行参数辨识，运用Excel软件的多元线性回归分析功能计算得到电池模型参数，同时得到对应的回归判定系数[9]。对电池进行充放电，可由电压变化曲线大致确定τ的范围；在运用多元线性回归时，根据判定系数R2来确定τ的最佳值，R2越接近1，τ值越好。

通过完成全部SOC点复合脉冲实验后，使用多元线性回归方法分别对不同SOC点的复合脉冲实验数据进行处理，每个SOC点对应一组模型参数，以多元线性回归拟合原理和电路关系式为基础，利用Excel中的LINEST函数分析对应各个SOC点的电池模型参数，利用曲线拟合的方法，使用三次多项式拟合，从中提取出电池模型中“欧姆内阻-SOC”和充放电的时“开路电压-SOC”的数学关系，如下式所示：

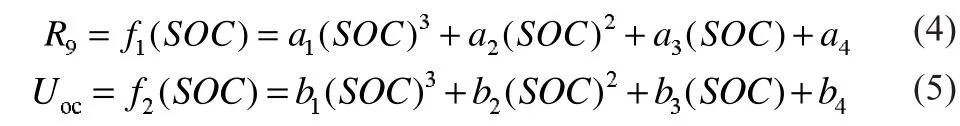
式中：α1、α2、α3、α4，b1、b2、b3、b4均为由模型参数得到的拟合系数，其中式（5）中的拟合系数分充放电两种情况，根据不同的工作状态选择相应的参数。

得到电池四种工作状态的电池参数后，根据电池的实际工作状态，选择充电、充电后暂态、放电、放电后暂态各状态的元件参数，通过卡尔曼滤波算法对电池SOC进行估算。

2 基于卡尔曼滤波算法的MH/Ni电池SOC估计

2.1 电池模型的数学描述方程

用安时计量法估计电池SOC的微分形式如下：

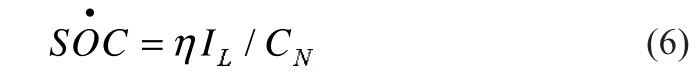
式中：η为电池的库仑效率。

由图4的电池模型电路结构，基于电路原理，将模型中的变量及参数之间的数学关系用状态空间模型来表示，以放电为例进行分析（其他三种状态分析方法相同），得到连续形式的电池状态空间模型如式（7）所示，负载电压UL与电路中元件电压间的关系如式（8）所示：

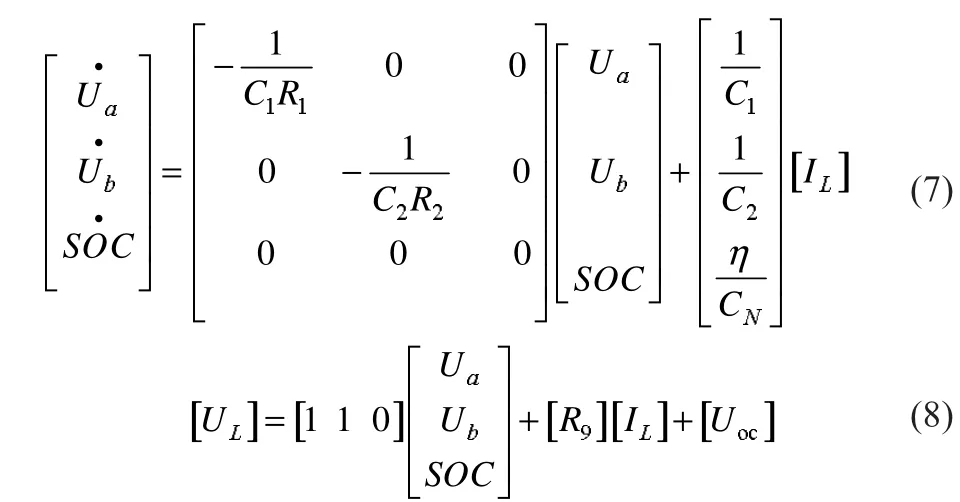
对式（7）、（8）进行离散化，得到离散后的状态空间模型如式（9）所示，其中Ts表示离散数据点IL,k和UL,k的时间间隔，对应于电池管理系统的采样时间。

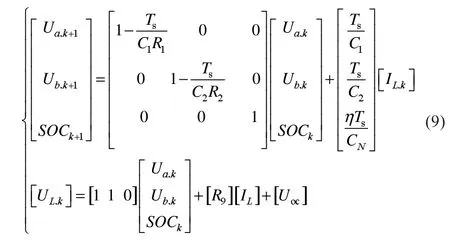
2.2 卡尔曼滤波法估计SOC

根据MH/Ni电池的数学描述式（9），可得到式（9）中相应的系统的状态矩阵Xk、系统矩阵、控制输入矩阵和

∧观测矩阵 C如下所示：

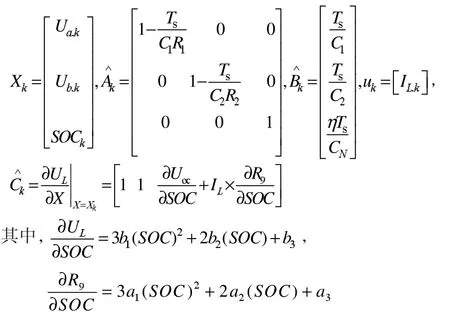
根据卡尔曼最优滤波理论[10-11]，建立电池SOC的卡尔曼滤波估算方程，其递推过程可归纳如下式：

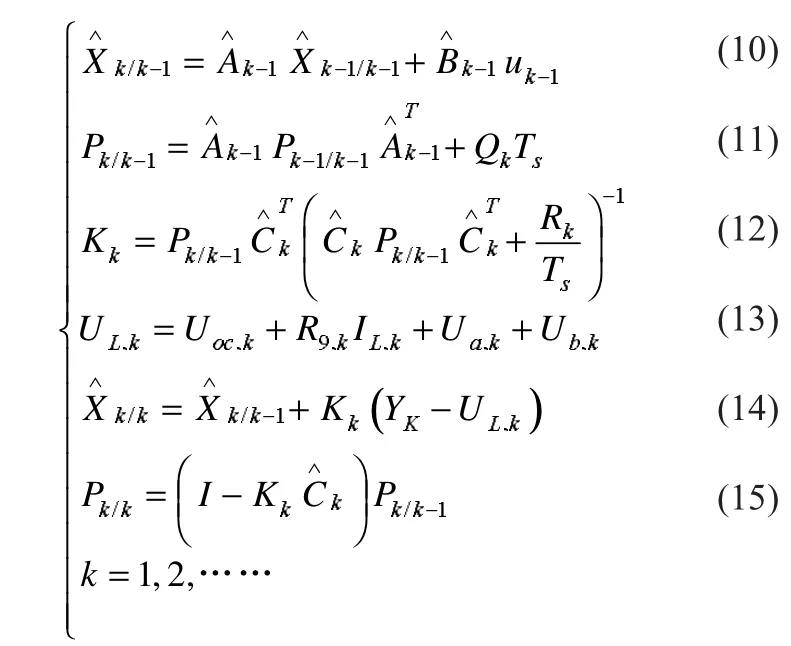
根据R-C支路中极化电阻和极化电流的值，式中极化电压Ua,k、Ub,k的计算如下：

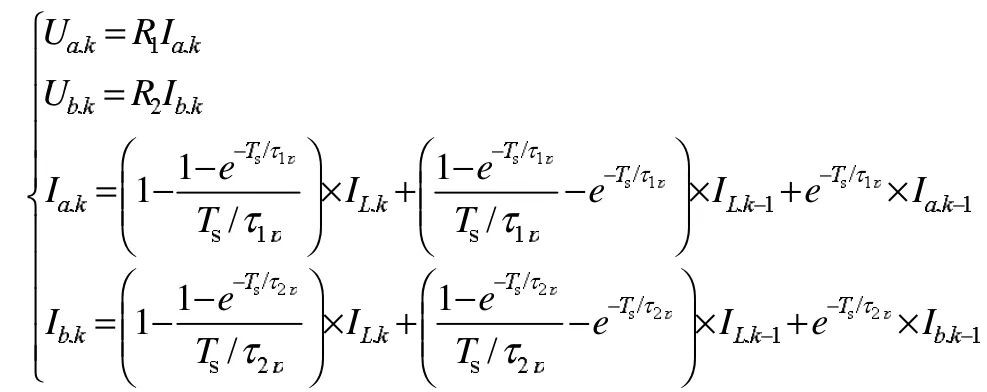
式中：YK为电池管理系统测量的MH/Ni动力电池组电压；UL,k为改进电池模型计算的MH/Ni动力电池组电压；Pk/k－1为预测值均方差；为系统状态预测值；Kk为滤波增益矩阵；为状态估计值；的第三个分量即为SOC的估计值；Pk/k为估计值均方差；Qk、Rk为噪声方差矩阵。

3 电池实验及结果分析

3.1 实验方案

在常温下，采取对电池进行脉冲充电及脉冲放电，并由此得到实验结果曲线，分别如图5和图6所示。图5为MH/Ni电池3 A脉冲充电曲线，图6为MH/Ni电池3 A脉冲放电曲线。实验分别是在氢镍电池放完电(SOC=0)和充满电(SOC=1)的状态下，分别进行3 A脉冲充电和放电，每次充电或放电1 Ah，即对应SOC增加或减少10%，然后停歇40分钟，共10次。

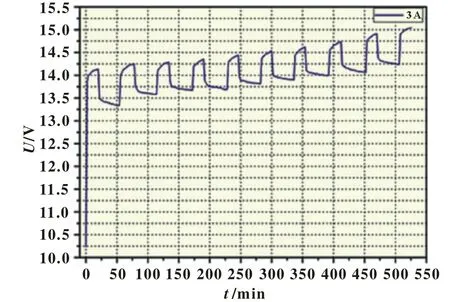
图5 氢镍电池0.5 C脉冲充电曲线

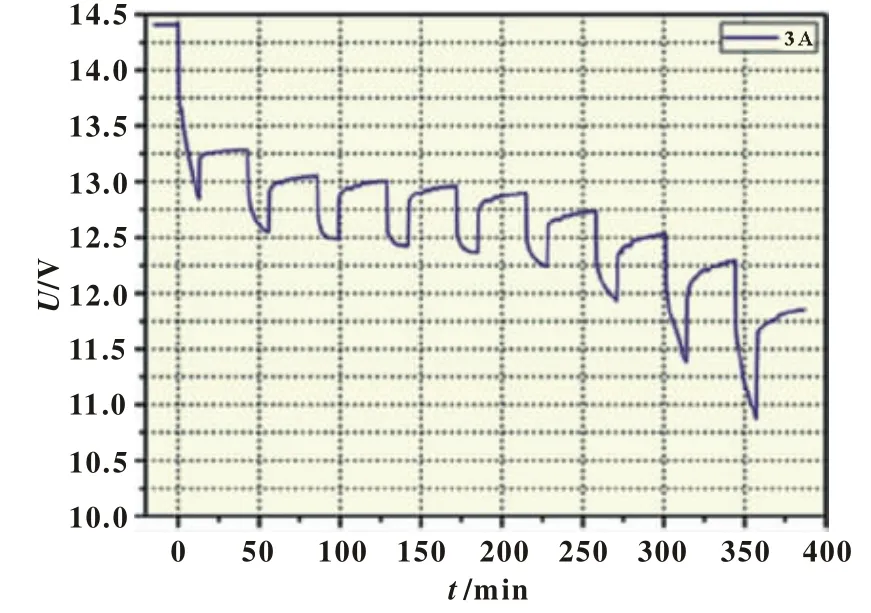
图6 氢镍电池0.5 C脉冲放电曲线

通过恒流充放电及脉冲充放电实验测量得到的电流和电压实验数据，对应每个SOC点，计算模型中各个参数的值，共得到10组参数，取其平均值作为最终电池模型参数确定电池模型。在放电状态下，通过负载电阻计算得到一些放电数据，如表1所示。

表1 放电及放电静置状态下一些实验参数

3.2 模型仿真验证

在对估算方法进行仿真验证之前，我们先来验证一下改进模型用于MH-Ni电池时的有效性和准确性。图7显示了利用改进电池模型估计得到的电池端电压与电池实测端电压的比较情况。图8显示了脉冲充电条件下，模型估计端电压的误差。

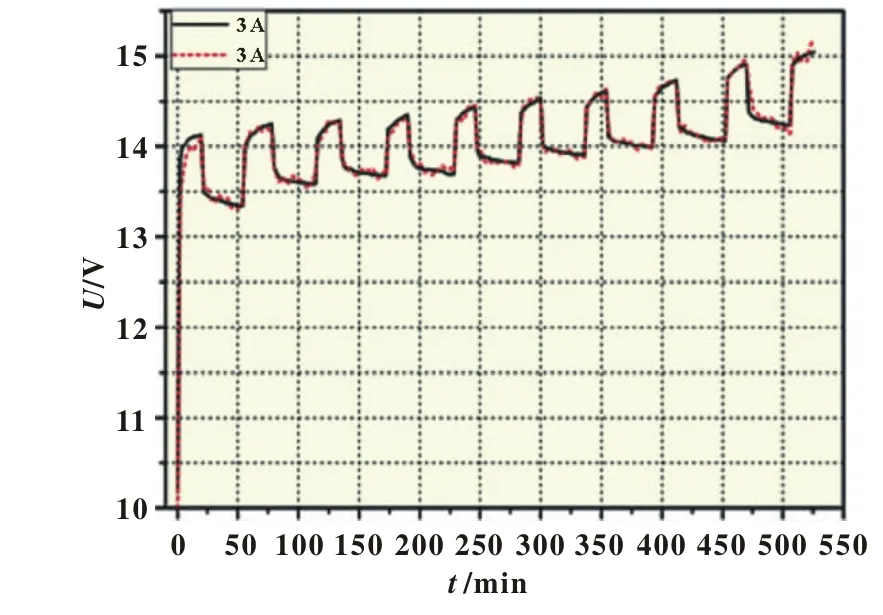
图7 实验与模型计算脉冲充电电压曲线对比

从以上两个图可以看到，利用此模型估计出的电池端电压对电池实测工作电压的跟随效果好，精度高。尤其是在SOC为20%～80%的范围内，实验曲线与模型估计方法得到的仿真曲线吻合得很好，在充电起始阶段和充电快结束时，模拟曲线与测量曲线有一定误差，整个过程电压误差控制在3%以内，模型精度较高。

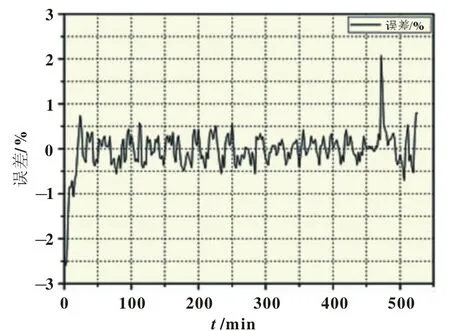
图8 模型计算数据在脉冲充电条件下的误差

3.3 估算方法仿真结果

根据实验数据，电池模型得到确定后，采用所提出的基于改进模型的卡尔曼估算方法对电池SOC进行预测估算，通过MATLAB仿真实验得出结果分析，以验证算法的准确性。

以放电为例，根据已辨识得到的相应电池模型各个参数及测量值带入式（10）～（15）中，进行计算及生成曲线，最终得到基于改进模型的SOC计算结果。电池初始SOC为90%，以某一放电倍率对电池进行放电，终止SOC为16%，电池SOC的估计值和通过实验得到的测量值结果比较如图9。

可以看到，在改进模型的基础上利用卡尔曼滤波算法得到的估算值较为准确，可以有效地跟踪电池SOC的变化，最大误差小于5%，整体仿真曲线拟合效果较好。这是因为卡尔曼滤波算法实际上是根据状态方程和输出观测方程的误差，利用实测电压与估计电压进行比较反馈，在计算过程中不断调整状态估计值。

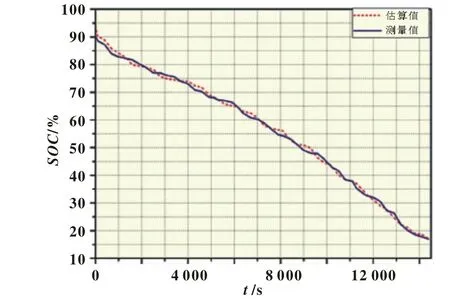
图9 充电时SO C估计值与实验测量值比较

4 结论

本研究根据混合动力车用氢镍电池的特点，对电池等效模型进行了改进，分充电、充电之后静置状态、放电、放电之后静置状态四种状态，使得模型更直观、物理意义更明确。并在此改进模型的基础上，利用一套卡尔曼滤波算法来进行电池SOC的预测，电池模型越精确，算法估计的SOC越准确。实验和仿真结果表明，将卡尔曼滤波算法应用到所改进的电池模型是合理的。

本文的模型只考虑了常温下电池的特性，具体应用时还需要计入温度的变化对电池参数的影响。同时，本文未考虑电池老化对电池参数的影响，可在对电池做进一步老化实验的基础上，分析出老化因子，根据电池的循环次数来修正各个参数。总体来说，本算法很容易应用于电池管理系统中，在工程上容易实现。

[1] 李超，商安娜.电动汽车用氢镍电池二阶RC模型的研究[J].电源技术，2011,35（2）：195-197.

[2] GEUERW.Investigation about the aging behavior of lead battery [D].Aachen:RWTH,1992.

[3]SCHWEIGHOFER B,RAAB K M,BRASSEUR G.Modeling of high power automotive batteriesby the use of an automated test system[J].IEEE Transactions on Instrumentation and Measurement, 2003,52(4):1087-1091.

[4]CHIASSON J,VAIRAMOHAN B.Estimating the state of charge of a battery[J].IEEE Transactions on Control Systems Technology, 2005,13(3):465-470.

[5]JANTHARAM IN N,ZHANG L.A new dynam icmodel for lead-acid batteries[C]//IEEE Power Electronics,Machines and Drives.New York:IEEEPress,2008：86-90.

[6] 温家鹏，姜久春，文锋，等.Kalman算法在纯电动汽车SOC估算中的应用误差分析[J].汽车工程,2010，32(3):188-192.

[7]PROTOGEROPOULOSC,MARSHALL R H，BRINKWORTH B J. Battery state of voltage modeling and an algorithm describing dynamic conditions for long-term storage stimulation in a renewable system[J].Solar Energy,1994,53(6)：517-527.

[8] SIMJEE F,CHOU PH.Accurate battery lifetime estimation using high-frequency power profile emulation[C]//Proceedingsof 2005 international symposium on Low power electronics and design.San Diego,CA,United states:Institute of Electrical and Electronics Engineers Inc.,2005:307-310.

[9] 蔡志辉，刘国繁，骆晶.基于EXCEL的车用动力电池模型参数辨识研究[J].湖南工程学院学报,2010,20(4):2-4.

[10] 史宗科.最优估计的计算方法[M].北京：科学出版社,2001.

[11] 邓自立.卡尔曼滤波与维纳滤波[M].哈尔滨：哈尔滨工业大学出版社,2001.

Mathematicmodel forMH/Nibattery and SOC estimation based on Kalman filter

LIU Guo-fan1,LUO Jing2
(1.College of Electricaland Information Engineering,Hunan Institute of Engineering,Xiangtan Hunan 411104,China; 2.College of Information Engineering,XiangTan University,Xiangtan Hunan 411105,China)

An improved battery model for MH/Ni battery was presented on the base of classical equivalent circuit model.The battery work states were divided into four phases,namely,charge phase,charge idle phase,discharge phase,discharge idle phase.Pulse charge and discharge experiments were designed and identification method of parameters was introduced.Based on the improved model,an estimatedSOCalgorithm by using Kalman filtering was proposed.The experiment simulation results show that the predicted data match the measured data very well and the proposed model andSOCestimation have good precision.

MH/Ni battery;battery model;Kalman filter;state of charge(SOC)

T M 912

A

1002-087 X(2013)11-1985-04

2013-04-15

湖南省科技计划项目(2009GK3074)

刘国繁（1959—），男，湖南省人，教授，硕士生导师，主要研究方向为计算机测控技术、嵌入式系统应用。