电网电压不平衡下电压同步信号的检测

陈益广，闫志乾，王颖

（1.天津大学智能电网教育部重点实验室，天津 300072；2.天津经济技术开发区汉沽现代产业区总公司，天津 300480）

电网电压不平衡下电压同步信号的检测

陈益广1，闫志乾1，王颖2

（1.天津大学智能电网教育部重点实验室，天津 300072；2.天津经济技术开发区汉沽现代产业区总公司，天津 300480）

在对传统锁相环进行充分研究的基础上，通过在两相静止坐标系中利用状态空间估计和一系列数学变换，重新建立电网电压的动态模型，以此获得电网三相电压基波成份的估计值，再利用改进的T/4延迟法分离得到基波电压正负序分量。最后，结合传统锁相环技术实现对基波电压相角的准确跟踪检测。仿真分析表明，该方法既能快速准确的分离出电网电压中正、负序基波分量，又能准确跟踪电网电压的相角，同时可得到电网电压的频率和幅值。

状态空间估计；锁相环；正负序分量；谐波

近年来随着分布式发电尤其是风力发电的快速发展，风力机组对于电力系统的稳定运行产生着越来越重要的影响。为了增强风电机组的可靠运行，必须对电网电压不平衡下电压的相角、幅值进行快速准确的跟踪检测。目前锁相环PLL（phase locked loop）技术已广泛应用于对电网电压的信号检测，在正常电网条件下，PLL能够快速准确跟踪电网电压的相角。然而当电网电压发生故障时，传统锁相环并不能准确跟踪电网电压的相角[1～4]。

对于电网电压谐波分量、负序分量的检测，目前常用基于瞬时无功功率的方法，但该方法以基波正序电压作为参考，只能检测电流中的谐波，不能检测电压中的谐波，且不能把谐波和基波负序分量相分离[5]。针对电网电压不平衡及含有谐波的情况，文献[6，7]提出了增强型锁相环EPLL（enhanced phase locked loop），通过改进鉴相器的机制，可以获得更多的电网电压信息，如幅值、相角等。但是，EPLL暂态响应慢，且主要适用于单相电压信号的检测情况。文献[8，9]分别提出了一种在PLL前加闭环重复控制器和低通滤波器来滤除电网电压谐波的方法，但这类方法会导致响应速度变慢，且并不能检测出电网电压的正负序分量。文献[10，11]提出了利用自适应滤波器ANF（adaptive notch filter）来滤除电网电压中谐波的方法，该方法能很好地去除电网电压中的谐波，但是算法复杂，通常只应用于单相系统，应用于三相系统时，要对每一相都加自适应滤波器，不易实现。文献[12]提出了一种状态空间估计器，在电网电压不对称或含有谐波时对电压同步信号都有很好的动态响应，但是该方法并未考虑到电压的补偿量，且对于电网电压角频率涉及了开方运算，实际中并不容易实现。

本文所提出的新方法，利用Clarke变换将三相电压矢量转换到αβ两相静止坐标系中，在αβ两相静止坐标系中，通过对电压求导重新构建电网电压的矢量模型；在新构建的模型上，利用状态空间估计法获得电网电压矢量的估计值；在此基础上，通过改进的T/4延迟法对电网电压进行正负序分离；并结合传统锁相环技术，实现对电网电压的正负序分量幅值和相角进行检测。

1 电压不平衡时基波电压估计值的确定

1.1 电网电压的动态模型

三相三线制系统中，由于没有中性点接线，电网的三相相电压并不能直接测得。因此，只能通过测量三相线电压来间接获得三相相电压信号。相电压与线电压之间的关系为

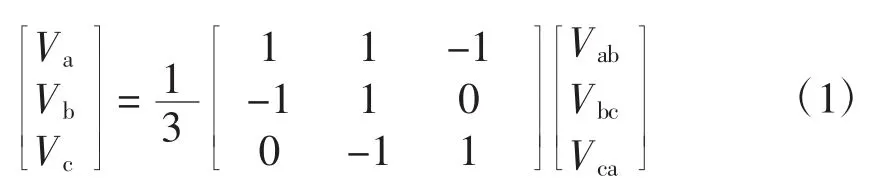
由于在三相三线制系统中不存在零序分量，同时计及电网电压谐波时，三相相电压可表示为

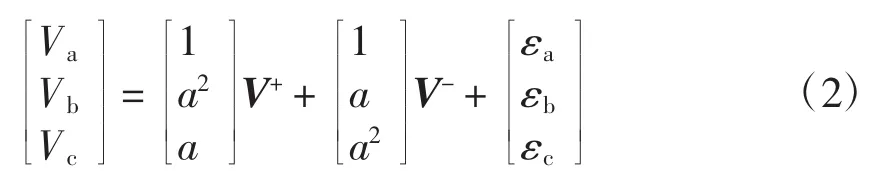
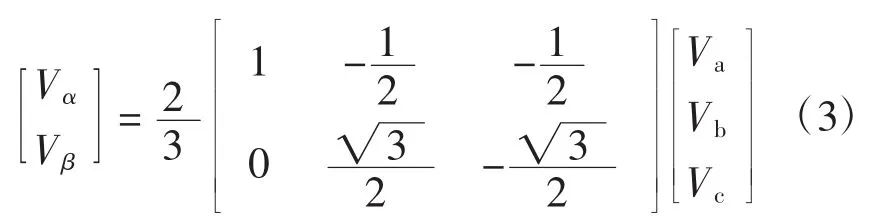
考虑到电网电压信号主要是由基波成分组成，在αβ两相静止坐标系中，Vαβ=[VαVβ]T可表示为

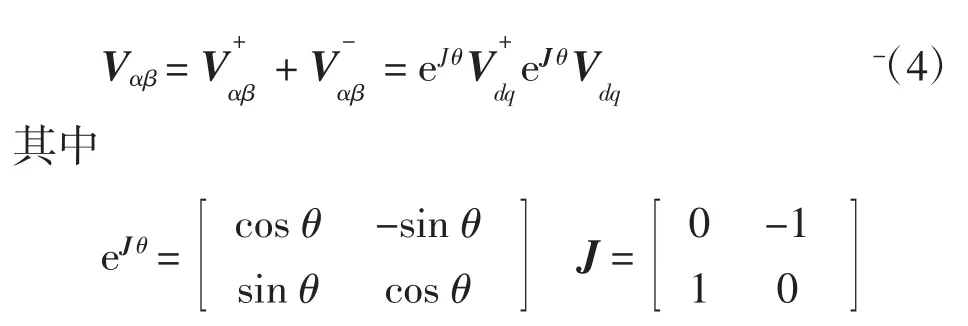
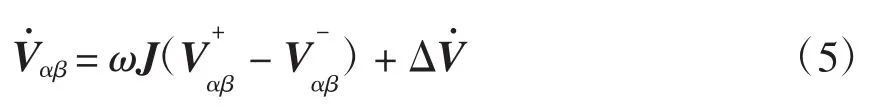
为了建立电网电压的动态模型方程以及运算方便，令

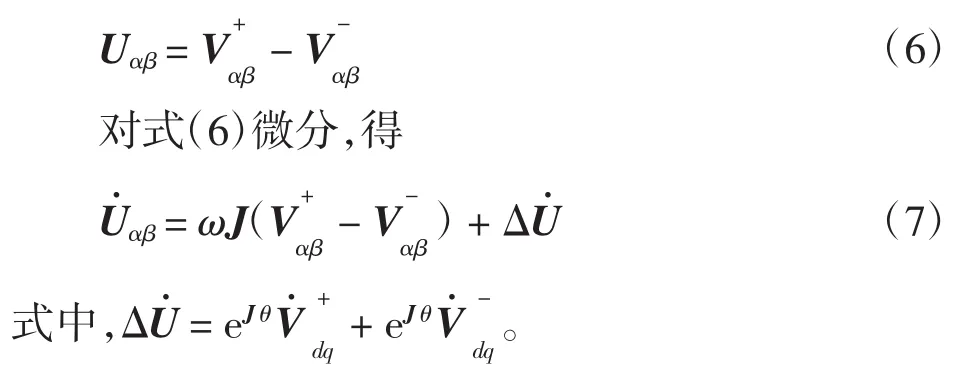
进一步简化式（5）和式（7），可令Rαβ、分别为

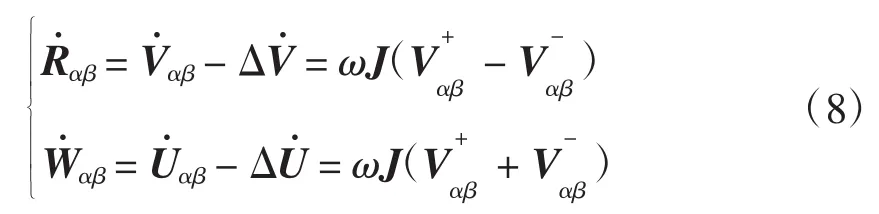
由式（8）可以看出，两式中都含有参数ω。为了便于设计、分析，以及减小参数的误差，利用基波电压的理论角频率与参数ω可以构造为

对式（9）求微分，可得

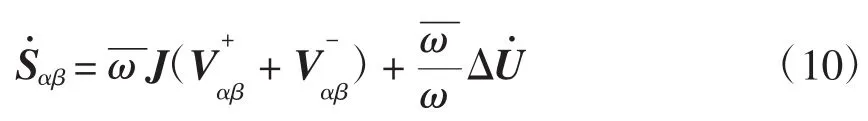
同理简化式（10），可得

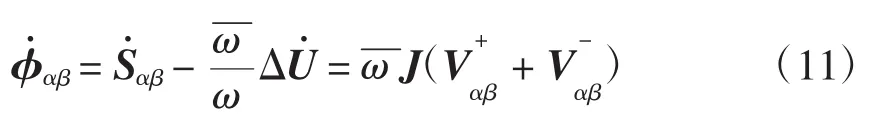
联立式（5）、式（8）以及式（11），可得到关于电网电压的动态模型为

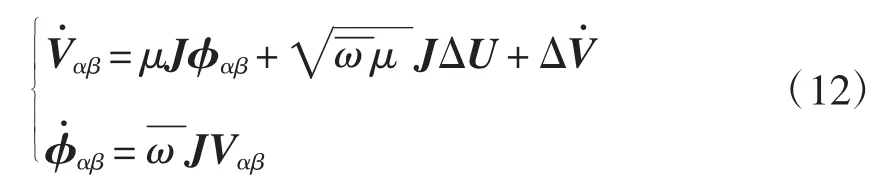
1.2 电网电压估计值的确定

式中，λ是一个用来引出相应阻尼的正参数。未知参数μ^的确定遵循用于判定系统稳定性的李亚普诺夫第二方法。联立式（12）和式（13）得

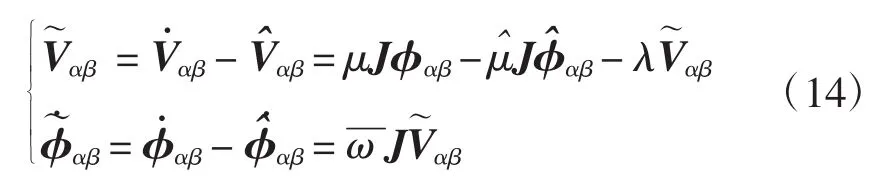
式（14）为状态调节器的误差值，由此可获得状态调节器的最优性能指标二次型函数为

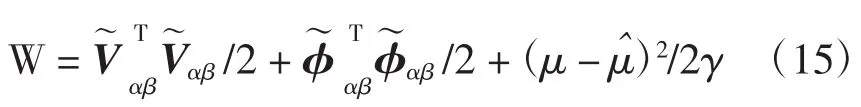
依据李亚普诺夫第二法对动态系统稳定性的判别，式（15）所示二次型函数必须达到正定，且其导数为负半定，则μ^需满足

根据式（13），并结合式（5）与式（16），考虑补偿量，便可设计出关于三相电网电压在两相静止坐标系中电压估计值αβ的自适应估计器。

1.3 电网电压的正负序分离和相角检测

对于电网电压正、负序分量的分离，传统方法采用T/4延迟法，其中T为电网电压周期，即对电网电压延迟1/4电网电压周期。利用T/4延迟法，电网电压估计值的正负序分量可表示为

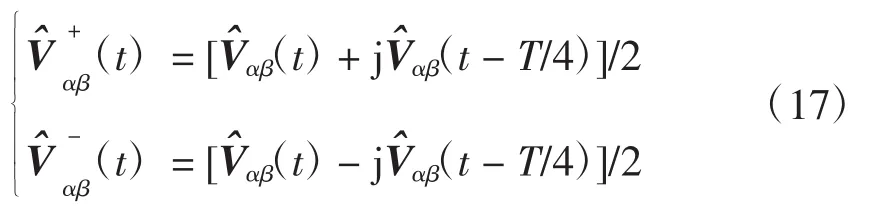
由式（17）可知，该方法存在T/4的固有延迟。对于随时间按正弦规律变化的电压，对电压信号进行T/4延迟，就等同于对电压求微分。如果假设电网电压频率基本维持恒定，就可以利用求微分的方法对T/4延迟法进行改进。取微分后，需添加一个-1/ω模块来补偿电压取微分时产生的-ω。设采样时间为TS，为了使αβ（t）与求微分后的信号保持同步，需对αβ（t）同时延迟相同的采样时间TS，而TS≪T/4。

在电网电压正负序分离的基础上，结合传统锁相环技术，即可对电网电压的相角进行检测。传统锁相环应用于三相电网电压相角检测时，先将三相电压相量变换为同步旋转电压相量Vd、Vq，以=0为参考值，反馈值与其比较产生的误差值经PI调节后得误差角频率，误差角频率与理论角频率相加后，再经积分环节便可锁定电网电压相角，同时也可获得电网电压的幅值和频率。

综合以上分析，可得到如图1所示的改进锁相环的检测原理框图。图中，Kp和TPLL分别为比例系数和积分时间常数。

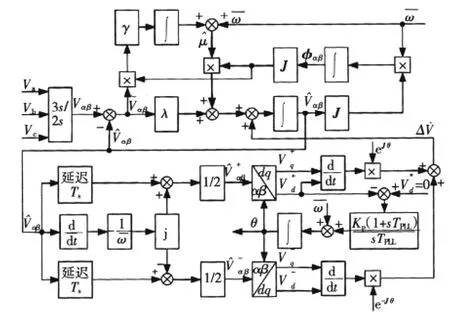
图1 改进锁相环检测的原理框图Fig.1Principle block for detecting of improved PLL

3 仿真分析

为了验证改进锁相环在电网电压不平衡或含有谐波时对电压同步信号的检测效果，本文利用Matlab/Simulink仿真软件对锁相环的动态响应进行了仿真研究。仿真中对于参数λ和γ值的确定，最有效的途径为通过反复试验找到合适的λ、γ值使系统达到最优调节，一般可取λ=300、γ=2。

图2为电网电压频率波动时两种锁相环的动态响应。图2（a）为在t=0.14～0.24 s内，频率由50.0 Hz线性变化至50.2 Hz时的三相电网电压。仿真表明，传统锁相环和改进锁相环都可准确检测频率变化。且传统锁相环由于未考虑谐波、不对称等因素，在单纯频率快速变化时，其有一定的优势。

图3为电网电压不对称时传统锁相环和改进锁相环的动态响应的仿真结果。图3（a）为三相额定平衡电压突然在t=0.13 s时刻正序分量跌落50%、负序分量增加20%的不平衡电网电压。

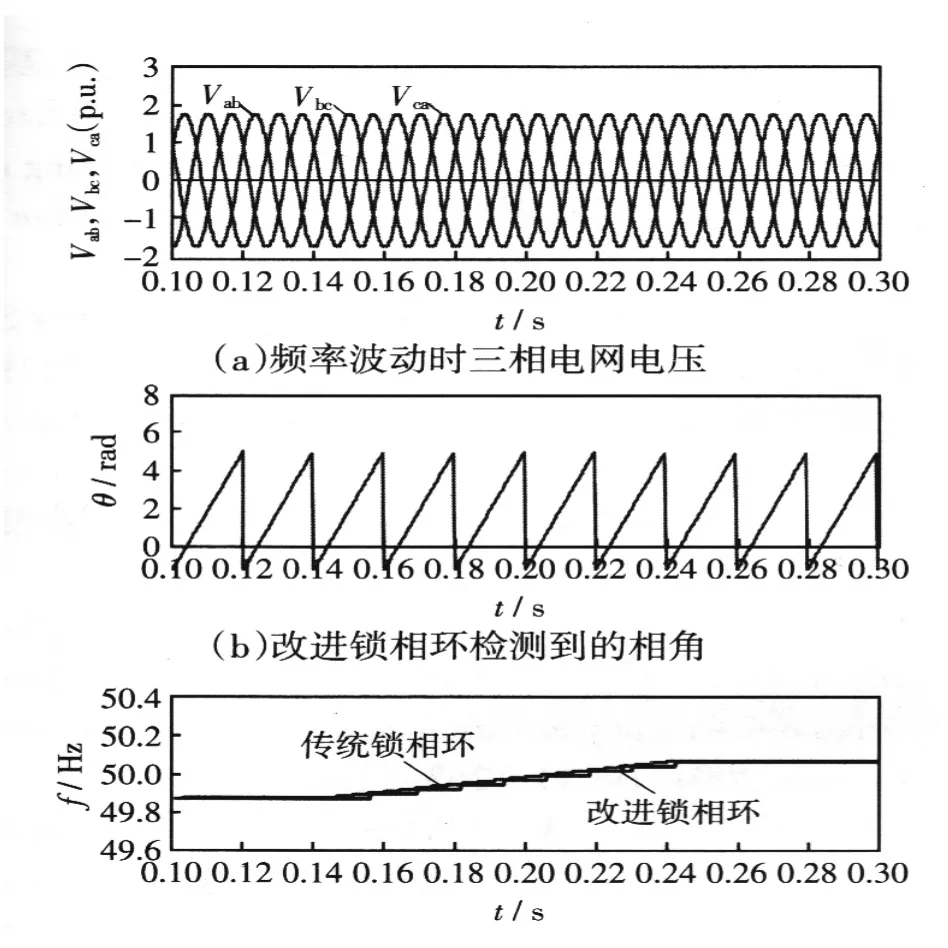
图2 电网电压频率波动时锁相环的动态响应Fig.2Dynamic response of the PLL under the condition of the grid voltage frequency fluctuation

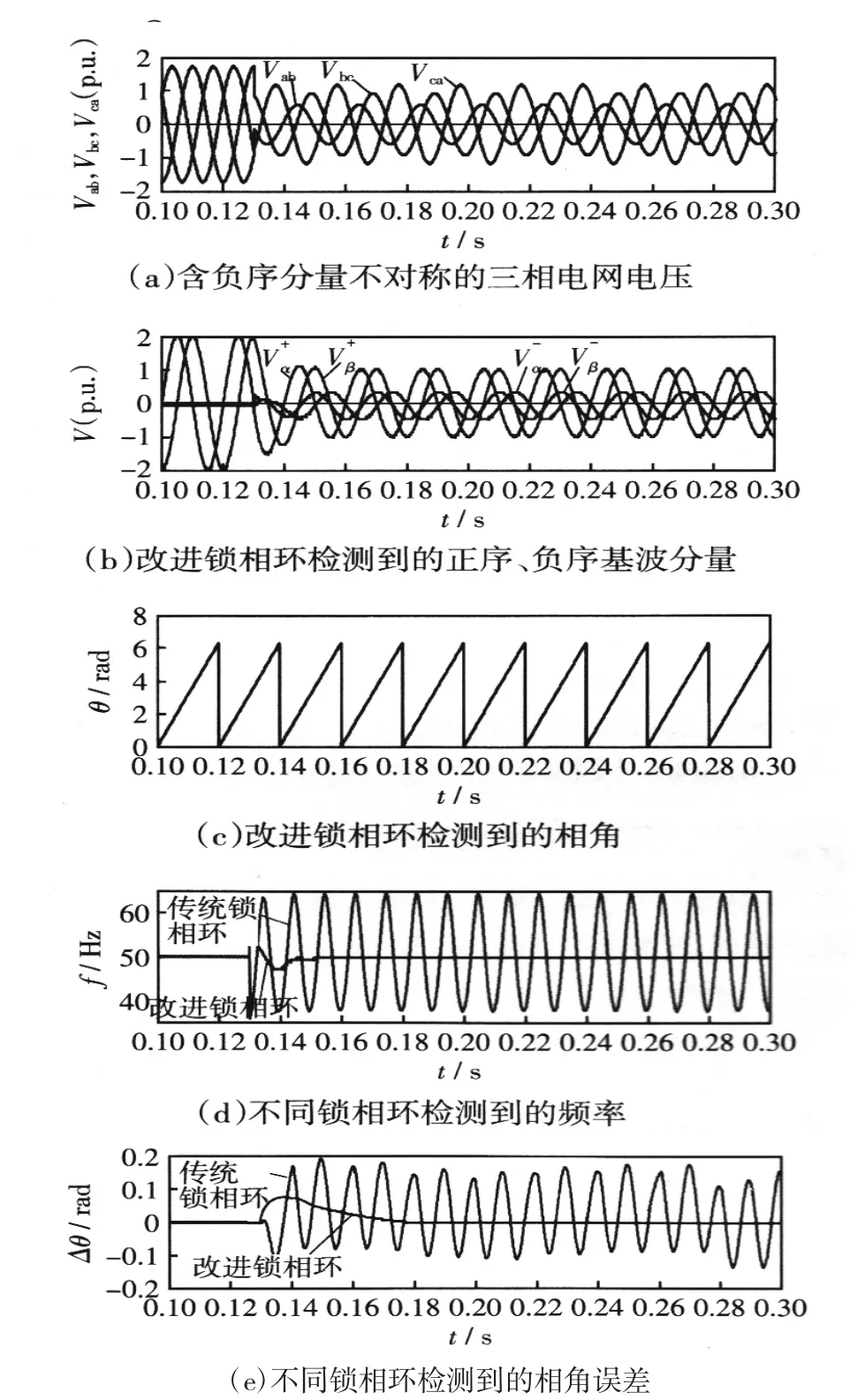
图3 电网电压不对称时锁相环的动态响应Fig.3Dynamic response of the PLL under the condition of the grid voltage unbalanced

由图3（b）可以看出，改进锁相环准确地分离出了电网电压的正负序分量；图3（c）表明改进锁相环能准确检测电网电压不平衡时的相角；由图3（d）和图3（e）可以看出传统锁相环在电网电压不平衡时，检测到的频率出现了15 Hz左右的上下波动，导致检测到的相角和真实相角之间存在很大误差，并不能实现对相角和频率的准确跟踪检测；而改进锁相环检测到的频率只在电压跌落瞬间出现短暂且很小的波动后便迅速恢复为50 Hz，检测到的相角与真实相角只在电压跌落瞬间存在很小的误差，从而能实现对相角和频率的准确跟踪检测。

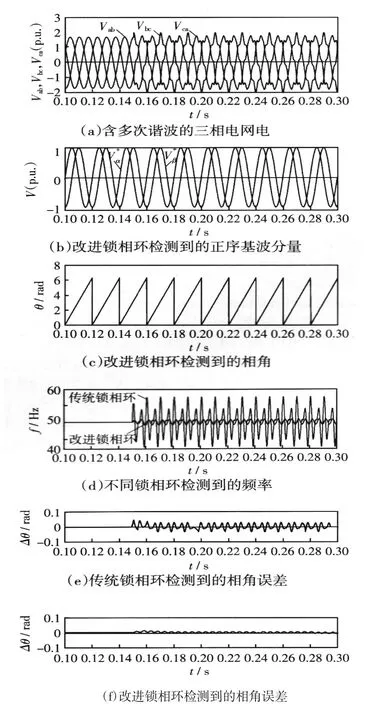
图4 电网电压含5次，7次谐波时锁相环的动态响应Fig.4Dynamic response of the PLL with 5 harmonics and 7 harmonics existing in the grid voltage

图4为在电网电压含有多次谐波时传统锁相环和改进锁相环的动态响应的仿真结果。图4（a）表示在t=0.15 s时刻电网电压中突然加入10%的5次谐波和7%的7次谐波的仿真结果。图4（b）为改进锁相环检测到的正序基波电压；图4（c）为改进锁相环检测到的电网电压相角。由图4（d）、4（e）可以看出，电网电压中含有多次谐波时，传统锁相环因未考虑谐波影响，检测到的频率会出现大约10 Hz的上下波动，检测到的相角与真实相角之间存在0.05 rad的误差，并不能准确跟踪电网电压相角；而图4（d）、4（f）表明，改进锁相环对谐波有很好的鲁棒性，能准确估计出电压基波分量，检测到的频率只有大约1 Hz的波动，检测到的相角与真实相角之间只存在极小误差，从而实现了对相角和频率的准确跟踪检测。

3 结论

（1）改进锁相环在电网电压不对称或频率变化时能准确的分离出电网电压正负序分量，并准确跟踪电网电压的相角。

（2）电网电压含有多次谐波时，改进锁相环有很好的鲁棒性，能够完全估计出电网电压的基波分量，并实现对电压相角和频率的准确跟踪检测。

[1]周鹏，贺益康（Zhou Peng，He Yikang）.电网电压不对称且谐波畸变时基波电压同步信号的检测（Synchronization signal detection of fundamental voltage under unbalanced and harmonic distorted grid voltage conditions）[J].仪器仪表学报（Chinese Journal of Scientific Instrument），2010，31（1）：78-84．

[2]刘义成，张学广，景卉，等（Liu Yicheng，Zhang Xueguang，Jing Hui，et al）.电网电压正负序分量快速检测算法（Fast detection algorithm of grid voltage positive and negative sequence components）[J].电工技术学报（Transactions of China Electrotechnical Society），2011，26（9）：217-222．

[3]周鹏，贺益康，胡家兵（Zhou Peng，He Yikang，Hu Jiabing）.电网不平衡状态下风电机组运行控制中电压同步信号的检测（Detection of voltage sychronization signals for a wind energy generation system unbalanced grid conditions）[J].电工技术学报（Transactions of China Electrotechnical Society），2008，23（5）：108-113．

[4]黄德旭，元学广（Huang Dexu，Yuan Xueguang）.基于dq运算方式的改进型谐波检测方法（Improved harmonic current detecting method based on d-q calculating mode）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2007，19（2）：103-107．

[5]袁旭峰，程时杰，文劲宇（Yuan Xuefeng，Cheng Shijie，Wen Jinyu）.改进瞬时对称分量法及其在正负序电量检测中的应用（An improved method of instantaneous symmetrical components and its detection for positive and negative sequence current）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（1）：52-58．

[6]Karimi-Ghartemani M，Iravani M R．A method for synchronization of power electronic converters in polluted and variable-frequency environments[J].IEEE Trans on Power Systems，2004，19（3）：1263-1270．

[7]Rodriguez P，Luna A，Ciobotaru M，et al.Advanced grid synchronization system for power converters under unbalanced and distorted operating conditions[C]//32nd Annual Conference on IEEE Industrial Electronics.Paris，France：2006．

[8]Timbus A V，Teodorescu T，Blaabjerg F，et al．PLL algorithm for power generation systems robust to grid voltage faults[C]//IEEE Power Electronics Specialists Conference. Jeju，South Korea：2006．

[9]Saitou M，Matsui N，Shimizu T.A control strategy of single-phase active filter using a novel d-q transformation[C] //IEEE Industry Applications Conference.Salt Lake City，USA：2003．

[10]Yazdani D，Mojiri M，Bakhshai A，et al.A fast and accurate synchronization technique for extraction of symmetrical components[J].IEEE Trans on Power Systems，2009，24（3）：674-684．

[11]Mojiri M，Bakhsha A R.An adaptive notch filter for frequency estimation of a periodic signal[J].IEEE Trans on Automatic Control，2004，49（2）：314-318．

[12]Escobar G，Martinez-Montejano M F，Valdez A A，et al. Fixed-reference-frame phase-locked loop for grid synchronization under unbalanced operation[J].IEEE Trans on Industrial Electronics，2011，58（5）：1943-1951．

Synchronization Signal Detection of Voltage under Unbalanced Grid Voltage Condition

CHEN Yi-guang1，YAN Zhi-qian1，WANG Ying2
（1.Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China；2.Corporation of TEDA Industrial Park，Tianjin 300480，China）

Based on the full study on the traditional phase-locked loop，the dynamic model of the grid voltage can be re-established and the estimation of the three-phase voltage fundamental components can be obtained by a series of transformations in two-phase stationary coordinate system.Positive and negative sequence components of the fundamental voltage can be separated by using the improved T/4 delay method.Then it can realize accurate tracking and detection of the voltage phase angle combined with the traditional phase locked loop technique.Simulation results verify that the method not only can quickly and accurately separate out positive and negative sequence of the grid voltage，but also can realize accurate tracking of the phase angle of the voltage and can get the frequency and amplitude of the voltage at the same time.

state space estimate；phase locked loop；positive and negative sequence component；harmonics

TM762

A

1003-8930（2013）03-0098-05

陈益广（1963—），男，博士，教授，博士生导师，研究方向为电机设计及其控制。Email：chenyiguang@tju.edu.cn

2012-11-16；

2013-01-05

闫志乾（1986—），男，硕士研究生，研究方向为电机设计及其控制。Email：yanziqian.hi@163.com

王颖（1980—），女，硕士，工程师，研究方向为电气工程。Email：wangying_1128@yahoo.cn