基于管道爆炸数值模拟的架空天然气管道并行间距研究

王德国

(中国石油大学机械与储运工程学院,北京 102249）

基于管道爆炸数值模拟的架空天然气管道并行间距研究

王德国

(中国石油大学机械与储运工程学院,北京 102249）

从天然气管道失效泄漏引发爆炸现象出发,通过理论分析建立架空管道泄露模型,应用Matlab计算出管道泄露总量中参与爆炸的体积,通过TNT当量法将体积值转化为管道爆炸模型的初始当量。利用Autodyn软件建立管道爆炸物理模型,计算不同并行间距下管道受并行管线爆炸冲击超压及变形量。依据管道椭圆应变准则评定不同并行间距下管道受冲击变形风险。结果表明：架空管线受并行天然气管线爆炸冲击产生的变形破坏为超压破坏和冲量破坏两种形式。架空管道大变形位置为正对爆炸源最近点和背对爆炸源最远点。架空天然气管道安全并行间距：一级和二级风险距离分别为0～2和2～5 m,三级风险距离为5 m以上。将数值模拟结果与理论计算结果对比,验证了该数值计算方法的可行性。

并行管道;TNT当量法;管道爆炸;并行间距

影响管线并行敷设间距的因素包括：管道失效、热传导效应、带压封堵空间、管道施工与维护[1-2]。对并行间距起决定作用的为管道破裂失效因素,其主要作用形式为：管线泄漏气体受明火引燃发生爆炸对管线产生冲击破坏[3]。目前的国外设计规范仅从管道腐蚀、同沟敷设、交叉敷设、施工间距和阴极保护等方面规范并行管线敷设间距,并未考虑管道失效泄漏对并行管线的破坏影响。由中国石油天然气股份有限公司天然气与管道分公司编制的《油气管道并行敷设设计规定》[4]在国内管道工程建设标准基础上,加入管道失效、热传导效应等影响因素。但该规定只适用于明管敷设并行管线,未考虑架空管线和埋地管线这两种敷设状况,且其失效模型为弹坑模型,与实际爆炸模型存在一定差别[5-6]。笔者采用Autodyn软件对管道泄漏爆炸模型进行数值模拟计算,定量分析不同并行敷设间距下天然气管道受爆炸冲击所产生的变形与失效,确定地上天然气并行管线敷设的安全间距。

1 泄漏扩散模型及TNT当量计算

1.1 管道泄漏模型

天然气管道泄漏分为孔口泄漏和裂缝泄漏两种[7],并以孔口泄漏为主。孔口泄漏可看作可压缩气体孔口流出过程,基本模型为圆孔口泄漏。天然气按理想气体考虑,小孔(孔口）泄漏过程视为绝热过程,结合伯努利方程和绝热方程可得出泄漏速度为

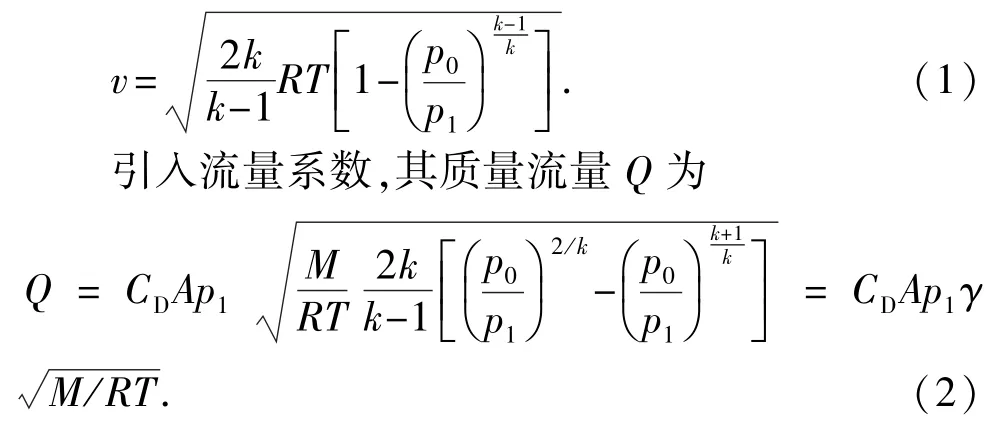
实际泄漏过程中必须考虑局部摩擦阻力损失,因此添加孔口流速系数φ对理论计算值进行修正。则式(1）和式(2）修正为

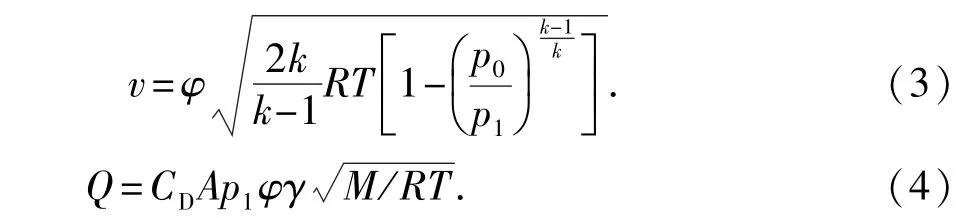
式中,φ为流速系数,表示实际流速与理论流速之比,由于实际泄漏速度小于理论计算值,一般取0.97～0. 98;k为绝热指数,天然气取k=1.3,R= 8.314 J/(mol·K）为气体常数;p1为气体泄漏前压力;A为泄漏孔面积;M为气体分子量,天然气取0.016 kg/mol;CD为流量系数,在这里遵循最危险原则,取CD=1. 0;γ为泄漏速度系数。

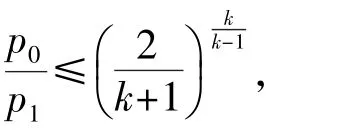
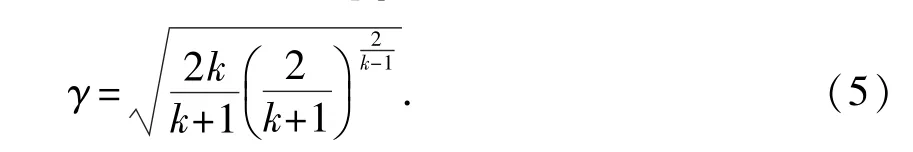
1.2 气体扩散模型

可燃气云发生气相爆轰的比率不高于总体积的5%,且天然气的爆炸下限浓度为5.3%,要计算输气管道泄漏产生的爆炸总冲量,首先须确认泄漏扩散浓度大于5.3%的天然气分布情况。

常用气体扩散模型包括高斯模型、BM模型[8]、Sutton模型和FEM3模型[9]等,考虑到输气管道泄漏状况,采用高斯烟羽模型进行分析。

高斯烟羽模型的浓度分布为

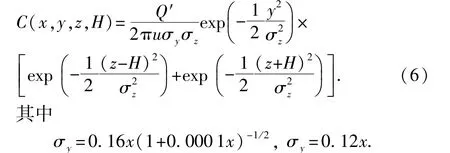
式中,C为下风方向x、横向y、距地面高度z处的泄漏气体浓度;H为泄漏源有效高度;u为源高H处的平均风速;Q′为源的体积流量,m3/s;σy、σz分别为水平、垂直方向扩散系数。

1.3 Matlab模拟泄漏扩散过程

联立式(4）和式(6）并进行对数化转换,管道气体泄漏扩散模型为

泄漏量Q′的表达式由式(4）确定。

结合陕京二线输气管道运行参数,取CD=1,p1=6 MPa,φ=0.98。泄漏孔一般为长条状,长度为管道内径的20%～100%,这里取50%,陕京二线主管线均采用X80管线钢材料,外直径1 219 mm,内直径1175 mm,取泄漏孔面积A=6 mm2,整理简化得：

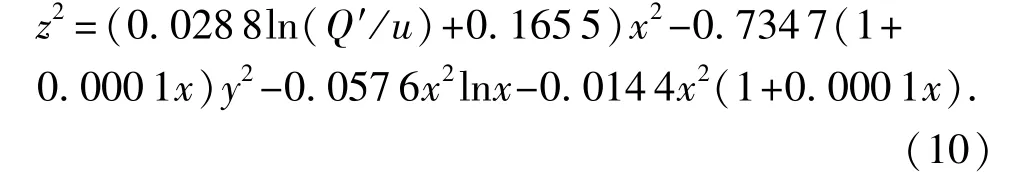
取风速u=2 m/s,Q′=8.312 5 m3/s,泄漏方向为水平x轴方向,经拟合后的泄漏模型见图1。

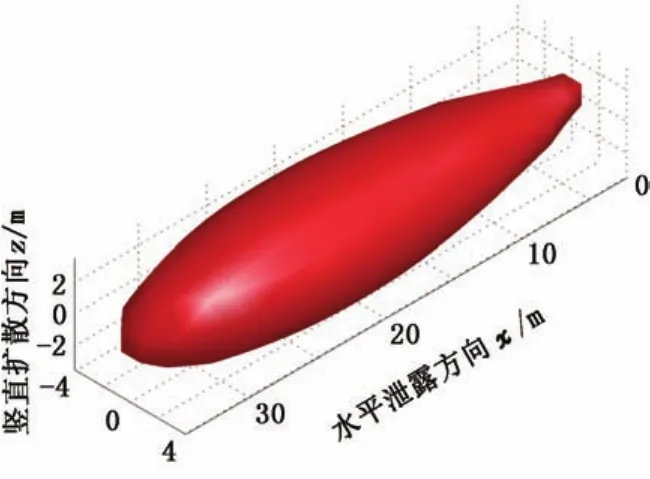
图1 水平方向管道泄漏扩散模型Fig.1 Horizontal pipeline leakage diffusion model

不同管道内压时天然气泄漏扩散数据见表1。

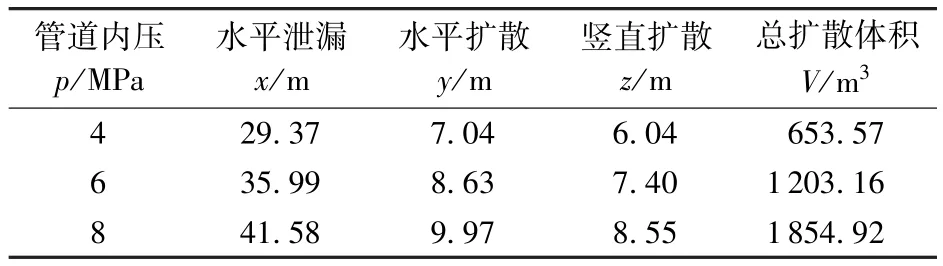
表1 不同管道内压天然气泄漏扩散数据Table 1 Natural gas concentration diffusion data over different internal pressure

1.4 TNT当量法

TNT当量法原理是把气云爆炸的破坏作用转化成TNT爆炸的破坏作用,从而把蒸气云的量转化成TNT当量。TNT当量法关键模型：

式中,WTNT、Wf分别为蒸气云的TNT当量、燃料总质量,kg;Qf、QTNT分别为蒸气的燃烧热与TNT的爆炸热。

以内压p=6 MPa为基本模型,其浓度达到爆炸最低浓度5.3%的总扩散体积为1 203.16 m3,天然气密度0.717 kg/m3,则天然气爆炸总质量为862.67 kg。遵循最危险原则,取爆源释放率为5%,即天然气真实爆炸质量为Wf=862.67×5%=43.13 kg。根据TNT当量法,取天然气燃烧热值Qf=54 MJ/kg,得泄漏天然气TNT当量值WTNT=20.70 kg。

2 爆炸控制方程及数值模拟

2.1 控制方程

通过TNT当量法计算出泄漏天然气TNT当量值WTNT=20.70 kg。已知TNT密度为1.63×103kg/ m3,则TNT球半径为144.76 mm。

TNT爆轰速度为6.930 km/s,C-J压力为21 GPa,爆轰产物状态方程采用JWL方程[10],该状态方程可以用来计算爆炸中由化学能转化成的压力。其压力和能量的关系可确定为

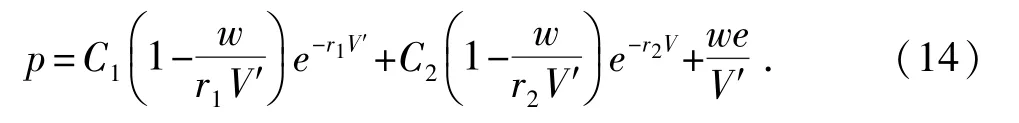
式中,V′为炸药相对体积;e=4.29 MJ/kg为炸药初始比内能;C1、C2、r1、r2和w为材料常数。

炸药TNT的材料参数可以假定为：C1=373.77 GPa,r1=4.15,C2=3.7471 GPa,r2=0.9,w=0.35。

数值计算中,初始温度T=300 K,空气的材料模型假设为理想气体EOS Ideal Gas模型,其Ideal Gas状态方程为

式中,R为理想气体常数;ρ为空气密度。

其压力p和能量E的关系可确定为

取空气密度ρ=1.225 kg/m3,绝热指数k=1.4,为保证周围环境空气为一个标准大气压(101.332 kPa）,将空气的初始内能设为E=206.8 J/mm3。

2.2 物理模型

利用Ansys Workbench建立Pipeline-Solid和GAS-Fluid模型,材料选取修正的STEEL4340,管道网格划分单元大小为80,用GAS模型网格进行局部划分。通过Explicit Dynamics模块导入Autodyn软件,加入空气和TNT材料,建立Space的Euler-FCT模型。物理模型示意图和变形探测点见图2、3。其中两管道中心间距S2分别设置为2、3、4、5、6、7 m。架空天然气管道周围无障碍物,将IdeaGas未与TNT球直接接触表面的四个边界均设置成Flow out模式,以保证能量的流动特性。管道内壁内压为6 MPa,管道z=0端轴向位移vz=0 m/s。

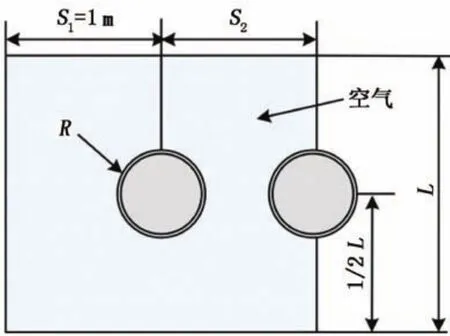
图2 物理模型示意图Fig.2 Schematic diagram of physical model

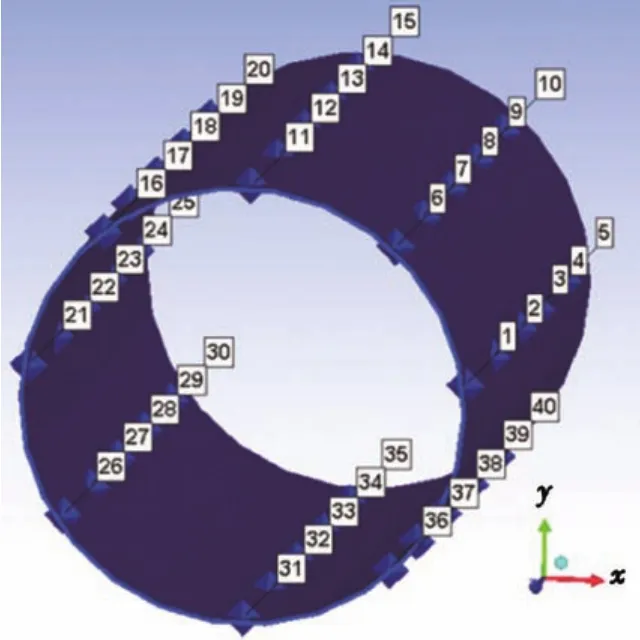
图3 探测点分布图Fig.3 Gauge points distribution

3 结果分析

3.1 数值模拟结果

以并行间距3 m系列为例,通过对整体管道受爆炸冲击的变形量进行分析确定最大变形位置。并以此位置的探测点为基本点,整体分析全部并行间距系列的最大变形量,进而确定不同并行间距下管道受冲击破坏程度。

因为管道在z轴方向呈vz=0 m/s固定形式,这里只观测x轴、y轴两个方向探测点的位移变化量。各系列探测点的位移随时间变化的最值见图4。其对应的冲击超压最值曲线见图5。

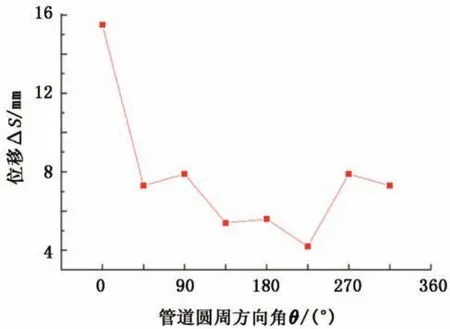
图4 探测点位移最大值Fig.4 The maximum displacement of gauge points

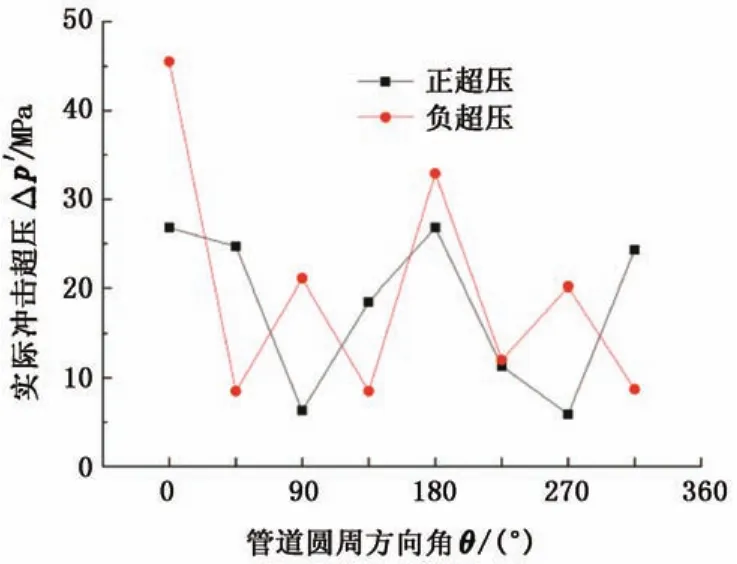
图5 管道圆周方向所受实际冲击超压曲线Fig.5 Actual explosion overpressure curves of pipe direction circumference

探测点1～5系列为管道正对爆炸源位置,所受爆炸冲压最大,正压达26.8 MPa,亦是管道最大变形位置,这是由冲击波传播过程中的正反射规律所致。另外由于冲击波存在环流作用,波阵面绕过管道顶部和底部向后传递时,管道正对爆炸源位置形成真空,负压达45.5 MPa。管道背面与爆炸源处在同一水平面上的位置,即探测点21～25系列,其所受正负超压接近1～5系列,亦是由冲击波环流作用造成的。

对并行间距3 m系列管道受爆炸冲击的超压和变形量进行分析。结合冲击波对管道破坏规律,选定探测点1～5和21～25系列为基本探测点,对不同并行间距上基本探测点的位移、速度和所受超压进行管道变形分析。不同并行间距下冲击超压最值曲线见图6,探测点1、21的位移最大值见图7。

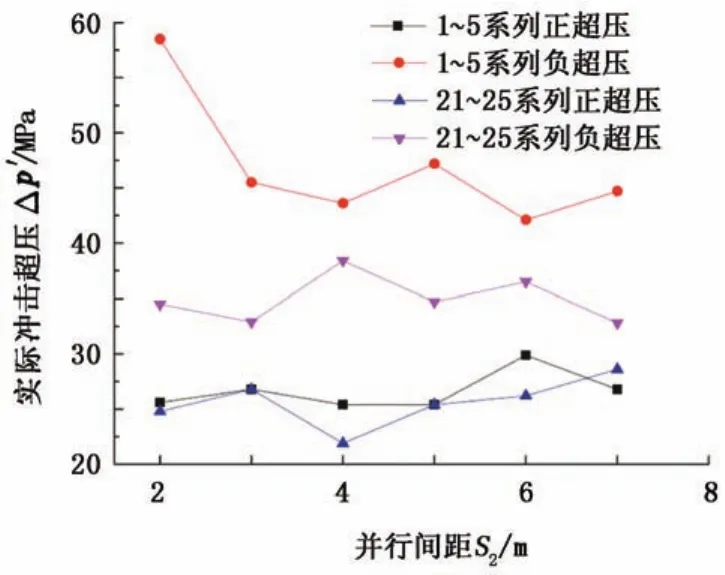
图6 不同并行间距下实际冲击超压Fig.6 Actual explosion overpressure at different parallel distance

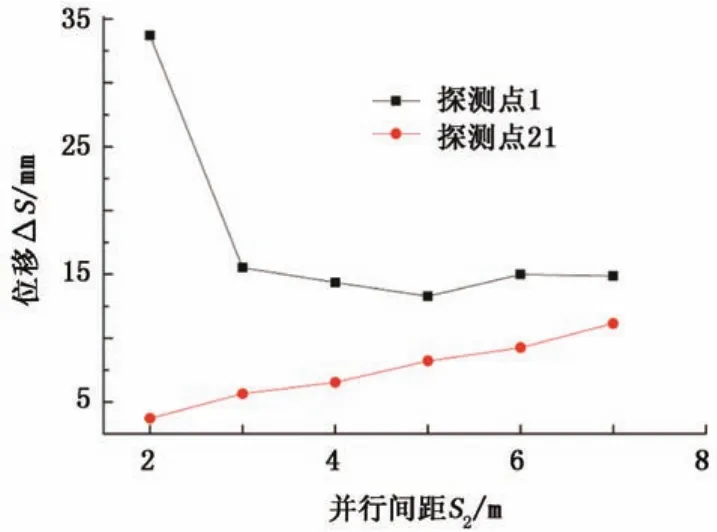
图7 不同并行间距下探测点1和21位移最大值Fig.7 The maximum displacements of gauge points 1 and 21 at different parallel distance

管道正对爆炸源部位的变形量随着并行间距的增加逐渐降低,最大变形值在2 m间距系列达33.7 mm。自并行间距3 m系列开始,管道变形量大幅降低至15 mm,之后随着并行间距的增加,其管道变形量保持在12～15 mm。其变形特点为：并行间距在2～3 m时,管道受冲击产生的破坏形式同时包括超压破坏和冲量破坏,超压破坏造成管道的大幅变形,即超压破坏起主导地位;并行间距在3～4 m时,变形时间长,说明其变形受超压破坏和冲量破坏同时作用。管道爆炸对并行管线的冲击效应大幅降低,冲击波超压开始向四周均匀扩散,无法对管道形成集中超压破坏,管道所受冲量破坏略大于超压破坏;并行间距大于4 m后,管道受管线爆炸产生的变形主要由爆轰波超压破坏所致,后续的冲量破坏对管道变形不起决定性作用。

3.2 超压理论计算公式

气体爆炸产生的冲击波在前进过程中遇到管壁会发生正反射、斜反射、叠加和环流等现象,其超压峰值远大于自由场的压力,破坏效应明显。计算表明,当强入射冲击波在刚性壁面上发生反射时,仅正反射波阵面上的压力即可达到入射冲击波阵面压力的8倍[11]。

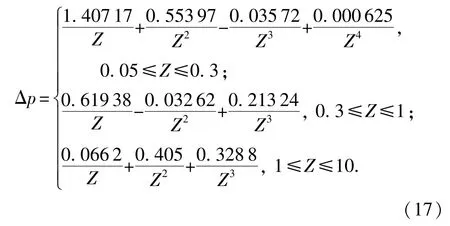
以并行间距2 m为例,采用Henrych经验公式计算冲击波峰超压。因实际冲击波传播间距须减去管道半径,即1.39 m,则爆炸特征长度z=0.506,代入式(17）得冲击超压Δp=2.689 MPa。因冲击波存在正反射、斜反射和叠加等现象,实际冲击超压取保守估计：Δp′=9Δp=24.68 MPa。由图6可得,并行间距2 m时探测点1～5系列数值计算所得超压为25.6 MPa,该值与探测点所受正超压均值误差为

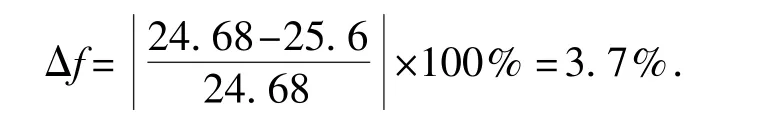
并行间距2 m时模拟值与理论值十分吻合,误差在5%以内,说明利用Autodyn模拟管道爆炸冲击过程是可行的,数值结果具有较高置信度。

3.3 管道受冲击失效风险评价

由于管道背部最大变形量小于正面变形量,以管道正面变形量为参考值,判断管道变形的风险。采用管道应变设计准则分析管道受冲击的失效风险。

基于应变的管道椭圆化设计准则[13]为

式中,Δθ为无量纲椭圆度;Dmax、Dmin分别为管道外径最大值和管道内径最小值;Δθcrit为临界无量纲椭圆度,这里取Δθcrit=3%。

将各并行间距系列的管道变形量代入式(17）,当并行间距分别为2、3、4、5、6、7 m时,其椭圆度分别为5.52%、2.50%、2.35%、2.18%、2.46%和2.44%。

只有在并行间距为2 m时,管道变形超出椭圆极限;并行间距不小于3 m时,管道变形程度未超出椭圆极限。但考虑到爆炸后管道的后燃烧效应及并行间距小于5 m时管道所受冲击破坏以冲量破坏为主,管道依然存在运行风险。并行间距大于等于5 m时,管道受爆炸冲击后存在超压破坏风险,但变形量未超出应变极限规定,运行风险低。

4 结 论

(1）架空管线受并行天然气管线爆炸冲击产生的变形破坏为超压破坏和冲量破坏两种形式。

(2）验证了数值计算方法的可行性,其结果有较高置信度。

(3）架空管道大变形位置为正对爆炸源最近点和背对爆炸源最远点。其变形原因在t=20 ms之前以超压破坏为主;20 ms之后,若并行间距小于等于4 m,大变形仍受冲量破坏影响;若并行间距大于4 m,可忽略冲量破坏对管道的变形作用。

(4）并行安全间距分为：一级风险距离为0～2 m,此并行距离内管道极易发生大变形破坏。若管道敷设环境苛刻,对于V形沟等狭长地带,至少须保证2 m的并行间距;二级风险距离为2～5 m,该并行间距下管道受爆炸冲击产生的破坏风险较低,但考虑到后燃烧效应,尽量避免将并行间距设置在此范围;三级风险距离为5 m以上,在此并行间距下管线爆炸基本不会对并行管线产生破坏效应。

[1] 戚爱华.我国油气管道运输发展现状及问题分析[J].国际石油经济,2009,17(12）：57-59.

QI Ai-hua.Present development situation and problem analysis of oil and gas pipeline in our country[J].International Petroleum Economics,2009,17(12）：57-59.

[2] 张华,赵新伟,陈娟利,等.并行管道风险因素与事故交互作用分析[J].管道技术与设备,2010,5：52-55.

ZHANG Hua,ZHAO Xin-wei,CHEN Juan-li,et al. Risk and accident interaction analysis of parallel pipelines [J].Pipeline Technique and Equipment,2010,5：52-55.

[3] 许砚新,马学海,庞宝华,等.天然气管道与原油管道并行敷设的安全间距[J].油气储运,2011,30(11）： 816-818.

XU Yan-xin,MA Xue-hai,PANG Bao-hua,et al.Nature gas pipeline security laying distance with parallel oil pipeline[J].Oil&Gas Storage and Transportation, 2011,30(11）：816-818.

[4] CDP-G-OGP-PL-001-2010-1油气管道并行敷设设计规定[S].北京：中国石油天然气股份有限公司天然气与管道分公司,2010-01.

[5] LEIS B N,PIMPUTKAR S M,GHADIALI N D.Line rupture and the spacing of parallel lines[G]//Max Toch PRCI Publication,Virginia：Pipeline Research Council International,2002.

[6] 向波.并行管道安全间距及保护措施研究[J].天然气与石油,2009,27(3）：1-4.

XIANG Bo.Research of parallel pipeline safety spacing and protection[J].Natural Gas and Oil,2009,27(3）： 1-4.

[7] 朱彦凝.高压天然气管道孔口泄漏扩散浓度与范围仿真探讨[J].安全,2009,30(4）：4-7.

ZHU Yan-ning.Simulation of high pressure natural gas pipeline orifice leakage diffusion concentration and scope [J].Safety,2009,30(4）：4-7.

[8] ERMAK D L,CHAN S T,MORGAN D L,et al.A comparison of dense gas dispersion model simulations with burro series LNG spill test results[J].Journal of Hazardous Materials,1982,76(6）：129-160.

[9] CHAN S T,ERMAK D L.Morris FEM3 model simulations of selected Thorney Island phase I trials[J].Journal of Hazardous Materials,1987,16(3）：267-292.

[10] JACOBS S J.On the equation of state for detonation products at high desity：12th Symposium(International）on Combustion[C].Pittsburgh：The Combustion Institute,c1969.

[11] 宁建国,王成,马天宝.爆炸与冲击动力学[M].北京：国防工业出版社,2010：110-113.

[12] 杨鑫,石少卿,程鹏飞.爆炸冲击波在空气中传播规律的经验公式对比及数值模拟[J].岩土工程,2007, 27(5）：71-73.

YANG Xin,SHI Shao-qing,CHENG Peng-fei.The empirical formulas and numerical comparison of explosion shock wave in air[J].Geotechnical Engineering,2007, 27(5）：71-73.

[13] DNV-OS-F101.Submarine pipeline systems[S].Norway：DET NORSKE VERITAS,2010.

(编辑 沈玉英）

Safe distance of overhead parallel pipeline calculated by numerical simulation of gas pipeline explosion

WANG De-guo
(College of Mechanical and Transportation Engineering in China University of Petroleum,Beijing 102249,China）

Based on the explosion phenomenon caused by natural gas pipeline failure,leakage model of overhead pipeline was established by theoretical analysis method.The volume of gas participating in the blast was calculated by Matlab software,and the initial volume values of pipe explosion model couod be converted to equivalent by TNT equivalent method.In addition,pipe explosion physical model was established by Autodyn software,and the explosion overpressure and deformation impacted on the parallel pipeline were calculated over different parallel pipeline spacing.According to the pipe ellipse strain criterion,the impact deformation risk was assessed over different parallel pipeline spacing.The results show that the deformation failures of overhead lines are the overpressure and impulse damage failures in two forms.The deformation position of overhead pipeline is the nearest point facing explosive source and the farthest point back to explosive source.The safe overhead parallel spacings are obtained.The spacing less than 2 m is the first risk distance,the secondary risk distance is spacing from 2 m to 5 m,and the third risk distance is spacing more than 5 m.The comparison between the numerical simulation results and the theoretical calculation results verifies the feasibility of the numerical method.

parallel pipeline;TNT equivalent method;pipeline explosion;parallel spacing

TE 973;TE 88

A

1673-5005(2013）05-0175-06

10.3969/j.issn.1673-5005.2013.05.025

2013-06-18

国家科技支撑计划课题(2011BAK06B01）;质检公益性行业科研专项(201010025）

王德国(1962-）,男,教授,博士生导师,从事机械工程的教学与科研工作。E-mail：wdg@cup.edu.cn。