管道钢裂纹扩展阻力曲线测试研究

帅 健

(中国石油大学机械与储运工程学院,北京 102249）

管道钢裂纹扩展阻力曲线测试研究

帅 健

(中国石油大学机械与储运工程学院,北京 102249）

采用多试样法测试X65和X80两种管材的R曲线、启裂韧性及撕裂模量,对比分析R曲线参量的塑性铰模型法和η因子法。结果表明：塑性铰模型法和基于载荷-裂纹嘴位移曲线的η因子法的测试结果比较接近,基于载荷-加载线位移曲线的η因子法与前两种方法的差别较大;对于中等强度的X65管材,塑性铰模型法、基于载荷-裂纹嘴位移曲线和载荷-加载线位移曲线的η因子法得到的R曲线较为一致,而对高强度的X80管材,这3种方法得到的R曲线偏差较大,特别是δ-R曲线的分散性较高;基于R曲线的撕裂模量趋于稳定,展现了裂纹的稳态扩展特性。

管道钢;断裂韧性;阻力曲线;多试样法;η因子法;塑性铰模型

应用高强度高韧性管道钢的高压大口径输气管道的轴向裂纹的长程扩展是其主要失效模式之一,往往会造成灾难性的后果,因此对高压管道的断裂控制非常重要[1-2]。裂纹扩展阻力曲线(R曲线）能描述任何材料的断裂行为。Krafft等[3]提出用K或Keff代替依赖于尺寸变化的KC作为R曲线的代表性参数。Zerbst[4]对K-R曲线测试方法进行了分析总结,编制了测试标准ASTM E561,最新版为ASTM E561-2005[5],该标准不同于ASTM E399-1990[6]之处在于取消了对试样最小厚度的限制,但对裂纹扩展长度仍有限定。K-R曲线的缺点为：①裂尖塑性区以弹性为主,Keff可以存在小范围的塑性屈服;②对试件有严格的尺寸要求。ASTM E813-1981[7]首次采用多试样法获取J-R曲线评估断裂韧性,随后,Joyce[8]提出了单试样卸载柔度法,该方法被ASTM E1152-1987采用[9]。Anderson[10]对CTOD (crack tip opening displacement）作为断裂韧性参数的研究作过详细的回顾。最早的CTOD测试标准是BS 5762-1971[11],随后,改版为BS 7448-1991[12],其中组合了K、J和CTOD的测量方法,最新修订版为BS 7448-2005[13]。ASTM[14]发布了CTOD的测试标准ASTM E1290-1989,最新版为ASTM E1290-2008[15]和E1820-2008[16],两者的区别在于后者给出更标准化的CTOD阻力曲线测试方法。ASTM[17]和ISO[18]分别发布了低约束条件下稳态裂纹扩展的断裂韧性测试标准ASTM E2472-2006和ISO 22889-2007,提出了薄壁试样的δ5-R曲线测试方法。R曲线的测试标准应用于高强度管道钢存在一定问题。例如,同一材料、同一试样使用不同标准得到的阻力曲线出现较大差别,采用J-R曲线表征高强度高韧性管道裂纹扩展能力的适用性和有效性仍不确定[19-20]。笔者采用多试样法对X65和X80钢级管道的J-R曲线或δ-R曲线进行研究,测定两种管材的R曲线及断裂韧性,研究管道钢强度级别提高对断裂韧性测试的影响。

1 测试方法

R阻力曲线的测试标准主要有BS 7448-2005[13]、ASTM E1820-2008[16]、ISO 12135-2002[21]和ASTM E2472[17],测量参数为J积分或CTOD。CTOD计算方法有两种：一种为塑性铰模型,另一种采用基于载荷-位移曲线围线面积的η因子法,计算公式为

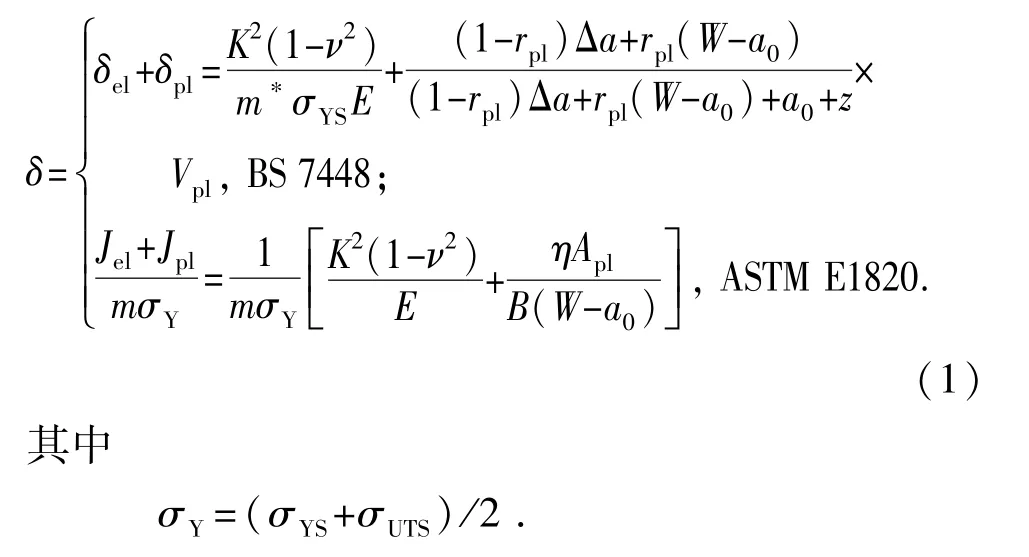
式中,Jel和Jpl分别为J积分的弹性和塑性分量;δel和δpl分别为δ的弹性和塑性分量;K为应力强度因子;σYS为材料屈服应力;σY为有效屈服应力;σUTS为材料拉伸极限应力;E为弹性模量;ν为泊松比; W、B、a0、z为试样的几何参数;rpl为旋转因子;rpl(W -a0）为旋转中心到裂尖距离,在BS 7448-2005标准中,规定对三点弯SENB试样,rpl=0. 4;Vpl为载荷-裂纹嘴位移(F-CMOD）曲线中的塑性位移;Apl为载荷-加载线位移(F-VLL）曲线中的塑性面积;m*为一常数;平面应力取1.0,平面应变取2.0。

m和η都是与试件几何尺寸相关的量,为(a0/ W）的函数,表示为

式中,C(T）(compact tension）为紧凑拉伸试件。

在不同标准中,对SENB试样的η因子计算公式不同,例如,ASTM E1820中规定,当选用载荷-加载线位移曲线计算CTOD时,η=1.9。如果为载荷-裂纹嘴位移曲线,η计算为

至于裂纹扩展量,多试样测试法中采用试验后打断试件直接测量,如九点测量取平均值;单试样法中利用卸载柔度法反推求裂纹扩展长度。

2 测试过程

试样取自于实际管道,X65和X80的直径分别为864、1219 mm,厚度分别为11.8、18 mm,设计压力分别为8.5、12 MPa。试验得到两种管材的应力/应变曲线见图1,力学性能参数见表1,两种管材为典型的高塑性钢材。从图1中可以看出,X65管材存在明显的屈服平台,且塑性变形量远远大于X80的。虽然X80管材有较高的屈服极限,但其屈服强度比大于0.9,应变硬化能力较差。

采用标准三点弯SENB试样和紧凑拉伸试样C (T）,试样在管道上的取样方向见图2,试样加工依据BS 7448-2005和ASTM E1820-2008。X65管道加工了SENB和C(T）两种试样,X80管道仅SENB一种,每种试样制备10个,共3组。对试样进行疲劳预制裂纹,如SENB试样最大疲劳裂纹预制力约3.5 kN,循环次数大约在20000～30000。预制疲劳裂纹后的试样初始裂纹长度a0=0.5 W,应力比小于0.1。

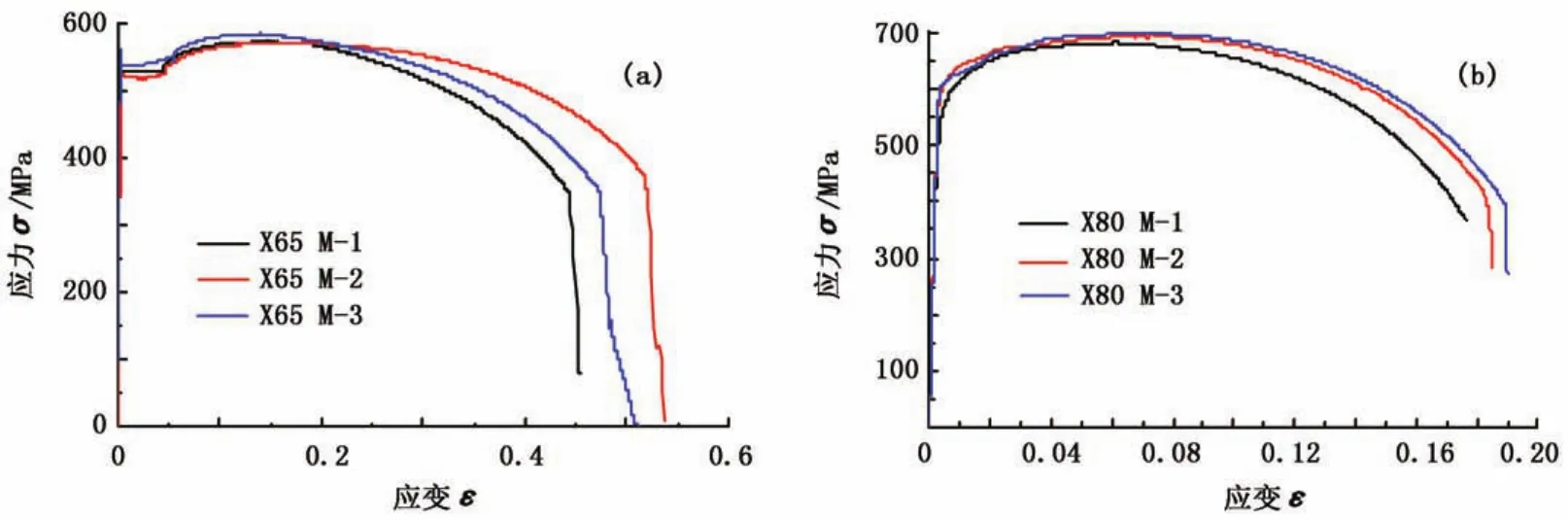
图1 X65和X80管材拉伸应力应变曲线Fig.1 Tensile stress-strain curves for X65 and X80 steels

表1 X65和X80管材机械性能Table 1 Mechanical properties of X65 and X80 steels

图2 SENB和C(T）试样取样图Fig.2 Sampling diagram of SENB and C(T）specimens

在MTS 810-250型液压伺服试验机上进行试验,SENB试样安装过程中加载线的长度应与两辊中心间距相等,误差不超过1%(0.8 mm）。试样安装时的跨距s(4W±1%）要保证压头、试样裂纹和跨距的中心线三线合一。

采用多试样法对每组10个试样各自加载到不同位移,以产生不同的稳定裂纹扩展长度,绘制材料阻力曲线。采用位移控制加载模式,加载速率为0.5 mm/min,记录载荷、位移、时间和CMOD四个参数。首先将第一个试样加载到接近最大载荷平台起始点,然后卸载,计算裂纹扩展长度,依据第一个试样的裂纹扩展情况估计其他试样的加载停机点,以保证试验数据点的均匀分布。

试验后,对试样进行热着色或二次疲劳,标识裂纹扩展位置,打断试样,采用“九点法”测量裂纹扩展长度Δa。测量过程中,应辨别预制裂纹区、延伸区和裂纹扩展区。测量仪器的准确度应不低于± 0.1%或0.025 mm。

3 结果及其分析

各试样加载到不同位移水平,其载荷-加载线位移曲线见图3、4。

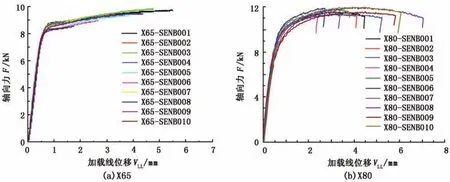
图3 SENB试件载荷-线位移曲线Fig.3 Load-line displacement curves of SENB specimens

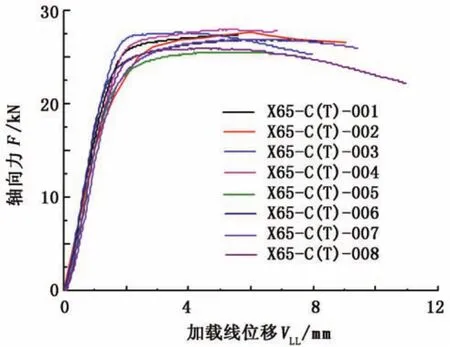
图4 C(T）试件载荷-加载线位移曲线Fig.4 Load-line displacement curves of C(T）specimens

从图中可以看出,其曲线走势基本一致,除X65管道的C(T）试样载荷曲线分散性较大外,其他曲线分散性都很小。X65管道SENB与C(T）试样最大载荷分别为(7.5±0.5）kN和(26.5±1.5）kN, X80管道SENB试样最大载荷为(10.5±0.4）kN。加载过程中X80管道的个别试样出现了载荷微小突降,其他试样均未出现这种现象。

图5为BS7448塑性铰模型的计算结果。对于X65管道,C(T）试样的δ-R曲线高于SENB试样的;而启裂后两曲线趋势基本相同,对于给定裂纹扩展量,X65管道的SENB和C(T）试样的启裂韧度分别为=0.42和=0.54,两曲线的δ相差大约0.12 mm。两种试样在启裂点的J积分值相差很小,=345 kJ/m2,=376 kJ/m2。启裂后SENB试样有更低的J值。与X65管材相比,X80有更高的δ和J值,X80管道的δ和J启裂韧度分别为：=0.67,=499 kJ/m2。启裂后两种材料的δ-R曲线基本平行,相差大约0.25 mm。但是,对于J-R曲线,随着裂纹扩展量增加X80与X65之间的J积分差值增大。

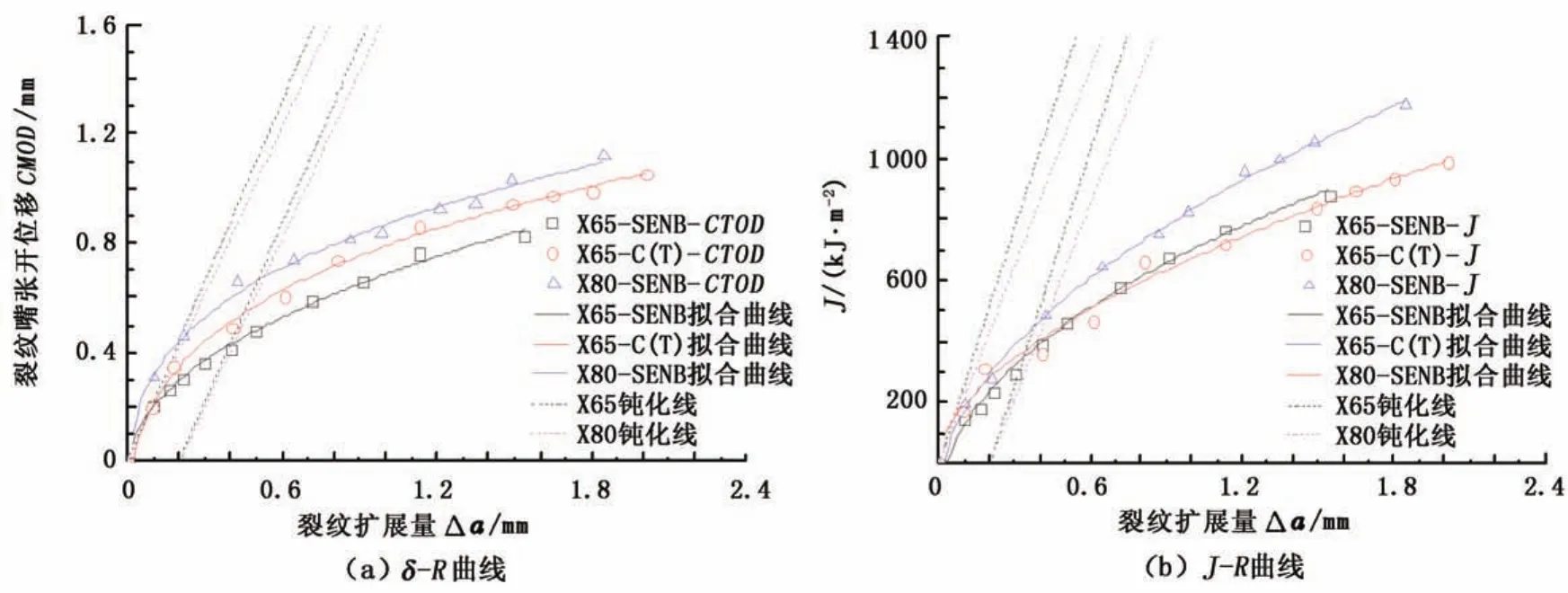
图5 基于塑性铰模型的R曲线Fig.5 R-curve based on plastic hinge model

试验中,主要的记录数据为载荷、加载线位移(VLL）、裂纹嘴张开位移(CMOD）和裂纹扩展量(Δa）。F-VLL曲线或F-CMOD曲线下的塑性面积Apl是η因子法计算J积分的最重要参数。根据这两种曲线分别计算了X65和X80试样的J积分见图6、7。由图6可看出：①X65-C(T）试样基于FVLL曲线得到的CTOD和J值与SENB试样的相差甚大,并且已超过X80管材SENB试样得到的CTOD和J值;②通过J积分计算结果转化得到CTOD值可信度较低,例如,图6(a）中的X80管道SENB试样在启裂点后的δ甚至低于X65管道SENB试样的。

与图6相比,图7中基于F-CMOD曲线得到的CTOD与J的准确度较高。图7中显示,X65管道SENB与C(T）试样的断裂韧性基本一致。当裂纹扩展量Δa＜1 mm时,X80管道的CTOD高于X65的,但裂纹扩展量超过1 mm后,X80管道的CTOD又低于X65的,主要原因为X65比X80有更好的延展性。由于X80的有效屈服应力较高,其J积分值高于X65的对应值,比较两种材料的CTOD-R与JR曲线斜率,X65的R曲线斜率均大于X80的。

F-VLL、F-CMOD曲线以及塑性铰模型3种方法得到的δ-R和J-R曲线对比见图8。从图8中可以看出,对于X65管材,这3种方法计算得到的断裂韧性基本一致;而对于X80管材,3种方法得到的R曲线的差别较大,尤其δ-R曲线的分散性更大。这也说明,随着管材强度提高,R曲线测试方法的准确性降低,因此,有必要改进现有R阻力曲线测试方法,改善测试方法的一致性。

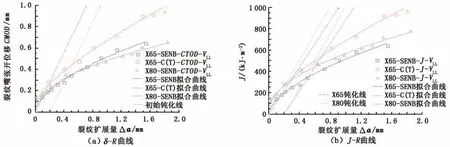
图6 基于F-VLL曲线的η因子法计算的R曲线Fig.6 R-curves calculated by η factor method based on F-VLLdata

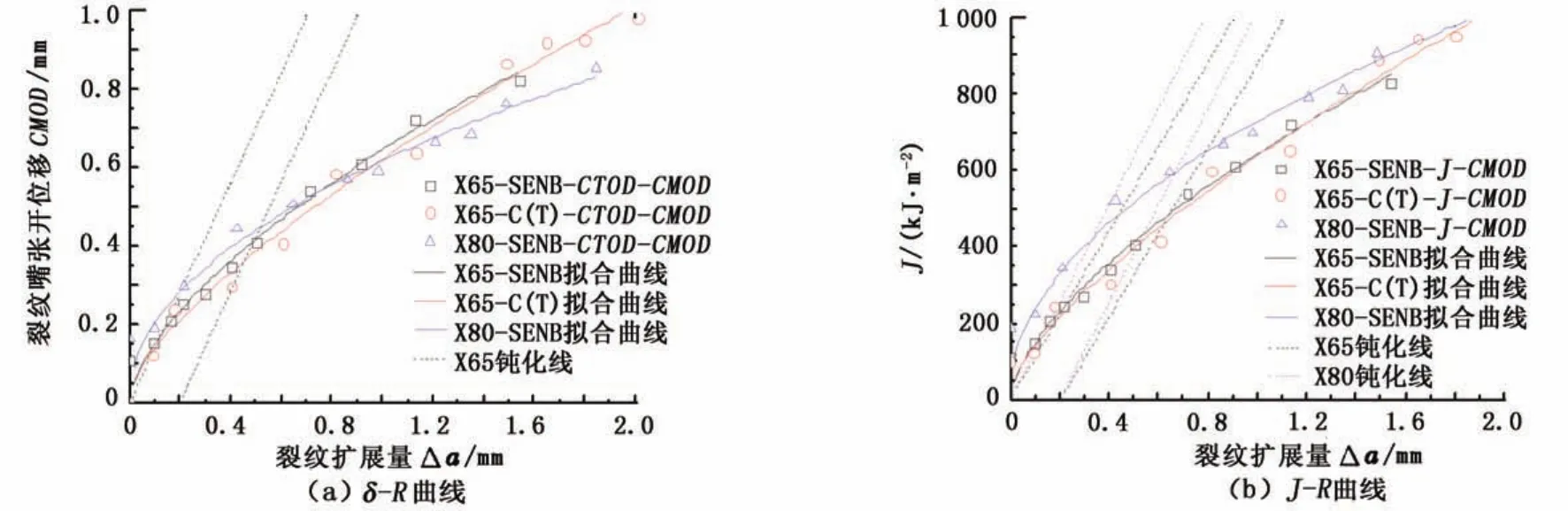
图7 基于F-CMOD曲线的η因子法计算的R曲线Fig.7 R-curves calculated by η factor method based on F-CMOD data

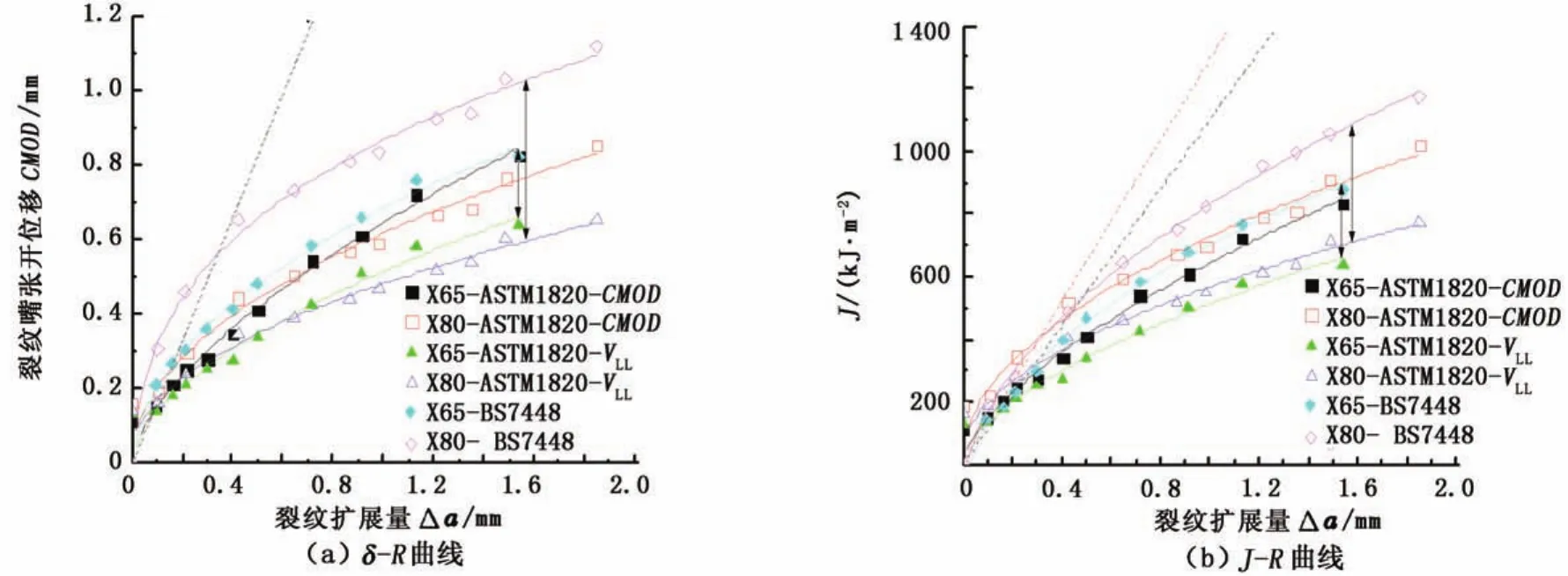
图8 塑性铰模型与η因子法计算的R曲线对比Fig.8 Comparison of R curves calculated by plastic hinge model and η-factor method

X65管材SENB和C(T）试件的R曲线对比见图9。从钝化到启裂,C(T）与SENB试样的R曲线均一致,断裂韧性值相差很小。随着裂纹扩展量的增加,C(T）试样的R曲线逐渐趋于一条线,扩展变为稳定;但SENB试样却相反,R曲线分散性随裂纹扩展量增加而增大。这是因为,与SENB试样相比, C(T）试样有较长裂纹扩展长度,可以一定程度上反映裂纹扩展特性;而SENB试样具有的裂纹扩展长度较短,不适合于裂纹扩展,仅反映裂纹的启裂韧性。

表2列出了X65和X80试样的裂纹稳定扩展下限临界值δIC和JIC,其中,δIC和JIC为稳定裂纹扩展量0.2 mm钝化偏置线时对应的非尺寸敏感断裂韧性。基于所有测试数据拟合X65和X80管材的裂纹扩展阻力曲线见式(7）～(10）。X65取SENB和C(T）试样的平均值,启裂韧度为：δIC=0.42 mm,JIC=425 kJ/m2;X80的启裂韧性为：δIC=0.49 mm,JIC=504 kJ/m2。

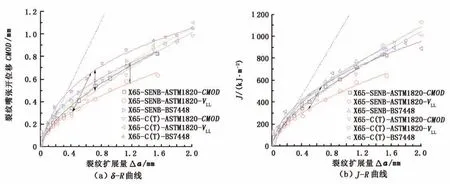
图9 X65钢C(T）和SENB试样的R曲线Fig.9 R curves of C(T）and SENB specimens for X65 steel

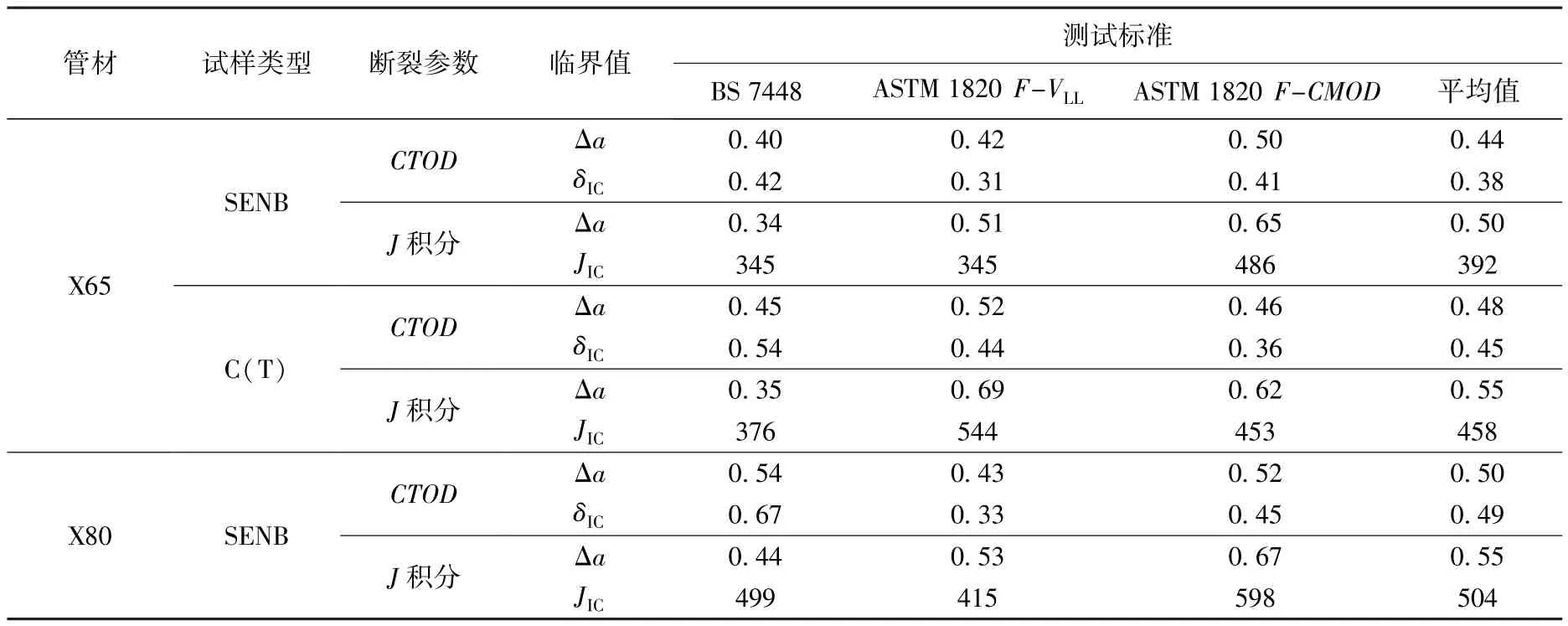
表2 X65与X80管材断裂韧性Table 2 Fracture toughness of X65与X80 steel

当裂纹扩展一定量后,R曲线的斜率可以显示出材料的稳定裂纹扩展特性,斜率较大的R曲线相对难以失稳扩展。对于J-R阻力曲线,通常用撕裂模量TR量化R曲线的斜率,该参数是一无量纲参数。X65管材不同试样及不同方法得到的TR曲线如图10所示。启裂阶段撕裂模量较高,之后逐渐减小至稳定。这也说明,R曲线不但可以反映裂纹启裂特性,也能表征裂纹扩展特性。从图10还可以看到,不同试样及不同方法得到的撕裂模量曲线基本一致,其中最小撕裂模量为C(T）试样由BS7448标准求得的J-Δa曲线的临界斜率,约为175。

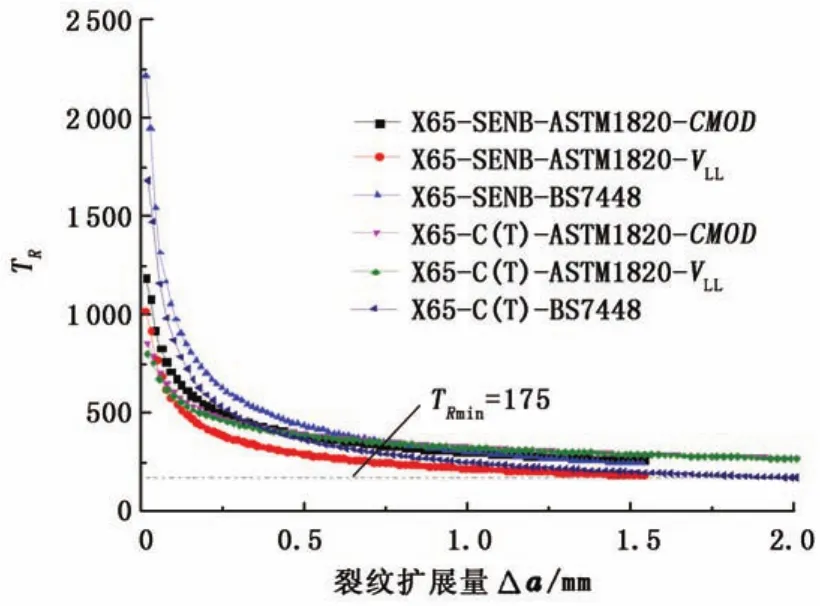
图10 X65两种试样的TR曲线对比Fig.10 Comparison of TRcurves for two kinds of X65 specimens

4 结 论

(1）试验测定X65的启裂韧度为δIC=0.41 mm,JIC=425 kJ/m2;X80的启裂韧度为δIC=0.49mm,JIC=504 kJ/m2。

(2）对于同一种管道钢,SENB和C(T）两种标准试样测得的启裂韧性相同,其中,C(T）试样具有一致的稳态裂纹扩展曲线,较适用于测试管道钢的裂纹扩展特性。

(3）塑性铰模型法和基于载荷-裂纹嘴位移曲线的η因子法基本等效,相比之下,用载荷-加载线位移曲线得到的R曲线与前两种方法的差别较大。

(4）对于X65管材,塑性铰模型法与基于载荷-裂纹嘴位移曲线、载荷-加载线位移曲线的η因子法3种方法得到的R曲线较为一致;而对X80管材,这3种方法得到的R曲线偏差较大,特别是δ-R曲线的分散性较高,有必要改进高强度管材的R阻力曲线测试方法。

(5）基于R曲线的撕裂模量在启裂阶段的数值较大,启裂之后,逐渐减小并趋于稳定,反映了裂纹的稳定扩展特性。

[1] 帅健.管线力学[M].北京：科学出版社,2010：30-49.

[2] 李方坡,韩礼红,刘永刚,等.高钢级钻杆韧性指标的研究[J].中国石油大学学报：自然科学版,2011,35 (5）：136-139.

LI Fang-po,HAN Li-hong,LIU Yong-gang,et al.Investigation on toughness index of high grade steel drill pipe [J].Journal of China University of Petroleum(Edition of Natural Science）,2011,35(5）：136-139.

[3] KRAFFT J M,SULLIVAN A M,BOYLE R W.Effect of dimensions on fast fracture instability of notched sheets [C]//Kennedy A J.Proceedings of the Symposium on Crack Propagation.UK：Cranfield,1961：8-28.

[4] ZERBST U,HEINIMANN M,DONNE C D,et al.Fracture and damage mechanics modelling of thin-walled structures—an overview[J].Engineering Fracture Mechanics,2009,76：5-43.

[5] ASTM E561-2005 Standard test method for K-R curve determination[S].West Conshohocken：ASTM International,2005.

[6] ASTM E399-1990 Standard test method for linear-elastic plane-strain fracture toughness KICof metallic material [S].West Conshohocken：ASTM International,1990.

[7] ASTM E813-1981 Test method for JIC,a measure of fracture toughness[S].West Conshohocken：ASTM International,1981.

[8] JOYCE J A.Manual on elastic-plastic fracture：laboratory test procedures[M].West Conshohocken,1996.

[9] ASTM E1152-1987 Test method for determining J-R curves [S].West Conshohocken：ASTM International,1989.

[10] ANDERSON T L.Fracture mechanics：fundamentals and applications[M].Boca Raton：CRC Press,2005：326-329.

[11] BS 5762-1979 Methods for crack opening displacement (COD）testing[S].London：British Standards Institution,1979.

[12] BS 7448-1-1991 Fracture mechanics toughness tests-part 1：method for determination of KICcritical CTOD and critical J values of metallic materials[S].London： British Standards Institution,1991.

[13] BS 7448-3-2005 Fracture mechanics toughness tests-part 3：method for determination of fracture toughness of metallic materials at rates of increase in stress intensity factor greater than 3.0 MPa·m0.5s-1[S].London：British Standards Institution,2005.

[14] ASTM E1290-1989 Standard test method for crack-tip opening displacement(CTOD）fracture toughness measurement[S].West Conshohocken：ASTM International, 1989.

[15] ASTM E1290-2008 Standard test method for crack-tip opening displacement(CTOD）fracture toughness measurement[S].West Conshohocken：ASTM International, 2008.

[16] ASTM E1820-2008 Standard test method for measurement of fracture toughness[S].West Conshohocken： ASTM International,2008.

[17] ASTM E2472-2006 Standard test method for determination of resistance to stable crack extension under lowconstraint conditions[S].West Conshohocken：ASTM International,2006.

[18] ISO 22889-2007(E）Metallic materials-method of test for the determination of resistance to stable crack extension using specimens of low constraint[S].Switzerland：ISO,2007.

[19] 韩克江,帅健,王俊强,等.管道大范围屈服断裂评估的研究现状与进展[J].力学进展,2012,42(1）：29-37.

HAN Ke-jiang,SHUAI Jian,WANG Jun-qiang,et al. Research status and progress on fracture assessment of pipeline under condition of large-scale yielding[J].Advances in Mechanics,2012,42(1）：29-37.

[20] 闫相祯,刘锦昆,许志倩,等.服役海底管道钢疲劳可靠性试验与海底管道寿命预测[J].中国石油大学学报：自然科学版,2010,34(5）：113-117.

YAN Xiang-zhen,LIU Jin-kun,XU Zhi-qian,et al. Fatigue reliability test and life prediction of submarine pipeline[J].Journal of China University of Petroleum (Edition of Natural Science）,2010,34(5）：113-117.

[21] ISO 12135-2002 Metallic materials：unified method of test for the determination of quasi-static fracture toughness[S].Switzerland：ISO,2002.

(编辑 沈玉英）

Study on crack growth resistance curve test of pipeline steel

SHUAI Jian
(College of Mechanical and Transportation Engineering in China University of Petroleum,Beijing 102249,China）

The R-curve as well as fracture toughness and tearing module were tested for X65 and X80 steel using multi-specimen method,in which the characteristic parameters were J-integral and CTOD.Plastic hinge model and η factor method were compared.The results show that the test result of plastic hinge model is similar to that of η factor method based on load-crack mouth displacement curves,but has a relative large difference when compared with the test result of η factor method based on load-load line displacement curves.For X65 as mid strength pipeline steel,R curves by plastic hinge model and η factor method based on load-crack mouth displacement curves and load-load line displacement curves,are relatively consistent.However, for X80 as high strength pipeline steel,R curves,especially δ-R curves by the three methods,have a large dispersion.The tearing modulus based on the R curve tend to be a constant,which represents the steady propagation characteristics of crack.

pipeline steel;fracture toughness;resistance curve;multi-specimen method;η factor method;plastic hinge model

O 346.1

A

1673-5005(2013）05-0168-07

10.3969/j.issn.1673-5005.2013.05.024

2013-07-12

高等学校博士学科点专项科研基金项目(20100007110006）

帅健(1963-）,男,教授,博士生导师,主要从事安全科学与工程及工程力学的科研与教学工作。E-mail：sjclass@126.com。