二氧化碳连续管井筒流动传热规律研究

王瑞和,倪红坚

(中国石油大学石油工程学院,山东青岛 266580）

二氧化碳连续管井筒流动传热规律研究

王瑞和,倪红坚

(中国石油大学石油工程学院,山东青岛 266580）

基于二氧化碳在井筒内流动时的传热过程,考察二氧化碳在井筒内的热量和压力传递方式及其对相态和物性变化的影响规律。建立二氧化碳井筒内热传递模型,采用交替方向推进法进行求解,分析二氧化碳在井筒内流动过程中温度、压力和相态的变化规律。结果表明：二氧化碳在连续管内热交换效率较高,温度上升幅度随着井深的增大逐渐减小;二氧化碳沿环空上返过程中,温度逐渐降低,在靠近井口处温度显著下降;随着井深的增大,连续管内的液态二氧化碳逐渐转变为超临界态,在沿环空上返的过程中再次转变为液态,继而变为气液两相至出口。

二氧化碳;连续管;井筒传热;压力损耗

二氧化碳流体与连续管钻井技术相结合可大幅提高钻井效率、有效保护油气藏[1-4],是一项极具应用前景的新型钻井技术。确定二氧化碳在井筒内的热量和压力传递方式及其对相态和物性变化的影响规律,是进行井壁稳定、携岩等相关技术研究和水力参数设计的基础。不同于井筒常规钻井液传热[5-7],以二氧化碳作为循环介质的相关研究[2-8]仍在探索性阶段,主要问题是温度和压力耦合、热阻等尚不明确。笔者基于二氧化碳在井筒内流动时的传热过程分析,建立二氧化碳井筒内热传递模型,分析井筒内二氧化碳温度、压力和相态的变化规律,为二氧化碳连续管钻井技术的进一步发展提供理论依据。

1 二氧化碳井筒内传热模型

1.1 传热模型

二氧化碳作为钻井液进行循环时,热量传递主要为地层与环空流体、环空与连续管内流体间的热交换。为研究方便,假设：①地层温度为线性变化;②传热过程为稳态;③忽略连续管内及环空纵向热量传递。

由于连续管在井筒内无需考虑变径影响及接头处传热变化,任选取微元段如图1所示(其中实线表示流体流动方向,虚线表示热流方向）。

对于该微元段,其总能量方程可表示为

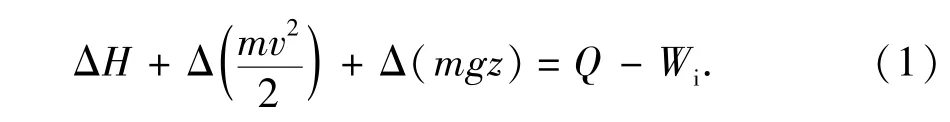
式中,H为焓,J;m为流体的质量,kg;v为流动速度, m/s;Q为吸收的热量,J;Wi为内部功,J。

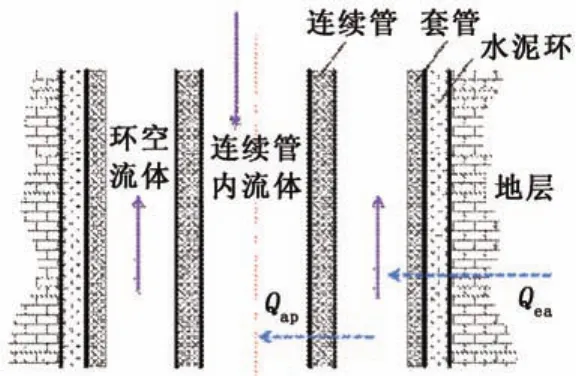
图1 井筒内微元及传热示意Fig.1 Sketch map of finite element and heat transfer in wellbore

因二氧化碳流动过程中对管路不做功,可得Wi= 0;忽略该微元段内物质密度的变化,由质量守恒,速度变化量即可忽略,可得焓变ΔH可写作ΔU+VΔp(式中,ΔU为内能变化量,J;Δp为压力的变化,Pa;V为微元段体积,m3）,因V的变化可忽略,则微元段沿程压力损耗转化的热能亦可略去不计。式(1）可简化为

对于环空中和连续管内的流体,在微元段内其热量变化由式(2）可得

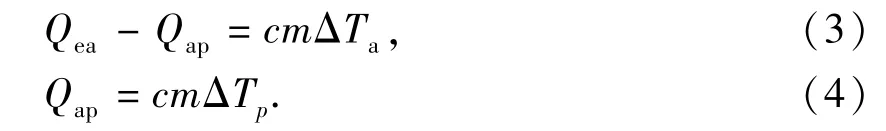
式中,Qea为地层传递给环空流体的热量,J;Qap为环空流体传递给连续管内流体的热量,J;c为流体比热容,J/(kg·K）;ΔTp为连续管管内的温度差,K;ΔTa为微元段环空温度差,K。

地层传热给环空的过程中,热量在套管和水泥环中以热传导方式进行传递,环空流体与套管间由于存在相对运动,为对流传热。因此总热阻包含套管内壁的对流传热热阻以及套管和水泥环的导热热阻,如图2。

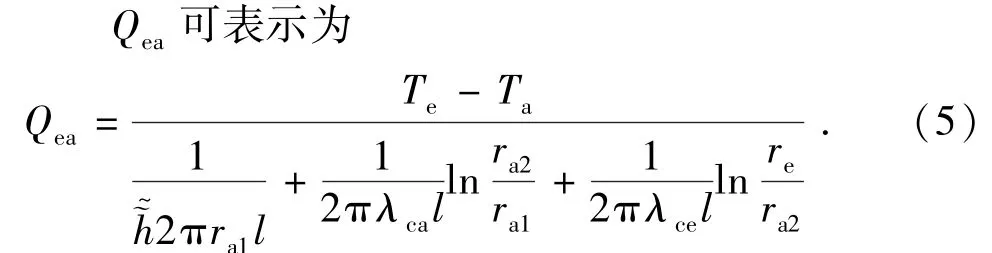
式中,Te为地层温度,K;Ta为环空温度,K;l为微元段长度,m;~h～为环空外壁对流换热系数,W/(m2· K）;re为井筒半径,m;ra2套管外壁半径,m;ra1套管内壁半径,m;λca为套管热导率,W/(m·K）;λce为水泥环热导率,W/(m·K）。

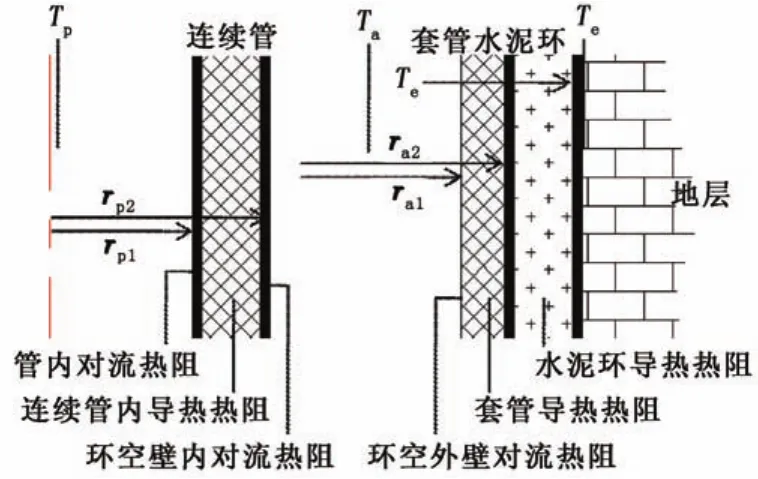
图2 总导热热阻分析示意图Fig.2 Sketch map diagram of overall thermal resistance

对于裸眼井段,因热量传递方式变为环空流与地层的直接对流换热,则Qea可简化为

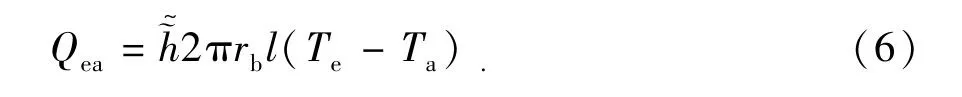
式中,rb为井筒裸眼半径,m。

环空流体与连续管内流体之间的传热介质为连续管管壁,两侧流体均相对管壁移动,热量传递除去连续管管壁导热外,管壁两侧还存在对流传热。因此传热过程中的热阻包括连续管内壁的对流传热热阻,连续管管壁的导热热阻,以及连续管外壁的对流传热热阻,Qap可表示为

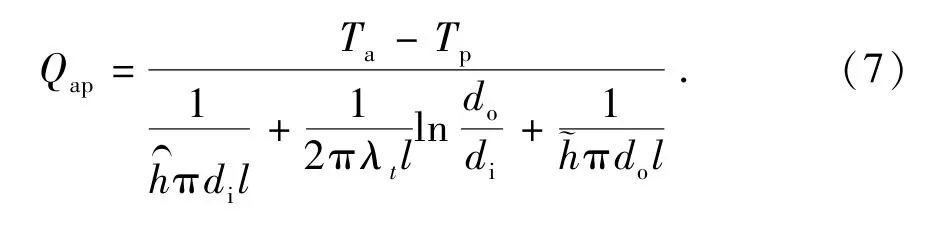
式中,Tp为连续管内温度,K;h为连续管内表面对流传热系数,W/(m2·K）;为环空内壁对流换热系数,W/(m2·K）;do为连续管外径,m;di为连续管内径,m;λt为连续管热导率,W/(m·K）。

1.2 钻头压降和温降

(1）钻头压降：

式中,ΔpB为钻头压降,Pa;m为质量流量,kg/s;C为喷嘴流量系数,无量纲;ρ为流体密度,kg/m3;A为喷嘴面积,m2。

(2）钻头温降：二氧化碳经过钻头水眼,即通过截面缩小的孔道,压力显著下降,产生节流现象。流体在孔口流速很快,与外界进行热量交换一般很小,可以忽略不计,可视为绝热节流过程。节流前后温度发生变化：

式中,ΔT表示节流前后温降,K;p1和p2代表节流前、后的流体压力,Pa;μJT为节流系数。

1.3 环空内外侧对流换热系数

环空内外侧对流传热系数[9-14]是准确计算二氧化碳温度变化的基础,多以Wilson实验法[15]为基础获得经验公式,仅在对流换热系数的修正方法上有所差别。笔者采用数值模拟方法分析二氧化碳在环空内外侧的对流传热,筛选确定可用于分析连续管井筒传热问题的经验公式。针对湍流运动和传热的数学模型采用雷诺时均方程,控制方程为

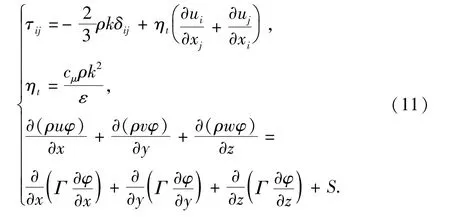
对于固体壁面采用壁面函数法处理。

设定分析用连续管外径50.8 mm,壁厚4 mm,套管外径为127 mm,壁厚11 mm,为消除边界效应取长度为5 m(图3）。

图3 环形空间传热物理模型Fig.3 Physical structure of heat transfer in annuli

边界条件和相关参数：质量流量3～10 kg/s;内管入口温度260 K;环空入口温度280 K;套管壁温度300 K;环空出口为压力;连续管入口为速度;环空入口为速度;连续管内外壁面为耦合。

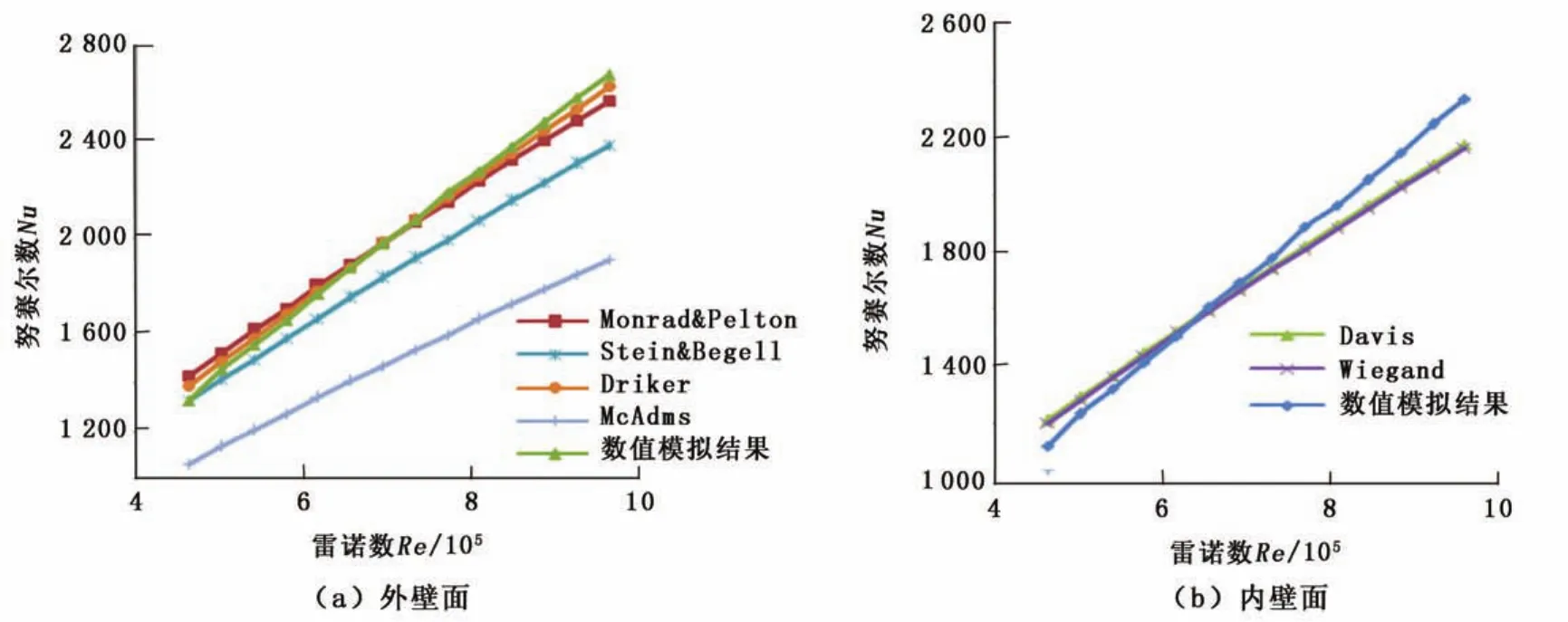
图4 环空内外壁面Nu数随Re数的变化Fig.4 Plot of Nu-Re charm in outer wall of annular tube

图4(a）显示,据Monrad&Pelton[10]、Dirker[11]、 Stein&Begell[12]、Macadams[13]公式和模拟结果计算得到的环形空间外壁面Nu数均随着Re数的增大而增大,但Dirker公式的计算值与模拟结果一致性更好。分析图4(b）则可发现,据Davis、Wiegand[14]公式和模拟结果计算得到的环形空间内壁面Nu数随着Re数的增大也均呈现增大的趋势,但Davis公式与模拟结果的吻合度要略好于Wiegand公式。因此确定在分析环形空间内外壁面的对流换热时分别采用Davis公式和Dirker公式。

1.4 二氧化碳物性参数的确定

由于二氧化碳密度、黏度、热导率和热容等性质在流动过程中随温度和压力变化,二氧化碳的密度和热容采用Span-Wagner模型[16],而黏度和热导率的计算采用Vesovic[17]模型。

2 数值求解方法

由于连续管内、环空的温度和压力相互影响,总井段离散化过程中,不再分为连续管内和管外,而是沿着井深离散化为n个点,每一点同时具有4个主要参数：连续管内温度、环空温度、连续管内压力、环空压力。为使数值解稳定,使用交替方向迭代推进。即迭代分为向上、向下两个方向,分步计算连续管内与管外的温度,向下推进时,只计算连续管内的温度变化,向上推进时,计算环空温度变化,循环直至稳定。

将井筒长度自上向下以段长l分段,得到n个结点。每个节点包含4个未知量：连续管内温度Tp,环空温度Ta,连续管内压力pp,环空压力pa。初始计算时,已知连续管入口温度Tp(1）,压力pp(1）,未知出口环空温度Ta(1）,压力pa(1）,将预设的(Ta(1）, pa(1））(1）值代入,首先向下进行推进,各点参数计算公式为

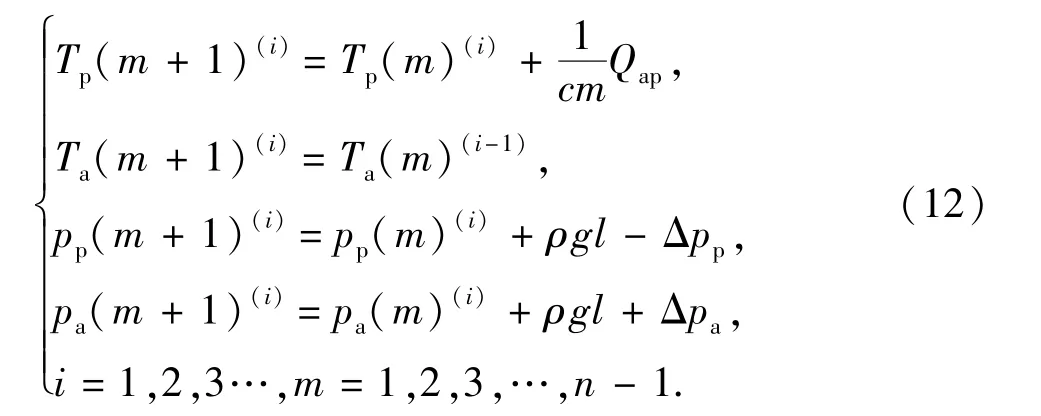
式中,i为迭代次数,m为节点序数。当迭代至最后一点,由于钻头存在压降和温降,第n点的参数应满足

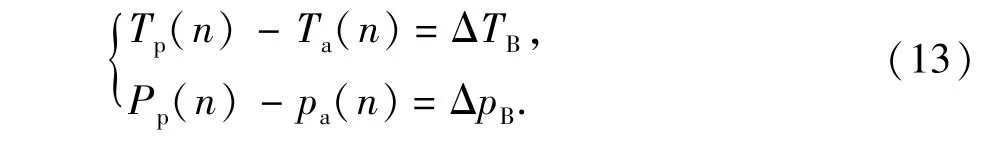
式中,ΔTB,ΔpB分别为钻头温降及钻头压降。实际计算中,最后一点迭代完成后,对其进行修正,即

即认为井筒内各点的温度和压力值收敛至稳定,其中Tc、pc为特征温度压力,采用二氧化碳的临界值进行计算。若

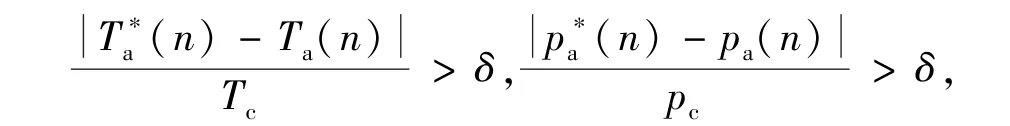
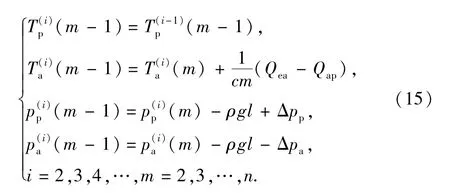
向上迭代完成后,重复进行正向推进,连续管入口温度压力仍为已知Tp(1）、pp(1）,环空出口温度和压力Ta(1）、pa(1）采用迭代得到的新值,继续循环直至满足收敛条件。

3 井筒内温度和压力分布规律分析

设定井深2.2 km,连续管下深2.2 km,套管下深2.1 km,连续管内径43 mm,外径50.8 mm,套管外径114.3 mm,内径101.6 mm,钻头喷嘴当量直径12 mm,喷嘴流量系数取为0.95,排量为3.78 L/s,二氧化碳井筒入口温度-20℃,地面环境温20℃,地层温度梯度2.8℃/(100 m）,二氧化碳泵入井筒压力13 MPa。依据所建立的传热模型,分析二氧化碳在连续管井筒内温度、压力、密度和相态随井深的变化情况,结果见图5～8。

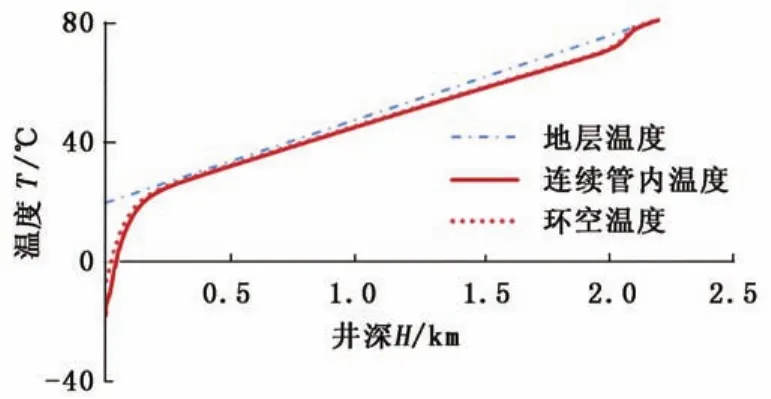
图5 二氧化碳在井筒内的温度变化Fig.5 In-tube and annular temperature profile in wellbore

由图5看出,连续管内二氧化碳温度随井深增大而迅速上升,本文条件下,在井深300 m左右即与地层温度接近,其后与地层温度一起随井深同步增大,在井筒下部裸眼段与地层温度最为接近。主要原因是二氧化碳在近井口段与地层之间的温差大,致使热流量高,传热速率快,其温度随着井深的增大与地层温度接近后,传热速率趋于稳定,而井筒裸眼段无套管与水泥环,热阻降低,传热效率增大,致使二氧化碳温度有小幅上升。二氧化碳在环空上返过程中,在相同井深,二氧化碳的温度略高于连续管内,其原因是二氧化碳在连续管内和环空中的流速较高,连续管壁厚较小,对流热传递及热传导的效率均较高,致使连续管内和环空中二氧化碳的温差较小。

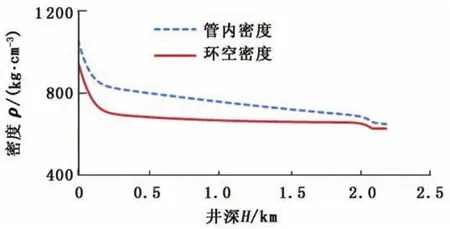
图6 二氧化碳在井筒内的密度变化Fig.6 In-tube and annular density profile in wellbore

由图6发现,二氧化碳密度在连续管内的井口处最高,其后随着井深的增大,二氧化碳密度先是急剧减小,到达一定井深后,减小幅度渐趋稳定,进入裸眼段后,减小幅度则略有增大。这主要是由连续管内二氧化碳的温度变化所致：在较浅的井深范围内随着井深的增大,二氧化碳在井筒内的温度迅速升高,导致其密度剧烈减小;当二氧化碳的温度随井深的增大趋于稳定后,其密度的变化也相应稳定;进入裸眼段后,因二氧化碳温度又有明显上升,致使其密度降低的幅度相应增大。在相同井深,环空中二氧化碳的密度明显小于连续管内的流速,这是因为二氧化碳在环形空间的流速小于连续管内,沿程压力损耗较低,致使流体密度降低。

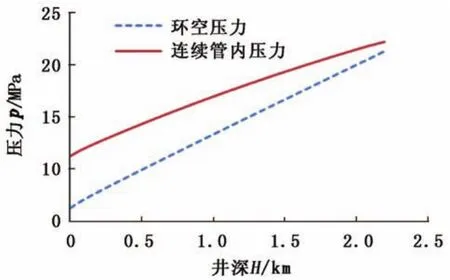
图7 二氧化碳在井筒内的压力变化Fig.7 In-tube and annular pressure profile in wellbore

由图7看出,连续管内压力随井深的增加而增大,但增幅则略显下降。这是由于随着井深增加,二氧化碳密度逐渐减小,致使连续管内液柱压力的增幅也相应减小。二氧化碳沿环空上返时,其压力不断降低,变化幅度较连续管内压力变化大;相同井深时,二氧化碳在环空中的压力则要小于连续管内的,其原因是环空中二氧化碳的密度要小于连续管内的密度。本文条件下,在出口节流阀管径为6.5 mm时,井口套压和钻头压降分别约为6.27和0.94 MPa。

由图8看出,本文条件下,进入井筒的液态二氧化碳在井深450 m处,其温度和压力均达到临界值,并随井深的增加持续增大,说明二氧化碳自井深450 m开始,在后续井筒内均保持为超临界态流动。在环空上返段,二氧化碳温度和压力开始降低。当低于临界值时,其相态则由超临界态转变为液态(井深也约为450 m处）,且随着井深减小,环空中压力进一步降低,二氧化碳逐渐过渡到气液两相,直至返出井口。

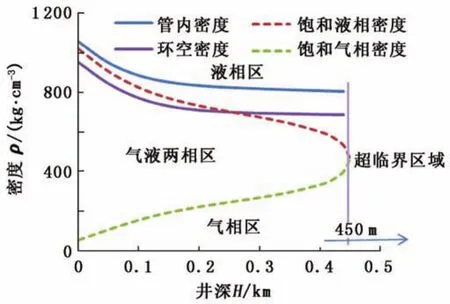
图8 二氧化碳在井筒内的相态变化Fig.8 Phase change of carbon dioxide in coiled tube

路易斯安那州立大学[2,18]采用44.5 mm连续管,套管直径为114.3 mm,井筒段为4 378 m,井口回压为5.5 MPa时,计算得到670 m井深时从液态转换为超临界态。基于相同条件,本文计算结果显示,二氧化碳在井深572 m时转变为超临界态。二者存在差异的主要原因是本文所建立的传热模型中考虑了井下温度和压力的变化对二氧化碳传热效率的影响,与真实工况更为接近。

4 结 论

(1）基于井筒流动过程中二氧化碳热力学性质及迁移性质的变化,考虑钻头处节流效应,采用数值模拟方法分析二氧化碳在环空内外侧的对流传热,筛选确定可用于分析连续管井筒传热问题的经验公式,建立二氧化碳连续管钻井井筒内热量传递基本模型。基于连续管内及环空中温度压力耦合,形成交替方向推进的求解算法。

(2）二氧化碳在连续管内流动时热交换效率较高,温度上升幅度随着井深的增大逐渐减小;而当它沿环空上返时,其温度逐渐降低,在靠近井口处温度显著下降。二氧化碳的密度明显受其温度和压力的影响。

(3）随着井深的增大,连续管内的液态二氧化碳逐渐转变为超临界态,沿环空上返过程则再次转变为液态,继而变为气液两相至出口。

[1] 陈会年,张国龙,胡清富.连续油管钻井技术的发展及应用[J].石油钻探技术,2000,128(2）：19-21.

CHEN Hui-nian,ZHANG Guo-long,HU Qing-fu.Developments and applications of coiled tubing drilling techniques[J].Petroleum Drilling Techniques,2000,128 (2）：19-21.

[2] AL-ADWANI F,LANGLINAIS J,HUGHES R.Modeling of an underbalanced-drilling operation using supercritical carbon dioxide[J].SPE Drilling and Completion, 2009,24(4）：599-610.

[3] 杜玉昆,王瑞和,倪红坚,等.超临界二氧化碳射流破岩试验[J].中国石油大学学报：自然科学版, 2012,36(4）：93-96.

DU Yu-kun,WANG Rui-he,NI Hong-jian,et al.Rockbreaking experiment with supercritical carbon dioxide jet [J].Journal of China University of Petroleum(Edition of Natural Science）,2012,36(4）：93-96.

[4] 王瑞和,霍洪俊,杜玉昆,等.超临界二氧化碳钻完井技术及风险分析[C]//中国职业安全健康协会2010年学术年会论文集.北京：煤炭工业出版社, 2010.

[5] RAMEY H J.Wellbore heat transmission[R].SPE 96, 1962.

[6] HOLMES C S,SWIFT S C.Calculation of circulating mud temperatures[J].Journal of Petroleum Technology, 1970,22(6）：670-674.

[7] KABIR C S,HASAN A R,KOUBA G E,et al.Determining circulating fluid temperature in drilling,workover, and well-control operations[J].SPE Drilling and Completion,1996,11(2）：74-79.

[8] GUPTA A.Feasibility of supercritical carbon dioxide as a drilling fluid for deep underbalanced drilling operations [D].Louisiana State：Louisana State University,2006.

[9] CHUNG S Y,SUNG H J.Direct numerical simulation of turbulent concentric annular pipe flow(2）：heat transfer [J].International Journal of Heat and Fluid Flow,2003, 24：399-411.

[10] MONRAD C C,PELTON J F.Heat transfer by convection in annular spaces[J].Trans AIChE,1942,593 (38）：123.

[11] DIRKER J,MEYER J P.Convective heat transfer coefficients in concentric annuli[J].Heat Transfer Engineering,2005,26(2）：38-44.

[12] STEIN R P,BEGELL W.Heat transfer to water in turbulent flow in internally heated annuli[J].AIChE Journal,1958,4(2）：127-131.

[13] MACADAMS W H,MCADAMS W H.Heat transmission[M].New York：McGraw-Hill,1954.

[14] WIEGAND J H,MCMILLEN E L,LARSON R E.Discussion on annular heat transfer coefficients for turbulent flow[J].AIChE J,1945,41：147-153.

[15] WILSON E E.A basis of rational design of heat transfer apparatus[J].ASME Journal of Heat Transfer,1915, 37：47-70.

[16] SPAN R,WAGNER W.A new equation of state for CO2covering the fluid region from the triple-point temperature to 1100 K at pressure up to 800 MPa[J].J Phys Chem Ref Data,1996,25(6）：1509-1596.

[17] VESOVIC A,WAKEHAM W A.The transport properties of carbon dioxide[J].J Phys Chem Ref Data, 1990,19(3）：763-808.

[18] GUPTA A,GUPTA A,LANGLINAIS J.Feasibility of supercritical carbon dioxide as a drilling fluid for deep underbalanced drilling operation[C].SPE Annual Technical Conference and Exhibition,2005.

(编辑 刘为清）

Wellbore heat transfer law of carbon dioxide coiled tubing drilling

WANG Rui-he,NI Hong-jian
(School of Petroleum Engineering in China University of Petroleum,Qingdao 266580,China）

Based on heat transfer process of carbon dioxide wellbore flow,the heat and pressure transfer mechanism of carbon dioxide in the wellbore,as well as the carbon dioxide property variation and phase change were investigated.The wellbore heat transfer model of carbon dioxide was developed,through which the wellbore temperature and pressure profiles were analyzed using alternate direction method.The results show that heat transfer efficiency is relatively high in wellbore.The increase extent of temperature for carbon dioxide reduces with the well depth gradually.Annular temperature of carbon dioxide decreases along the flow,and the temperature decreases significantly near the wellhead.The phase of carbon dioxide changes from liquid to supercritical state along the flow,then to liquid phase in the annular area.It changes to liquid-gas state at last.

carbon dioxide;coiled tube;wellbore heat transfer;pressure loss

TE 242

A

1673-5005(2013）05-0065-06

10.3969/j.issn.1673-5005.2013.05.009

2013-07-02

国家自然科学基金重点项目(51034007）;山东省自然科学基金重点项目(ZR2011EEZ003）;国家“973”计划项目(2010CB226703）

王瑞和(1957-）,男,教授,博士,博士生导师,主要从事高压水射流和油气井流体力学研究。E-mail：wangrh@upc.edu.cn。