基于排列组合熵的转子振动信号故障诊断SVM方法研究
2013-07-05赵凯李本威李冬李海宁
赵凯,李本威,李冬,李海宁
基于排列组合熵的转子振动信号故障诊断SVM方法研究
赵凯1,李本威1,李冬1,李海宁2
(1.海军航空工程学院飞行器工程系,山东烟台264001;2.大连理工大学船舶工程学院CAD工程中心,辽宁大连116024)
针对发动机转子的多种故障模式,提出了基于排列组合熵的SVM故障诊断方法。利用转子实验台,模拟了转子正常、转子不平衡、转子不对中、动静碰磨和基座松动5种典型振动模式,并使用振动传感器采集多路振动数据。计算振动数据的排列组合熵并将其作为故障特征向量,对特征向量样本集进行多级SVM分类诊断,并运用小波包能量特征提取方法提取信号特征。实例计算与结果对比表明,本文方法的正确率要高于基于小波包能量提取特征的SVM分类诊断方法,在提取转子振动信号的特征向量及在小样本下的故障分类诊断等方面,具有可行性和有效性。
发动机;转子振动;排列组合熵;特征提取;支持向量机
1 引言
转子是发动机的重要组成部件,在不同运行工况下会产生不同的振动信号。如何从杂乱无序的振动信号中提取有用信息,识别转子振动信号的不同模态,挖掘振动信号与故障模式之间的关系,对于发动机运行状态监测及故障诊断等有着重要的意义与价值。
排列组合熵(PE)[1]是一种描述时间序列复杂性测度的非线性动力学参数,其主要特点是计算速度快,容易编程,对噪声不敏感,只需要长度较短的时间序列就能计算出较稳定的特征值。近几年,基于排列组合熵的方法,已在心电信号分析[2]、脑电信号分析[3,4]、语音信号分析[5]、图像识别处理[6]等方面的研究中得到应用,但应用在发动机转子振动信号分析上的研究还很少。
相比之下,小波及小波包变换应用于振动信号分析的研究已为数不少[7~9],但其主要问题在于要确定小波(包)函数和分解层数等,分析得到的小波分量和小波谱只相对所选择的小波基有意义,不同的小波函数得到不同的结果。目前,大多通过实验结果对比验证取其优来解决。
本文运用排列组合熵算法,对转子振动信号的5种典型模式(转子正常、转子不平衡、转子不对中、动静碰磨和基座松动)进行研究。首先利用排列组合熵算法提取出用于故障检测的特征参数,然后使用多级支持向量机(SVM)进行分类诊断,最后对比研究小波包变换[7,9]提取信号特征的方法。希望本研究可为研究转子振动及发动机状态监控提供一些新的思路和方法。
2 理论基础
2.1排列组合熵
相比传统的信息熵计算方法,排列组合熵直接将时间序列{} xi作为有效熵源,而不是通过重构的时间序列来计算熵值。排列组合熵的具体定义[1]如下:
设有一维时间序列{} xtt=1,2,…,T,其长度为T。在
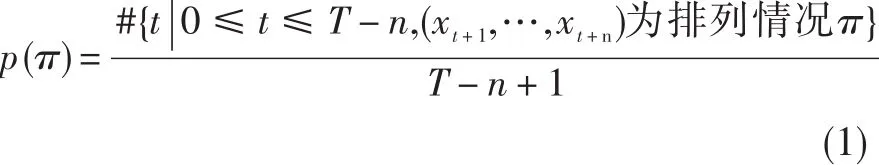
为准确计算p(π),须假定一组无限的时间序列{x1,x2,…},并按上述公式将T→∞取极限。当潜在随机过程满足一非常微弱的静止状态条件时,其极限值的概率为1;对于k≤n,xt<xt+k的概率不取决于t。当n≥2时,排列组合熵的定义为:
式中:H(n)为计算了按顺序排列的n个数的排列情况π的所有n!种情况之和。
排列组合熵的大小反应了时间序列的不规则程度,排列组合熵值越大,时间序列越不规则,值越小越规则。由排列组合熵的定义可看出:若时间序列有规则(如周期性),则其排列组合熵为0;若时间序列是白噪声随机的,则各种排列组合情况(共n!种)均以等概率出现,故其排列组合熵为log(n!)。因为时间序列大多随机或不具有完全的周期性,所以排列该时间序列中取n个不同的数,并将其尽可能按次序排列,排列顺序为π,是所有的n!种排列组合方式中的一种,即P1,P2,…,Pk,k≤n!。对于一有限时间序列,每种排列情况π的概率p(π)由其出现的相对频率确定,即组合熵的范围为0≤H(n)≤log(n!)。将排列组合熵进行归一化计算:

归一化计算将排列组合熵H(n)的值限定在[0,1],这样可更直观地观察与比较各时间序列的熵值。
2.2支持向量机
支持向量机(SVM)在解决小样本、非线性、高维模式识别问题中具有许多优势[10]。其主要思想是找到一个超平面,使得它能尽可能多地将两类数据点正确分开,同时使分开的两类数据点距离分类面最远[11]。
支持向量机方法用于解决两类分类的问题,而实际中故障诊断往往为多类分类问题,因此需要构造多类SVM分类器[12]。本文使用一对多的分类算法,该算法对样本数据可构造多个两类分类器,计算过程为:在构造第一个分类器时,将第一类训练样本作为一类,决策函数输出为+1;其它样本作为另一类,决策函数输出为-1。将第一类样本与其它样本区分开,然后对所有剩余样本数据进行分类,这样就构造出多类分类器。
本文基于排列组合熵的SVM故障诊断基本流程(图1)是:测得转子的振动数据,对振动数据的时间序列进行排列组合熵计算;将熵值作为特征向量建立样本集,对样本集进行多级SVM分类诊断。

图1 基于排列组合熵的SVM故障诊断流程图Fig.1 SVM fault diagnostic flow chart based on permutation entropy
3 实例计算与分析
利用YE6254型转子实验台(图2),对转子正常、转子不平衡、转子不对中、动静碰磨和基座松动5种典型振动模式进行模拟实验。4个振动传感器分别安装在实验台轴承两端的纵向和径向,这样每次实验可采集4路信号。转子转速在2 000 r/min时,采集以上5种类型的振动数据,每种采集40组,一共采集200组振动信号作为实验样本。采样频率为500 Hz,每组数据样本长度为2 000个点[9]。

图2 YE6254型转子实验台Fig.2 YE6254 type rotor test bed
3.1参数选取
将长度为T的振动信号时间序列划分为若干个长度为r的子序列,这些子序列间可重叠也可不重叠。本文选取子序列最大重叠序列,即子序列向后只移动一个时间点即得到下一个子序列,这样子序列个数为T-r+1。若要完全不重叠,子序列个数为[T/r]+1。显然,取最大重叠序列得到的信息量最多。
由文献[2]可知,r取值太小,计算结果不能完全提取序列的特征;r取值太大,结果又会失去精确性。对每个子序列进行排列组合熵计算,即每隔一个样点取连续的m个样点,对这m个样点进行升序排列,按式(2)计算得到排列组合熵,再按式(3)计算得到归一化的排列组合熵。将这T-r+1个熵值按时间排列就构成了长度为T的原振动信号。因此,如何选取r和m,是正确计算排列组合熵值的关键。
针对r和m的取值问题,文献[3]~[5]采用对比验证的方法选取最优解。这种方法依靠实验比较或操作人员的经验得到结论,主观性较强。Kim等针对非线性时间序列,提出了基于嵌入窗法思想的C-C方法,其特点是容易计算且计算量较小,适合小数据组计算[13,14],使用关联积分可同时估算出时延嵌入维数与嵌入窗。对本文使用的数据,经计算得出t= 1,m=5,r=200。
3.2实例验证计算
下面验证r和m的取值是否合适,所用数据为一组转子不平衡故障的振动信号。
图3给出了转子不平衡振动原始波形(按时间排列),及其不同子序列长度时的排列组合熵波形,m取值均为5。可见,r=190的波形相对于r=200的波形毛刺较多,有些部分没有完整提取子序列特征;r=210的波形相比之下熵值不够精确,提取的信息有部分丧失。所以取r=200较为合适。
图4给出了r=200,m分别取4、5、6时转子不平衡振动信号的排列组合熵波形。可见,m的取值基本上不影响排列组合熵随时间变化的波形,只是排列组合熵的值随m的增大而增大。这是因为:根据式(2),m越大,每m个样本点出现排列的方式就越多,即各个m对应的排列情况总数l=r-m+1分别为197、196、195,虽然每种排列情况出现的相对频率减小,但l在增大,m依次取4、5、6时计算得到各个熵值之和H(n)增大,因而排列组合熵的值越大。从图中可明显看出,m=4的波形相对于m=5的波形过于毛糙,而m=6的波形相比之下提取的信息有部分丧失,所以m取5较为合适。
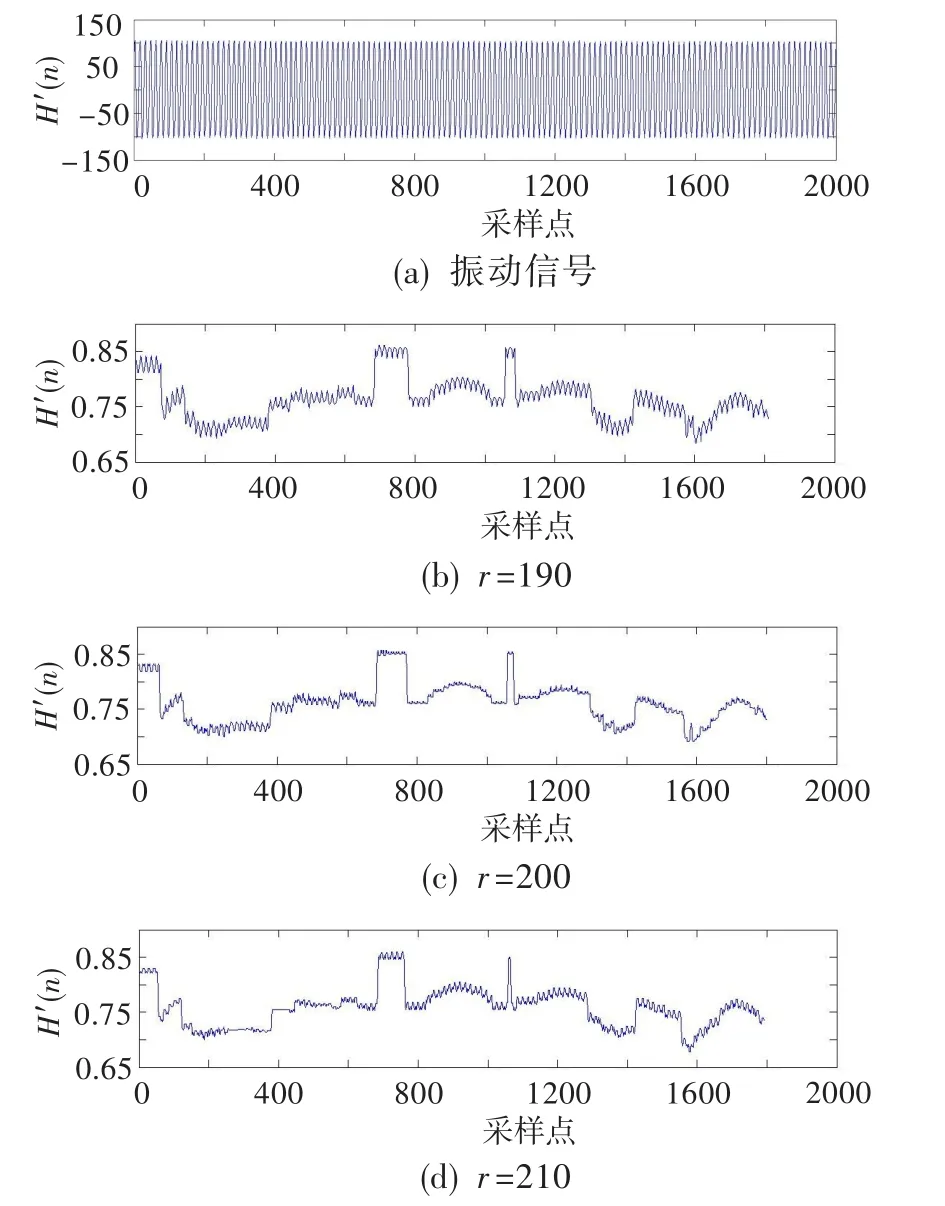
图3 转子不平衡振动数据及其不同子序列长度时的排列组合熵(m=5)Fig.3 Permutation entropy of rotor imbalance vibration data (m=5)
由此验证了C-C方法,即m=5、r=200合适。按式(2)计算5种振动信号的排列组合熵,共200组数据,并将其归一化计算,然后按次序排列,结果如图5所示。可见,不同类型转子振动信号的排列组合熵值分布在不同区间,且转子正常振动信号对应的熵值最小。因为当转子在平衡状态运转时,振动信号的时间序列没有变化,因此排列组合熵值很小,由前文可知其理论值应为0;当转子出现故障时,振动信号丧失周期性,排列组合熵增大。图中,基座松动故障的排列组合熵最大,这是由于基座松动的振动信号杂乱无章且随机,故而其熵值接近1。
3.3基于SVM的转子振动故障诊断与分析
建立支持向量机的特征样本集作为SVM的输入向量。首先将每一次采集的4路振动信号分别进行排列组合熵计算,然后将其组成一组4维特征向量组,将此特征向量组作为转子振动状态的一个样本,最后所有的排列组合熵特征向量的集合就构成了特征向量集。将其中10组作为训练样本集,其余作为测试样本集。

图4 连续样点数不同时转子不平衡振动数据的排列组合熵(r=200)Fig.4 Permutation entropy of the rotor imbalance vibration data (r=200)
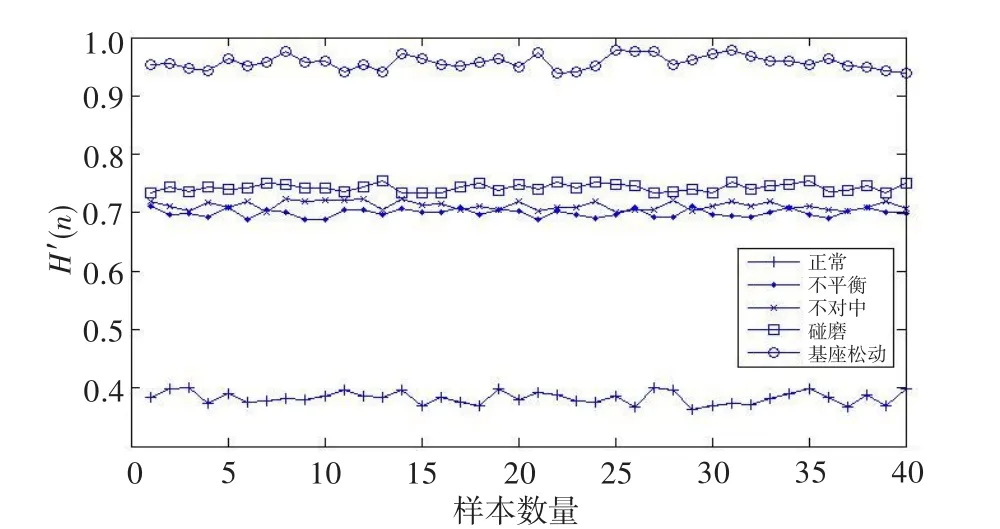
图5 各故障模式对应的排列组合熵数据图Fig.5 Each failure mode corresponding to the permutation entropy data chart
本文实验有5种类型的转子振动信号,所以建立4个两类分类支持向量分类机。按图6所示的多级SVM分类流程建立多分类支持向量机,来识别这5种转子振动类型。SVM1表示将转子正常振动信号与其它类型故障进行分类,SVM2表示将不平衡状态与其它类型故障进行分类,SVM3表示将不对中故障与其它类型故障进行分类,SVM4表示将碰磨故障与基座松动故障进行分类,f(x)表示SVM的最优分类函数且

式中:sgn为符号函数,K(ai,x)为核函数。
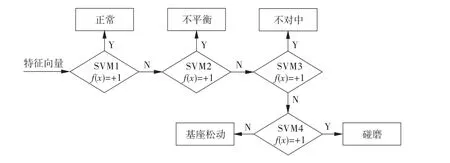
图6 多级SVM分类流程图Fig.6 Multi-class SVM classification flow chart
用支持向量机进行分类时,需确定核函数。SVM中主要的核函数有线性核函数、多项式核函数、径向基核函数、S形内核函数、傅里叶核函数等[11],本文选用具有良好分类和学习能力的径向基核函数:
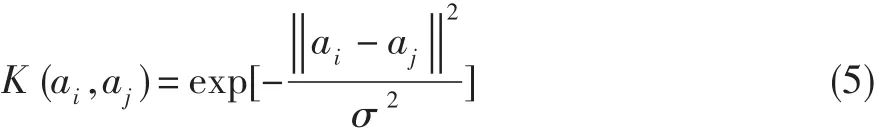
将样本集中各类转子振动信号的10个样本作为训练样本进行SVM训练。用训练后的支持向量机诊断模型对5种类型的样本进行分类测试,结果显示其正确分类率为100%,这说明该模型有很好的学习能力。然后用每种振动信号剩余的30个样本进行测试,结果表明该模型不但具有很好的学习能力,也具有不错的泛化和容错能力,可以对这5种振动信号进行有效分类。测试结果如表1所示。
3.4小波包分析对比研究
将本文方法与文献[9]中使用的小波包方法进行对比研究。对这5类振动信号200组数据分别进行小波包变换。选择sym10小波基,对数据进行5级小波包分解。对分解所得的8个频段信号的小波系数d(5,0)、d(5,1)、d(5,2)、d(5,3)、d(4,2)、d(4,3)、d(2,1)、d(1,1)进行频带划分,频带范围为0~500 Hz。对倍频进行4尺度分解,对基频进行5尺度分解,充分利用小波包的特性对感兴趣的频率成分进行细致划分。用各小波系数的平方来计算小波包分解各子频带上的平均能量,并对其归一化处理。表2示出了转子不平衡信号各频段小波分解系数对应的频带和归一化能量。
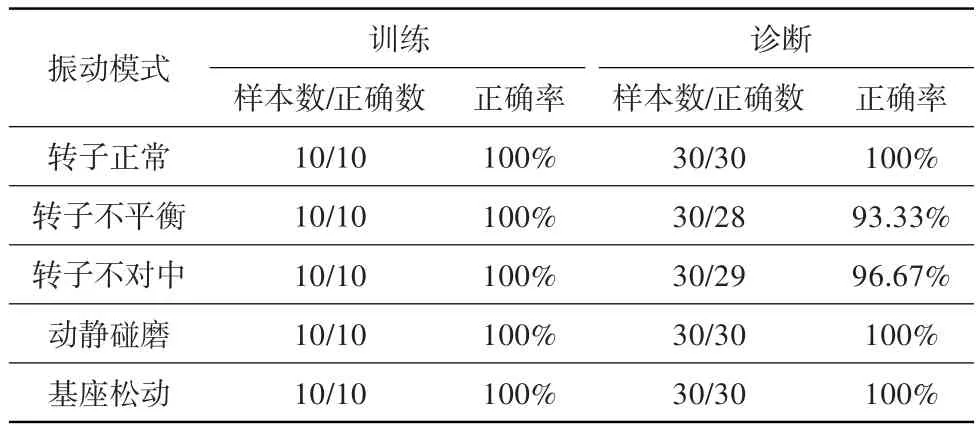
表1 基于排列组合熵的转子振动信号SVM诊断Table 1 SVM diagnosis of rotor vibration signals based on PE

表2 转子不平衡振动数据各频段小波系数对应的频带和归一化能量Table 2 Frequency bands and unitary energy for each frequency range wavelet coefficients of rotor imbalance vibration data
将此归一化能量作为一组8维的特征向量。同理,得到包含200组特性向量的样本集,作为SVM的训练与测试样本。同样将10组样本作为测试样本集,剩余30组作为诊断样本集,诊断结果见表3。可见,基于小波包能量算法的转子振动信号SVM诊断也具有较高的正确率,但总体上低于本文基于排列组合熵算法的SVM诊断正确率。另外,本文使用的排列组合熵算法简单,容易编程,且没有小波变换面临的一些不确定问题,即面对不同数据,选择不同小波基及分解层数等得到的结果不同。

表3 基于小波包能量的转子振动模式SVM诊断Table 3 SVM diagnosis of rotor vibration signals based on wavelet packet energy
4 结论
本文针对转子振动的5种典型模式,提出了基于排列组合熵的SVM故障诊断方法,即利用排列组合熵方法提取振动信号的特征值,然后对其进行SVM分类,得到诊断结果。文中还对比了小波包提取振动数据能量特征进行SVM诊断的方法,结果表明,本文提出的方法更适合区分转子的各种振动状态,且编程容易,效果较好。但也应该看到,本文仅研究了转子振动中的单故障现象,试验样本数据有限,并且是对实际发动机转子的理想简化,因此对实际发动机转子故障诊断的效果还有待进一步检验。
[1]Bandt C,Pompe B.Permutation Entropy–A Natural Com⁃plexity Measure for Time Series[J].Physical Review Let⁃ters,2002,88:1595—1602.
[2]赵小磊,任明荣,张亚庭,等.基于排列熵的心电信号非线性分析[J].现代电子技术,2010,33(19):90—93.
[3]范影乐,李谷,刘亚景,等.基于排列组合熵的脑电意识任务识别方法的研究[J].传感技术学报,2008,21(1):74—78.
[4]李谷,范影乐,庞全.基于排列组合熵的脑电信号睡眠分期研究[J].生物医学工程学杂志,2009,26(4):869—872.
[5]吴秀良,范影乐,钱诚,等.基于排列组合熵的语音端点检测技术研究[J].计算机工程与应用,2008,44(1):240—242.
[6]罗元俊,叶雪梅,范青刚.离散傅里叶变换和组合能量熵的纹理图像分析[J].电子科技,2011,24(1):9—11.
[7]艾延廷,费成巍.转子振动故障的小波能谱熵SVM诊断方法[J].航空动力学报,2011,26(8):1830—1835.
[8]艾延廷,费成巍.基于支持向量机的转子振动故障融合诊断技术[J].沈阳工业大学学报,2010,32(5):526—530.
[9]赵凯,孙涛,宋伟健.基于小波包分析的转子振动信号故障特征提取研究[J].海军航空工程学院学报,2009,24(6):613—616.
[10]吴虎胜,吕建新,来凌红,等.基于EMD-SVD模型和SVM滚动轴承故障模式识别[J].噪声与振动控制,2011,31(2):89—93.
[11]司守奎,孙玺菁.数学建模算法与应用[M].北京:国防工业出版社,2011:178—185.
[12]来凌红,吴虎胜,吕建新,等.基于EMD和样本熵的滚动轴承故障SVM识别[J].煤矿机械,2011,32(1):249—252.
[13]Kim H S,Eykholt R,Salas J D.Nonlinear Dynamics,De⁃layTimesandEmbeddingWindows[J].PhysicaD (S0167-2789),1999,127:48—60.
[14]陆振波,蔡志明,姜可宇.基于改进的C-C方法的相空间重构参数选择[J].系统仿真学报,2007,19(11):2527—2538.
SVM Research on Rotor Vibration Signal Fault Diagnosis Based on Permutation Entropy
ZHAO Kai1,LI Ben-wei1,LI Dong1,LI Hai-ning2
(1.Department of Airborne Vehicle Engineering,NAAU,Yantai 264001,China;2.Dalian University of Technology,Institute of Marine Engineering,CAD Engineering Center,Dalian 116024,China)
For a variety of rotor failure modes,the SVM fault diagnosis method based on permutation entro⁃py was proposed.Five kinds of typical faults:normal rotor vibration,rotor unbalance,rotor misalignment, rubbing and base loosening were simulated and vibration failure data was collected in rotor experiments. The permutation entropy of vibration fault signal was calculated as the fault feature,multi-class SVM was used to classify and diagnose the feature vector sample sets,signal feature was extracted by wavelet energy feature extraction.By calculating and comparing,the accuracy rate of the method in this paper is higher than the SVM method based on the wavelet energy feature extraction,and the fault diagnosis method was verified to solve the rotor vibration faults signal feature extraction and small sample cases validly.
engine;rotor vibration;permutation entropy;feature extraction;support vector machine
V235.13
A
1672-2620(2013)03-0038-05
2012-09-17;
2013-03-28
赵凯(1983-),男,山东烟台人,博士,研究方向为发动机测试理论与技术。
