改进的进化算法于服务机器人仿真赛中的应用

李剑平，陈 玮，陈树斌

（广东工业大学 自动化学院，广东 广州 510006）

0 引 言

家庭服务机器人仿真比赛立足于探索服务机器人的高层功能的，目前主要包括人机对话、自动规划和推理等。将服务机器人实体抽象为3D 仿真机器人，并通过建立仿真的室内环境为测试环境，将人机交流抽象为自然语言或命令语言表达的任务描述，将机器人对环境的感知数据抽象为文件格式的场景描述，从而便于研究服务机器人的高层功能［1］。在比赛当中要求求解程序对比赛平台提出的问题，根据其场景描述、任务描述、补充信息、约束信息等，在规定时间内自动规划生成完成该任务的原子行动序列，比赛平台将根据这些行动序列的性能给求解程序打分［2］。

在家庭服务机器人仿真比赛中，每次任务会有多个目标，机器人通过达到各个目标来达到服务效果，从而获得比赛的分数。而完成同样的任务可以有多种的方式，完成的顺序不限，且可以在完成一个目标的过程中穿插完成其他目标。所以这就对机器人的规划提出了要求，即如何用最少的动作，最简洁的方式来完成任务，从而让服务机器人的服务更加智能化，进而在比赛中取得更高的分数。

各参赛队伍的规划方式有很多种，如A＊算法、ASP回答集编程、贪心算法等等。这些算法各有优劣，A＊算法基于整个场景的状态转换计算，计算速度良好、可以得到较优的规划，但其占用系统资源多，且不能良好地处理物品选择问题；ASP 回答集编程利用穷举法并加以筛选，规划较为完善，但处理较长的任务时计算时间过长，有时不能在比赛规定时间范围内完成规划；贪心算法虽然计算速度快，但容易陷入局部最优值，不能得到全局最优解，规划效果差。

1 进化算法

1.1 进化算法简介

进化算法（evolutionary algorithm，EA）是一类随机优化算法，其中包括遗传算法（GA）、进化策略（ES）和进化规划（EP）等。它们利用某些启发式规则进行优化，其思想根源来自于进化论［3］。国内外许多大学及科研机构的研究人员正在努力从事这方面的研究，而对进化算法的改进也层出不穷，如混合混沌进化算法［4］、动态位置可变进化算法［5］、多智能体混合进化算法［6］等等。

1.2 进化算法一般步骤

（1）进行编码，将待解决的问题转化为进化算法便于计算的形式；

（2）产生初始种群；

（3）进行交叉、变异等计算产生新的个体；

（4）使用适应度函数对种群内的个体进行评价；

（5）选择种群中优化程度更高的个体作为新一代种群；

（6）若未达到稳定的最优解则返回第三步再次进化；

（7）得到最优解后解码输出结果。

1.3 新结构建立的必要性

为了使家庭服务机器人的规划问题转化为便于进化算法的计算，需要找到一个合适的结构作来描述机器人的任务，从而以之作为基础进行规划。

在家庭服务机器人仿真比赛中，任务的目标多种多样，为达到目标所需做出的动作也有很多的变化，下面给出某一个任务的例子和可能用来完成任务的一种方法，见表1。

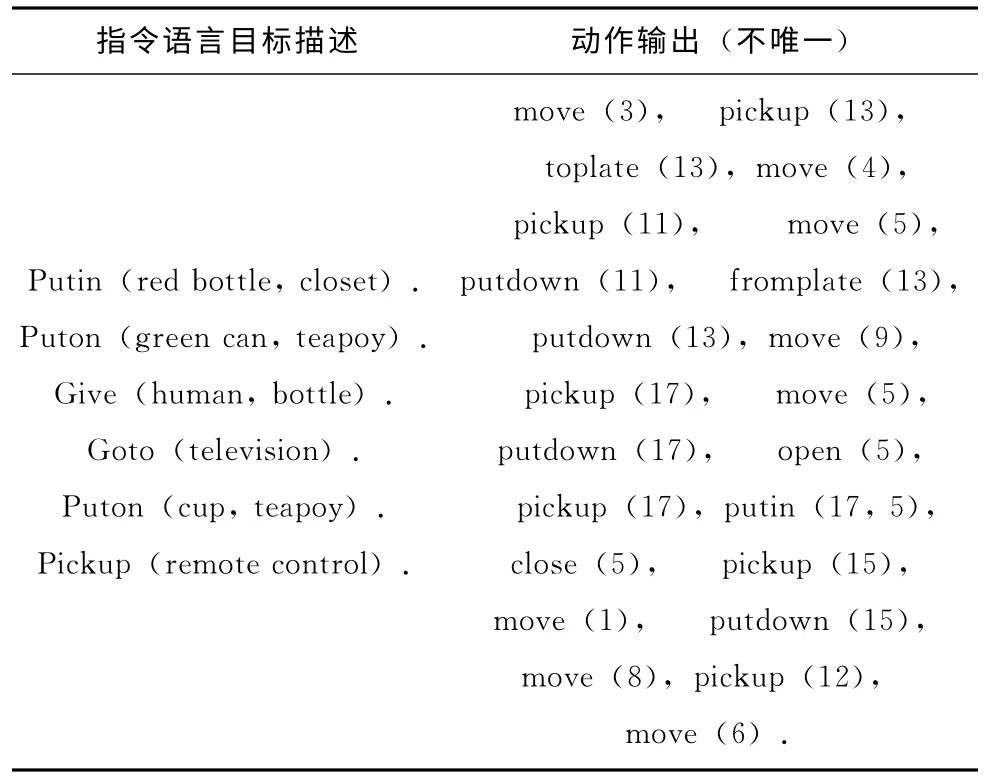
表1 机器人规划范例

例中目标数量为6，若以目标为规划基础，对其进行排序规划，其情况种类较少，且不能在完成某个目标过程中穿插完成其他目标，因而规划效果不佳。而动作输出的条数和内容都不定，且动作较多，计算复杂度高，也不适合作为规划的基础。

可见，基于目标的规划或者基于动作的规划效果和效率不会很高，因此本文将引入一个介于两者之间的新的结构，作为规划的基础。这个结构需要达到归一化的效果，并能完整地表示任务中的信息，且有一定的操作空间，便于对其进行评价，适合以进化算法进行优化，最终还能方便地解析成动作序列。

2 算法的改进

本文利用传统的进化算法进行改进，根据比赛需求建立新的编码方式，采用独特的交叉变异方法，使其在家庭服务机器人的行动规划中发挥效用。

2.1 事件结构与编码

本文把所有类型的目标都转化为若干个四位结构，称为事件或step。其结构如下：

step（getorput，objnum，objplace，inornot）

其中：getorput表示事件类型是一个拿取或放下小物体、又或与小物体无关的事件。

objnum 表示事件中涉及小物体的编号。

placenum 表示事件中涉及地点（大物体）的编号。

inornot表示是否存在一些内部包含的状态。

而编码即是把任务目标转化为这种事件结构，例如：Puton（green can，teapoy）.其中green can的编号为17，初始位置为3，且在大物体内部，teapoy位置为7的话。那么其即可转化为两条事件结构即step0（getorput＝1，objnum＝17，placenum＝3，inornot＝1），step1（getorput＝－1，objnum＝17，placenum＝7，inornot＝0）.其他目标也可依照类似规则转化为事件结构，于是规划问题转化为对事件结构的排序问题。

2.2 生成初始种群

传统进化算法的初始种群产生方法为随机产生，但这样并不能保证全面性，特别是在家庭服务机器人仿真比赛中，需要规划的参数较多，不仅是事件结构的顺序，物品选择方面也需要利用进化算法进行规划，所以尽量在初始种群保持一定的全面性。

因此，本文采用了条件随机生成的方式。在每种可能的物品选择情况下，随机产生若干个初始个体，个体内的事件结构随机排序，并经过序列筛选（见2.4.1）作为进化算法的初始种群μ。

2.3 交叉与变异

交叉和变异是进化算法中种群进化的重要方式，通过交叉、变异计算，产生新的种群，从而丰富种群的多样性，探索更优化的策略。通常进化算法中的交叉操作，是随机取两个染色体进行单点交叉操作［7］，而变异操作是指对个体编码串随机指定某一位或某几位基因作变异运算［8］。

2.3.1 交叉进化

为了解决排序问题，本文把传统的异体同位交叉转化成为自体异位交叉的模式，即在进行交叉进化时，个体中的任意m个事件对以交叉概率p进行位置互换，从而产生新的个体。其中交叉事件对个数m和交叉概率p与当前个体的适应度有关。即

式中：p——单对事件发生交叉的概率；μ——交叉率，取值和进化速度及稳定性有关；S——该个体的代价值；n——一个个体中事件的个数。

图1 交叉进化图例

发生交叉进化的概率p 与交叉率μ和代价值S 正相关，与事件个数n 负相关。由于代价值S 与优化程度负相关，即代价值S 越小则说明该个体的优化程度越高，需要发生交叉的概率则越小，反之亦然。而代价值S的计算与事件个数n 有关，因而加入n 以消除事件数量对交叉发生概率的影响。交叉率μ的值越大则进化速度越快，同时稳定性降低，反之则进化速度降低，但稳定性增强，需根据情况进行选择。

2.3.2 变异进化

物品选择是机器人规划中十分重要的一点，也是家庭服务机器人仿真比赛中必须考虑的部分。利用进化算法的变异进化可以有效地解决物品选择的问题，当然也需要对其进行一定程度的改变。

由于是用于物品选择，所以变异的参数以objnum为线索，其变异的范围也是限定的，为可以完成目标的同类物品，其发生变异的概率为q。当某条事件的objnum 改变时，该事件内的placenum和inornot 也依照情况根据小物体的状况而变化。且当仍有其他事件涉及同样的小物体时，该事件的小物体也随之而改变，即相当于一种成对变异的效果

式中：q——单个事件发生变异的概率；θ——变异率，取值和进化速度及稳定性有关；k［t］——目标小物体的可选择个数；S——该个体的代价值；n——一个个体中事件的个数。

图2 变异进化图例

在公式中，θ、S、n的意义和选择与交叉进化时相似，而k［t］则表示了该事件所用来完成的目标涉及的小物体的可选择数量。当可选择数量越多时，即k［t］越大时，需对变异进化进行促进，因而q越大，反之亦然。

由于交叉进化有可能会产生不能正确完成任务的事件序列，这部分序列会在序列的筛选中被删除，因而要产生较多的下一代种群以备选择，需要进行两次独立的进化产生2μ个子代种群，则整体种群数量变为3μ。

2.4 适应度函数与选择

适应度函数是进化算法非常重要的组成部分，整个进化算法就是在适应度函数的引导下进行的，适应度函数对个体的评价直接影响了选择，从而决定了整个群体的进化方向［9］。

2.4.1 序列的筛选

由于机器人的能力限制，以及一些动作之间固有的逻辑关系，通过随机生成或经过进化的事件序列并不都是合法的，其中很大一部分会与规则或逻辑冲突。这部分序列是不能正确地完成任务的，对其进行适应度评价也毫无意义，因而要在评价前将其从种群中移除。

如：规则规定机器人同时只能携带两个或两个以下的小物体，因而违反此规定的事件序列视为违规，应予以删除；当事件序列中涉及对同一物体的拿取事件和放下事件时，逻辑上拿取事件必须出现在放下事件之前，否则视为不合逻辑，应予以删除。以及诸如此类其他违反规则或逻辑的事件序列都删除处理，并且每次进化一代之后都进行一次序列的筛选。

2.4.2 适应度函数

本方法适应度函数采取代价累加的方式计算，根据事件结构的内容、机器人的状态、场景状态、需要维持的约束等等，结合类似罚函数的方法，计算出完成任务所需付出的代价（S）［10］。计算得出的代价值越高，则说明适应度越低，相反代价值越低，说明适应度越高。代价值计算具体公式如下

其中：S为该序列的代价值；

n为该序列包含的事件个数；

m、a、c为移动、动作、约束的代价权值；

x为特殊情况代价变化。

公式中的m、a、c权值是根据比赛规则对移动、动作、约束的评分系统而设定的，分别设为3、1、5。αi表示该事件是否有进行移动的需求，其为0或1二值，与机器人的当前位置和事件发生地点有关；βi 表示为完成该事件所需做出动作的复杂度，与事件的内容、机器人的状态、环境状态有关，是强非线性的映射关系；γi表示本次事件违反约束的量，需要根据事件本身的内容和约束列表得出。变量x为某些特殊情况对整体代价值的影响，例如事件结束时机器人状态刚好位于goto任务目标地点等等。

由此方法计算出的代价值与适应度成负相关，相关使用和操作也与适应度相反。

2.5 种群的选择

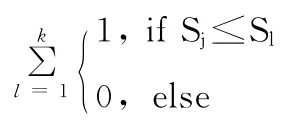
依照此规则对种群中每个个体进行计算以测试新种群，选择其中w 值最高的μ个个体作为下一代的初始种群。

2.6 终止条件与解码

本算法利用代价计算函数作为终止条件，当连续三代种群最低代价相同时，即视为达到相对最优解，随即终止进化，当前种群中的最佳个体作为规划结果。

当进化过程结束，选出了相对最优解之后，即进入解码过程。将排好序的事件结构结合机器人状态、场景状态等，转化成机器人最终执行的动作序列，见表2。

表2 解码范例

至此，整个机器人规划过程结束。

3 实验与结果

实验素材为2011中国服务机器人大赛指令语言仿真组和自然语言仿真组比赛用题，每组包含两个阶段（stage），每个阶段50个任务，每个任务包含若干个目标和约束等，算法应用于我校GDUT＿TiJi队，并取8个其他学校参赛队为参照系，各参赛队采用A＊算法、ASP 回答集编程等完全独立的方法。其中stage1只包含目标，而stage2包含目标及约束，更为复杂，对规划的要求更高。实验结果包含整组题目的对照情况，以及对具体单个题目比较的统计数据。

表3中score为各队单个阶段得分，higher为该队单题得分超过我队的题目数，lower为该队单题得分低于我队的题目数，different为单个阶段得分差，rank为该队在比赛中的排名。

由实验结果可以看出，该结构算法在家庭服务机器人仿真比赛中应用良好，得分高于其他队的题目很多，而得分低于其他队的题目则相对较少，且在状况更复杂的第二阶段能取得更好的成绩，成功达到规划效果。使用这个方法，我校GDUT＿TiJi队在2012中国服务机器人大赛中取得了指令语言组季军、自然语言组亚军的成绩，再一次证明了这个方法的实用性。

4 结束语

本方法提出了事件结构描述家庭服务机器人的任务，构建了一种代价函数还对机器人的行动进行评价，且改进了进化算法的进化方式以适应这种事件结构。并通过实验和比赛也验证了这个方法的稳定性和有效性。

其算法还有很多方面有待进一步探讨，比如事件结构的细化优化、参数的选取、加入启发式搜索方法等等，需要在今后的研究中继续探索。

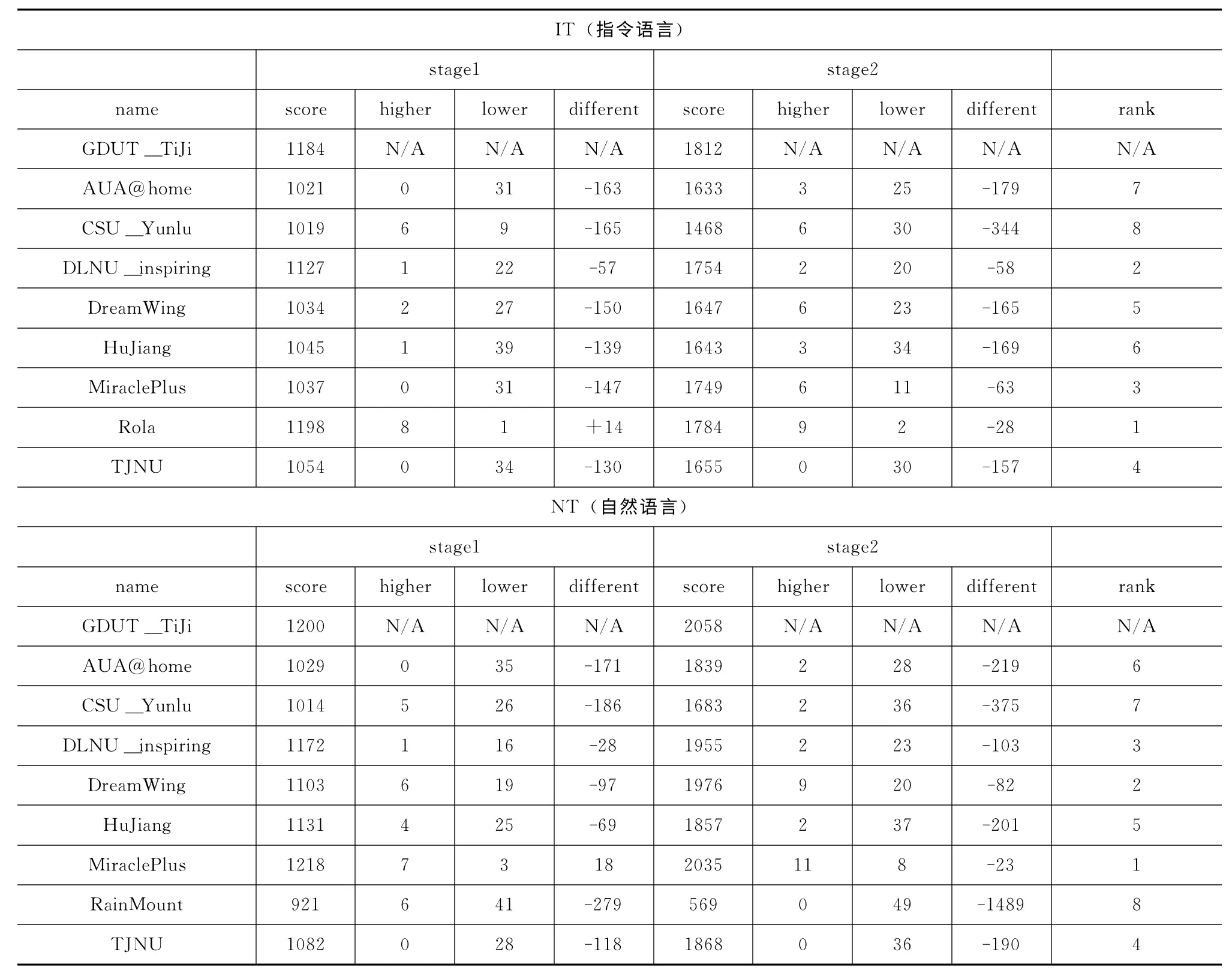
表3 实验结果

［1］RoboCup＠home Rule 2011［Z］.2011（in Chinese）.［2011中国服务机器人大赛仿真比赛规则［Z］.2011.］

［2］JI Jianmin.Several ways of improve the ASP efficiency and application on service robot［D］.Hefei：University of Science and Technology of China，2010（in Chinese）.［吉建民.提高ASP效率的若干途径及服务机器人上应用［D］.合肥：中国科学技术大学，2010.］

［3］HUANG Han，LIN Zhiyong.Convergence analysis and comparison of evolutionary algorithms based on relation model［J］.Chinese Journal of Computers，2011，34（5）：801－811（in Chinese）.［黄翰，林智勇.基于关系模型的进化算法收敛性分析与对比［J］.计算机学报，2011，34（5）：801－811.］

［4］HAO C Y M Z C.A hybrid chaotic quantum evolutionary algorithm［J］.Intelligent Computing and Intelligent Systems，2010：771－776.

［5］Woldesenbet Y G Y G G.Dynamic evolutionary algorithm with variable relocation［J］.Evolutionary Computation，2009.13（3）：500－513.

［6］ZHENG X G J.Multi－agent based hybrid evolutionary algorithm［J］.Natural Computation，2011（2）：1106－1110.

［7］DENG Zexi，CAO Dunqian.New differential evolution algorithm［J］.Computer Engineering and Applications，2008，44（24）：40－42（in Chinese）.［邓泽喜，曹敦虔.一种新的差分进化算法［J］.计算机工程与应用，2008，44（24）：40－42.］

［8］WANG Shuaiqiang.A novel method for behavioral model refinement and learning to rank based on evolutionary algorithm［D］.Jinan：Shandong University，2009（in Chinese）.［王帅强.基于进化计算的行为模型自动精化和排序学习方法的研究［D］.济南：山东大学，2009.］

［9］Majig M A，Fukushima M.Adaptive fitness function for evolutionary algorithm and its applications［C］／／International Conference on Informatics Education and Research for Knowledge－Circulating Society，2008：119－124.

［10］LIU Bo，WANG Ling.Advances in differential evolution［J］.Control and Decision，2007，22（7）：721－729（in Chinese）.［刘波，王凌.差分进化算法研究进展［J］.控制与决策，2007，22（7）：721－729.］