改进的遗传算法优化二维不规则图形排样

卢齐飞，唐 平，张光富，包梦华

（广东工业大学 自动化学院，广东 广州 510006）

0 引 言

二维不规则排样问题是指将一系列二维平面图形（或零件）互不交叠地放置在某一板材上，使得未被覆盖的面板面积最小，并且使零件在板材上的排布最优，使得板材的利用率最大。相比于矩形件排样，不规则排样的零件和板材为任意多边形，板材还可能包含内部孔洞，并且增加了排样角度。从计算复杂性理论来看，二维不规则排料问题属于具有高计算复杂性的NPC问题。

为此，国内外众学者提出了很多不同的排样优化算法。文献［1］提出了一种分层双螺旋染色体结构的遗传算法来解决排样问题。在排样策略上对种群重组和保持种群的多样性提供了新思路，但是文中并没有考虑多边形旋转的问题。文献［2］提出了一种基于离散差分进化算法的新方法，它将板材排样问题分解成多个单层的排样问题，再将单层堆叠组合成包，能够很好地解决板材中产生的空隙问题，但是该方法还处于实验阶段。文献［3］设计了基于邻域搜索和遗传算法的混合算法，这种算法既发挥了遗传算法的全局搜索能力，又体现了邻域搜索算法的局部搜索能力，但是文献中只做了矩形件的实验，对于不规则图形的排样，算法效率不得而知。文献［4］提出了一种基于重心NFP的二维不规则多边形排样算法，该算法可以处理板材和零件均为不规则形状的排样问题，但是算法时间复杂度太高。文献［5］利用图形间的相似度对待排样的图形进行分类，从而达到降低算法时间复杂度的目的，但是文献中对相似度的计算规则比较模糊，很难判定两个图形怎样才算相似以及相似程度多少等问题。上述工作主要从改进算法和改进排样策略这两个方面着手，以期达到提高排样效率的目的。但是对于问题规模较大时，零件的形状并不规则时，计算时间较长，排样的利用率不高。

因为石材大板具有不规则廓形和各种表面缺陷，所以石材的排样是二维不规则排样问题。本文针对石材排样的特点对它进行了算法设计。首先在算法步骤上进行改进，在编码方式上采用二进制与十进制编码相结合的方法，编码串太长问题和有些相近编码方案获得的材料利用率相去甚远问题得到了一定程度上的解决。然后在排样策略上，提出了基于图形矢量信息的相似度的明确计算方法，降低了算法的时间复杂度。并利用该算法，对算例进行测试。从实验数据结果来看，排样质量和排放速度都有提高。

1 问题描述

多边形的排样问题就是将n个大小不一的多边形放在一块宽为W，长为L的板材中，并寻求一种最佳的排放次序使得该板材的利用率最大。因为多边形各个顶点的位置关系我们已经知道，所以只需已知它其中一个顶点的坐标（x，y）和旋转角度α，那么就可以对它进行定位。设Zi（i∈I，I为多边形集合）为第i个多边形，Si为第i个多边形的面积，H为所有多边形排放后总的结果高度，Emax为最大板材利用率，Zig为图形i的第g个顶点的坐标，α为图形i的旋转角度，Zjg为图形j的第g个顶点的坐标，β为图形j的旋转角度，其中g 表示两个图形中的任意一个顶点。为了达到板材利用率最大的目标Emax，其中Emax可以用式（1）表示

必须满足下列约束条件：

（1）Zi和Zj不能重叠，即当i≠j时，满足式（2）的条件

（2）Zi必须在板材内，而且必须有一部分图形与板材的边界接触，则肯定要满足条件：

k为有k个图形，m为第k个图形的第m个顶点。

（3）多边形的最初排放符合BLF原则。

（4）按面积从大到小的顺序排放，并且同种多边形尽量排布在一起。

（5）先把有瑕疵的石材区域包络成最接近区域大小的矩形，并把此区域记作Bi，i∈（1，2，…，m），m为有m个瑕疵区域。要求待排样的多边形与包络区域不相交，即要求满足式（4）

2 改进的优化排样智能算法

经典的遗传算法优化排样问题是一个多参数优化问题，它对图形进行编码排序产生初始种群，然后通过交叉，变异等一系列遗传操作，得到不同的排列顺序，并挑选出这一代中最优的，能够使板材利用率最大的排列序列，把它保存起来，随后进行迭代比较，直至经过一定的迭代次数得到最优或次优解。而本文提出的算法为了解决随着种群规模的增大，传统算法的复杂度也相应呈指数增大的问题，对经典方法进行了改进。本文算法优化排样的主要操作有：

2.1 图形预处理

因为要排样的图形包括了矩形，三角形，梯形，平行四边形和不规则图形，所以我们可以先把前面几种规则图形排在一起。例如，可以把三角形对排在一起，变成平行四边形之后，再进行排放；两个梯形也可以按照上述方法组合成一个平行四边形，然后把组合后的平行四边形与原有的平行四边形联排。对于不规则件，先获取不规则零件内、外轮廓信息，板材信息，先设定一个最小矩形包络率，判断零件是否大于最小矩形包络率，如果是的话，则对零件进行包络；如果否，则判断零件是否大于相似度阈值。如果大于则进行相似度计算，如果都不满足，则进行后续操作。

图形的拼接与碰靠如图1所示。

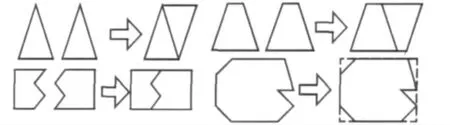
图1 图形的拼接与碰靠

2.2 混合编码表示

编码是应用遗传算法时要解决的首要问题，也是设计遗传算法时的一个关键步骤，它除了决定了个体的染色体排列形式之外，还决定了个体从搜索空间的基因型变换到解空间的表现型的解码方法。一般编码表示有二进制编码，十进制编码和格雷码，但是格雷码并不适用于排样问题，而经典的遗传算法通常采用二进制编码或者十进制编码。然而Holland证明：当使用二进制编码时，个体中包含的模式数目最多，所以他建议使用二进制串来表示个体。但是最大的内在并行性并不能保证提供最优的性能，二值串的使用并没有得到普遍赞同。实际上，对于特定的问题使用相应的编码方式可以得到更高的性能。本文采用二进制与十进制相结合的编码策略，使得遗传算法的搜索范围和搜索效率都提高了。

表1中前面四项是用十进制编码，后面四项是用二进制编码。几何图形数量，几何元素边长，几何元素类型和何种图形是构成图形相似性特征的信息。

表1 零件编码信息

每个零件都有一个零件编号，以便于标识。旋转角度可以取0°到360°，但是为了搜索速度的加快，可以取10度的倍数进行搜索。几何元素的数量相等或相近是区分图形十分相近的重要前提。几何元素边长是为利用相似度计算公式所需要的必要条件。何种图形用4个二进制位用来表示，其中首位的0，1分别表示规则图形和不规则图形，如三角形为0000，矩形为0010，梯形为0100。几何元素类型包括直线段00，圆弧10和曲线01。最后两位用二进制判断是否需要填充和靠接。

2.3 排样原则

在板材上排样时，要尽量选择一个最佳匹配方案，由于本文需要处理的是规模较大的规则图形和大量的不规则多边形，如果采用经典的遗传算法收敛到最优解或者接近最优解的次优解的时间都是令人难以接受的，因此必须改进算法来提高收敛速度。从而本文提出了通过计算两个或者多个图形的相似度，进而对一部分图形进行归类，达到简化计算，加快搜索速度的目的。

2.4 相似度计算

2.4.1 拓扑结构和几何形状相似性

定义1 如果两个图形构成的几何元素的数量相似以及其连接顺序也一一对应，则称这两个图形的拓扑结构相似。

定义2 如果两个图形满足拓扑结构相似，且其几何元素的连接方式也一样（指的是垂直连接、锐角连接、钝角连接、相切连接）则称这两个图形几何形状相似。

为了比较图形的几何相似性，除了采取上述定义下的几何相似判断方法，本文还通过画圆形区域来达到计算顶点重合程度作用，拓展了几何相似性的定义。

2.4.2 相似度计算方法

本文通过采取图形间部分顶点重合后再计算图形的几何相似性的方法，并且采取轴对称兼容与线序倒转兼容的方式，从而进行两个多边形的相似性比较。

几何相似性的计算既为在相同拓扑结构下，几何元素相同的数目的多少决定相似程度的大小。由此，本文得出图形A和B的相似度为Qs（AB），Qs（AB）可以用式（5）表示

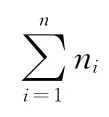
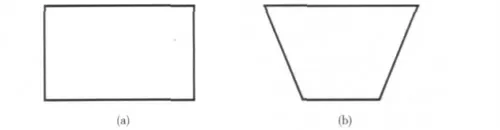
图2 相似度计算示例

相似度计算具体操作如下：

（1）从磁盘中读取图形文件，并得到矢量信息。

（2）将两个图形进行消除毛刺工作。

（3）将右边输入的图形通过拉伸变换，旋转，轴对称翻转等操作，使其能够消除干扰因素，与左边输入的图形处在各自坐标轴上相应的位置，从而方便下一步的操作。

（4）取左边图形的某个顶点，设定一个合适的圆形区域半径，然后进行顶点重合操作。即如果右边图形在这一范围内有一个或者多个顶点，则认为这一个或者多个顶点视作与左边图形对应的一个顶点。采用相似度计算公式，则可以计算出相似度。

圆形区域选取如下：以一个顶点为圆心，以很小的距离作半径，画一个小圆，只要另外一个或几个顶点在圆内或圆上，即视为重合，如图3所示。

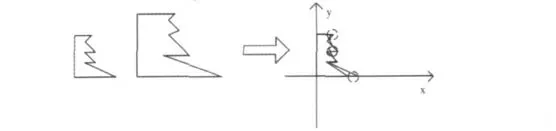
图3 圆形区域的选取

2.5 适应度函数设计

在优化排样问题中，传统方法往往只把排样布局的结果高度作为适应度函数的唯一参数。但是排样优化的目标是提高材料利用率，而且排布最高点的位置也会影响适应度函数。所以综合考虑以上三点因素我们定义适应度函数为f（x），可以用式（6）表示

式中：g（χ）——材料利用率，h（χ）——排样图的高度，l（χ）——排布最高点中最左边顶点的x坐标。α，β，γ为权重，取α＝0.5，β＝0.3，γ＝0.2。

2.6 碰撞算法

在不规则排样过程中，临界多边形（NFP）被广泛用于计算两个多边形之间相互接触的靠接位置，并求出可能的靠接位置，使排样过程成为多边形靠接时零件排放位置的定位优化问题。临界多边形NFP是这样得到的：先把其中一个多边形A 固定，另一个多边形B 上有一点P，B 在A的轮廓周围沿A的轮廓线滑动，由P点形成的多边形就是NFP，NFP有这样的性质：如果上述多边形B 摆放时，若P处于NFP内，则A 与B相交；若P处于NFP边界上，则A 与B刚好接触；若P处于NFP外，则A 与B 之间存在间隙。所以，NFP法可用于求解新摆放零件相对于己经摆好零件的可行定位。

临界多边形法如图4所示。

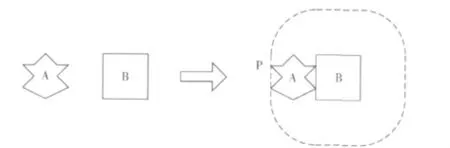
图4 临界多边形法

2.7 算法描述

（1）输入起始的几何图形，读取几何图形的矢量信息。

（2）对几何图形进行编码操作。

（3）判断输入的图形是否是规则图形，如果是，则对规则图形进行队排，拼接操作，否则，再判断它是否大于最小矩形包络率。如果是，则进行矩形包络，否则，再进行不规则图形的相似度计算，并判断是否大与阈值。如果是，则归类，否则，等待后续操作。

（4）利用图形序列构成一个按面积从大到小排列的染色体，然后根据现有的图形信息随机生成10个初始种群。

（5）计算适应度值f，并判断f是否满足终止条件，以及迭代次数是否达到100代。如果是，则跳到（9），否则，进行交叉操作。

（6）采用OX 顺序交叉算子进行交叉，并且编码过程中，当零件编号发生变化时，几何元素数量，几何元素边长，几何元素类型和何种图形都要随之变化。并且只能够序号与序号进行互换，旋转角度与旋转角度互换，它们之间不可以进行交叉变换，交换之后根据多边形的信息得出是否需要填充，并进行相应操作。

（7）然后进行变异，在变异算子选择上，选取了互换变异。互换变异就是随机的选择两个位置，并将这两个位置上的零件相互交换，变异概率取0.1。

（8）再进行个体选择，复制组成新一代种群，并且第一个染色体为适应度值最高的染色体。在选择过程中，搜索历史，如果产生的染色体没有出现过，则加入新一代种群，否则不加入。

（9）最后经过100代迭代之后，得到最优解，通过解码便可以得到排样结果图。

算法流程如图5所示。

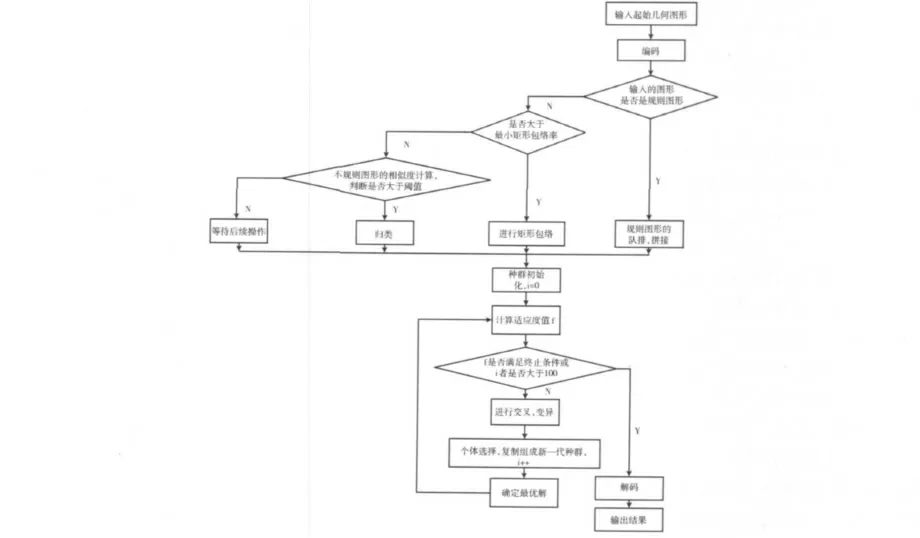
图5 排样算法流程

3 仿真与结果分析

为了验证本算法的优越性，在VS2010.net系统下，电脑配置为CPU：Intel Core i3 M350＠2.27GHZ，内存：2GB，操作系统：Windows7的PC机下实验。

（1）输入给定的图形，在一块足够大的板材上进行排样。在验证过程中取种群规模为N＝10，交叉概率为0.5，变异概率为0.1，设定进化代数为100。总共进行3次实验，分别排入30个零件，50个零件和80个零件，如图6、图7和图8所示。

由图6，图7和图8可知，随着图形数量的不断增大，改进的遗传算法能够使图形的占有率显著增加，但是运行时间也急剧增加。

（3）运用本文算法在MATLAB7.1平台下进行仿真实验，用本文算法与遗传算法GA 对25个矩形件进行排样，结果如表2和图9所示。图9中左图为本文算法的排样结果图，右图为GA的排样结果图。

表2 本文算法与GA 对25个矩形件排样结果

4 结束语

本文通过对大规模零件和不规则石材下料优化排样进行研究，提出了一种改进的遗传算法来求解此问题。针对遗传算法排样占有率低，处理时间长的缺点，在排样过程中首先对图形进行预处理，从而方便后续的排样操作。然后采取了混合编码方式，对于本文特定的石材下料问题得到了比单独使用一种编码方式的更好的排样效果。随后在排样原则上，提出了基于矢量图形信息的相似度计算方法，对不规则图形进行归类，并采用临界多边形方法进行碰靠，确定零件的位置，提高了排放的速度。通过实验，本文算法在处理大规模零件和不规则石材下料优化排样问题上能够得到不错的占有率，并且在占有率和时间复杂度上均优于传统的遗传算法。但是由于本文算法比较复杂，对于时间复杂度的研究还有待于进一步提高。

［1］Mitsukuni，Matayoshi.Two dimensional rectilinear polygon packing using genetic algorithm with a hierarchical chromosome［C］／／Anchorage，Alaska，USA：IEEE International Conference on Systems，Man，and Cybernetics，2011：989－996.

［2］YAO Fang，LUO Jiaxiang，HU Yueming.Solving two dimensional rectangular boards packing and stacking problems with discrete differential evolution algorithm［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2012，24（3）：406－413（in Chinese）.［姚芳，罗家祥，胡跃明.二维板材组包排样问题的离散差分进化算法求解［J］.计算机辅助设计与图形学学报，2012，24（3）：406－413.］

［3］SONG Yanan，XU Ronghua，YANG Yimin，et al.Study on application of hybrid algorithm on parking［J］.Computer Engineering and Applications，2009，45（34）：17－20（in Chinese）.［宋亚男，徐荣华，杨宜民，等.混合算法在排样问题上的应用研究［J］.计算机工程与应用，2009，45（34）：17－20.］

［4］LIU Huyao，HE Yuanjun.2D irregular nesting algorithm based on gravity center NFP［J］.Chinese Mechanical Engineering，2007，18（6）：723－731（in Chinese）.［刘胡瑶，何援军.基于重心NFP的不规则形状排样算法［J］.中国机械工程，2007，18（6）：723－731.］

［5］TANG Jiangang，LIU Cong，ZHANG Lihong.Irregular graph stock layout based on improved genetic algorithm［J］.Computer Engineering，2010，36（21）：185－187（in Chinese）.［唐坚刚，刘从，张丽红.基于改进遗传算法的不规则图形排样［J］.计算机工程，2010，36（21）：185－187.］

［6］CHEN Duanbing，HUANG Wengqi.Greedy algorithm for rectangle－packing problem［J］.Computer Engineering，2007，35（4）：160－162（in Chinese）.［陈端兵，黄文奇.求解矩形Packing问题的贪心算法［J］.计算机工程，2007，35（4）：160－162.］

［7］ZHANG Pengcheng，ZHANG Rongjie.Solved rectangle’s NFP by polygon segmentation［C］／／CangZhou，China：IEEE International Conference on Power Eng，Hebei Eng ＆Tech Coll，2011：1625－1628.

［8］LIANG Lidong，YE Jiawei.Research of irregular parts packing with genetic algorithm［J］.Computer Engineering and Applications，2009，24（2）：223－228.［梁利东，叶家伟.基于遗传算法的不规则件优化排样研究［J］.计算机工程与应用.2009，24（2）：223－228.］

［9］SONG Xiaoxia.Improvement and implementation of technology of initial population in genetic algorithm［J］.Computer Engineering and Design，2007，28（22）：5484－5487（in Chinese）.［宋晓霞.遗传算法中初始群体技术的改进与实现［J］.计算机工程与设计，2007，28（22）：5484－5487.］

［10］CHEN Shijin，CAO Ju.Heuristic algorithm for rectangular cutting stock problem［J］.Computer Engineering and Applications，2010，46（12）：230－232（in Chinese）.［陈仕军，曹炬.矩形件优化排样的一种启发式算法［J］.计算机工程与应用，2010，46（12）：230－232.］