改进PSO算法求解具有柔性生产路径钢铁产品分配问题
2013-07-03金春华
金春华,王 雷
(1. 北京信息科技大学 经济管理学院,北京 100192;2. 北京科技大学 东凌经济管理学院,北京 100083;3. 钢铁生产制造执行系统技术教育部 工程研究中心,北京 100083)
0 引言
企业在每个时期都会集中制定产品的销售计划,按照产品的种类和区域市场来划分产品的销售量,销售人员根据企业的销售计划,有指导的接受产品订单。订单来至不同的区域市场,集中到企业进行生产。如果企业接受的订单集中在某些区域,在企业生产能力有限的情况下,企业的产品生产就会影响前期制定的销售计划,打乱企业的生产销售战略。针对企业生产销售状况,企业应该在满足产品区域市场的需求量满足原则下进行产品分配。因此,企业在产品分配的过程中,不仅要将企业的盈利能力最大化作为目标,同时还要从企业长期战略发展出发,协调好各区域市场之间的关系,以市场产品需求满足率为导向,进而达到提高区域市场企业的满意度最终提高企业的长期盈利能力。由于企业自身产能的限制,在产品分配过程中要不断提高生产线设备的综合利用率,充分发挥企业的生产能力。此外,企业产品如果存在多条生产路径,不同生产路径生产出的产品具有不同的生产成本,在产品分配过程中尽可能选择成本最小的生产路径来提高企业的利润率。因此,多目标产品分配问题的解决对企业的生产销售实际有重要的影响。
陈菊新等[1]建立了产品分配的时变模型,并将其分为两层子问题。下层子问题为基本的运输问题,按一般的线性方程求解,上层子问题采用遗传算法进行求解,实验取得较好的效果。唐加福[2]考虑了全球制造环境下多产品生产分销网络问题,提出了基于拉格朗日松弛的两层分解启发式算法来求解包括生产商指定的生产任务、生产批量、生产商和分销商之间的交货量的联合决策模型。张翠华等[3]针对多供应商环境下JIT采购的订单分配问题,提出在满足一定送货及时率及采购策略条件下生产商的总采购成本最小化模型,通过企业实例仿真求解出较好的结果。潘伟等[4]通过考虑订单分配信息的不确定性和模糊性,构建一个包含模糊目标、模糊权重和随机约束的订单分配模型。然后,利用数值算例证明了模型的可行性。刘晓冰等[5]建立了以企业集团订单排产量最大和集团利润最大为目标的钢铁企业订单分配多目标优化模型,提出了模型求解的算法流程,最后通过实例验证了模型和算法。姜意扬等[6]建立基于物流供应商具有的订单、物流能力可获得性、配送效率、缺失率与成本的供应商选择与订单分配组合优化模型,并采用相应算法进行算例分析。Calvete等[7]分析由于供应商和分销商有各自的目标,不能实现产销计划的最优。他们在两阶段供应链环境下利用蚁群优化方法得出了一体化产销优化配置,平衡了供应商和分销商之间的分配关系。Kawtummachai等[8]研究了供应链条件下的订单分配流程,建立了数学模型。目的使总购买成本最小和维持特定的服务水平,通过求解算法证明了模型的可行性。
现有文献大多是研究企业在收到客户订单后,如何安排产品生产最后送达给客户,而很少有研究根据现有销售计划的指导,将不同工艺路线生产的产品分配到各区域市场的客户,达到生产线和市场需求的平衡。本文在考虑市场产品满足率的基础上,综合考虑了钢铁企业经营总利润和不同工艺路线上生产线上设备的利用率,建立柔性生产路径钢铁产品分配模型,设计多目标改进粒子群优化算法求解,通过实验考察模型和求解算法的可行性和有效性。
1 问题建模
1.1 问题描述
钢铁企业的每种产品生产具有多条工艺路线,同时产品具有多品种、小批量的特点,而市场对产品需求也是多种多样。那么,钢铁企业的产品分配问题是在满足生产和市场约束的条件下,确定各种产品大类和具体产品的产量,使得问题的目标函数最优。在钢铁企业经营环境下,产品分配问题以各市场需求为导向,在确定各种产品总产量的同时,还需确定分配至各市场上的产品产量。而同种产品可能来至不同的生产工艺路线,各生产工艺路线由不同的生产线构成。考虑到钢铁企业的生产情况和各市场的需求情况,问题存在以下约束:1)产品的品种大类不得超出最大量限制;2)各类产品的产量受到生产线生产能力限制,不得超出各生产线的最大产量;3)由于生产加工工艺的特殊要求,某类产品的产量存在最小值约束;4)各类市场对于各类产品的需求量均存在期望上限,因而,钢铁企业分配给各市场的产品量不能超过市场的最大需求量;5)各市场对某类产品存在特定需求,企业将此类产品分配给各市场的产量不得小于最小需求量。
在制定产品分配方案时,钢铁企业需要满足各市场需求为导向,综合考虑以下问题:1)产品生产利润最大化原则;2)生产线上设备的最大平均利用率原则;3)满足各市场产品需求,达到各市场产品需求最大化。所以,本文研究的柔性生产路径钢铁企业产品分配问题以最大化利润、设备利用率以及市场产品满足率为优化目标。
1.2 符号定义
1) 下标符号
i为产品品种编码,i∈I;
l为产品工艺路线编码, l ∈ ∪P Li, i∈I ;
m为市场编码,共有M个市场,1≤m≤M;
j工艺路线上的节点数(生产线)j=(1,2,… ,Nl),Nl为第l条工艺路线的最后一个节点;
k为实际生产线的编号 k =(1,2,… ,K)。
2) 集合
I为产品品种集合;PLi为产品i的生产工艺路线集合,i∈I;MPm为第m个市场需要的所有产品集合,1≤m≤M。
3) 参数
Maxk为第k条生产线的最大生产能力;
Mink为第k条生产线的最小生产能力;
Piml为第l条产品工艺路线上生产的产品i在市场m上的单位利润, i ∈ M Pm,1 ≤ m ≤ M , l∈PLi;
MaxMpim为市场m对产品i的最大需求量,i∈ I , 1 ≤m ≤ M ;
MinMpim为市场m对产品i的最小需求量,i∈ I , 1 ≤m ≤ M 。
4) 变量
zmiml为第l条工艺路线上生产的产品i在m市场的需求量, i ∈ M Pm,1 ≤ m ≤ M , l∈ P Li。
1.3 问题模型
以企业利润最大化、生产线上设备平均利用率最大化、市场产品满足率最大化为目标,本文建立了多目标产品分配模型为:
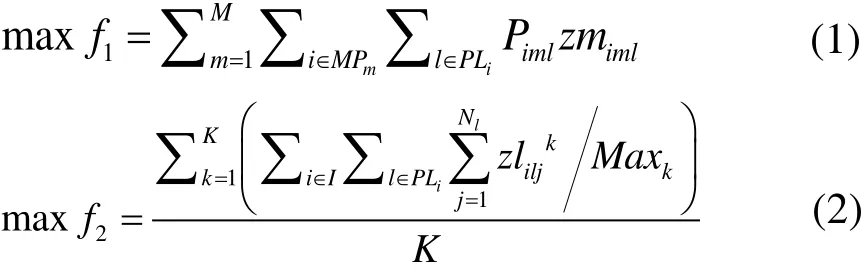

目标函数(1)表示企业利润最大化;目标函数(2)表示生产线上的设备平均利用率最大化;目标函数(3)表示最大化市场产品满足率;约束(4)表示生产线上的产出量不能大于规定的最大量;约束(5)表示生产线上的产出量不能小于最小量;约束(6)表示企业的产品销量不能超过市场需求产品的最大需求量;约束(7)企业的产品销量必须满足市场需求产品的最小需求量;约束(8)为平衡约束,即产品的产量必须等于其产品的需求量;约束(9)(10)定义了产品的分配去向与产量之间的关系;约束(9)~(12)为变量取值约束。
2 求解算法
上述建立的钢铁产品分配模型是一类多目标、多约束和多变量的组合优化问题,由于变量具有很大的维数,解的搜索空间大,不能够用精确的算法在有效的时间内求解。同时,多目标优化问题要综合考虑多个子目标之间的联系,使得问题的求解难度更大。因此,智能优化算法提供了这类问题的求解技术。粒子群优化算法(Particle Swarm Optimization, PSO)是由Kennedy和Eberhart[9]通过模拟鸟群觅食行为而提出的一种基于群体协作的随机搜索算法。由于粒子群算法具有参数少、全局优化效果好、收敛速度快的优点,该算法在许多多目标优化问题中得到了较好的应用[10-11]。
基本粒子群算法的数学模型如下所示:
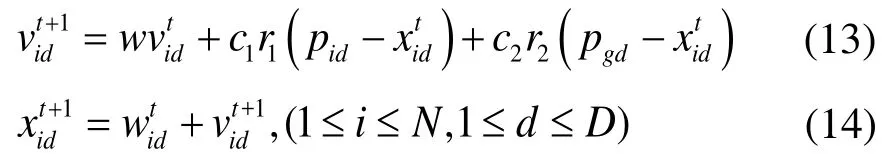
其中,w称为惯性权重,通常取0.9~0.4;c1、c2称为加速因子,通常取c1=c2=2;r1、r2为(0,1)之间的随机数。
2.1 初始解的生成
产品分配模型中有很多复杂的约束条件,使用随机生成初始粒子群和初始解的方法能够产生无效的粒子。本文研究的钢铁产品分配问题,可将各不同生产路径下的产品在不同区域市场上的分配量和不同生产线上的产品量映射为变量量的取值范围映射为变量的值域 D (zmiml,)= [ 0 , ∞),产品生产和分配约束映射为约束集合C,则产品生产和分配问题就能够转化为约束满足问题。对于具有复杂约束关系的约束满足问题,可以通过变量选择、约束传播等方法,从变量的值域中消除非可行解进而获得较好的初始可行解。
2.2 设计适应度函数
粒子的适应度值是衡量粒子飞行位置好坏的标准,粒子群算法在搜索过程中根据适应度函数来评价解的优劣。由于粒子群进行的是随机搜索,会产生不符合目标函数值的解,所以本文引入惩罚函数来处理约束问题,将偏离目标函数的解进行惩罚,使约束优化问题转换成无约束优化问题。
将(15)~(17)作为本文改进算法的适应度函数,其中,W是一个足够大的正数, (x )+= m ax { x ,0}。
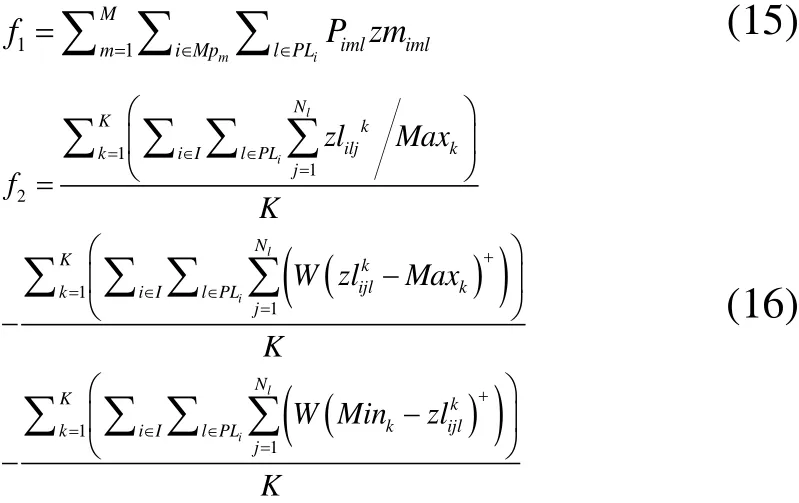
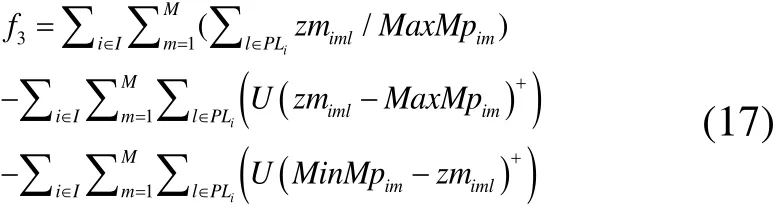
2.3 设置惯性权重
惯性权重值w对算法收敛性能的影响较大,较大的惯性权重能够得到很好的全局搜索能力,而较小的惯性权重有利于算法的局部搜索能力[12]。在算法的开始阶段由于种群的数量较大,所以应该采用较大的惯性权重,而在进化的后期保证算法收敛到最优值,强化局部搜索能力,选择较小的惯性权重。
由于惯性权重对于搜索策略的重要影响,本文采用动态调整w值的方法,随着迭代次数的不断增加,惯性权重的最大值按照公式(18)从0.9到0.4逐次减小,t为当前迭代次数,M为最大迭代次数[13]。

2.4 算法步骤
求解柔性生产路径产品分配问题的改进PSO算法步骤如下:
步骤1 初始化
2)令群体迭代数 t ← 0 ,加速系数 c1=c2←2,惯性权重 w ← 0 .9,最大寻优次数为MaxIter;
4)由约束满足算法求得的三个目标函数值作为初始粒子的适应度;
步骤2 更新粒子群
2)根据公式(13)和(14)更新粒子i的速度和位置,其中公式(13)中的惯性权重w根据公式(18)动态决定;
3)按照公式(15)~(17)计算更新后的粒子适应度,按照规则修改不可行粒子解,根据公式(15)~(17)重新计算修改后的粒子适应度;
步骤3 终止条件判断
1)令t←t+1,如果t>M,转2),否则返回步骤2;
2)输出粒子的适应度函数值,结束算法。
3 数据实验
3.1 实验设计
本文采用Microsoft Visual C++ 2008实现改进的PSO算法,实验环境为Pentium4/2.80GHZ/2.24GB/Windows7。实验数据来源于国内某大型钢铁企业。改进PSO算法参数设置为:种群规模大小为200;最大迭代次数为200。实验数据设置如下:产品种数n=5,10;需求市场数m=4,8;工艺路线数l=4,8;工艺节点上的最大产品量Maxk∈DU[1 0 00,2400];工艺节点上的最小产量Mink∈DU[1 0 ,80];不同工艺路线上产品对区域市场的最大分配量 M axMpim∈DU[2 50,700];不同工艺路线上产品对区域市场的最小分配量MinMpim∈DU[1 0 0,400],其中DU[ a, b]表示区间为[a , b]的离散均匀分布。根据产品种类、市场的分配量和产品生产工艺的不同,将实验分成6组,每组随机生成60个算例,采用企业产品利润、设备利用率和市场产品满足率三个指标评价算法的质量。
3.2 实验结果分析
改进PSO算法的算例中,随机选取一组数据作为实验的最终解,实验结果如表1所示,其中CPU为改进PSO算法的实际计算时间。
上述实验数据可以得到以下结论:
1)由表1可知,改进PSO算法在很短的时间内能够获得质量比较好的解。随着问题规模的增大计算时间增加,但是都是在可接受范围之内。
2)产品数量增加一倍可以引起利润额很大的提高,但是设备利用率和市场产品满足率都有一定的下降。
3)市场数量增加一倍可以引起需求满足率大规模的降低,利润额能够增加很小一部分,设备利用率减少不大。
4)工艺路线增加一倍可以引起利润额很大的提高,但是设备利用率和市场产品满足率都有一定的下降。
该数据实验符合实际情况,当钢铁企业向区域市场分配的产品种类增加时,不同种类产品的单位利润不同,增加的产品会带来利润的上升。由于品种的增多,设备的利用率和市场产品满足率会有一定幅度的下降。扩大产品的分配范围,企业产品利润和设备利用率不会有很大的变化,但是由于分配到区域市场的扩大,市场产品满足率就会下降。增加生产工艺路线的数量,扩大了现有企业的产能能力,但是设备利用率会有所下降。
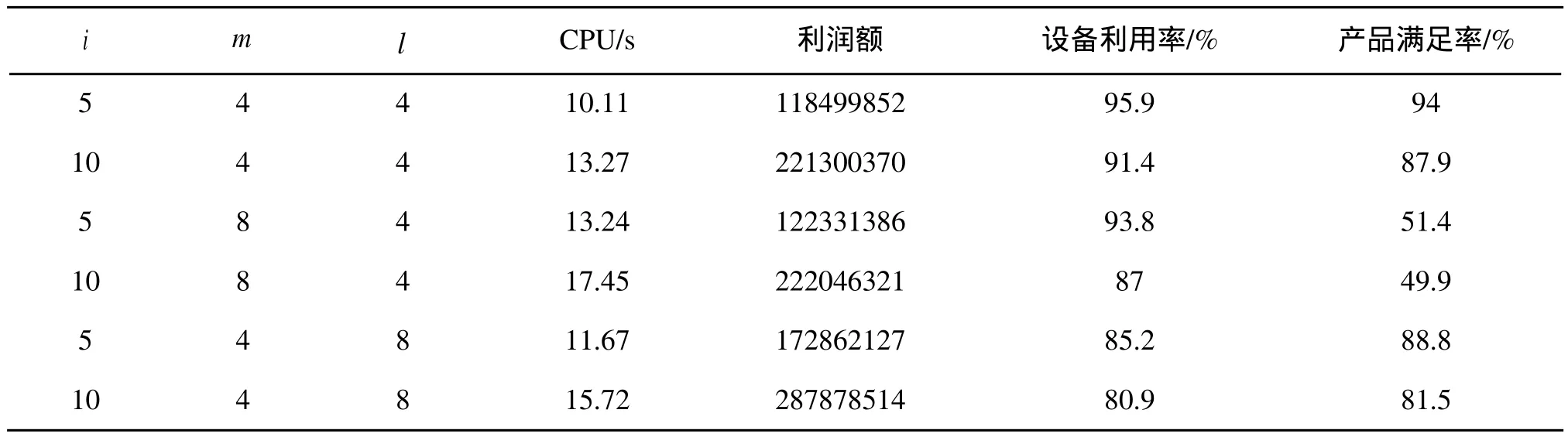
表1 实验结果
4 结论
由于钢铁企业生产线由柔性生产路径组成,如何把不同成本得到的产品有效分配到区域市场,如何在追求产品利润最大化的同时,考虑企业生产的综合设备利用率和市场产品满足率,是实现钢铁企业生产面对的新问题。根据钢铁企业问题的特点,建立了多目标的产品分配问题,考虑了企业利润、设备利用率和市场产品满足率为优化目标的模型,提出了改进PSO算法。算法由约束满足技术生成初始可行解,利用惩罚函数思想处理不可行解。实验表明算法能够在较短的时间内有效求解问题模型,实验符合现实问题,能够满足实际应用。
[1] 陈菊新,徐建闽,辛武平.基于遗传算法的产品分配方案研究[J].华南理工大学学报(自然科学版),2001,29(2):90-93.
[2] 唐加福.基于Lagrange松弛分解的多产品生产-分销系统的联合决策[J].机械工程学报,2005,41(8):153-157.
[3] 张翠华,朱宏,马林.基于JIT采购的订单分配问题模型及仿真应用[J].东北大学学报(自然科学版),2006,27(11):1291-1294.
[4] 潘伟,汪寿阳,华国伟,张金隆.基于模糊权重的多目标订单分配模型[J].中国管理科学,2009,17(2):80-85.
[5] 刘晓冰,王宇春.钢铁企业集团订单分配模型研究[J].控制与决策,2009,24(11):1629-1634.
[6] 姜意扬,王勇,邓哲峰.基于LSSC的供应商选择与订单分配[J].工业工程,2011,14(3):80-86.
[7] Herminia I.Calvete,Carmen.Gale.Bilevel model for production-distrbution planning solved by using ant colony optimization[J].Computers & Operations Research,2010,38(1):320-327.
[8] R. Kawtummachai, N.Van Hop.Order allocation in a multiple-supplier environment[J].International Journal of Production Economics,2005,93-94:231-238.
[9] Kennedy J, Eberhart R. Particle swarm optimization[C]//IEEE International Conference on Neural Networks(Perth, Australia), IEEE Service Center, Piscataway,NJ, 1995, IV:1942-1948.
[10] 张文学,李铁克.基于粒子群和约束满足的钢轧一体化批量计划优化[J].计算机集成制造系统, 2010,16(4):840-845.
[11] D.Y.Sha and H.Lin.A multi-objective PSO for job-shop scheduling problems[J].Expert Systems with Applications,2010,37(2):1065-1070.
[12] Shi.Y,Eberhart.R.A modified particle swarm optimizer[C].IEEE World Conf on Computational Intelligence.Piscataway:IEEE Press,1998:69-73.
[13] Shi Y, Eberhart R. Empirical study of particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation,1999:1945-1950.
