火箭助飞鱼雷入水点精度Bayes点估计评定方法

邵宗战，侯代文，房 毅

(91439 部队，大连 116041)

在入水点精度评估中，使用最多的是假设检验方法。该方法在代价函数最小准则下，先假设总体参数的分布形式，然后利用试验信息计算似然概率，进而确定接收原假设还是备择假设。假设检验方法在拒绝原假设时有充分的理由，但是在不能拒绝原假设时却没有足够的理由接受原假设，而工程检验的目的是要确认所关心的原假设是否成立，或者说待检验的产品是否合格，因此假设检验方法难以满足工程实践的需求。特别地，在入水点精度的考核中，假设检验方法一般将入水点偏差信息通过落入圆的划定转化为服从二项分布的成败型问题进行简化处理，在接受原假设时，不仅意味着不拒绝原假设，还可能会因为所作假设的差异，得到截然不同的结论;而且将精度问题简化为成败型问题，在客观上也造成入水点信息的损失，因此假设检验方法难以满足工程实践的需求［2］。

参数估计方法将入水点偏差看作服从某一分布函数的随机变量，利用试验信息估计变量的值，不仅解决了假设检验方法中接收原假设时的充分性问题，而且避免了入水点信息的损失。采用经典的参数估计方法进行入水点精度评估，仅仅利用定型阶段的试验信息，要得到置信度较高的评判结果，需要较多的试验样本。不同于传统的管装发射鱼雷，火箭助飞鱼雷试验属于破坏性试验，鱼雷不能回收使用，这会造成试验消耗大且组织、指挥和协调难度高，因而参数估计只能在小子样条件下进行。由于火箭助飞鱼雷在研制过程中，经历方案设计验证试验、科研试验等阶段，Bayes 点估计方法可利用这些阶段的入水点信息作为验前信息确定验前分布，并根据定型试验时获取的观测数据进行参数估计，在同样置信条件下，能降低试验所需鱼雷的条次数，从而有效地降低试验消耗、缩短试验周期、提高试验效率［3］。基于此，本文利用Bayes 点估计方法［4］对火箭助飞鱼雷入水点精度进行评定，仅利用较少的试验条次数，就能以较高的置信度，实现入水点精度的评定。最后，给出了相容性检验的计算方法，并通过应用实例对所提方法进行了验证。

1 Bayes 参数估计方法

Bayes 估计方法将鱼雷入水点位置看作服从正态分布的随机变量，将入水点偏差看作正态分布中的分布参数θ，并用概率分布函数描述参数θ 的未知状况。

首先，由验前信息确定验前分布π(θ)，由现场试验信息X={X1，X2，…，Xn}确定似然函数L(X|θ)，然后，利用Bayes公式综合现场试验信息和先验信息，形成较完备的后验分布在后验分布的基础上进行统计推断，就能够确定入水点精度的大小。

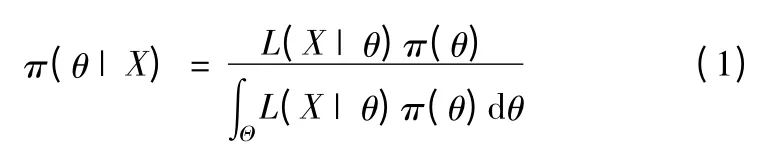
Bayes 方法在使用验前信息时要求信息以分布函数的形式表示，而指标评定过程中这些信息一般以历史数据、主观信息或者经验信息的形式存在，这就需要确定先验分布函数的形式并计算相应的参数。选取恰当的先验分布是正确反映先验信息并进行统计推断的前提和基础，目前选取先验分布的方法主要有共轭分步法、不变先验分布法等，在满足合理性要求的前提下，选取共轭分布能给估计带来极大的方便，在此选取共轭先验分布法进行研究。

1.1 分布假定［5］

对入水点精度指标σ，设D =σ2的验前概率密度函数π(D)为逆Gamma 分布IGa(α0，β0)，即:

以雷达所在位置为原点，在纵平面上，目标位置信息主要由观测距离r以及俯仰角θ来表征，其中观测距离标准差为σr，俯仰角标准差为σθ，则对应的协方差矩阵为

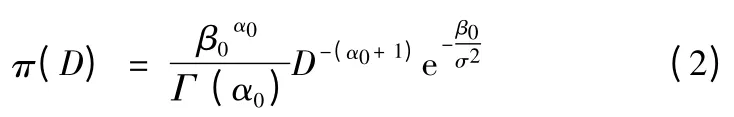
其中α0和β0是验前概率密度函数中的两个未知的分布参数，需要利用各种验前信息确定其取值。Γ(·)表示Gamma函数。

1.2 验前分布中超参数的计算

设定型试验之前，在以理论入水点为坐标原点的发射坐标系下，有m 个验前入水点信息{(Δx0i，Δz0i)|i =1，2，…，m}，其中(Δx，Δz)表示实际入水点相对于理论入水点的偏差。如果假定入水点偏差Δx ～N(0，D))，Δz ～N(0，D))，且Δx、Δz 相互独立，令

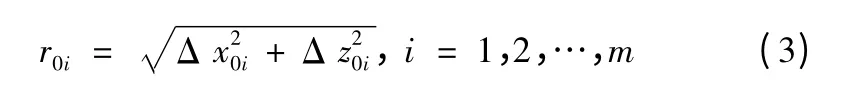
则r0i服从Rayleigh 分布，其概率密度函数:

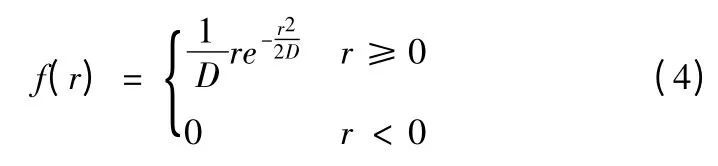
利用验前信息{r0i|i=1，2，…，m}，根据Bootstrap 方法［6］求出D 的验前均值和验前方差。在计算机上，该过程可利用Monte Carlo 方法按以下步骤实现:

1)以R1，R2，…，Rn的实现(r1，r2，…，rn)为有限总体，进行有放回地简单随机抽样，得到Bootstrap 观察值(，…)，并由此构造随机变量D 的一阶矩=R，…，;Fn)和二阶矩=R，…;Fn)。

计算得到随机变量D 验前概率密度函数IGa(α0，β0)中的超参数α0和β0。

1.3 验后概率密度函数的计算

如果定型试验中测量得到的n 个入水点信息为X ={(Δxi，Δzi)|i=1，2，…，n}。同样计算:

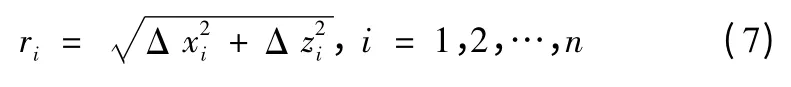
其中

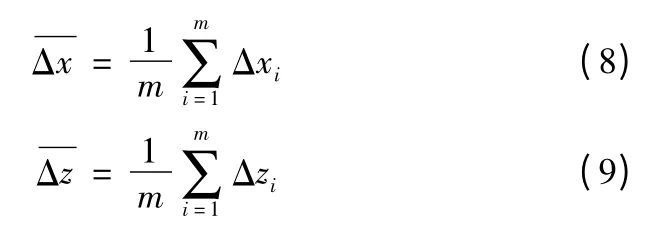
则似然函数为Rayleigh 分布函数的积:

根据Bayes 理论，随机变量D 的验后概率密度函数可以表示如下:

由于

则

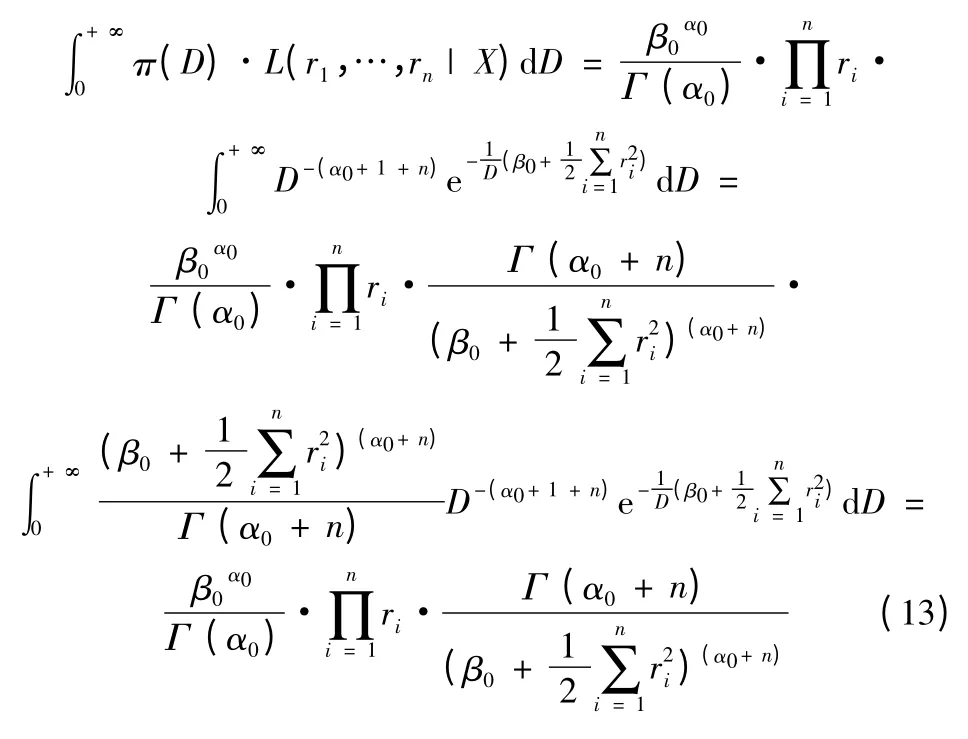
则D 的验后概率密度函数:

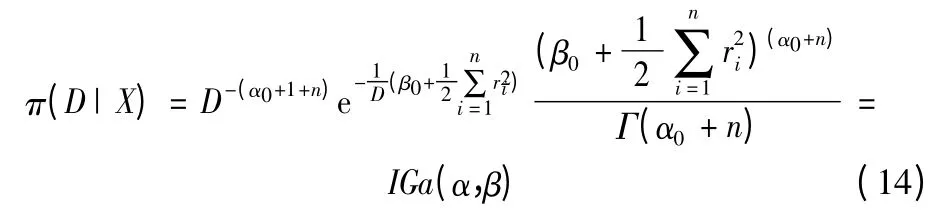
其中

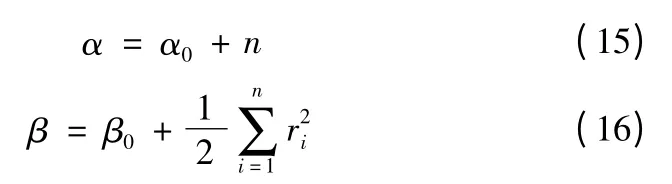
由于D=σ2，可求得标准差σ 的验后概率密度函数

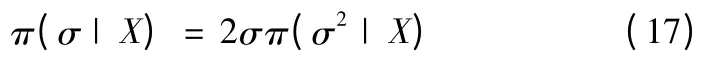
1.4 入水点精度估计

在均方误差最小意义下，利用式(12)得到入水点精度的贝叶斯点估计值

2 相容性检验

定型试验之前的验前数据是一种最常见的验前信息形式，当对验前数据直接运用Bayes 公式，实际上它是将验前数据与试验数据同等看待。此时，若两者不相容，将会降低评判结果的置信度，因此需要进行相容性检验，以确定验前信息是否可用。

相容性检验主要有Smirnov 检验、Wilcoxon 检验和Mood检验等方法。本文采用F 检验方法［7］确定验前信息与现场信息的相容性。

设x1，x2，…，xn1为验前信息中的一组入水点偏差，y1，y2，…，yn2为现场试验中的一组入水点偏差。作统计量:

对于给定的显著性水平α'，接受H'0假设的标准为P(F∈DA|H'0)=1-α'。即当F∈DA时，接受H'0，当F∉DA时，拒绝H'0，接受H'1。DA为检验的临界区域。对于F 检验，接收区域:

3 应用举例

假定入水点精度指标规定不大于190 m。在以理论入水点为坐标原点的发射坐标系下，验前入水点信息为{(256.76 m，12.57 m)，(366.29 m，342.25 m)，(-55.32 m，245.92 m)，(314.95 m，-145.14 m)}，由式(5)、(6)可计算出验前超参数α0=2. 712、β0=3192. 5。现场试验入水点信息为{(200.28 m，54.04 m)，(-289.50 m，-55.91 m)，(-97.50 m，- 193. 29 m)，(- 133. 43 m，289. 69 m)，(91. 52 m，-394.62 m)，(-24.64 m，-263.67 m)}，首先根据由式(21)，两组数据是相容的，再由式(15)、(16)求得验后超参数α=8.712、β=259 599。最后，根据式(18)得到入水点精度估计值为^σ=180.52 m。由于^σ≤190 m，入水点精度满足指标要求。

4 结束语

为了解决火箭助飞鱼雷系统复杂，试验子样数少，指标评定困难的问题，本文采用Bayes 点估计方法，融合各种验前信息对入水点精度进行评定。首先对验前信息与试验现场信息的相容性进行检验，以确定验前信息是否可用;然后利用两种信息分别计算验前和验后概率密度函数，进而确定入水点精度的概率统计结果，判定该项指标是否满足技术要求。最后通过应用实例验证了本文方法的有效性。

［1］程光显，张士峰.导弹落点精度的鉴定方法—概率圆方法［J］.国防科技大学学报，2001，23（5）:40-43.

［2］Kay S.Fundamentals of Statistical Signal Process，Estimation Theory［M］.Englewood Cliffs，NJ:Prentice-Hall，1993.

［3］王国玉，申绪涧.电子系统小子样试验理论方法［M］.北京:国防工业出版社，2003.

［4］GJB 6289—2008，地地弹道式导弹命中精度评定方法［S］.

［5］张金槐，唐雪梅.Bayes 方法（修订版）［M］.长沙:国防科技大学出版社，1993.

［6］Efron B. Bootstrap methods: another look at the jackknife［J］.Annals of Statistics，1979，7（1）:1-26.

［7］张湘平.小子样统计推断与融合理论在武器系统评估中的应用研究［D］.长沙:国防科技大学，2003.

［8］马锦垠，侯宝娥.火箭助飞鱼雷入水点测量系统的设计与实现［J］.火力与指挥控制，2012（8）:199-201.