电压型驱动按定子或气隙磁链定向的优势分析

陈增禄，刘娟娟，马 鑫，汪 冰，颜廷欣

（西安工程大学电子信息学院，西安 710048）

异步电动机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。矢量控制技术给出了交流电动机按磁场定向的解耦控制方法，具有磁链与转矩解耦且线性的控制模型，为交流电动机高性能控制奠定了基础[1]。

根据选择磁链矢量的不同，理论上可将磁场定向的矢量控制技术分为三种，分别是按转子、定子或气隙磁场定向控制；按照变频器输出控制变量的不同，可分为电压输出控制型和电流输出控制型。二者交叉排列，按磁链定向的矢量控制技术共有六种控制方案。

采用电流输出控制型变频器，且按转子磁链定向的矢量控制应用最为广泛。主要原因是其电磁转矩和转子磁链可实现彻底解耦，为系统动态设计带来很大的方便[2]。但是，为了实现电流型输出控制，一般要为变频器增设电流控制环；特别是转子磁链检测受到转子参数不易测量及随环境改变的影响，使得其低速性能不好[3，4]。为了弥补这一缺陷，学者们研究了多种方法，并积累了海量的文献。直至现在，检测和补偿转子参数的影响仍然是个研究热点[5-7]。

直接转矩控制也是应用很成熟的一种方案。该方法不依赖电机的动态数学模型和参数，因而鲁棒性好；直接采用“砰-砰”控制，因而动态响应速度快。其最大缺点是输出转矩脉动较大，因而不宜用于低速范围[1，8]。直接转矩控制的研究热点是通过空间电压矢量的扇区细分以减少转矩脉动[9，10]。

在矢量控制的六种控制方案中，除了上述广泛应用的电流输出控制型变频器驱动的按转子磁链定向的矢量控制方案外，其它五种方案具有一个共同的弱点，那就是通过坐标变换可以实现电机动态模型的线性化，但是无法实现磁链和转矩的完全解耦；但是从理论上讲，通过附加相应的“动态去耦项”（这正是本文理论分析的工作之一），上述五种矢量控制方案都可以实现完全解耦（且线性化）；而且解耦后的动态模型会更加简单，使得对磁链和转矩的动态控制效果会更好（这是本文将要重点证明的内容）。上述动态去耦项均需在数字控制器中实时求得，这对于早先计算能力较差的嵌入式微处理器来说可能无法承受，但是对于当前计算能力和速度都快速提高的微处理器来说已经微不足道了。

与电流控制输出型变频器相比，在工程上使用电压控制输出型的变频器更加方便，最典型的是空间矢量脉冲宽度调制SVPWM（space vector pulse width modulation）逆变器。但是在以电压输出型变频器驱动的三种磁场定向控制方案中，只有按转子磁链定向的控制方案受到了关注[2]，这大概是因为这时的“动态去耦项”最为简单，因而对微处理器的计算压力不大。但并没有摆脱转子参数对转子磁链检测的影响，事实上应用得并不多。本文将从理论上证明，使用电压输出控制型变频器驱动，按定子或气隙磁链定向时，尽管其“动态去耦项”依次更加复杂，但是去耦后得到的线性解耦的动态被控模型却依次更加简单；因而，其闭环解耦控制的动态性能依次显著变好。更重要的是，考虑到定子和气隙磁链的检测更加简单，且不再受转子参数的影响；因而，可以预期这两种方案必将受到关注。

1 不同磁场定向时的控制方程

采用电压输出控制型变频器，需要分别得到定子d轴电压usd与磁链ψ之间的传递函数，以及q轴电压usq与电磁转矩Te之间的传递函数。

1.1 三相异步电动机的动态模型

同步旋转dq坐标系上的磁链方程[1]为

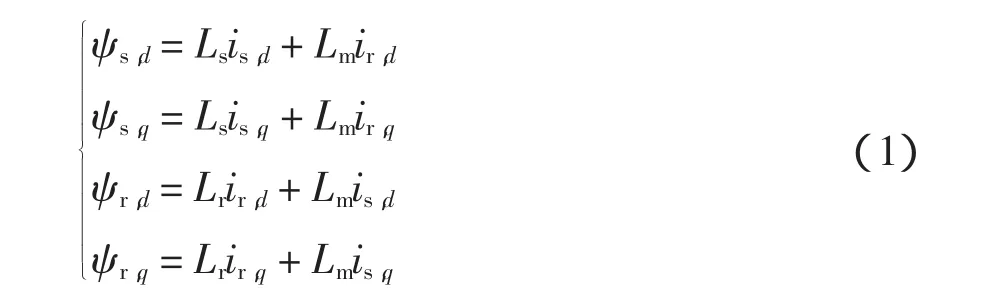
同步旋转dq坐标系上的电压方程[1]为

ω - ψs，d-is状态方程式[1]为

电磁转矩方程[1]为

式中：下标s、r和m分别表示定子、转子和气隙；u、i和ψ分别表示电压、电流和磁链；d和q分别表示d轴和q轴；p是微分算子，ω1是同步转速；ω是转速；ωs=ω1-ω是转差角速度；np表示磁极对数。

1.2 转子磁链定向

本节内容在文献[2]中有详细说明，不再写出推导过程，直接给出去耦项和控制方程

式中：us，d的最后一项包含了与 is，q的耦合项，us，q的最后一项包含了与ψr，d和is，d的耦合项，如下划虚线所示。为了实现 us，d和 us，q分别独立控制 ψr，d和Te的目的，在式（5）中分别定义去耦项

则去耦后式（5）成为

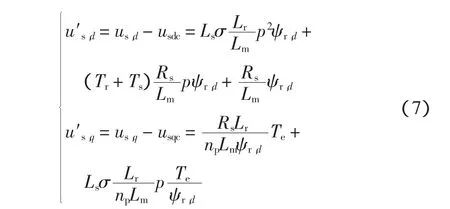
由上式可得完全解耦的线性传递函数为

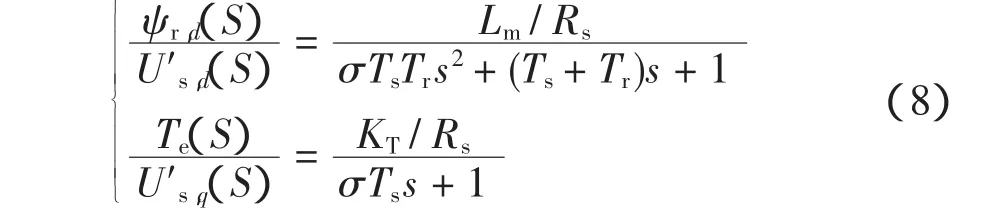
转矩计算公式为

交叉去耦的动态结构如图1所示。

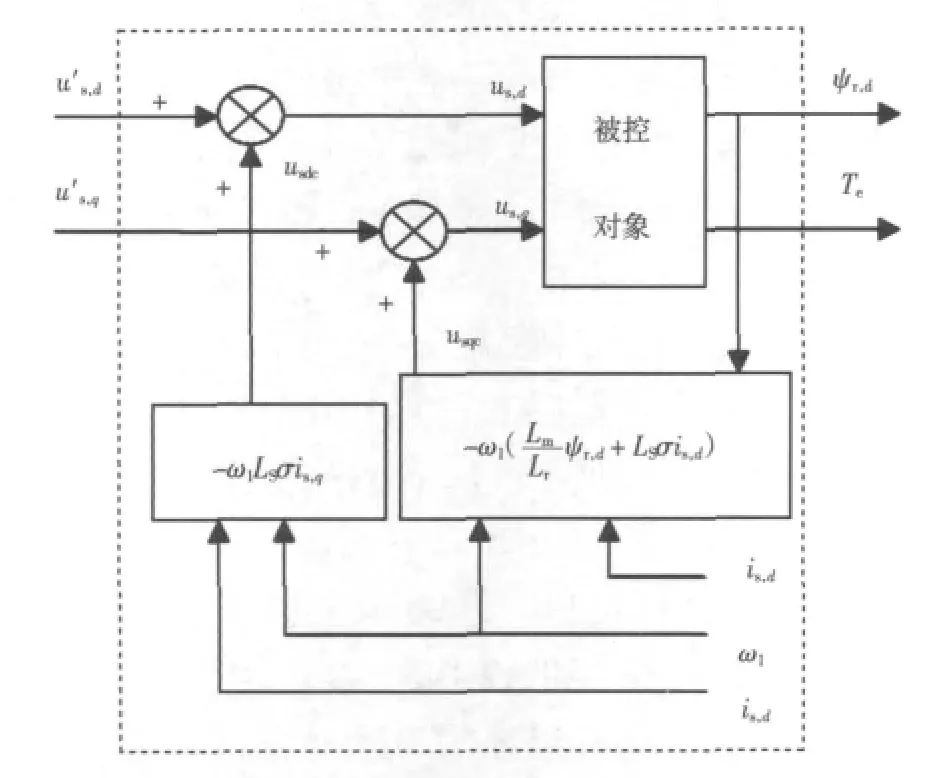
图1 按转子磁链定向时的交叉去耦动态结构Fig.1 Cross and decoupling diagram of rotor with flux orientation

从图1可看出，加上解耦项以后，从虚线框外往里看，系统变成一个两输入两输出线性解耦的控制系统。

1.3 定子磁链定向

取d轴沿着定子总磁链矢量ψs，d的方向，q轴逆时针旋转90°。则有

将式（10）代入式（1）的第 1、2 式求得 ir，d和 ir，q，然后再代入式（4），得到转矩公式

将式（1）的第 3、4式和式（10）代入到式（2）中的第3、4式，化简可得转差频率计算公式

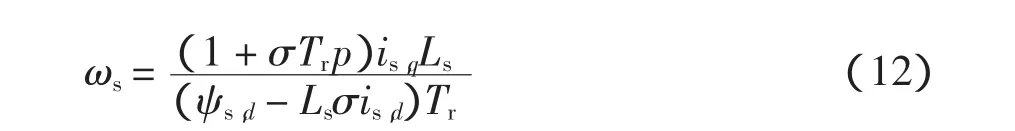
将式（10）代入式（2）的第一式可求得 is，d，由式（11）可求得 is，q，代入式（3）得到

式（13）中存在 is，q对 us，d的耦合项，以及 ψs，d、ω、ωs和 is，d对 us，q的耦合项。为了实现 us，d和 us，q分别独立线性地控制ψs，d和Te，分别定义去耦项

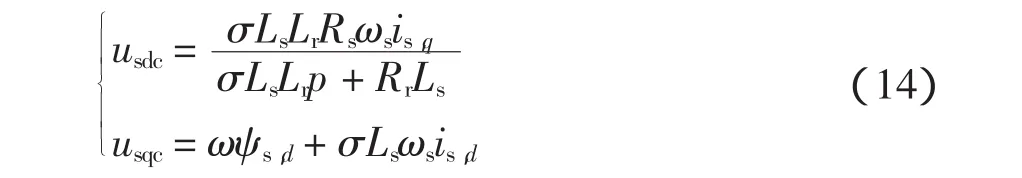
则去耦后式（13）成为

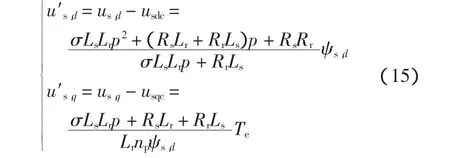
由式（15）可得按定子磁链定向时完全解耦的线性传递函数为

交叉去耦的动态结构仍为图1所示，只是将图 1中的耦合算式（6）用式（14）代替。与式（6）相比可见，去耦式（14）比式（6）略微复杂些。

1.4 气隙磁链定向

取d轴沿着气隙总磁链矢量ψm，d的方向，q轴逆时针旋转90°。则有

式中，m为气隙，下同。

按定义有

将式（17）代入式（18）得到

将式（19）代入式（4）得到转矩公式

将式（19）和式（1）代入式（2）化简后得到

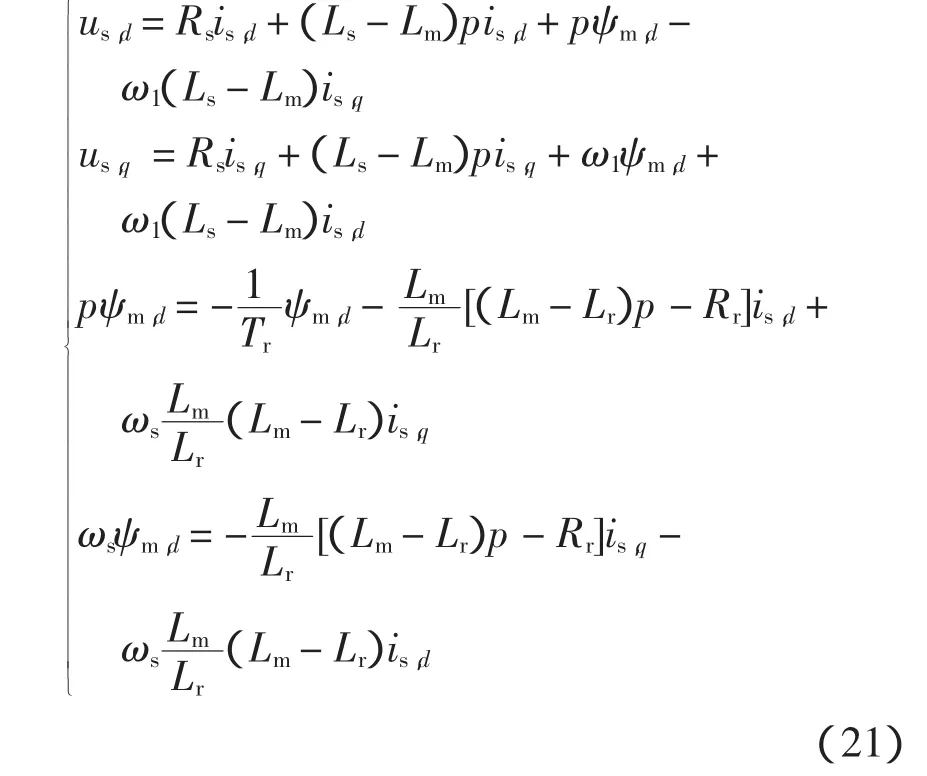
由式（21）的第4式得转差频率的计算公式

由式（21）的第 3、4 式可解出 is，d，由式（20）可解得 is，q，代入式（21）的前两式得到

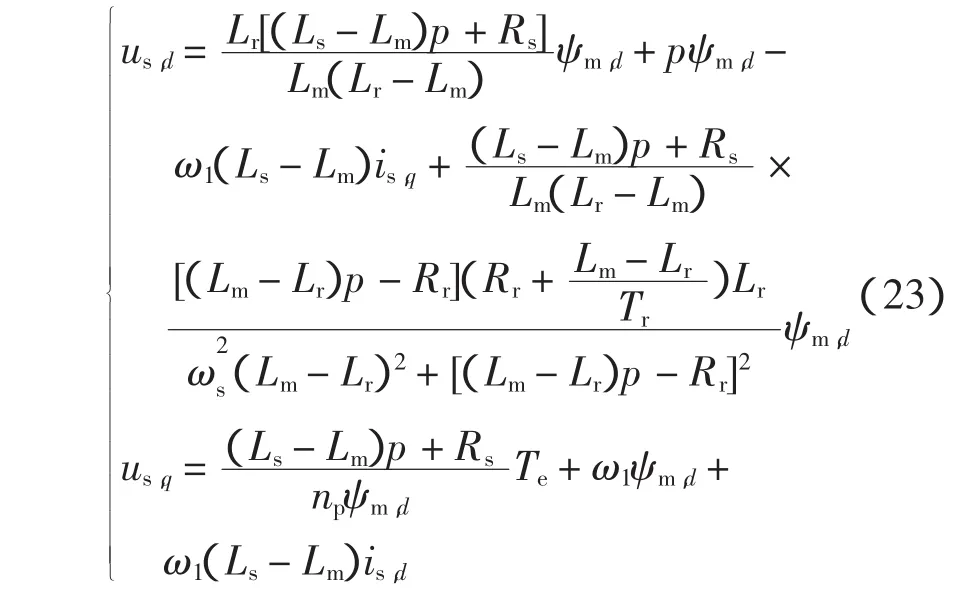
为了实现 us，d和 us，q分别独立控制 ψm，d和 Te的目的，分别定义去耦项

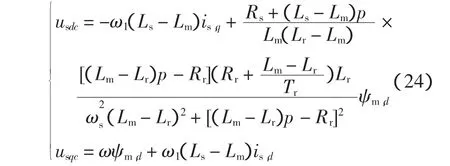
去耦后式（23）成为

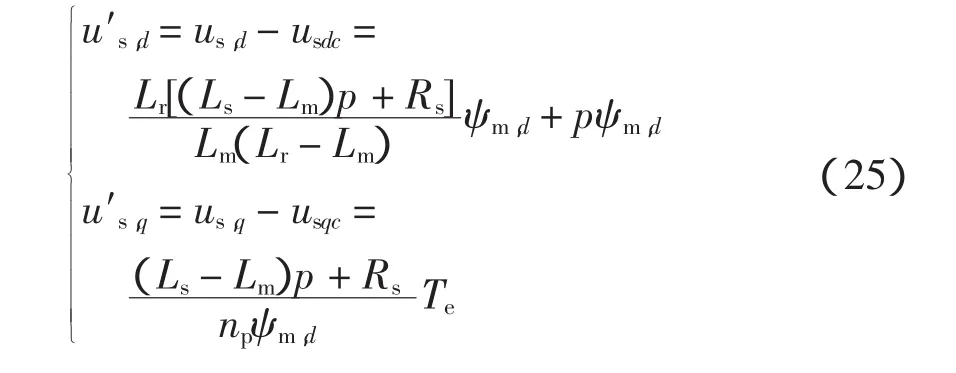
由式（25）可得按气隙磁链定向时完全解耦的线性传递函数为

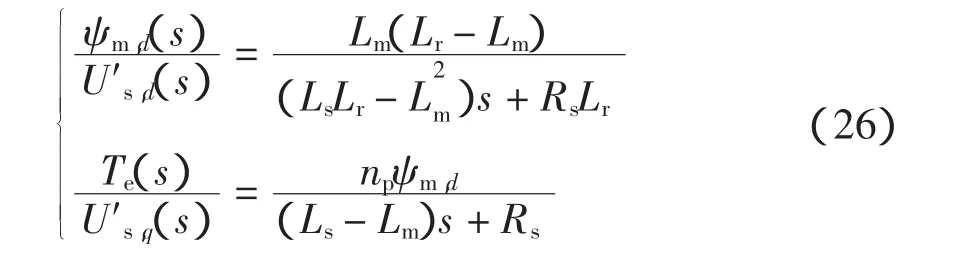
交叉去耦的动态结构仍为图1所示，只是将图1中的去耦算式（6）用式（24）代替。此时的去耦算式（24）显然过于复杂一些，事实上其计算量并不是太大，并且解耦后的传递函数较前两种磁链定向时更简单。

2 矢量控制系统仿真研究

2.1 仿真模型

在Matlab7.11.0（R2010b）的环境下，利用Simulink和SimPowerSystems模块可以分别构建按转子、定子和气隙磁链定向的矢量控制系统仿真平台，如图2所示。采用实验室现有实验平台的三相异步电动机实测参数。电机型号为Y90L-4，额定电压UN=380 V，额定电流IN=3.7 A，额定功率PN=1.5 kW，额定频率fN=50 Hz，磁极对数np=2，额定转速nN=1 400 r/min；实测参数定子电阻Rs=4.55 Ω，定子漏感 Lls=0.019 7 H，转子电阻Rr=3.77 Ω，转子漏感 Llr=0.019 7 H，定转子互感Lm=0.296 6 H，转动惯量 J=0.083 kg·m2，摩擦系数F=0.004 7 N·m·s。

图中虚线框可以分别表示去耦算式（6）、式（14）或式（24）。A1和A2相同，表示转矩环的反馈滤波环节，B表示转速环的反馈滤波环节，C表示磁链环的反馈滤波环节。采用SVPWM的电压输出控制型逆变器；检测两个线电压；右下角是测量模块，在不同的磁场定向控制时采用相应的算法，不再细述。

2.2 系统设计

限于篇幅，本文仅将3种系统及应用最成熟的矢量控制系统（按转子磁链定向，以电流输出控制型变频器驱动）的详细计算和设计结果列于表1，不再给出具体的设计过程。

2.3 仿真结果及分析

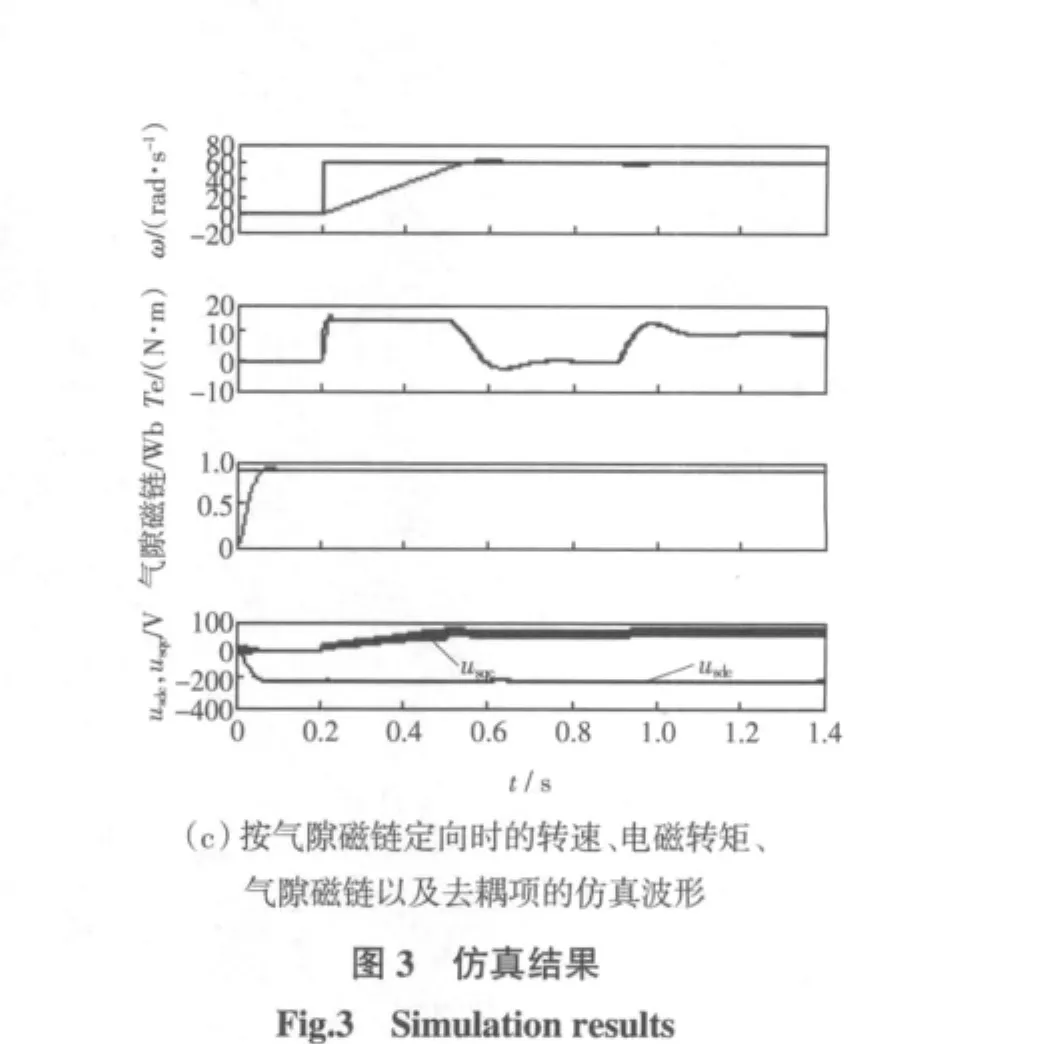
在图2的基础上按3种磁链定向时的仿真结果分别如图3所示。仿真时先空载起动，待磁链稳定建立后在0.2s时刻加入60 rad/s的给定转速。转速调节器加了积分分离，所以转速超调很小。在0.9 s时加入了10 N·m的额定负载转矩，由图可见，在整个动态过程中，磁链保持恒定，实现了转矩和磁链的解耦。

仿真结果表明，采用电压输出控制型的变频器时，无论按哪种磁链定向，起动和加载时，转速控制的过渡过程几乎完全一样；由于转矩环的带宽略有不同，使得按定子和气隙定向时的转矩跟踪控制性能依次更快一些；在转矩动态变化时磁链均可维持不变，表明转矩和磁链实现了完全解耦；定子磁链定向时的磁链环设计成为典型II型系统，所以较其他两种系统的磁链起动超调较大些。特别是从仿真结果中可以看出，对应三种不同的去耦量usdc和usqc，这是实现动态解耦的基础。

表1 分别按三种磁链定向时的系统设计结果Tab.1 Results of system design for the three field orientations

图2 分别按转子、定子和气隙磁链定向时的矢量控制系统仿真平台示意Fig.2 Simulation block diagram of rotor，stator and air gap with flux orientation vector control

3 结论

微处理器计算能力的提高为定子和气隙磁链定向的实现提供了可能。本文在电压输出控制型变频器驱动交流电动机的基础上，分别对三种磁链定向进行了理论分析、设计和仿真，结论如下：

（1）分别按转子、定子和气隙磁链定向时的控制方程都不能实现磁链和转矩的完全解耦控制。但是通过设计相应的去耦项，都可以得到完全解耦的线性传递函数。3种去耦算法依次更复杂些，但是去耦后的解耦控制传递函数数气隙磁链定向时最为简单。

（2）3种磁场定向的去耦算法和去耦后的解耦控制传递函数都与转子参数有关，因此去耦精度和被控对象的传递函数不可避免地会受到影响。

（3）受转子参数影响的去耦算法和解耦后的控制传递函数，由于其处于前向控制通道中，因此，只要处于反馈通道中的磁链和转矩检测能保证高精度，就可以有效抑制转子参数变化对系统控制性能的影响。由于定子磁链和气隙磁链的观测器可以不依赖转子参数，因而较转子磁链的检测更为准确；同样按定子和气隙磁场定向时的转矩运算公式亦不受转子参数的影响。

（4）使用电压输出控制型变频器比使用电流输出控制型变频器更为方便。

（5）综上分析，由电压输出控制型变频器驱动的定子或气隙磁链定向的交流异步电动机动态调速系统会具有新的更大的应用优势。

[1]陈伯时.电力拖动自动控制系统[M].北京：机械工业出版社，2000.

[2]李永东.交流电机数字控制系统[M].北京：机械工业出版社，2002.

[3]吕昊，马伟明，聂子玲，等（Lü Hao，Ma Weiming，Nie Ziling，et al）.磁场定向不准对感应电动机系统性能影响的分析 （Analysis of induction machine system performance influence about field-oriented inaccuracy）[J].电工技术学报（Transactions of China Electrotechnical Society），2005，20（8）：84-88.

[4]Bolognani S，Peretti L，Zigliotto M.Parameter sensitivity analysis of an improved open-loop speed estimate for induction motor drives[J].IEEE Trans on Power Electronics，2008，23（4）：2127-2135.

[5]王高林，杨荣峰，张家皖，等（Wang Gaolin，Yang Rongfeng，Zhang Jiawan，et al）.一种感应电机转子时间常数MRAS的在线辨识方法（Rotor time constant online estimation of induction motors based on MRAS）[J].电工技术学报（Transactions of China Electrotechnical Society），2012，27（4）：48-53.

[6]Toliyat H A，Wlas M，Krzemiriski Z.Neural-networkbased parameter estimations of induction motors[J].IEEE Trans on Industrial Electronics，2008，55（4）：1783-1794.

[7]Chen Zhenfeng，Zhong Yanru，Li Jie.Parameter identification of induction motors using ant colony optimization[C]//IEEE Congress on Evolutionary Computation.HongKong，China，2008.

[8]佘致廷，张红梅，何雯，等（She Zhiting，Zhang Hongmei，He Wen，et al）.感应电机DTC转矩与磁链模糊PI自校正控制（Fuzzy PI self-tuning control of flux and torque of induction motor DTC）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（3）：22-27.

[9]Buja G S，Kazmierkowski M P.Direct torque control of PWM inverter-fed AC motors-a survey[J].IEEE Trans on Industrial Electronics，2004，51（4）：744-757.

[10]顾德英，季正东，张平（Gu Deying，Ji Zhengdong，Zhang Ping）.基于 SIMULINK的异步电机的建模与仿真（Modeling and simulation of asynchronous motors based on SIMULINK）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2003，15（2）：71-73.