变速恒频风力发电系统最大风能追踪的控制

付明晓，李守智

（西安理工大学自动化学院电气系，西安 710048）

近年来，风力发电作为绿色可再生能源吸引了越来越多的关注[1]。采用双馈风力发电机（double-fed wind generator，DFIG）的交流励磁变速恒频（variable speed constant frequency，VSCF）风力发电技术以其独特的优越性逐渐成为风力发电的主流形式，该技术控制灵活，运行效率高，特别是在最大风能追踪方面可在较宽范围内变速运行。基于不同的变流器拓扑结构，以往的最大风能捕获方法[2-5]，根据原理大致可以分为叶尖速比（tip speed ratio，TSP）算法、功率信号反馈（power signal feedback，PSF） 算法和登山搜索 （hill climbing search，HCS）控制。TSR控制法需要实时精确地测量风速，这在实际现场较为复杂；PSF则需要找到风机转速和最大功率之间的准确关系，具体实施并不容易；传统HCS控制法是通过实时测量风力机转速和输出功率，利用经典数学寻优方法跟踪最大输出功率点。该方法避免了测量风速的问题，然而，此类方法一般需要预知风机参数，参数的准确性直接影响控制效果。

本文对传统的HCS方法进行改进，将输入参数由风力机的输出的机械功率改为发电机输出的电磁功率，并将其与矢量控制相结合，在不需要预知风速以及风机的一些参数的情况下，可以实现最大风能追踪以及有功、无功解耦控制，提高了控制精度及灵活性。Matlab/Simulink仿真验证了本文提出的控制策略的准确性和有效性。

1 风力机运行特性及双馈异步电机的解耦控制

1.1 风力机运行特性

由风力机空气动力学知，风力机的输入功率为

风力机通过桨叶捕获风能，并将风能转化为机械能[6]。由贝兹原理，风力机捕获的机械功率为

式中：v为风速；A为风力机桨叶扫掠面积；ρ为空气密度；Cp（λ，β）为风力机风能利用系数；λ为叶尖速比；β为桨叶节距角。

由式（2）可以看出，在风速v给定的情况下，风力机捕获的功率取决于功率系数Cp（λ，β），而Cp（λ，β）又是叶尖速比和桨叶节距角的函数[4]，即

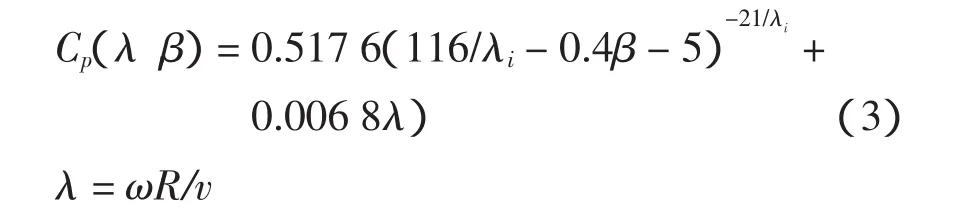
不同风速下风力机的输出功率特性（β=0°）如图1所示，其中Pmax线是各风速下风力机最大输出功率的连接线，即最佳功率曲线，且v3>v2>v1。可以看出为实现最大风能追踪，必须在v变化时实时的调整电机转速ωm，使风力机的输出功率最大。

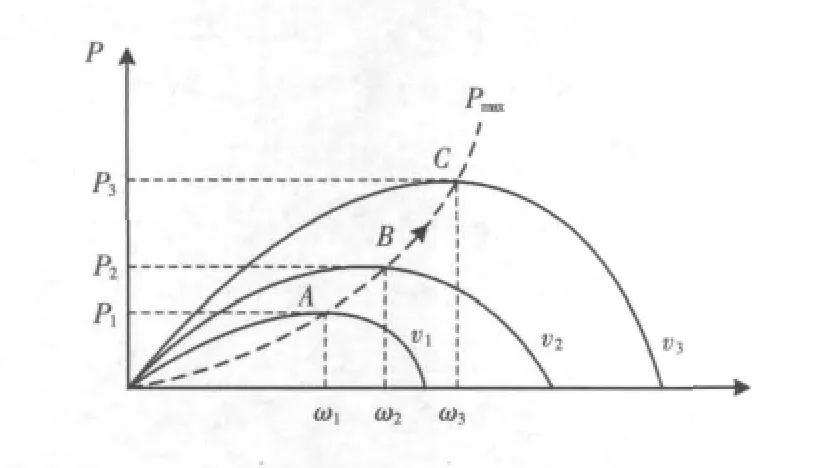
图1 风力机的输出功率曲线Fig.1 Output power curvs of wind turbine

1.2 定子磁链定向矢量控制

为了控制双馈感应发电机的转速，以及实现有功和无功的解耦，采用基于定子磁链定向的矢量控制策略。

定、转子绕组电压方程为

式中：Uds、Uqs、Udr、Uqr分别为定、转子电压的 d、q 轴分量；ids、iqs、idr、iqr分别为定、转子电流的 d、q 轴分量；Rs、Rr为定、转子绕组的等效电阻；ω1=100π 为同步转速，既dq坐标系相对于定子的角速度；ω为dq坐标系相对于转子的角速度，ω = ω1- ωr，ωr为发电机电角频率，它与机械角频率ωm的关系为：ωr=pnωm，pn为发电机的极对数；p 为微分算子，p=d/dt。

定、转子磁链方程为

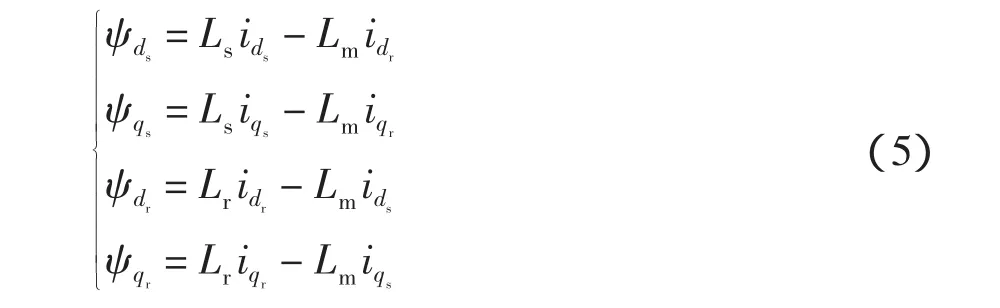
式中：ψds、ψqs、ψdr、ψqr分别为定、转子磁链的 d、q 轴分量；Ls、Lr分别为dq坐标系下定、转子绕组自感；Lm为定子绕组与等效转子绕组间互感。

运动方程为

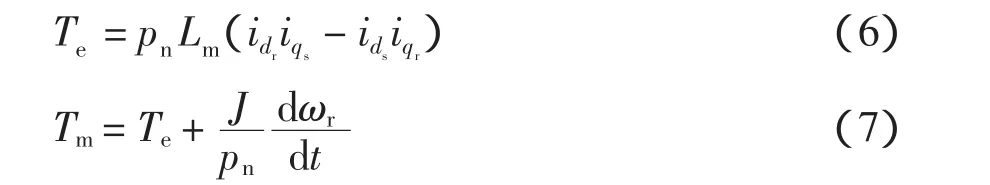
式中：Tm、Te分别为电机机械转矩和电磁转矩；J为电机转动惯量。

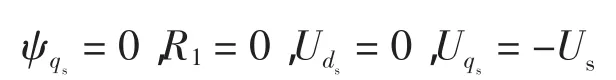
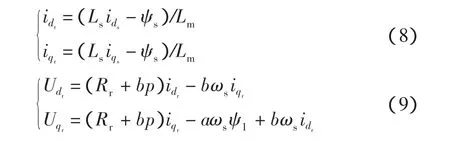
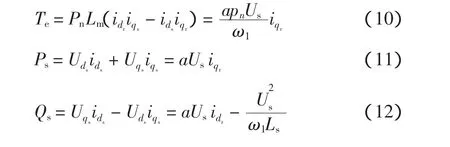
通过以上定子磁场定向，可实现双馈异步电机的有功和无功的解耦，为下述控制策略实现提供了方便。

2 基于改进的HCS法的MPPT控制策略

由图1可知，风力机在风速一定、转速变化时输出的机械功率是单峰曲线，只有一个最大功率点，而不同的风速下，也只有一个最大功率点。在最大功率点处，功率对转速的导数为零，这是登山搜索法的核心[7-8]，所以在最大功率点处，可得

由于风机输出的机械功率Pmec和发动机输出的电磁功率Pe有关联，而Pe在机侧定子磁链定向的矢量控制中很容易得到，所以对其进行转换，即

式中：Pmec为风力机输出机械功率；Pe为电磁功率；s为转差率，将式（14）带入式（13）得

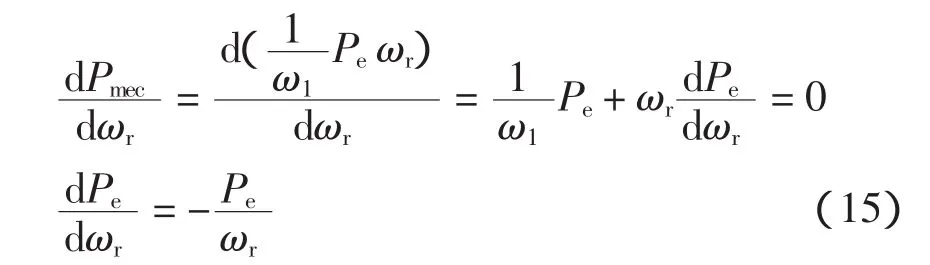
由式（15）可知，对于一定的风速，设最大功率点处的电机转速为ωopt，如图2所示，则有

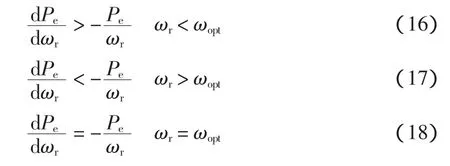
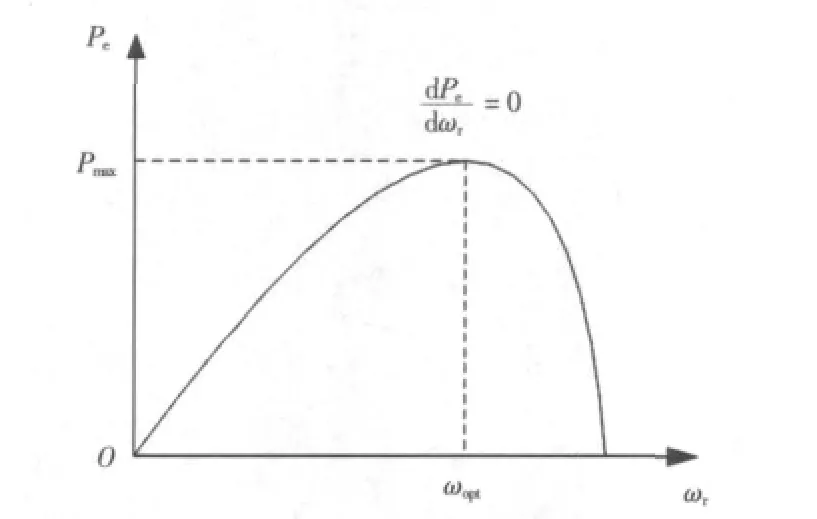
图2 风力机功率-转速曲线Fig.2 Power-speed curve of wind turbine

由式（16）～式（18）就可以得出电导增量法的最大功率点搜索方法，其实现方法如下：在n时刻和（n-m）时刻（即间隔m个PWM周期），对风力机角速度ωr进行采样，按照式（11）对电磁功率进行计算，计算风力机功率对角速度的斜率为

角速度变化的步长要和dPe/dωr的变化一致，dPe/dωr增大，Δω 随之增大；dPe/dωr减小，Δω 随之减小。所以，可以得出角速度变化步长的公式为

式中，K为角速度变化步长的扰动系数。

控制算法流程如图3所示。

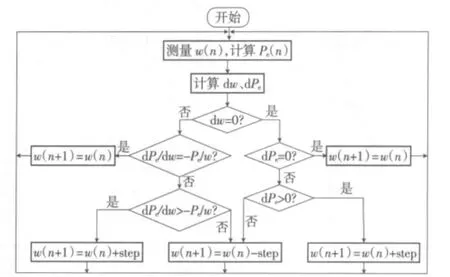
图3 MPPT控制算法流程Fig.3 Flow chart of MPPT control algorithm

将该最大功率点追踪算法和双馈电机的定子磁链定向矢量控制相结合，得出基于新型登山搜索法的最大风能追踪的完整控制策略如图4所示。采集双馈电机定子侧电压电流，经坐标变换后计算出电磁有功功率，同时采集转子角速度，将这两个量在MATLAB-Function模型中运算，即产生控制指令。这样就可以实现风力机的最大功率点跟踪，以及整个系统的有功，无功功率的调节。

3 实验研究

采用Matlab/Simulink软件对基于矢量变换控制的双馈型变速恒频风力发电机的新型登山搜索法的最大功率捕获策略进行仿真。设定双馈异步发动机参数：额定功率5 kW，额定电压380 V，电网频率50 Hz，极对数为2，定子绕组电阻1.865 5，转子绕组电阻2.672 1 Ω，定子漏感0.253 6 H，转子漏感0.253 6 H，定转子互感0.226 9 H，转动惯量0.2 kg·m2；风力机参数：空气密度 1.25 kg/m3，叶轮直径6.64 m，齿轮箱增速比7.923，最佳叶尖速比8.75，最佳风能利用系数0.378。

图4 整个系统的控制策略框图Fig.4 Block diagram of the whole control system

仿真条件为：风速在5 s前为6.5 m/s，5 s时突变为7 m/s，10 s时又突变为7.5 m/s；无功功率给定为600 var。仿真结果如图5～图11所示。

仿真结果（图5、图6、图9）与根据风力机参数计算结果的对比如表1所示。由表1可见，仿真结果都稍稍小于计算结果，但误差很小，基本一致，可以很好地进行最大功率追踪。

图5 给定风速曲线Fig.5 Wind speed curve

图6 风轮转速曲线Fig.6 Rotor speed curve

图7 风轮叶尖速比曲线Fig.7 Tip speed ratio curve

图8 风能利用系数曲线Fig.8 Wind energy utilization coefficient curve

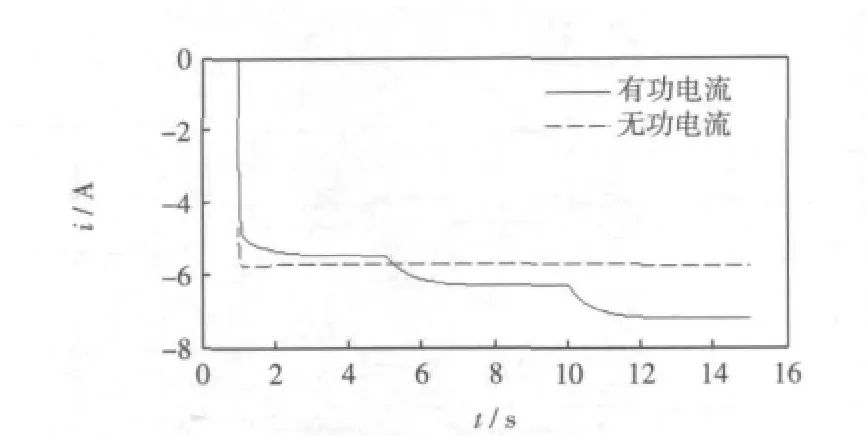
图10 转子有功无功电流曲线Fig.10 Rotor active and reactive current curve

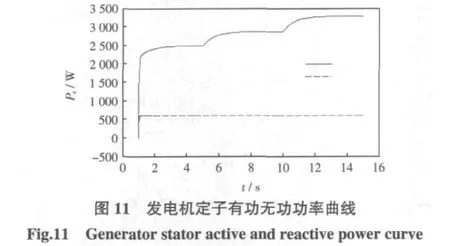
表1 计算与仿真结果对比Tab.1 Calculation compared with the simulation results

图7为风轮叶尖速比曲线，基本接近λopt=8.75，图8为风能利用系数曲线，Cp基本保持0.378。图10为转子侧的有功电流和无功电流曲线，有功电流随着风速的变大而变大，因为风速越大，发电机发出的有功功率就越大，这就需要给转子提供更大的励磁电流；无功电流保持不变，是因为给定的无功功率不变。图11为电机定子侧输出的有功功率和无功功率，有功功率的变化不影响无功功率的变化，很好的实现了有功无功的解耦控制。

4 结语

本文将传统的HCS控方法进行改进，把控制器的输入参数由风机输出的机械功率，转换为发电机输出的电磁功率，并与基于定子磁链定向的矢量控制相结合，设计整个系统的控制策略，采用Matlab/Simulink软件对其进行仿真，得出该方法跟踪速度快，准确度高，而且不需要风机参数，不需要实时测量风速的环节，减少了设备及维护成本，系统自适应能力强，具有很好的鲁棒性。仿真结果验证了该方法的有效性和可行性。

[1]凌禹，张同庄（Ling Yu，Zhang Tongzhuang）.变速风力发电系统控制技术综述（Summary of control algorithms for variable-speed wind-power generation）[J].电力自动化设备 （Electric Power Automation Equipment），2008，28（3）：122-125.

[2]杜志伟，赵峰，田铭兴，等（Du Zhiwei，Zhao Feng，Tian Mingxing，et al）.变速恒频风力发电的最大功率捕获控制研究（Investigation on tracking maximum power point in VSCF wind-power generation system）[J].电气传动（Electric Drive），2007，37（3）：7-10.

[3]邓禹，邹旭东，康勇，等（Deng Yu，Zou Xudong，Kang Yong，et al）.变速恒频双馈风力发电系统最优风能捕获控制（Optimal wind energy capturing control for variable-speed constant-frequency doubly-fed wind power generation system）[J].通信电源技术（Telecom Power Technologies），2005，22（3）：21-24，31.

[4]刘其辉，贺益康，赵仁德（Liu Qihui，He Yikang，Zhao Rende）.变速恒频风力发电系统最大风能追踪控制（The maximal wind-energy tracking control of a variablespeed constant-frequency wind-power generation system）[J].电力系统自动化（Automation of Electric Power Systems），2003，27（20）：62-67.

[5]Teodorescu R，Blaabjerg F.Flexible control of small wind turbines with grid failure detection operating in standalone and grid-connected mode[J].IEEE Trans on Power Electronics，2004，19（5）：1323-1332.

[6]Esmaili R，Xu L，Nichols D K.A new control method of permanent magnet generator for maximum power tracking in wind turbine application[C]//IEEE Power Engineering Society General Meeting，San Francisco，USA：2005.

[7]吴政球，干磊，曾议，等（Wu Zhengqiu，Gan Lei，Zeng Yi，et al）.风力发电最大风能追踪综述（Summary of tracking the largest wind energy for wind power generation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（4）：88-93.

[8]Kojabadi H M，Liuchen Chang，Boutot T.Development of a novel wind turbine simulator for wind energy conversion systems using an inverter-controlled induction motor[J].IEEE Trans on Energy Conversion，2004，19 （3）：547-552.