基于自适应模糊神经网络的风速软测量

董海鹰，魏占宏，杨 玺，李晓青

（兰州交通大学自动化与电气工程学院，兰州 730070）

风速的研究是风力发电系统的重要组成部分，尤其对于大型的风力发电系统的研究具有重要的现实意义。风力发电中风速影响其输出功率，风速是重要参数，因此获得精确风速，更安全有效地控制风力发电机组运行是本文研究的意义所在。目前在许多风力发电机组控制系统中，根据位于机舱顶部的风速计测得的风速调节风力发电机组的输出功率。由于风力发电机组的的动态性能受多种因素的影响，随着时间的推移和工作环境的变化，机组特性会发生变化，为此应采取相应的软测量模型校正措施。在实践上可以通过软件实现或者神经网络芯片将有效风速软测量实际应用于风力发电机组的控制系统中，作为风速计的冗余，使风电机组安全、可靠的运行。

为了解决此问题，软测量技术得到了飞速发展。软测量技术就是依据可测、易测的过程变量（称为辅助变量）与难以直接测量的待测变量（称为主导变量）之间的数学关系，根据某种最优准则，采用各种计算方法，用软件实现对待测量的估计或者测量。文献[1]是针对神经网络算法在软测量建模中的研究，文献[2]将软测量方法用于风速的测量中，把风力发电并网系统当做风速仪对风速进行估计，并建立了风速预测模型。文献[3]是基于支持向量机的风速软测量，文献[4]是基于最小二乘支持向量机的风速软测量，文献[3]和文献[4]都是把风力发电机组当做风速仪，并建立了支持向量机的风速软测量模型，而由于支持向量机模型训练样本时，参数选择需要交叉验证，所以训练的计算量是非常大的。文献[5]是基于神经网络的风速软测量，其有效风速软测量的基本思想是把风力发电系统当做风速仪，建立基于神经网络的风速软测量模型，虽然神经网络具有很强的映射能力和自学习能力，但其收敛速度比较慢，且易陷入局部最小值问题。而自适应模糊神经网络是模糊系统和神经网络相结合，即保留了神经网络的优点，又可以采用模糊规则来确定神经网络结构，更好地优化权值和阈值。

本文将风力发电系统的有效风速估计作为软测量中的主导变量，提出了基于自适应模糊神经网络的风速软测量模型。仿真结果表明基于自适应模糊神经网络的风速软测量模型能很好的跟踪风速的变化趋势，具有很好的精度。

1 软测量的原理

1.1 软测量辅助变量选择

软测量的目的是利用所有易于获取的可测信息，通过计算实现对被测变量的估计。其中可利用的信息包括：可测量的输入，可测主导变量和可测辅助变量。辅助变量的选择分为数量、类型和测点位置的选择。变量数量的选择和过程的自由度、测量噪声和模型的不确定性等有关。其下限值为被估计主导变量的个数。

1.2 软测量的数据处理

软测量是通过过程测量数据经过数值计算而实现的。输入数据预处理包括数据变换和误差处理两方面。数据处理对模型的精度、非线性映射能力都有重要作用。误差处理是保证输入数据准确、有效的必要手段。误差可分为随机误差和过失误差，随机误差是由于随机因素的影响而产生，一般不可避免，但符合一定的统计规律，可采用数字滤波方法来消除。过失误差会极大地影响软测量的在线精度，为此及时剔除和校正这类数据是十分必要的，常用的方法有随机搜索法、神经网络等。

1.3 软测量的模型建立

软测量的原理是利用主导变量和辅助变量的数学关系，通过软件计算得到主导变量的测量值。软测量技术建模的实质就是建立主导变量和辅助变量的数学关系模型。

现在，软测量建模的主要方法有：①机理建模；②回归分析建模；③基于状态估计的模型；④模糊建模；⑤基于机器学习理论的建模；⑥混合建模[6-9]。

1.4 软测量的在线校正

由于过程的时变性、复杂性和测量噪声干扰等影响，控制对象的特性会发生变化。软测量技术在使用过程中，在线校正是至关重要的。必须依据特性的变化及时修正软测量模型来适应过程的变化。

2 基于自适应模糊神经网络的风速软测量

2.1 自适应T-S模糊神经网络

T-S模糊神经模型采用系统状态变量或者属于变量的函数为IF-THEN模糊规则的后件，不仅可以用来描述模糊控制器，也可以描述被控对象的动态模型[11，12]。T-S模糊神经系统是一种自适应能力很强的模糊系统，该系统不仅能自动更新，而且能不断修正模糊子集的隶属函数。T-S模糊神经系统用IF-THEN规则的形式来定义，在规则中为Ri的情况下，模糊推理为

将各隶属度函数进行模糊计算，采用模糊算子为连乘算子。

根据模糊计算结果计算模糊模型的输出值为

T-S模糊神经系统模型对风速软测量这样的复杂系统的建模和测量提供了有效的工具。

2.2 自适应模糊神经网络风速软测量建模

T-S模糊神经网络分为输入层、模糊化层、模糊规则计算层和输出层四层。输入层用输入向量xi连接，节点数与输入向量的维数相同。模糊化层采用隶属度函数式（1）对输入值进行模糊化得到模糊隶属度值，模糊规则计算层采用模糊连乘式（2）计算得到ω，输出层采用式（3）计算模糊神经网络的输出。

有效风速软测量的输入分别为风力机的转速n、发电机的功率P和桨距角β，主导变量为有效风速v*。有效风速的模型可以表示为n、P以及β的非线性函数，即

模糊神经网络风速软测量模型基本结构图如图1所示。

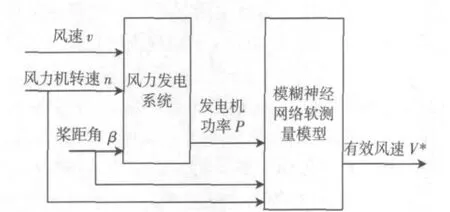
图1 自适应模糊神经网络软测量结构Fig.1 Structure of adaptive fuzzy neural network soft sensor

在所建立的基于模糊神经网络风速软测量模型中，v为风速仪输出的大采样间隔的测量值，它是用于离线辨识模型的参数，也是用于软测量模型的在线自校正；可测变量风力机转速n、控制输入桨距角β以及可测变量发电机功率P都是软测量模型的输入变量，被估计变量的最优估计有效风速v*为输出，用模糊神经网络实现输入输出的非线性函数关系。在该风速软测量中模糊神经网络在本质上就是将常规神经网络赋予模糊输入信号和模糊权值。所以建立模糊神经网络软测量模型结构如图2所示。

在图2中网络对应的输入输出映射关系如下。

输入层输入节点为

式中：xi表示网络的输入。

模糊化层输入节点为

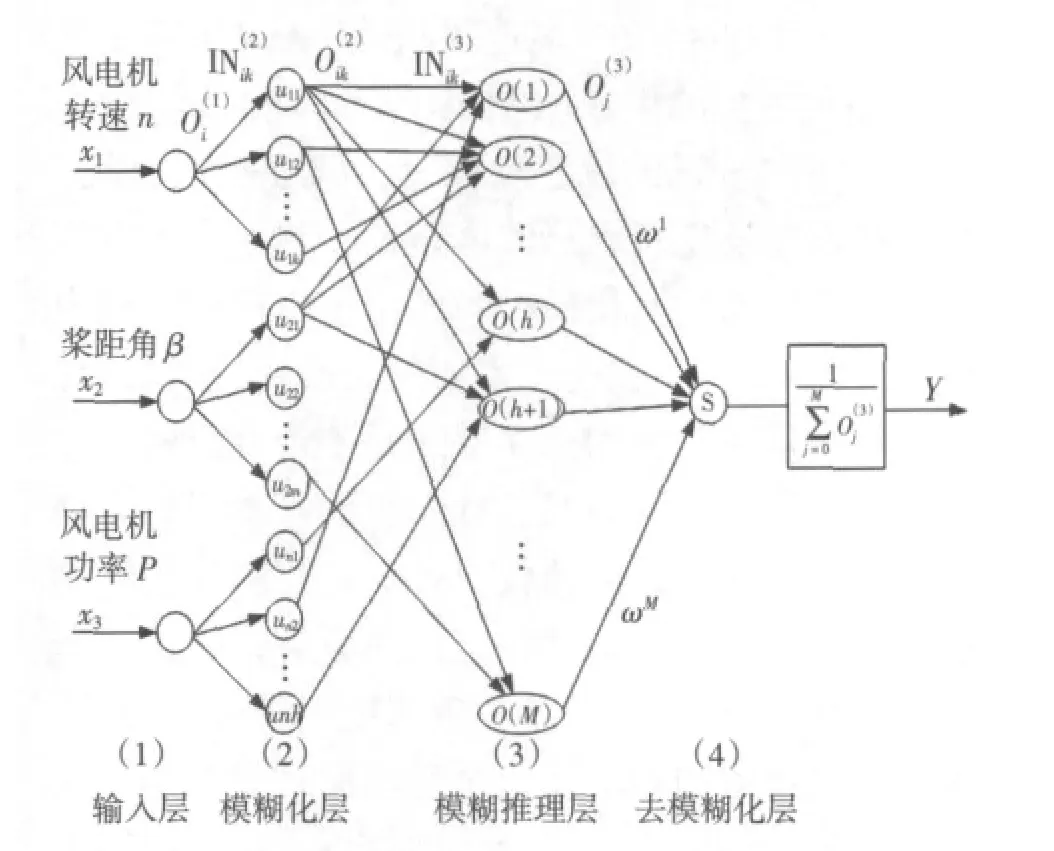
图2 模糊神经网络软测量模型Fig.2 Soft sensor model of fuzzy neural network

输出节点为

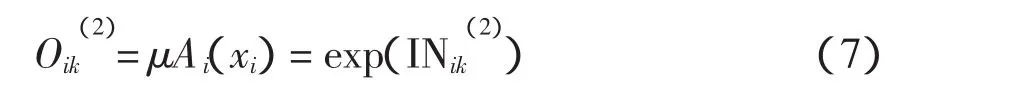
模糊推理层输入节点为

输出节点为

去模糊化层输入节点为

输出节点为

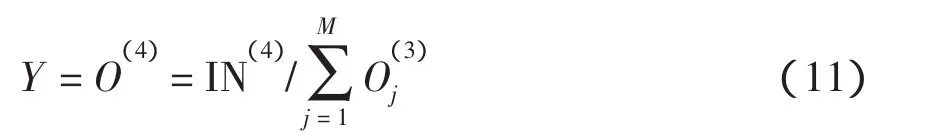
模糊神经网络的学习算法如下。

（1）误差计算为

式中：yd是网络期望输出；yc是网络实际输出；e为期望输出和实际输出地误差。

（2）系统修正为

参数修正公式为

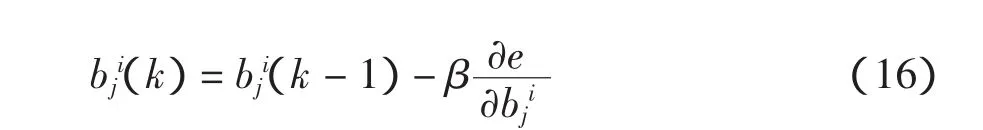
2.3 基于模糊神经网络的软测量建模步骤

（1）确定采集样本的输入输出变量，输入变量分别是风力机的转速n、发电机的功率P和桨距角β，输出变量为有效风速v*。

（2）以风电场的实测数据作为样本数据，对样本数据进行校验和标准化变化。

（3）对样本优化组合，进行模糊神经网络训练。

（4）用确认集进行检验，提取模糊神经网络的各个参数建立T-S模糊神经网络模型。

2.4 基于自适应的模糊神经网络风速软测量算法流程

基于T-S模糊神经网络风速软测量算法流程见图3。其中，模糊神经网络构建根据训练样本维数确定模糊神经网络输入/输出节点数、模糊隶属度函数个数，由于输入数据为3维，输出数据为1维，所以模糊神经网络结构为3-6-1，即输入层有3个节点，隐含层有6个节点，也即有6个隶属度函数，输出层有1个节点，选择4组系数p0～p3，模糊隶属度函数中心和宽度c和b随机得到，网络学习速率α采用变学习率方法得到，动量学习率β为0.5，迭代次数为100次，利用Matlab编写.m文件实现自适应模糊神经网络风速软测量仿真。

选用参数说明：网络的隐含层节点数对网络精度有较大的影响：节点数太少，网络不能很好地学习，需要增加训练次数，训练的精度也受影响；节点数太多，训练时间增加，网络容易过拟合。最佳隐含层节点数选择可参考公式

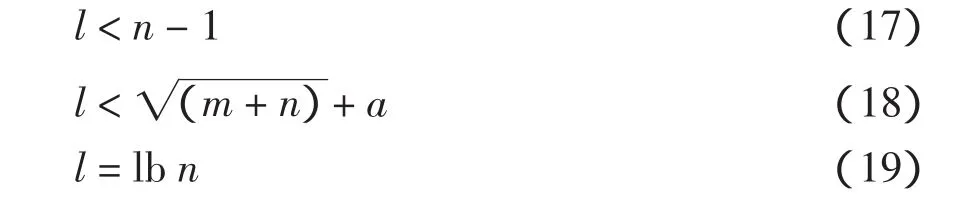
式中：n为输入层节点数；l为隐含层节点数；m为输出层节点数；a为0～10之间的常数。在实际问题中，隐含层节点数的选择首先是参考公式来确定节点数的大概范围，然后用试凑法确定最佳的节点数，针对此网络结构试凑得出a=5。

网络学习率α的取值在[0，1]之间，学习率α越大，对权值的修改越大，网络学习速度越快；但过大的学习率将使权值学习过程中产生震荡，过小的学习率使网络收敛过慢，权值难以趋于稳定。本文采用变学习率方案，令学习率α随着学习的进展而逐步减小，可收到较好的效果。变学习率为

式中：αmax为最大学习率；αmin为最小学习率；tmax为最大迭代次数；t为当前迭代次数。

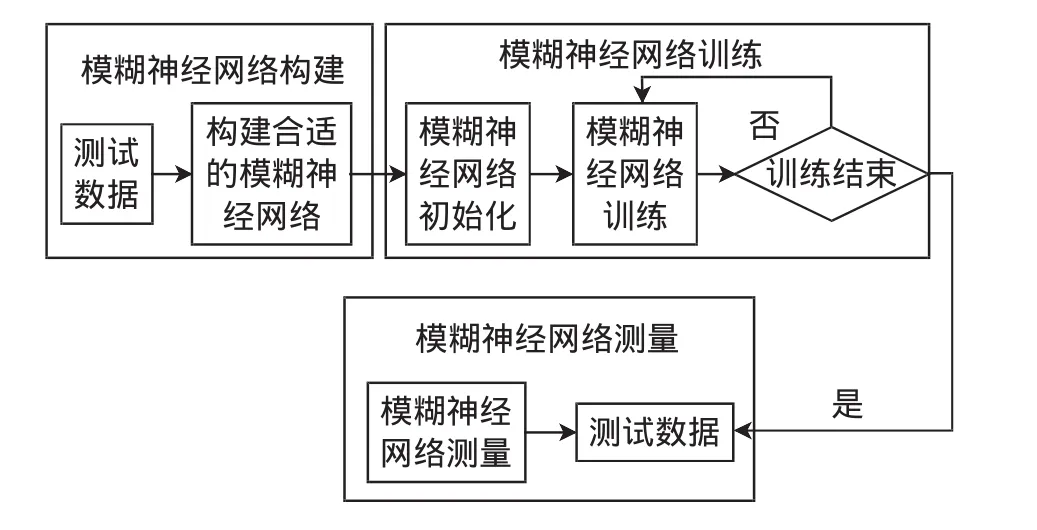
图3 模糊神经网络风速软测量算法流程Fig.3 Algorithm flow chart of fuzzy neural network wind speed soft sensor

模糊神经网络训练用训练数据训练模糊神经网络，网络反复训练100次。模糊神经网络测量用训练好的模糊神经网络测量风速。

3 基于自适应模糊神经网络的风速软测量仿真实验

本文采用内蒙古某风电场2009年3月1日到10日样本数据，采用每10 min记录一次，共1 440组样本，从中选取1 296组作为网络训练数据，剩余144组数据作为网络测试数据，样本数据是从1.5 MW双馈异步风力发电机组获得的，该样本采集数据从切入风速4 m/s到高于25 m/s时发电机组自动刹车为止。采集的数据包括风速v，风力发电机组转速n、桨距角β和发电机输出功率P，首先将变量样本中经过显著误差剔除和滤波处理后得到一个样本集，然后再利用处理后的参数变量建立风速的软测量样本集。风力发电机的参数如表1所示。

基于自适应模糊神经网络风速软测量仿真和自适应模糊神经网络风速误差如图4和图5所示。

不同时间段对应的自适应模糊神经网络风速误差值如表2所示。

由表2中可以看出：风速估计值和风速样本值基本吻合；由基于自适应模糊神经网络风速仿真图中可以看出：风速估计值很好地跟踪了风速样本值；测量误差中最大的误差为0.212 4 m/s。

为了进行对比，利用神经网络对有效风速进行了估计。基于神经网络风速软测量仿真和神经网络风速误差如图6和图7所示。

表1 风力发电机的参数Tab.1 Parameters of wind turbine generator

图4 自适应模糊神经网络风速仿真Fig.4 Wind speed simulation of adaptive fuzzy neural network

图5 自适应模糊神经网络风速误差Fig.5 Wind speed error simulation of adaptive fuzzy neural network

不同时间段对应神经网络风速误差见表3。

在相同的有效风速训练样本下，使用了神经网络进行有效风速的估计，通过表2和表3比较可以看出：自适应T-S模糊神经网络训练的风速估计值的最大误差为0.204 2 m/s，而神经网络训练有效风速估计的最大误差为0.391 6 m/s；从神经网络风速仿真中可以看出：风速估计值和风速样本值的误差相对较大；仿真中测量误差中最大的误差为0.462 4 m/s。仿真结果表明了基于模糊神经网络的软测量能够高精度地估计出风力发电系统的有效风速。

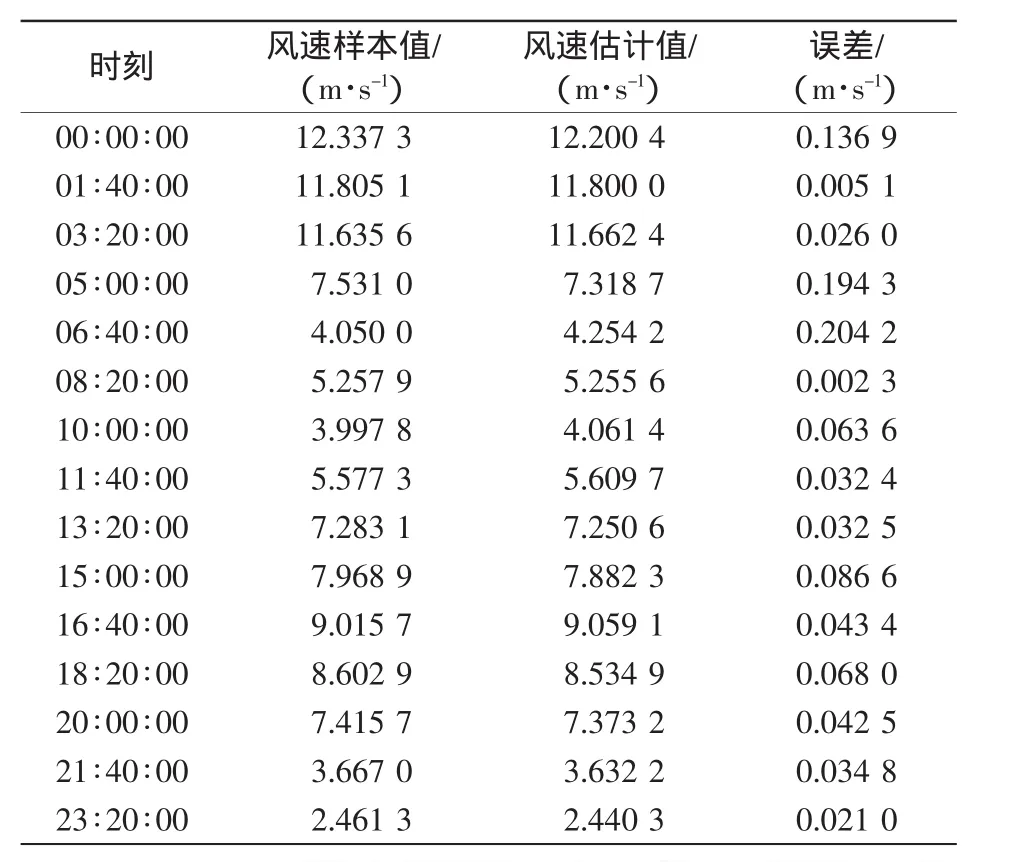
表2 不同时间段对应的误差值（Ⅰ）Tab.2 Error values corresponding to different time periods（Ⅰ）

图6 神经网络风速仿真Fig.6 Wind speed simulation of neural network

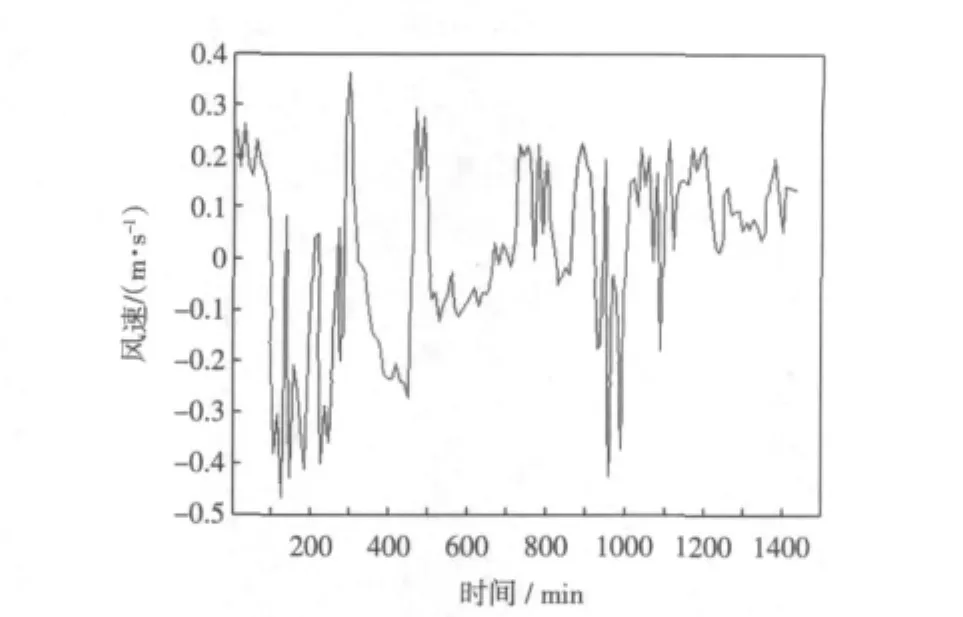
图7 神经网络风速误差值Fig.7 Wind speed error simulation of neural network

表3 不同时间段对应的误差值（Ⅱ）Tab.3 Error values corresponding to different time periods（Ⅱ）

4 结语

本文利用模糊控制和神经网络优势互补的特点，建立模糊控制和神经网络相结合的自适应T-S模糊神经网络对风速模型进行分析研究，并进行了仿真实验。仿真结果表明，风速估计值很好地跟踪了风速样本值，不仅可以加快收敛速度和改善局部收敛性，而且具有学习能力强和泛化能力好等优点。证明了基于自适应T-S模糊神经网络的软测量对于大范围的风速变化时，能够很好地跟踪风速的变化趋势，是一种有效的风速测量方法。

[1]郭庆武，张湜，林锦国（Guo Qingwu，Zhang Shi，Lin Jinguo）.Matlab神经网络工具箱及其在软测量建模中的应用（Neural network toolbox in Matlab and its application in building soft-sensing models）[J].东南大学学报：自然科学版 （Journal of Southeast University：Natural Science Edition），2003，33（S1）：209-212.

[2]Leith D J，Leithead W E.Application of nonlinear control to a HAWT[C]//3rd IEEE Conference on Control Applications，Glasgow，UK：1994.

[3]张新房，徐大平，柳亦兵，等（Zhang Xinfang，Xu Daping，Liu Yibing，et al）.大型变速风力发电机组的风速软测量（Wind speed soft sensor for large-scale variable speed wind turbines）[J].太阳能学报（Acta Energiae Solaris Sinica），2006，27（4）：321-325.

[4]纪国锐，董泽，韩璞，等（Ji Guorui，Dong Ze，Han Pu，et al）.基于最小二乘支持向量机的风力发电机组风速软测量（Wind speed soft sensor for wind turbines based on least square SVM）[J].中国电力（Electric Power），2009，42（2）：75-78.

[5]刘震，汪令祥（Liu Zhen，Wang Lingxiang）.基于神经网络的风力发电系统风速软测量（Study on wind speed soft sensing based on neural networks for wind power generators）[J].中国电力（Electric Power），2010，43（11）：87-91.

[6]潘立登，李大宇，马俊英.软测量技术原理与应用[M].北京：中国电力出版社，2009.

[7]吴燕玲，卢建刚，孙优贤（Wu Yanling，Lu Jiangang，Sun Youxian）.基于多目标遗传规划的软测量建模方法（Soft sensor modeling based on multi-objective genetic programming）[J].传感技术学报（Chinese Journal of Sensors and Actuators），2007，20（9）：2029-2034.

[8]韩璞，乔弘，王东风，等（Han Pu，Qiao Hong，Wang Dongfeng，et al）.火电厂热工参数软测量技术的发展和现状（Development and current status of thermal parameter soft-sensing technique in power plant）[J].仪器仪表学报 （Chinese Journal of Scientific Instrument），2007，28（6）：1139-1146.

[9]Gonzalez G D，Redard J P，Barrera R，et al.Issues in softsensor applications in industrial plants[C]//IEEE International Symposium on Industrial Electronics.Santiago，Chile：1994.

[10]Han Min，Sun Yannan，Fan Yingnan.An improved fuzzy neural network based on T-S model[J].Expert Systems with Applications，2008，34（4）：2905-2920.

[11]Horikawa Shin-ichi，Furuhashi Takeshi，Uchikawa Yoshiki.On fuzzy modeling using fuzzy neural networks with the back-propagation algorithm [J].IEEE Trans on Neural Networks，1992，3（5）：801-806.

[12]Zhang J，Morris A J.Fuzzy neural networks for nonlinear systems modelling[J].IEEE Proceedings-Control Theory and Applications，1995，142（6）：551-561.

[13]陈国初，杨维，张延迟，等（Chen Guochu，Yang Wei，Zhang Yanchi，et al）.风电场风速概率分布参数计算新方法（New computation method of wind speed probability distribution parameters in wind farm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：46-51.