交直流输电系统低频振荡仿真分析

史华勃，刘天琪，李兴源

（四川大学电气信息学院，成都 610065）

区域电网互联形成大规模电力系统可实现能源资源优化配置、电网错峰、故障情况下紧急功率支援等功能。然而，随着电网互联规模日益扩大，带来诸多优点的同时，电网互联所引发的低频振荡事故时有发生，已成为威胁电网安全运行、制约电网传输能力的最主要问题之一[1]。

低频振荡作为电力系统的重要问题之一，得到了广泛的研究[2-5]。人们对弱阻尼振荡、强迫振荡、分叉理论、混沌理论、强共振机理等进行了研究[6]。其中，弱阻尼振荡最为成熟，强迫振荡[7-11]成功解释了实际系统中弱阻尼振荡无法解释的低频振荡现象[7]。其他机理中，有些在理论上还没有得到很好的解决，有些还停留在理论上的探讨，工程上难以应用。采用弱阻尼振荡和强迫振荡解释电力系统低频振荡，在工程应用上具用重要意义。近年来，高压直流输电[12-14]在远距离、大容量的区域互联中得到了广泛的应用。高压直流输电具有输送容量大、距离远，线路损耗小、调节速度快等优点，但是直流的接入也会对系统低频振荡模式产生一些影响。

本文针对以下几点对交直流输电系统中的低频振荡进行了分析比较：①弱阻尼振荡和强迫振荡现象、机理的异同和影响因素；②直流输电对低频振荡机电和非机电模式的影响；③强迫振荡与弱阻尼振荡在交直流输电系统中的表现形式和对电力系统的危害。分析结果有利于低频振荡的解释、监测和控制，对电力系统安全稳定运行具有重要意义。

1 弱阻尼振荡与强迫振荡机理

弱阻尼振荡与强迫振荡，两种振荡发生机理不同；起振后，表现形式也不同。对单机无穷大系统而言，线性化发电机转子运动方程为

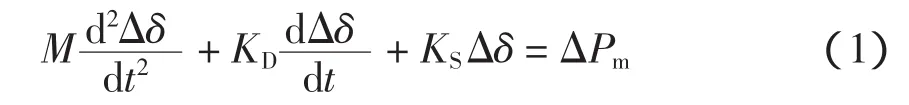
式中：M为转子惯性常数；KD为阻尼系数；KS为同步转矩系数；Δδ为转子角偏移；ΔPm为原动机功率变化量。

当忽略原动机功率变化，即ΔPm为0时，转子运动方程变为二阶常系数齐次微分方程

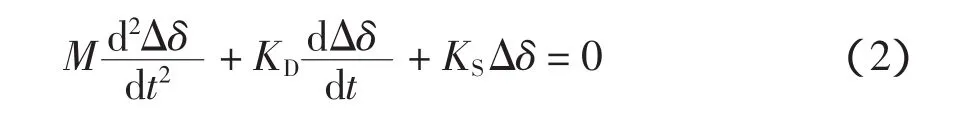
式（2）即是采用弱阻尼振荡机理分析电力系统低频振荡所用的转子运动方程，其特征值为

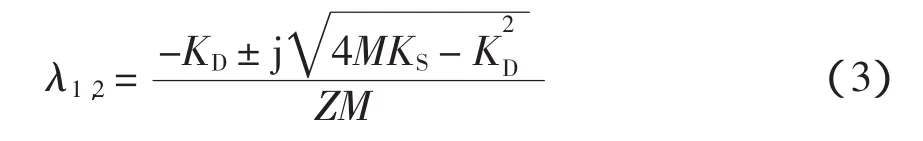
当特征值实部小于零，即是正阻尼时，扰动后系统呈衰减振荡，阻尼越弱衰减越慢；当特征值实部大于零时，即呈现负阻尼时，扰动后系统将呈增幅振荡；当阻尼为0时，出现等幅振荡。

当原动机功率不能忽略，出现周期性小扰动时，令

式中：A为扰动幅值；ω为扰动频率。则运动方程变为

考虑强迫振荡时所用的转子运动方程，为二阶常系数非齐次微分方程，其通解Δδ1（t）为一衰减振荡，随时间变化最终只剩下特解Δδ2（t）。

发电机快速励磁系统、重负荷、网络结构、运行方式变化等都可能使系统的固有阻尼减小。当特征值实部由负变正，阻尼为负时，扰动后转子增幅振荡；阻尼为正时振荡逐渐衰减。当系统持续性周期小扰动信号频率与系统固有频率一致或接近时将发生强迫振荡。其振荡频率与扰动频率相同，其振幅与扰动幅值、发电机阻尼系数、发电机转动惯量等因素有关。强迫振荡发展过程除与上述因素相关外，还与式（6）所示的通解随时间的衰减情况密切相关。

式中，B、φ分别为强迫振荡的幅值、相位。

2 交直流输电系统低频振荡

影响系统低频振荡模式的因素较多，除了发电机组快速励磁、电网运行方式等，随着高压直流输电在电网互联中的广泛应用，也带来了一些问题。

对交流系统来说，高压直流换流站相当于一个对频率不敏感的负荷，它对系统摇摆将产生负阻尼；不论对弱阻尼振荡还是强迫振荡都将产生不利影响，会削弱互联系统稳定性。直流系统运行工况也可能影响低频振荡，如直流传输功率大小。

此外，直流输电系统的基本被控量是直流电流，一般由整流侧控制电流而逆变侧保持电压。这种控制方式虽然可以缓冲一侧交流系统对另一侧交流系统的扰动，但是由于换流站隔离了两端交流系统，使其联系减弱，不能流过同步功率，减小了电力系统同步转矩，对系统稳定也将产生不利影响。

系统自由运动，对应零输入时的状态方程[15]为

式中：φ为A的模态矩阵；A为系统状态矩阵；Z为状态变量。

由系统状态方程可求得用于度量状态变量和振荡模式之间的关联程度的参与矩阵P。

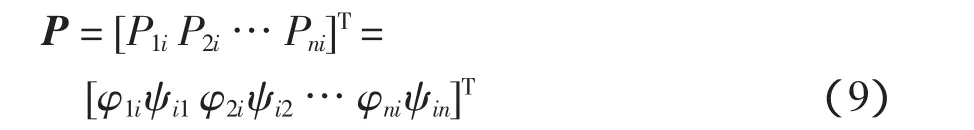
式中：φni为右特征向量 φi的第 n项；ψin为左特征向量ψi的第n项。参与矩阵P的元素Pni=φniψin为参与因子，它度量了第i个模式与第n个状态变量的相互参与程度。

研究发现，持续性周期小扰动所引发的各机组强迫振荡幅值也与参与因子有较大关系，参与因子较大的发电机组强迫扰动幅值更大。当扰动频率与本地振荡模式频率接近时将引发局部强迫振荡，而未参与此振荡模式的机组基本不受影响。当扰动频率与区域间振荡模式频率接近时，将引发全局性强迫振荡，振荡幅值仍然按各发电机组参与因子从大到小依次降低。此外，由于受发电机组参与因子的影响，扰动源位于参与因子大的机组时强迫振荡更严重。

3 多机交直流系统低频振荡的仿真分析

以上关于弱阻尼振荡和强迫振荡的分析虽然是针对单机系统，为验证其结论同样适用于多机系统，对多机系统算例进行仿真分析。

3.1 仿真算例

采用如图1所示的交直流并联两区域系统研究交直流输电系统低频振荡。其中，包含一条额定功率200 MW的直流输电线，两条交流线路。每个区域各有两台额定容量900 MVA的机组。发电机采用包含励磁的5阶模型，有功负荷具有恒电流特性，无功负荷具有恒阻抗特性。详细发电机参数，励磁系统参数、负荷参数、直流输电系统参数、交流输电线路参数可参考文献[15]。

因为BPA软件不能在原动机输入转矩上施加周期性小扰动信号，所以在BPA计算平台上建立仿真模型，以计算多机系统的特征值；在PSCAD平台上建立参数一致的相应模型，以便进行强迫振荡及弱阻尼振荡的仿真分析。

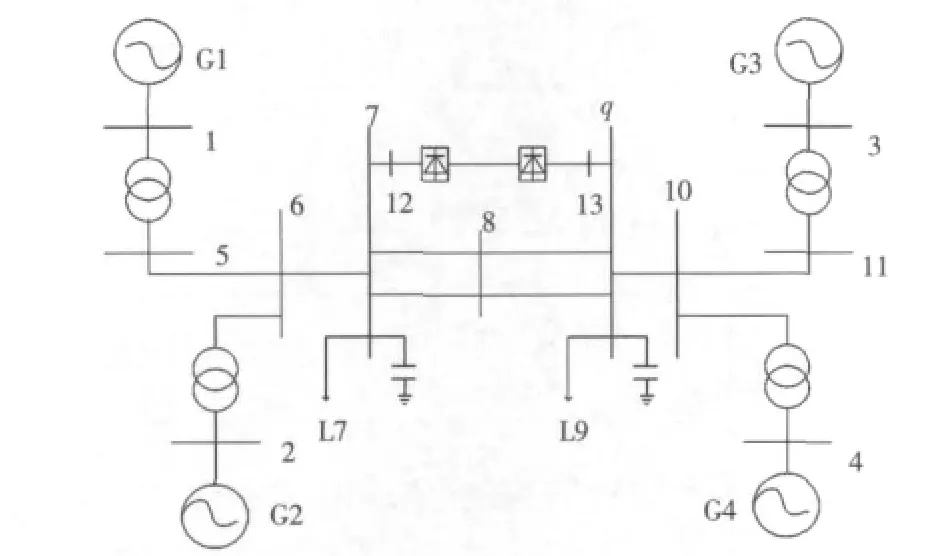
图1 交直流并联两区域系统Fig.1 Two-area system with paralleled DC and AC lines

3.2 直流输电对系统低频振荡的影响

根据系统状态方程可解出大量的特征值，但是，根据机电回路相关比[4]选出与变量Δω和Δδ强相关的特征值（机电模式），只有这些强相关的特征值才可能是低频振荡对应的根，其余则为非机电模式。为研究直流输电对系统低频模式的影响，首先断开图1所示的两区域系统中的直流联络线，使其成为一个只含交流联络线的系统，计算求得41个特征值；根据相关比选出对低频振荡影响较大的11个特征值，如表1所示。

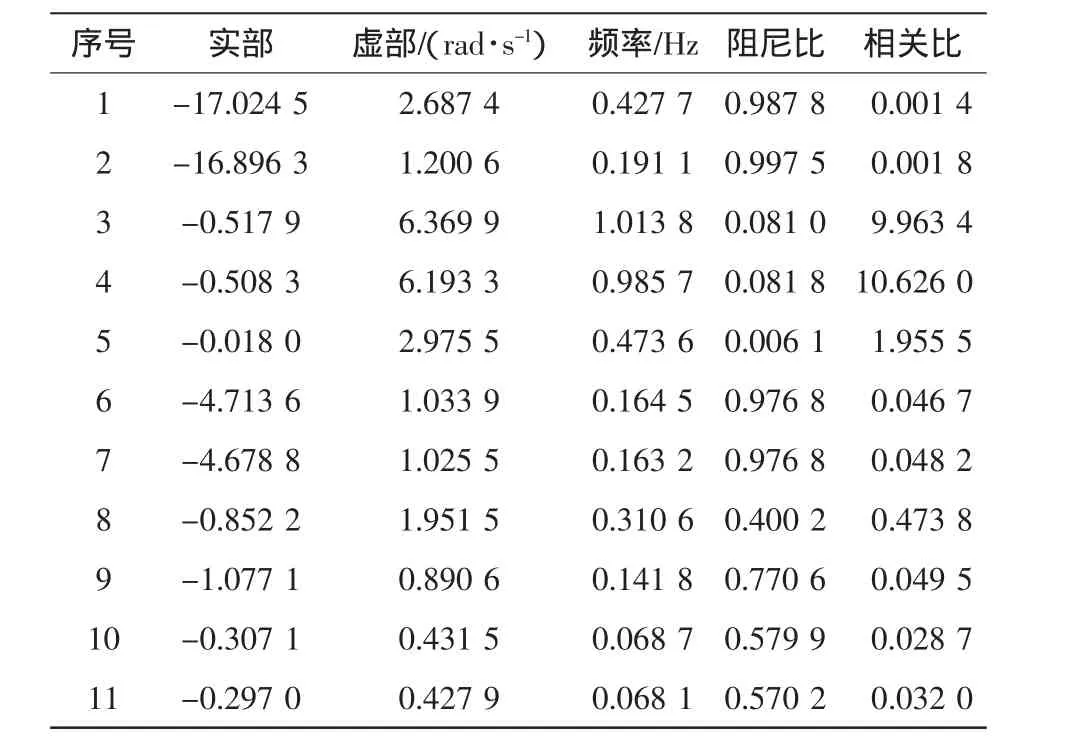
表1 交流两区域系统部分特征值Tab.1 Partial eigenvalues of two-aera AC system

其中包含3个机电回路相关比大于1的机电振荡模式，模式5为发电机G1、G2相对于G3、G4的区域间振荡，模式4和模式3分别为G1和G2之间、G3和G4之间的局部振荡。其余为非机电振荡模式。

对交直流并联两区域系统同样选出11个特征值，如表2所示。对比表1和表2可以看出：接入直流输电线路后，系统机电振荡模式中，只有模式4的阻尼略有增加，其余模式阻尼全部减小，非机电振荡模式的阻尼除模式6和模式7不变外，其余全部减小；各模式振荡频率，部分升高、部分降低。由此说明，高压直流输电在大区电网互联中虽然具有诸多优势，但可能会使系统的阻尼减小，对弱阻尼振荡、强迫振荡都不利，会降低系统的稳定性，对阻尼较弱系统应特别注意。

直流系统参数中，直流功率水平对低频模式影响较大。图 2 中，（a）、（b）分别为图 1 所示交直流并联两区域系统机电和非机电模式特征值随功率水平变化趋势。图2中横坐标为衰减因子，即特征值实部；纵坐标为频率，即特征值虚部。

图2（a）表明：随着直流功率水平的增加，机电振荡模式特征值逐渐向复平面右方移动，阻尼逐渐减小，而振荡频率基本不变。

图2（b）表明：随着直流功率水平的增加，非机电振荡模式特征值变化并不明显，阻尼基本不变，有些模式频率略有升高，其余基本不变。

一般，通过直流功率调制可以增加阻尼。但是，当直流调制已经不能很好解决系统稳定问题时，适当降低直流功率水平有助于增加机电振荡模式的阻尼，有利于电力系统的稳定。虽然降低功率水平是以降低电力系统的经济性为代价的，但是对于低频振荡发生后的稳定控制来讲，降功率运行也是值得的。

表2 交直流并联两区域系统部分特征值Tab.2 Partial eigenvalues of two-aera AC/DC system

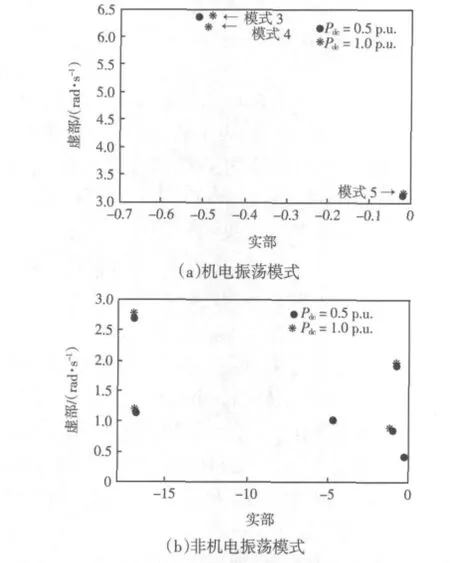
图2 低频模式特征值随直流功率水平变化趋势Fig.2 Eigenvalues change trend with DC power level in low frequency mode

3.3 强迫振荡与弱阻尼振荡表现形式

有文献研究表明：汽轮机压力脉动、水轮机尾水管压力脉动、周期性负荷扰动等呈周期性变化的扰动都可能引发电力系统强迫功率振荡；高速励磁系统、重负荷、区域弱联等都可能引发弱阻尼低频振荡；两种机理低频振荡发生后的表现形式各不相同。

3.3.1 强迫振荡

在表2所示的交直流两区域系统部分特征值中，模式3为发电机G3和G4之间的局部振荡模式，振荡频率1.016 6 Hz，阻尼比0.080 0。其中，G3和G4在本模式的参与因子分别为0.707 5和1.0。

4 s时，在G3机组的输入机械转矩上施加频率为1.016 6 H，幅值0.01p.u.的正弦扰动信号，25 s时切除扰动源，仿真结果如图3（a）所示。此外，在G4机组上也单独施加与G3上相同的扰动信号，仿真结果如图3（b）所示。为了方便分析比较，图3中功率采用标幺值，功率基准值为900 MW。

由图3（a）可知，发电机G3强迫振荡功率峰峰值为36.5MW，G4强迫振荡功率峰峰值为49.6MW。起振时速度较快，到达最大值后呈等幅振荡，扰动源消失后由于阻尼较弱，振荡缓慢衰减。而发电机G1、G2振荡非常小，基本不受此扰动信号的影响。由图3（b）知，G3上振荡功率峰峰值为37.4 MW，G4振荡功率峰峰值为53.14 MW，大于扰动源位于G3时激发的强迫振荡。

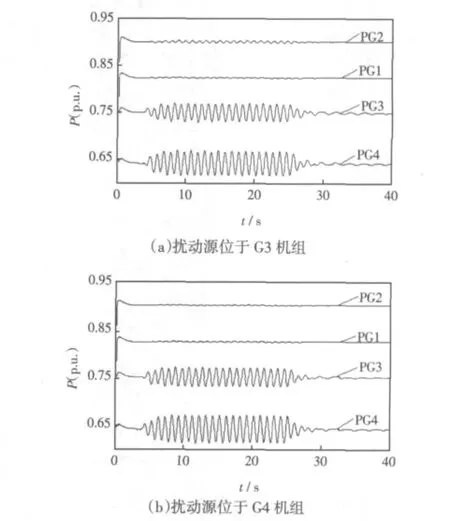
图3 局部强迫振荡时各机组有功出力Fig.3 Power of each generator when local forced oscillation occurs

结果表明即使是非常小的扰动，只要频率接近或者等于系统固有振荡频率都可能在发电机组上激发出较大的强迫功率振荡。振荡发展过程除受扰动信号幅值影响，还受系统阻尼情况以及发电机组的参与因子影响。参与因子越大则扰动激发的强迫振荡功率幅值越大，反之越小。当强迫扰动发生在参与因子越大的机组上，激发出的功率振荡越大。

在表2所示的交直流两区域系统部分特征值中，模式5为发电机G1、G2和G3、G4之间的区域间振荡模式，振荡频率0.505 6 Hz，阻尼比0.003 9。其中，G1、G2、G3、G4 在本模式的参与因子分别为0.486 9、0.264 2、1.0、0.626 4。

4 s时，在G1机组的输入机械转矩上施加频率为0.505 6 Hz，幅值0.01p.u.的正弦扰动信号，25 s时切除扰动源，仿真结果如图4所示。

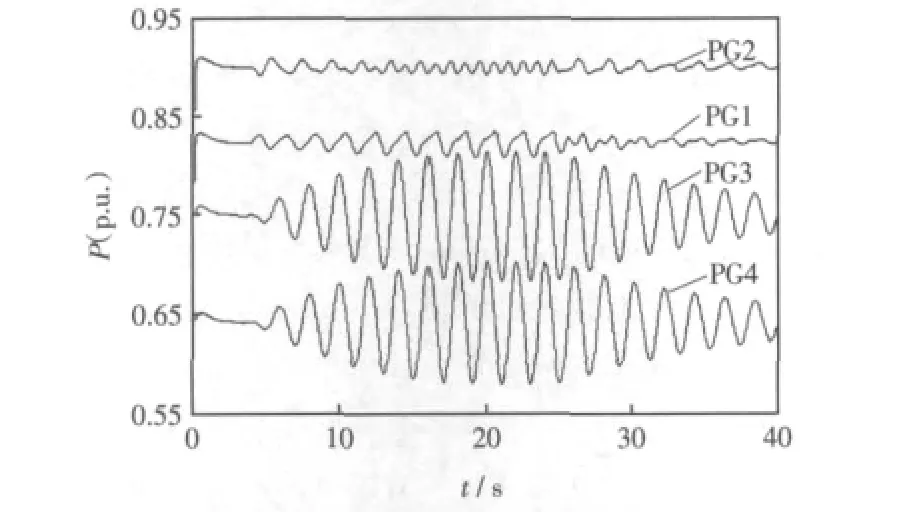
图4 全局性强迫振荡，各机组有功出力Fig.4 Power of each generator when forced oscillation occurs in overall system

由图4可知，发电机组G1上的周期性扰动导致了全局性的强迫振荡。由于本模式振荡频率更低，在较短的仿真时间，较早切除扰动源的情况下并没有看到与图3中相同的明显等幅振荡。在机组上激发的振荡功率峰峰值大小仍然按照机组参与因子的大小而变化。G1强迫振荡峰峰值为23.7 MW，G2强迫振荡峰峰值为15.9 MW，G3强迫振荡峰峰值为118.4 MW，G4强迫振荡峰峰值为110.6 MW。与局部性强迫振荡不同的是，全局强迫振荡除了会在机组上激发较大的功率振荡，还会在联络线上激起较大幅值的功率振荡，如图5所示，其中功率基准值为200 MW。

由图5可知，全局强迫振荡时，在交流联络线上激起了大幅的功率振荡，峰峰值为59.5 MW；在直流联络线上激起的振荡幅值稍小，峰峰值为15.5 MW，交、直流联络线上功率振荡都比局部性振荡时更严重。

由图3～图5可知：周期性的扰动信号激起的全局性强迫振荡比局部性的强迫振荡更具破坏力，不论是发电机组还是交流或者直流联络线上都会激起大幅振荡。这不仅会对发电机组造成危害，还会对联络线造成威胁，轻则跳闸解列，重则造成电力系统大事故。所以，在电力系统运行中，更要注意监测和防范此类强迫振荡。

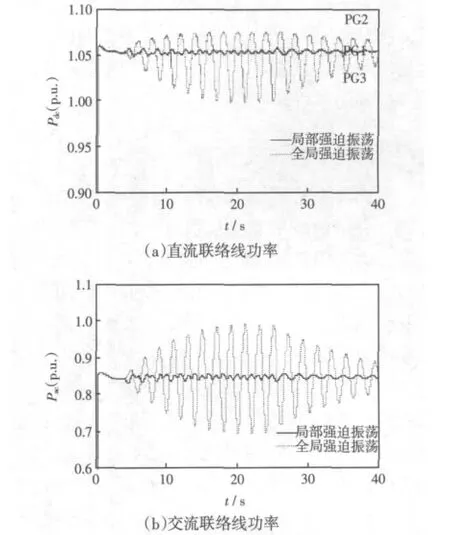
图5 强迫振荡时联络线功率Fig.5 Power of connecting line when forced oscillation occurs

3.3.2 弱阻尼振荡

在图1所示系统中，母线9在4 s时施加一个持续时间83 ms的三相短路故障以激发出低频振荡。图6为瞬时扰动引发低频振荡时，交流联络线功率振荡仿真曲线。发电机组功率振荡幅值仍按参与因子大小排列，此处不再赘述。

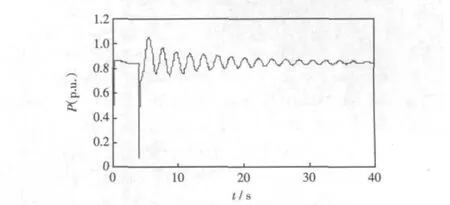
图6 瞬时扰动时交流联络线功率Fig.6 Power of AC line when transient disturbance occurs

由图6可知，由于系统阻尼较弱，瞬时扰动引发低频振荡后，衰减速度相当慢。对比图3中典型强迫振荡波形及理论分析可知，只要扰动源没有消失，强迫振荡就会持续进行，只受扰动源和系统阻尼等因素影响，对系统的危害会有所不同。而强迫振荡发生时一般先以增幅振荡形式，继而发展为等幅振荡（由于扰动可能并非严格按正弦变化，实际强迫振荡可能不是严格等幅振荡），扰动源消失后系统行为则可用弱阻尼振荡机理来分析。

对于强迫振荡发生时最好的解决方法是找到具体扰动源，并切除；对于弱阻尼振荡的解决方法还是应从增加系统阻尼入手，增加系统阻尼皆有利于抑制两种机理低频振荡。

4 结语

本文对交直流输电系统低频振荡现象进行了研究，分析比较了交直流输电系统中弱阻尼振荡和强迫振荡现象、机理的异同和影响因素。采用单机系统分析低频振荡，所得结论同样适用于多机系统，弱阻尼振荡和强迫振荡能够很好地解释电力系统中的低频振荡现象。研究表明：高压直流输电的接入会削弱系统的阻尼，直流功率水平主要影响系统低频振荡机电模式，降功率运行有利于提高系统的稳定性。强迫振荡发生时，机组功率振荡幅值仍按参与因子大小不同而不同。全局性强迫振荡比局部强迫振荡危害更大。对于强迫振荡最好解决方法是发现并切除扰动源，增加系统阻尼都有利于两种低频振荡的抑制，具体抑制措施值得深入研究。

[1]顾丽鸿，周孝信，陶洪铸，等（Gu Lihong，Zhou Xiaoxin，Tao Hongzhu，et al）.局部弱联诱发互联电网强迫振荡机制分析（Analysis on mechanism of inter-area forced oscillation caused by local weak interconnection in interconnected power grid）[J].电网技术（Power System Technology），2010，34（12）：36-43.

[2]DeMello F P，Concordia C.Concept of synchronous machine stability as affected by excitation control[J].IEEE Trans on PAS，1969，88（4）：316-329.

[3]韩松，徐政，何利铨（Han Song，Xu Zheng，He Liquan）.互联电网区间振荡动态特性分析方法述评（Current research review：Dynamic characteristic analysis methods for inter-area oscillations in interconnected power systems）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2011，23（4）：6-14.

[4]倪以信.动态电力系统理论和分析[M].北京：清华大学出版社，2002.

[5]徐政.交直流电力系统动态行为分析[M].北京：机械工业出版社，2004.

[6]王青，闵勇，张毅威（Wang Qing，Min Yong，Zhang Yiwei）.电力系统低频振荡的机理研究和主要分析方法（The mechanism research and main analysis method of low frequency oscillation in power system）[J].电气应用（Electrotechnical Application），2006，25（7）：1-6.

[7]王铁强，贺仁睦，王卫国，等（Wang Tieqiang，He Renmu，Wang Weiguo，et al）.电力系统低频振荡机理的研究（The mechanism study of low frequency oscillation in power system）[J].中国电机工程学报（Proceedings of the CSEE），2002，22（2）：21-25.

[8]汤涌（Tang Yong）.电力系统强迫功率振荡的基础理论（Fundaments theory of forced power oscillation in power system）[J]. 电 网 技 术 （Power System Technology），2006，30（10）：29-33.

[9]韩志勇，贺仁睦，徐衍会（Han Zhiyong，He Renmu，Xu Yanhui）.汽轮机压力脉动引发电力系统低频振荡的共振机理分析（Study on resonance mechanism of power system low frequency oscillation induced by turbo-pressure pulsation）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（1）：47-51.

[10]刘志坚，束洪春，王海军，等（Liu Zhijian，Shu Hongchun，Wang Haijun，et al）.水轮机尾水管压力脉动对电力系统低频振荡的影响（Effect of pressure fluctuation in hydraulic turbine draft tube on low-frequency oscillation of electric power system）[J].水利水电技术（Water Resources and Hydropower Engineering），2009，40（4）：58-61，75.

[11]余一平，闵勇，陈磊，等（Yu Yiping，Min Yong，Chen Lei，et al）.周期性负荷扰动引发强迫功率振荡分析（Analysis of forced power oscillation caused by continuous cyclical load disturbances）[J].电力系统自动化（Automation of Electric Power Systems，），2010，34（6）：7-11.

[12]李兴源.高压直流输电系统[M].北京：科学出版社，2010.

[13]罗隆福，付颖，李勇，等（Luo Longfu，Fu Ying，Li Yong，et al）.直流输电控制器原理及稳态特性分析（Controller of HVDC transmission system and its steady-state performance analysis）[J].电力自动化设备（Electric Power Automation Equipment，），2009，29（1）：65-69.

[14]韩民晓，丁辉，陈修宇，等（Han Minxiao，Ding Hui，Chen Xiuyu，et al）.高压直流输电系统电磁暂态建模（Electromagnetic transient modeling of HVDC system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（4）：7-11.

[15]Kunder P.Power System Stability and Control[M].New York：McGraw-Hill Inc，1994.