矩阵束辨识多直流系统控制敏感点

王 曦，王渝红，李兴源，赵 睿

（四川大学电气信息学院，成都 610065）

电力系统低频振荡是指发电机组转子动能与电网势能之间的持久的机电振荡，随着大电网的互联，发生低频振荡的可能性和造成的危害性日益增加，低频振荡限制联络线输送的功率，并可能导致系统故障后振荡失步[1-3]。抑制低频振荡的主要手段包括在发电机组上安装电力系统稳定器（power system stabilizer，PSS）[4-6]以及利用高压直流输电（high voltage DC，HVDC）附加直流控制[7-13]提供阻尼，前者通过相位补偿环节提高系统局部阻尼，对于区域间振荡，阻尼提升效果并不明显，后者利用包含振荡信息的功率信号作为控制信号，对区域内和区域间振荡均有不错的效果。多直流系统的出现，使得通过直流附加控制抑制低频振荡的方法更加复杂也更加灵活，附加控制施加于不同的直流系统将获得不同的控制效果，可定义控制敏感点为附加控制器对系统不同振荡模态的最佳安装位置。

本文通过比较振荡模态强相关机组对于各条直流线路灵敏度的大小确定此振荡模态的控制敏感点。首先通过小扰动程序计算得到系统振荡模态及对应于每个振荡模态的强相关机组，在多直流系统的各直流线路参考功率分别施加冲击扰动信号，检测强相关机组功角的变化，加权平均后通过矩阵束辨识得到发电机组功角曲线对于各直流线路的灵敏度，比较灵敏度大小得到振荡模态对应的控制敏感点。

1 矩阵束辨识

矩阵束方法[14，15]是一种参数估计方法，可以从系统响应中提取出振荡模态的频率、相位、幅值等有用信息，近年来，已被运用到电力系统参数辨识中。与Prony算法想法，矩阵束方法在运算效率和抗噪声干扰方面具有明显优势。

设系统响应表示为指数函数的线性组合形式，即

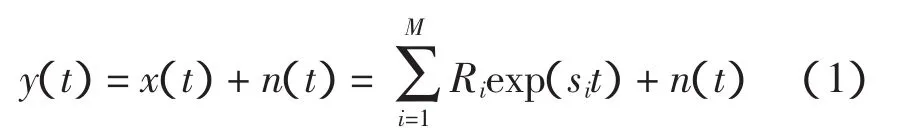
式中：n（t）为噪声；M 为振荡模态数；Ri、αi、ωi分别为第i个振荡模态的幅值、阻尼因子、角频率；si=-αi+jωi。

式（1）的离散形式为

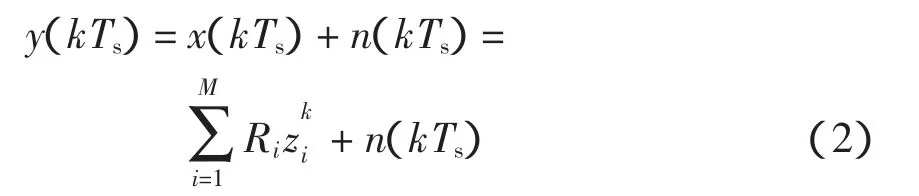
式中：zi为系统极点；Ts为采样周期；k=0，1，…，N-1，N为最大采样数。

先考虑不含噪声的情况，定义两个（N-L）×L矩阵Y1和Y2分别为

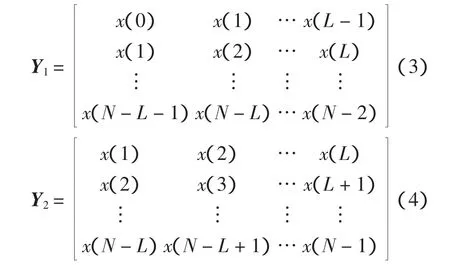
式中，L为矩阵束系数，在含有噪声的矩阵束辨识过程中，L的选取对噪声的过滤有很大影响，通常，L 取值为 N/3～N/4。

将 Y1、Y2分解得到

其中

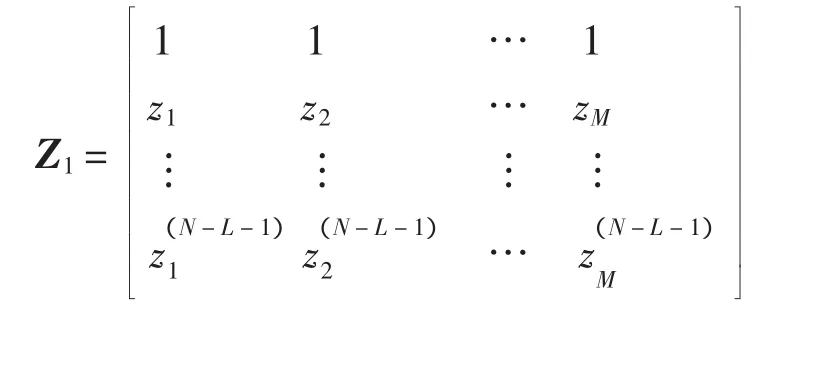
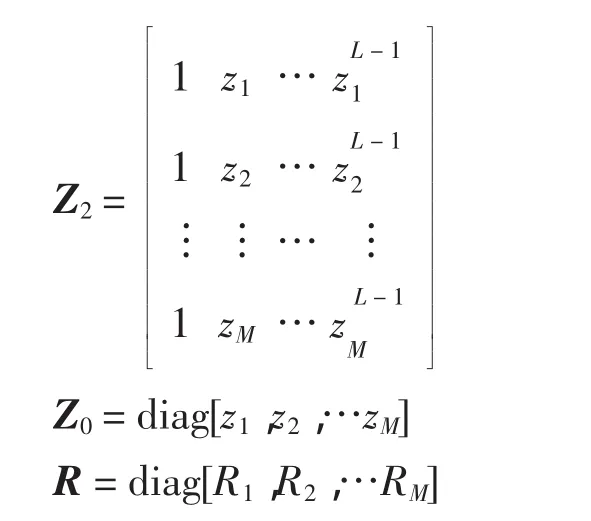
z为系统响应的极点，考虑矩阵束

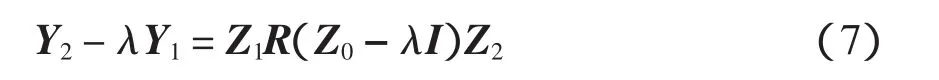
式中：I为M×M阶单位矩阵；若λ≠zi（i=1，2，3…M），矩阵束Y2-λY1的秩为M；若λ=zi（i=1，2，3…M），Z0-λI的第i行元素全部为0，矩阵束的秩降为M-1。因此，信号极点正好是矩阵束的广义特征值，求解极点zi可通过求解矩阵Y1+Y2的特征值得到。

Y1+为 Y1的伪逆矩阵，Y1+= （Y1HY1）-1Y1H，Y1H为Y1的共轭转置矩阵。

设Y1+Y2存在M个非0特征值λi（i=1，2，…，M），则对应模态的阻尼系数及振荡角频率为

通过求解最小二乘问题可求得振荡幅值Ri，其求解式为

对于含有噪声的信号，可按文献[11]的方法由采样序列构造Hankle矩阵，通过奇异值分解求解最大模态数，实现滤波。

2 控制敏感点的求取

基于矩阵束辨识的多馈入HVDC系统低频振荡模态控制敏感点的求取步骤如下。

步骤1通过小扰动程序计算或辨识方法得到系统振荡模态，筛选对系统动态性能影响较大的关键弱阻尼振荡模态M。

步骤2 计算系统中各主要发电机对振荡模态M的参与因子[16]，设各台发电机参与因子为xi。

步骤3 对各台发电机的功角曲线进行加权平均得

式中：δi为第i台发电机功角曲线；n为发电机总数，参与因子较小的发电机可忽略。

步骤4 通过矩阵束辨识方法确定加权平均功角曲线对于多馈入系统各条直流线路的灵敏度，其基本思想是在各条直流功率指令值处分别施加瞬时功率冲击扰动ΔP，检测扰动后各发电机功角变化情况，并通过矩阵束辨识功角曲线δ，取振荡模态M对应频率的幅值R，计算发电机对于直流线路的灵敏度为

可以认为，灵敏度越高的直流线路L，越适合附加直流控制来抑制模态M的振荡，即直流线路L是对于振荡模态M的控制敏感点。

步骤5 若系统中存在多个弱阻尼振荡模态，可重复步骤2～步骤4求出对于各振荡模态的控制敏感点。

3 附加直流控制

通过直流调制对低频振荡进行抑制通常有3种控制方式即大方式调制、小方式调制、双侧频率调制，直流大方式调制、双侧频率调制[17]主要用来提供同步功率，增强交流系统暂态稳定性，抑制故障后交流联络线上大的功率振荡，直流小方式调制主要用来增加系统功率振荡阻尼而不是提供同步功率，通常用于抑制小干扰情况下的功率振荡，小方式调制控制框图如图1所示。

图1 小方式附加控制框图Fig.1 DC small mode complementary controller block diagram

附加控制器参数选择根据文献[18]的理论，采用综合性能指标进行参数整定，参数整定要使目标函数最小，即

式中，X通常为能描述系统动态过程的变量与其对应的稳态值之间的偏差量。选择功角、功率、频率偏差的综合指标作为X，即

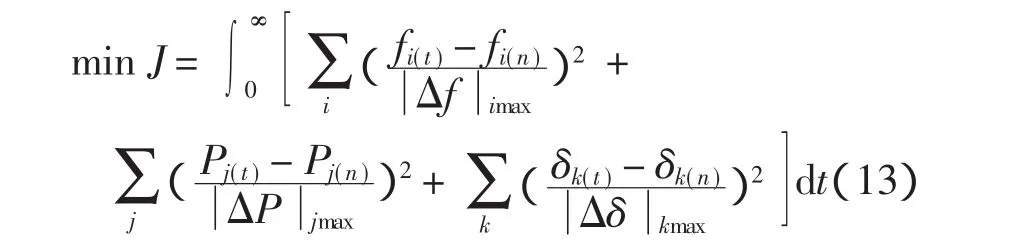
式（13）综合性能指标表示频率偏差、功率偏差、功角偏差归一化平方和最小，从物理意义上来说，综合性能指标越小，说明系统振荡平息越快，也就是系统对振荡具有较强的阻尼和较好的动态性能。

4 算例验证

以2010年川渝电网丰大方式为例进行控制敏感点研究，四川电网通过黄岩-万县和洪沟-板桥线路与重庆电网相连，并且通过德宝、向上两条直流分别与华东及西北电网互联。电网互联如图2所示。

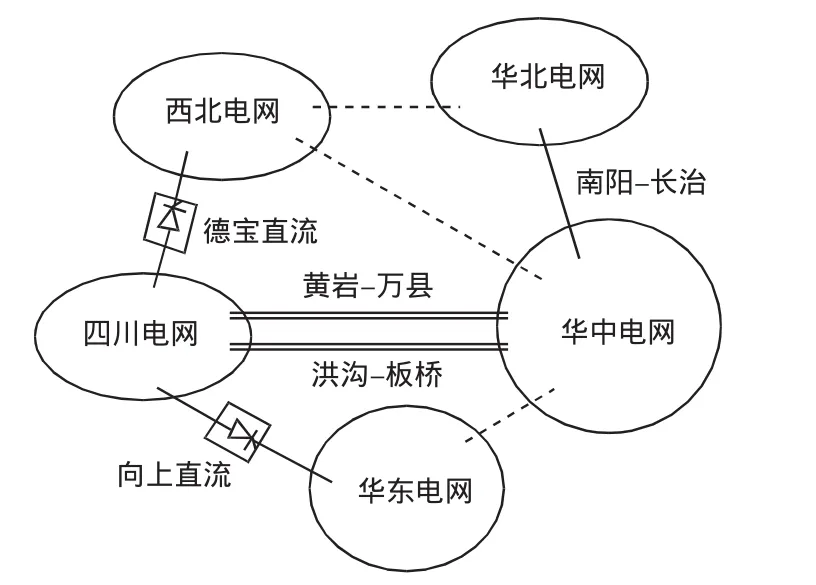
图2 区域互联Fig.2 Electrical area division

通过小扰动计算，可得到四川电网同重庆电网之间的振荡模态为0.4 Hz，计算各发电机对于此振荡模态的参与因子确定强相关机组，对于川渝电网振荡模态参与因子较大的为万和、云弹、宝珠寺等机组。为了不影响系统稳定运行，在无直流调制的情况下，分别在德宝直流和向上直流功率指令值上施加150 MW的功率冲击，对上述强相关机组的功角响应曲线加权平均并进行矩阵束辨识，结果如表1和表2所示。

从表中可以看出，发电机功角曲线在德宝及向上两条直流功率冲击扰动下主振频率均为0.4 Hz左右，此模态对应的振荡幅值德宝直流扰动情况下大于向上直流，强相关机组对于德宝直流功率变化灵敏度更高，对应于0.4 Hz振荡模态的控制敏感点即德宝直流。

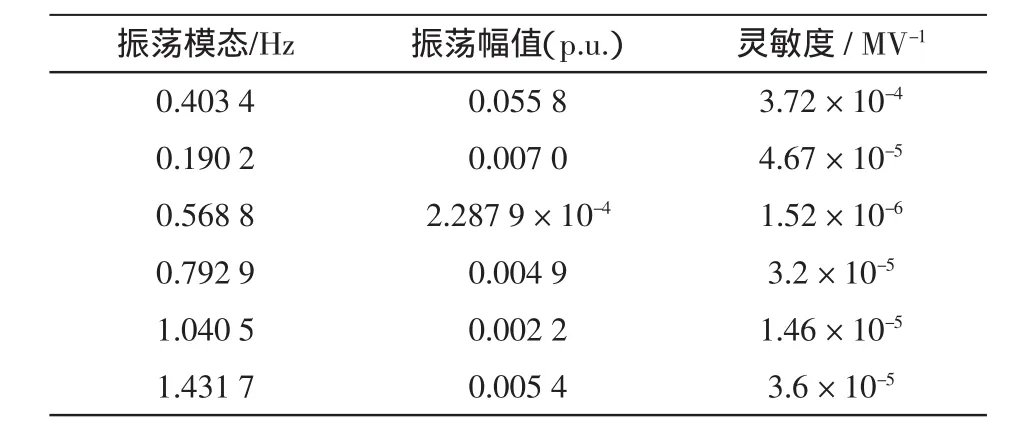
表1 发电机功角曲线的矩阵束辨识结果（德宝直流扰动）Tab.1 Matrix Pencil identification of generator powerangle curve（perturbation on Debao DC system）

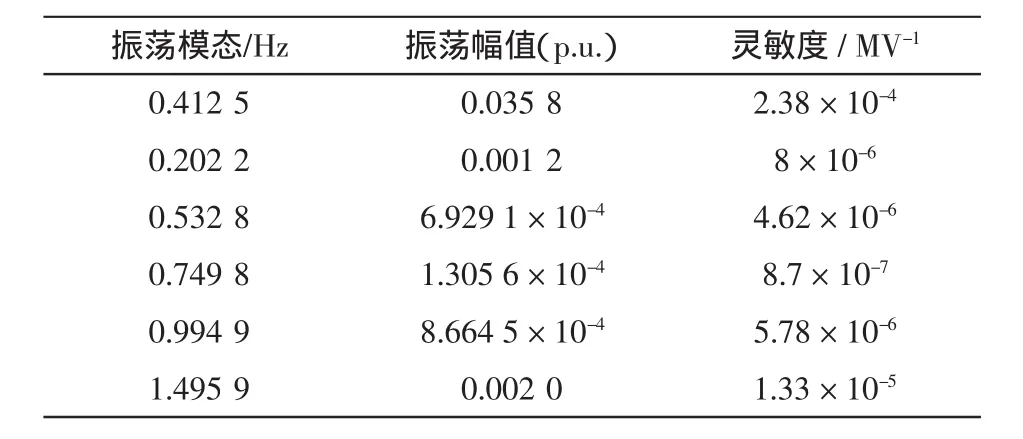
表2 发电机功角曲线的矩阵束辨识结果（向上直流扰动）Tab.2 Matrix Pencil identification of generator powerangle curve（DC upwards disturbances）

为了进一步验证求得的控制敏感点的准确性，使用BPA仿真程序进行时域仿真，0.2 s在洪沟-板桥线路设置三相短路故障，0.3 s切除线路。选择黄岩-万县线路有功功率进行观测分析。分别在无直流调制、德宝直流调制、向上直流调制3种情况下进行仿真，直流附加控制选择小方式控制，主要控制参数K通过综合性能指标进行整定，其余参数取工程经验值。仿真结果如图3所示。

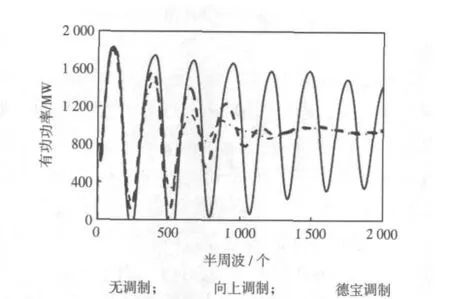
图3 黄岩-万县有功功率曲线Fig.3 Huangyan-Wanxian active power curves

从图中可以清楚看到两种调制方式对于联络线上功率振荡均有较好的效果，但是德宝直流调制下振荡衰减更快，效果更佳。

进一步采用矩阵束方法对功率曲线进行辨识，得到如表3所示结果。从表中看出两种调制方式均能大幅度增加振荡模态的阻尼比，相对而言，德宝直流调制提升阻尼效果更多，因而对振荡模态的抑制效果更佳，这直接证明了控制敏感点的准确性。

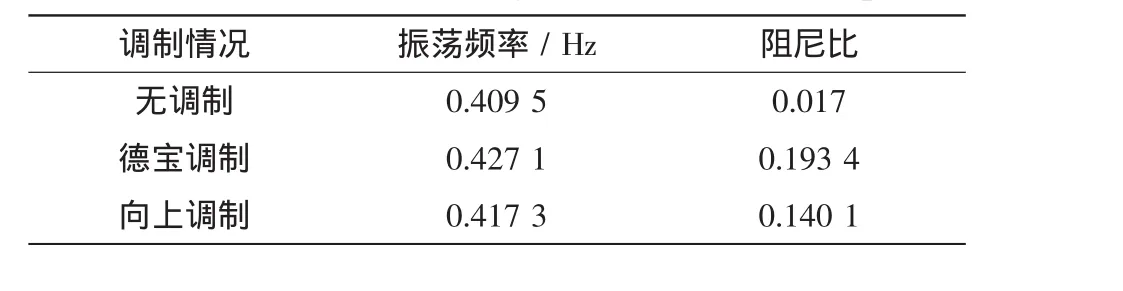
表3 黄岩-万县有功功率辨识Tab.3 Identification of Huangyan-Wanxian active power

5 结语

本文对多馈入HVDC系统结构下通过附加直流控制抑制低频振荡的方法进行了研究，提出了通过矩阵束方法辨识出振荡模态强相关机组同多馈入的各条直流之间灵敏度关系，进而挖掘出振荡模态对应的直流控制敏感点，理论和仿真实验均表明，在控制敏感点附加直流控制会获得相对于其他直流调制更佳的控制效果。

多馈入HVDC系统由于结构复杂，因此研究难度较大，尤其对于不同运行方式，多馈入的各条直流系统的控制相互协调、配合问题，将是未来研究的一个重要方向。

[1]李兴源.高压直流输电系统 [M].北京：科学出版社，2010.

[2]Kundur P.Power System Stability and Control[M].New York：Mc Graw-Hill Inc，1993.

[3]薛禹胜，郝思鹏，刘俊勇（Xue Yusheng，Hao Sipeng，Liu Junyong）.关于低频振荡分析方法的评述（A review of analysis methods for low-frequency oscillations）[J].电力系统自动化（Automation of Electric Power Systems），2009，33（3）：1-8.

[4]Nambu M，Ohsawa Y.Development of an advanced power system stabilizer using a strict linearization approach[J].IEEE Trans on Power Systems，1996，11（2）：813-818.

[5]Wu Chi-Jui，Hsu Yuan-Yih.Design of self-tuning PID power system stabilizer for multimachine power systems[J].IEEE Trans on Power Systems，1988，3（3）：1059-1064.

[6]范国英，郭雷，孙勇，等（Fan Guoying，Guo Lei，Sun Yong，et al）.BFO-PSO 混合算法的 PSS 参数优化设计（Parameters optimize of PSS based on BFO-PSO hybrid algorithm）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（6）：28-31.

[7]孙勇，Karimpour A，牟晓明，等（Sun Yong，Karimpour A，Mou Xiaoming，et al）.采用SVD 方法的附加阻尼控制器配置（Allocation of supplementary damping controller using singular value decomposition method）[J].高电压技术 （High Voltage Engineering），2009，35 （10）：2575-2580.

[8]李兴源，陈凌云，颜泉，等（Li Xingyuan，Chen Lingyun，Yan Quan，et al）.多馈入高压直流输电系统非线性附加控制器的设计（Design of nonlinear complementary controllers for multi-infeed HVDC transmission systems）[J].中国电机工程学报 （Proceedings of the CSEE），2005，25（15）：16-19.

[9]刘红超，李兴源（Liu Hongchao，Li Xingyuan）.基于 prony辨识的交直流并联输电系统直流阻尼控制的研究（Study of DC damping control in AC/DC transmission systems based on Prony method）[J].中国电机工程学报（Proceedings of the CSEE），2002，22（7）：54-57.

[10]陈树恒，李兴源，武陵云，等（Chen Shuheng，Li Xingyuan，Wu Lingyun，et al）.基于降阶模型辨识的交直流混合输电系统广域阻尼控制（Wide-area damp control for AC/DC hybrid transmission systems based on identification of reduced order model）[J].电网技术（Power System Technology），2007，31（17）：36-40，55.

[11]刘红超，李兴源，王路，等（Liu Hongchao，Li Xingyuan，Wang Lu，et al）.多馈入直流输电系统中直流调制的协调优化（Coordination and optimization of HVDC modulations in multi-infeed HVDC transmission system）[J].电网技术（Power System Technology），2004，28（1）：5-9.

[12]徐梅梅，李兴源，王渝红，等（Xu Meimei，Li Xingyuan，Wang Yuhong，et al）.德宝直流调制对四川电网阻尼特性的影响（Impact on the damping charactristics of Sichuan power grid by Debao DC modulation）[J].电力系统保护与控制（Power System Protection and Control），2010，38（23）：141-146.

[13]Pilotto L A S，Szechtman M，Long W F，et al.Synchronizing and damping torque modulation controllers for multiinfeed HVDC systems[J].IEEE Trans on Power Delivery，1995，10（3）：1505-1513.

[14]Sarkar T K，Pereira O.Using the matrix pencil method to estimate the parameters of a sum of complex exponentials[J].IEEE Antennas and Propagation Magazine，1995，37（1）：48-55.

[15]Crow M L，Singh A.The matrix pencil for power system modal extraction [J].IEEE Trans on Power Systems，2005，20（1）：501-502.

[16]彭谦，马晨光，杨雪梅，等（Peng Qian，Ma Chenguang，Yang Xuemei，et al）.线性模态分析中的参与因子与贡献因子（Participation factors and contribution factors in linear modal analysis）[J].电 网 技 术 （Power System Technology），2010，34（2）：92-96.

[17]魏巍，王渝红，李兴源，等（Wei Wei，Wang Yuhong，Li Xingyuan，et al）.交直流电力系统PSS和直流附加控制的协调（Coordination of PSS and DC additional controller for AC/DC power system）[J].电力自动化设备（Electric Power Automation Equipment），2010，30（1）：53-57，61.

[18]吴华坚，王渝红，李兴源，等（Wu Huajian，Wang Yuhong，Li Xingyuan，et al）.基于综合性能指标的交直流混合系统直流调制研究（Study on DC modulation for AC/DC hybrid transmission system based on comprehensive performance index）[J].电力系统保护与控制（Power System Protection and Control），2010，38（22）：68-73.