直驱永磁同步风力发电机的等效建模

肖园园，李欣然，张元胜，马亚辉，徐振华

（湖南大学电气与信息工程学院，长沙 410082）

社会日益发展，人们对电力的需求逐步增大，随着分布式能源的大量使用，不仅改变了传统配电网的负荷拓扑结构，也给电力系统运行分析带来一系列亟待解决的问题，考虑分布式电源影响的配电网综合负荷建模即是其中之一[1-3]。风力发电在分布式新能源发电中发展迅猛，尤其是直驱永磁同步风力发电机（directly driven wind turbine with permanent magnet synchronous generator，DPMSG）因其维护成本低、噪音小、效率高，具有较好的低压穿越能力（lowvoltageridethrough，LVRT）、运行可靠而倍受青睐[4]。本文在研究直驱式风机机理特性及控制方式的基础上，着眼建立能合理描述直驱式风机外特性的机电暂态等效模型。

针对含D-PMSG的配电网综合负荷建模主要有两大问题：首先，基于总体测辨法的负荷建模需要进行大量的运行特性仿真，如何构建符合实际的仿真系统并获取暂态数据是开展建模工作的前提；其次，作为配电网综合负荷的一部分，D-PMSG应作如何等效以满足电网暂态仿真计算对等效模型的要求。

文献[5-6]采用异步电机结合电力电子元件等效异步风机及双馈风机。文献[7-10]针对直驱式仿真模型控制方式及变频器的结构优化上进行了详细分析。文献[11]基于变流器控制策略研究需要建立了D-PMSG机组的详细数字仿真模型。文献[12]采用电阻和直流反电势串联等效电路作为逆变器的直流侧负载模型。尽管D-PMSG的建模研究有不少成果发表，但是从电网机电暂态仿真所需模型要求出发的建模研究则鲜见报道。为完善电力系统机电暂态仿真计算中风力发电系统的暂态模型体系，本文的工作具有理论与实际工程意义。

基于上述目的，本文在研究直驱风机自身机理特性及运行控制方式的基础上，利用SimPowerSystems仿真工具构建了作为分布式电源的直驱风力发电系统；并在此基础上，通过暂态特性分析，从负荷建模研究的角度，提出适合描述其外特性的机电暂态等效模型，通过系列仿真及辨识建模对提出的等效模型进行有效性验证。

1 D-PMSG控制和仿真系统

1.1 D-PMSG系统结构及运行状态分析

D-PMSG是由风轮机直接驱动永磁机，并通过全功率变频器上网。与恒速恒频鼠笼风机与变速恒频双馈风机相比，直驱风机结构更为简单，控制更加灵活，效率更高。

直驱风机基本结构如图1所示，主要由风轮机模块、永磁同步发电机模块、全功率电力电子变频器模块、滤波模块组成。

图1 D-PMSG基本结构Fig.1 Basic structure of D-PMSG

图中 is、ig表示机侧与网侧电流，Lfilter、Cfilter表示滤波部分，R、L为线路阻抗。

全功率变频器模块是直驱控制系统的核心，本文所建仿真系统选用由全控电力电子器件构成的背靠背全功率交直交变频器[9]，通过解耦控制使得有功、无功及转速在一定范围内任意调节，有效实现最大功率追踪（maximum power point tracking，MPPT）。工作时风轮机根据风速及风向调节机械转速和桨距角来实现最大功率跟踪，并带动永磁机变速转动，产生频率变化的三相电压电流，经变频器整流逆变得到与电网频率一致的交流电，滤波后实现直驱式风力发电机安全并网发电。

1.2 D-PMSG变频器控制策略

机侧控制器主要实现最大功率跟踪和对整流器的控制。采用转速外环及电流内环的双环解耦控制策略，外环根据MPPT给出的转速整定值，按照转速与电磁功率、电流的关系，来调整电流内环整定值，并解耦控制输出的功率，进而控制电磁转矩，使转速调整到最大功率点对应的转速[13-14]。

网侧与机侧控制方案基本一致，主要采用电压外环及电流内环控制策略。外环通过锁相环提取系统频率、相角及dq轴电压分量，并利用直流电压控制得到电流控制参考值，内环通过整定无功电流为零，使得系统几乎不吸收也不发送无功，实现单位功率因数输出。

2 暂态过程中D-PMSG的动态特性

2.1 构建含D-PMSG发电的配网仿真网络

如何建立描述直驱式永磁同步风力发电机的等效模型以适合于电网暂态仿真的需求，是研究考虑D-PMSG的配电网综合负荷建模的最终目的。基于实验室以往工作，恒速恒频风机采用异步电机等效的研究已较为成熟，而异步电机是否可以同样应用于直驱风机的等效呢？通过从机理上分析比较可知：异步电机是由定子电流励磁，定子磁场旋转从而在转子感应电流与定子磁场相互作用下产生电磁转矩，转矩与转速（频率）密切相关；而永磁同步机由永磁体励磁，其磁场基本恒定，只需对应的电枢导体内通以电流即可产生转矩，即转矩只取决于电流大小，与转速无关。因此，异步电机模型难以描述直驱永磁同步风机的外特性。

仿真研究表明，由于永磁机不需要外部电源励磁，且在控制方式作用下，在风速不变时，机侧q轴电流与电磁转矩基本恒定，使得输出功率稳定，即可以认为机侧是一个恒功率的电流源。但电力系统建模是为电力系统暂态仿真分析服务的，其准确与否直接关系到系统规划、运行和控制。因此在故障发生的暂态过程中，D-PMSG发电系统是否还能保持这种特性有待深入研究。

2.2 等效描述

2.2.1 动态特性分析

在实际系统中，风电场的风机一般经过35 kV变电箱统一并网到110 kV大电网中，且电力系统实际运行中，以发生三相短路故障最为严重，因此，应用Sim Power Systems工具箱，本文构建如图2所示的仿真系统。通过对三相短路故障下的暂态特性进行分析，验证所提出的等效模型是否可以合理的描述系统暂态。

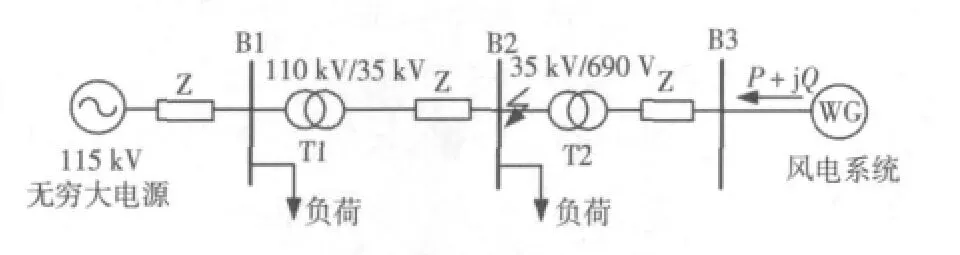
图2 含直驱风电系统单线图Fig.2 Single line figure of distribution system with D-PMSG wind turbine

假设在风速稳定的情况下，在3.0～3.2 s的仿真时间段内，35 kV的B2母线处发生持续时间为0.2 s的三相短路故障，观察接入B3节点的单台额定功率为2 MW的直驱式风力发电机入网点的母线电压、发出的有功功率及无功功率，分析在暂态过程中D-PMSG的动态特性，如图3所示。

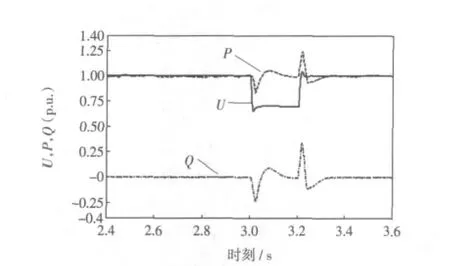
图3 D-PMSG动态特性Fig.3 Dynamic characteristics of D-PMSG

图3中表明，当在35 kV母线上发生一定程度的三相短路故障时，由于故障导致风机并网点电压跌落，变频器无法正常向电网输送电能，故有功输出减小；无功随整定值的限制，基本维持在零，但因故障程度较大，无功在暂态时轻微波动。随着故障切除，电网电压的恢复，逆变器输出的有功及无功逐步恢复至额定值，系统重新进入稳态。直驱式风力机接入电网能在小扰动时基本稳定输出，且当外部发生严重的三相短路故障时系统电压很低的情况下仍不切机，故可见直驱式风力发电机低压穿越性能较好。

2.2.2 等效电路

综上所述，为研究系统故障时的D-PMSG的暂态特性，必须构建有效的数学模型来准确描述其动态行为。在深入研究风机动态特性的基础上，通过仿真结果观察，可知在系统35 kV线路上发生三相短路后，由于全功率变频器的隔离作用，来自电网的系统故障对电机侧的影响很小，且由于风机的转动惯性大，机侧转子速度稳定，机侧变频器输出功率基本恒定，因此结合网侧变频器的机理特性及系统结构，可将D-PMSG等效为用恒定功率控制的电流源、电容、电感及电阻串联表示的系统等值电路来描述其外特性。其电网同步坐标下的等值电路如图4所示，图中各量和下文的模型推导均采用标幺值。

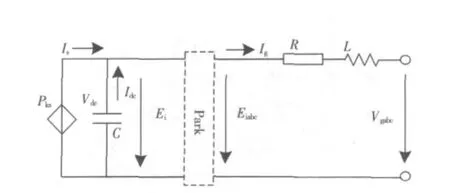
图4 D-PMSG等值电路Fig.4 Equivalent circuit of D-PMSG

图中，Vgabc为风机并网点电压，Ig为逆变器输出电流（即风机注入电网的电流），Eiabc为网侧逆变器电压，R、L为逆变器出口侧至并网点之间等值电阻和等值电感（包括滤波器部分等），忽略滤波电容及网侧逆变器损耗，且只对基波正序电压电流量进行分析，经过派克变换，将电压及电流转换为dq坐标系下后，C为等效变流器直流侧电容，Pks为等效机侧变流器输出功率。由上述分析可知机侧的恒定功率输出特性，故认为Pks是常数，由稳态运行条件决定。

2.2.3 等效数学模型

根据图4中所构造的D-PMSG的等值电路图及风机系统网侧控制模块方程，以回路电流及并网点电压的三相瞬时值分别作为原始状态相量x和输入激励相量 u，即令 x=[iga，igb，igc]T，u=[Vga，Vgb，Vgc]T；模型参数向量 θ =[R，L，C]T；输出（响应）向量y=[P，Q]T，则D-PMSG的等值模型写成状态方程的一般形式[15]为

式（1）包括系统动态微分方程和输出方程，由等值电路可知，动态微分方程具体形式为

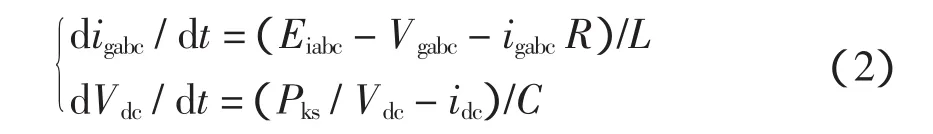
上式是三相瞬时值所对应的微分方程，式中变量与图4中变量对应。在实际研究中为方便仅考虑dq坐标系下的动态方程，因此将上式所对应的变量进行派克变换，即可得dq坐标系下动态微分方程为

式中：Ei，d=mdVdc；Ei，q=mqVdc；ω 为系统标幺频率；R、L、C 是独立辨识参数；md、mq为辨识过程中的中间变量，是经过逆变器调制时对应dq坐标的调制比。在给定模型激励并确定初始条件后，求解上式即可解得 Ig，d、Ig，q再经派克逆变换，即可求出同步坐标系的电流Ix、Iy，进而可得D-PMSG系统的上网功率，即模型响应为

焦页42号平台是涪陵工区首次“井工厂”同步压裂施工，也是张相权参与的该工区规模最大、设备使用最多、施工工序最复杂的一次超大型施工作业。作为队长，张相权丝毫不敢马虎。那段时间，每天的施工运行都达到饱和状态，每个工具都得详细检查才入井，每个工序都得亲自确认才放心，最轻松的一天睡6小时，最晚的只有不到4小时。

上述几组公式即构成了D-PMSG发电系统三阶等效模型的完整形式。

2.2.4 模型初始稳态

模型的初始稳态即是其必须满足的边界条件，据此才可确定动态微分方程的状态变量初始值及初始稳态功率。

已知稳态时的激励 V0（[Vlx，0，Vly，0]T） 与响应[P0，Q0]T，从而可求出电流响应i0（[ix，0，iy，0]T）及Ei0如式5所示。

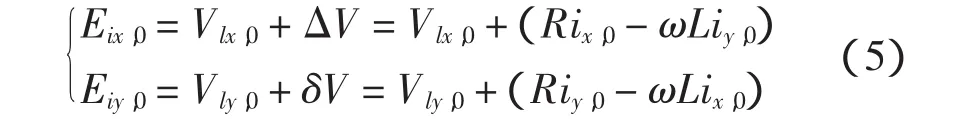
通过xy坐标系与dq坐标系之间的转换，即可得[id，0，iq，0]T，及逆变器出口侧电压[Eid，0，Eiq，0]T。忽略逆变器功率损耗，通过求解逆变器出口侧功率，可得机侧输入功率及电容电压，其计算过程为

至此，式（3）中的微分方程组所需初始条件均已确定。在后续的辨识过程中机侧输入功率保持不变，将风机、永磁机及整流器等效成一个输出功率恒定的电流源。为使描述效果更佳，可对md、mq、Idref调整修正。

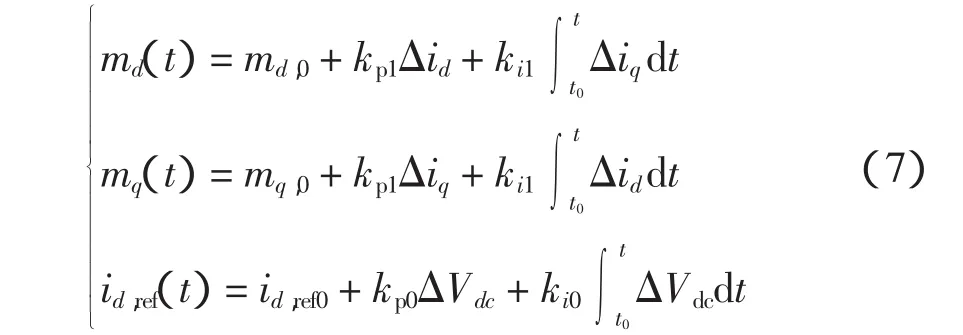
其中：

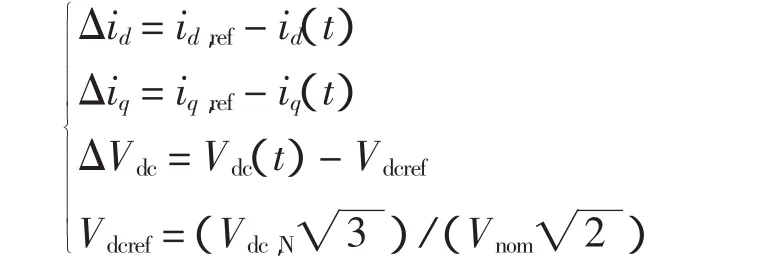
式中：Vdc，N为直流电压稳态值，Vdc，N=1 200 V；Vnom为并网点系统额定电压 Vnom=690 V，id，ref0=id，0，iq，ref=0；kp0、ki0、kp1、ki1分别对应网侧双环控制相应的PI参数。

3 模型检验

3.1 描述能力

对不同程度故障下的数据样本进行辨识，结果如表1所示。表中参数电压实际基准值为690 V，功率基准值为2 MW。由于等效模型为根据RLC三者合成电路后的特性来描述风机的外特性，故等效元件仅是类似于实际系统中的相应元件所在位置，故等效参数值与实际值略有差别是合理的。

限于篇幅，给出当短路电阻为8 Ω（ΔV=45%）时的实测响应及相应的模型响应曲线，如图5所示。从参数稳定性角度分析，模型对同一仿真系统的不同实测样本辨识所得参数的分散度在一定程度上能有效检验模型的参数稳定性，即模型可辨识性。从表1列出的8组辨识参数分析，尽管它们对应的故障程度相差较大，但同类参数的分散性较小，从而证明模型具有较好的参数稳定性。残差为实测数据与模型相应数据之间的差值的体现，残差较小从而说明模型拟合效果良好。

表1 模型参数辨识结果Tab.1 Results of load model parameters identification

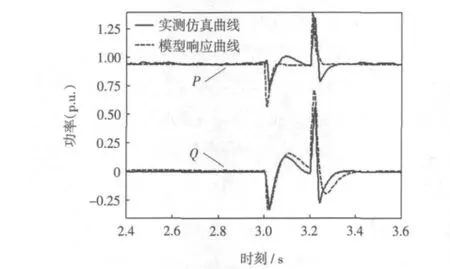
图5 等效描述模型拟合效果Fig.5 Model fitting results of equivalent description

综上所述，采用本文所提出的三阶微分方程描述的等效模型能够较好的描述D-PMSG发电系统的特性。

3.2 泛化能力

模型泛化能力是检验该模型及参数是否适应其他情况下的暂态稳定性描述的一个典型指标，将其他程度的三相短路故障时的电压激励依次施加于短路电阻为8 Ω（ΔV=45%）时辨识所得的模型，比较相应的模型与仿真实测响应的拟合程度。由于篇幅限制，仅给出两种故障程度下对应的内插外推响应曲线图，残差如表2所示。图7为在一定故障（三相短路，电压跌落45%）下，仿真系统电压、电流的基波正序分量有效值与等效模型端口电压、电流的拟合效果。

检验结果表明，虽然拟合样本与建模样本的故障程度不一样，但模型具有良好的内插和外推特性，泛化能力较好。

3.3 模型物理意义及其适应性讨论

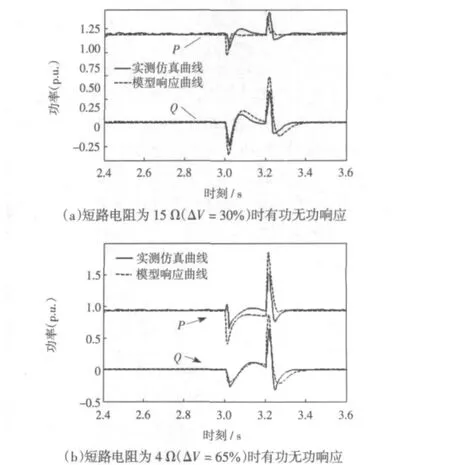
图6 内插外推能力验证Fig.6 Curves of interpolation and extrapolation tests

图7 电压、电流基波正序量的拟合效果Fig.7 Fitting effect of fundamental positive-sequence of voltage and current

（1）模型的物理意义。由于全功率变频的隔离作用及永磁机本身特性，使得电网故障对风机电机侧影响较小，机侧变频器以恒定功率输出，因此永磁风机可以视为恒功率电流源；在系统故障时，忽略滤波器对地电容及暂态变化，可将直驱风电系统等效为RLC电路，此即本文所提出的动态等效模型的物理背景。尽管变流器的网侧逆变控制可使风电系统几乎单位功率因数输出，但故障程度较大时，随暂态电流变化，滤波电感在故障时向外释放磁场能量，系统频率及无功会轻微波动。

（2）派克变换的必要性，文中构建动态微分方程时，对同步坐标下的动态方程式（3）经派克变换得到dq坐标下的表达形式，进而可将解耦后的交流量按照直流量来控制，使模型具有描述对称和非对称故障扰动下暂态过程的普遍适应性。

（3）暂态过程中（特别是激励跃变时刻）的仿真测量值与辨识模型响应稍有差别，是由于仿真中考虑有电力电子元件的存在，必然会有短时的电磁暂态过程，而这是等效模型中忽略的部分，故障越大时，变频器与滤波器的电磁暂态越明显，则会产生小段时间内的误差。

表2 内插、外推响应残差Tab.2 Error chart of generalization test

4 结语

本文在阐述直驱永磁同步电机机理特性基础上，采用全功率变频器及双环控制策略，在SimPowerSystems中搭建D-PMSG的发电系统；通过不同程度的扰动仿真分析，证明了所搭仿真模型的稳定性较好。

通过对D-PMSG动态特性研究分析，提出三阶微分方程描述的等效数学模型，并取不同程度故障下的仿真实测数据验证了其合理性，这对于含分布式电源的综合负荷建模工作很有意义。

为进一步扩展本文所研究内容的广泛适用性，考虑含配电网络的直驱式风电系统综合负荷等效建模将是下一步研究工作的重点。

[1]余贻鑫，栾文鹏（Yu Yixin，Luan Wenpeng）.智能电网述评（Smart grid and its implementations）[J].中国电机工程学报（Proceedings of the CSEE），2009，29（34）：1-8.

[2]彭彬，刘宁，吴迪（Peng Bin，Liu Ning，Wu Di）.配电网潮流计算中的分布式电源建模（Modeling of distributed generation for distribution system power flow calculation）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2011，23（2）：152-156.

[3]赵宏伟，吴涛涛（Zhao Hongwei，Wu Taotao）.基于分布式电源的微网技术（Review of distributed generation based microgrid technology）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（1）：121-128.

[4]张兴，张龙云，杨淑英，等（Zhang Xing，Zhang Longyun，Yang Shuying，et al）.风力发电低电压穿越技术综述（Low voltage ride-through technologies in wind turbine generation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20（2）：1-8.

[5]李辉，韩力，赵斌，等（Li Hui，Han Li，Zhao Bin，et al）.风电机组等效模型对机组暂态稳定分析结果的影响（Effect of equivalent models of wind turbines on analysis results of transient stability for wind generator systems）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（17）：105-111.

[6]熊飞，王雪帆，张经纬，等（Xiong Fei，Wang Xuefan，Zhang Jingwei，et al）.绕线转子无刷双馈电机的链型等效电路模型（Chain equivalent circuit model of woundrotor brushless doubly-fed machine）[J].电工技术学报（Transactions of China Electrotechnical Society），2010，25（2）：15-21.

[7]姚骏，廖勇，庄凯（Yao Jun，Liao Yong，Zhuang Kai）.永磁直驱风电机组的双PWM变换器协调控制策略（Coordinated control strategy of back-to-back PWM converter for permanent magnet direct-driven wind turbine）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（20）：88-92，107.

[8]张强，张崇巍，张兴，等（Zhang Qiang，Zhang Chongwei，Zhang Xing，et al）.风力发电用大功率并网逆变器研究（Study on grid-connected inverter used in high-power wind generation system）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（16）：54-59.

[9]付勋波，郭金东（Fu Xunbo，Guo Jindong）.直驱式风力发电系统的仿真建模与运行特性研究（Characteristics and simulation model of direct-drive wind power system）[J].电力自动化设备（Electric Power Automation Equipment），2009，29（2）：1-5.

[10]李燕，梁英（Li Yan，Liang Ying）.永磁直驱风电系统电压源型变流技术（Voltage source converter technology in permanent-magnet directly driven wind power system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（1）：65-70.

[11]尹明，李庚银，张建成，等（Yin Ming，Li Gengyin，Zhang Jiancheng，et al）.直驱式永磁同步风力发电机组建模及其控制策略（Modeling and control strategies of directly driven wind turbine with permanent magnet synchronous generator）[J].中国电机工程学报 （Proceedings of the CSEE），2007，31（15）：61-65.

[12]张加胜，张磊（Zhang Jiasheng，Zhang Lei）.PWM 逆变器的直流侧等效模型研究（Research on the DC-side equivalent model of PWM inverters）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（4）：103-107.

[13]赵仁德，王永军，张加胜（Zhao Rende，Wang Yongjun，Zhang Jiasheng）.直驱式永磁同步风力发电系统最大功率追踪控制（Maximum power point tracking control of the wind energy generation system with direct-driven permanent magnet synchronous generators）[J].中国电机工程学报（Proceedings of the CSEE），2009，29（27）：106-111.

[14]姚骏，廖勇（Yao Jun，Liao Yong）.直驱永磁同步风力发电机的最佳风能跟踪控制（Optimal wind-energy tracking control of direct-driven permanent magnet synchronous generatorsforwindturbines）[J].电网技术（Power System Technology），2008，32（10）：11-15，27.

[15]李欣然，钱军，王立德，等（Li Xinran，Qian Jun，Wang Lide，et al）.配电网集结等效的异步电动机综合负荷模型及其总体测辨建模（Synthesis induction motor model of power composite load considering distribution network structure）[J].电工技术学报（Transactions of China Electrotechnical Society），2009，24（4）：175-185.

[16]李培强，李欣然，林舜江（Li Peiqiang，Li Xinran，Lin Shunjiang）.电力负荷建模研究述评（Critical review on synthesis load modeling） [J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2008，20 （5）：56-64，123.