计及风机无功约束的电压稳定性分析

刘 铖，蔡国伟，杨德友，孙 琦

（1.东北电力大学电气工程学院，吉林 132012；2.华北电力大学电气与电子工程学院，北京 102206）

近年来，风力发电发展迅速。风能作为一种绿色的可再生能源已成为世界能源的重要组成部分。随着我国能源政策的调整，风电展现了广阔的发展前景。

风能具有随机性、间歇性等特点，随着风电机组容量和风电场规模增大，迫切需要研究大型风电场并网后对电力系统稳定的影响[1-2]。风电的接入将会给系统电压稳定带来影响，如何合理评估含风电场系统的电压稳定问题是极其有意义的。

目前，针对风电场接入系统的电压问题已进行了大量的论述。文献[3]提出基于PV曲线的风电场接入系统稳态分析方法及两个风电场同时接入系统的分析方法，分析了风电场接入系统的电压要求及风电场运行对区域电网网损影响。文献[4，5]基于连续潮流法对异步机风电场与基于双馈感应电机（doubly-fed induction generator，DFIG）的变速风电场接入电网后系统的静态电压稳定裕度进行比较了研究。

但是，这些文献重在比对不同风机类型对系统电压稳定的影响，均没有涉及考虑双馈感应风机风电场无功限制对系统电压稳定的影响，且未深入分析失稳原因。

本文对基于双馈感应风力发电机组风电场进行研究，建立双馈风机的数学模型，通过绘制风电场接入点PV曲线，分析采用不同无功限制下双馈风力发电机组风电场接入系统后的静态电压稳定性，同时通过分岔理论分析失稳类型和对风机接入系统裕度的影响。结果表明，DFIG考虑功率极限对电压稳定裕度有一定的影响且影响分岔类型，考虑DFIG发生的不同分岔可以更真实地揭示系统失稳原因和提供实际裕度。

1 风力发电机组的稳态数学模型

双馈异步风力发电机等值电路如图1所示[6]。

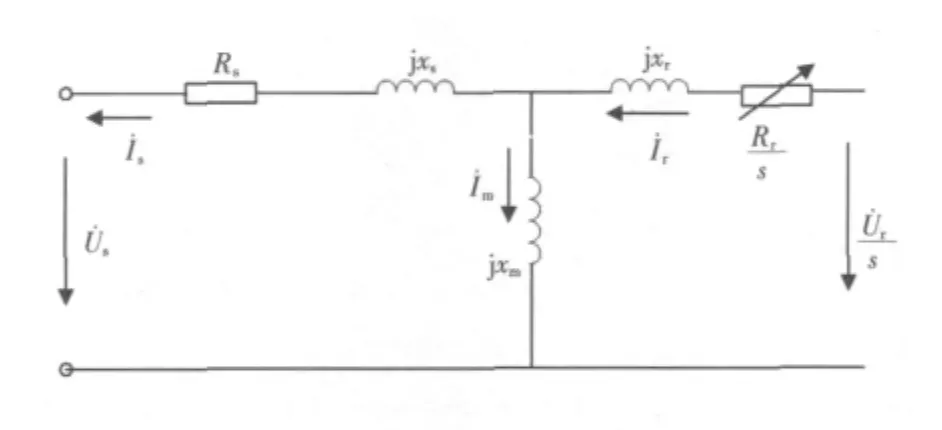
图1 双馈异步风力发电等值电路示意Fig.1 Equivalence circuit of a DFIG wind

注入系统总有功Pe由两部分组成，一是定子绕组的有功Ps，另一部分是转子绕组发出或消耗的有功Pr。

由于变流器吸收或发出的无功很小，可近似认为风电机组无功功率Qe等于定子绕组无功功率Qs，所以风电机组注入系统有、无功功率为

风电机组注入系统转子绕组的有功功率[7]为

定子侧有、无功运行范围主要受变流器转子侧电流限制，可表示为

式中，Irmax是变流器电流限制值。

将式（1）分别代入式（2）和式（3），可得

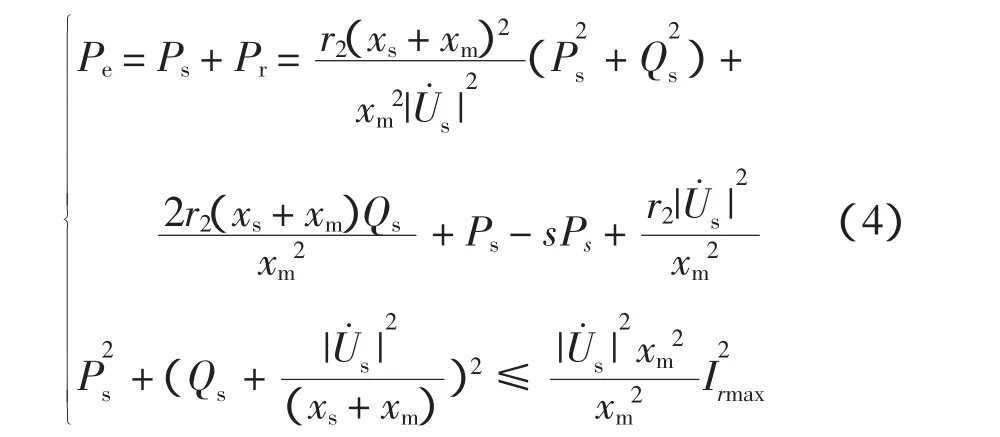
相应的无功功率极限可由式（4）求得。

2 含风电系统的分岔点类型分析

包含上述风电系统的电力系统稳态数学模型可写成

式中：x为状态变量；y为代数量，包括电压幅值和相角；λ为负荷参数。

电力系统分岔分析方法可分为静态分岔分析和动态分岔分析两种。下面介绍两种在静态分岔分析中经常遇到的分岔：鞍结分岔（saddle induced bifurcation，SNB）和极限诱导分岔（limit induced bifurcation，LIB）。并将二者用于含风电的分析中。

2.1 鞍结点分岔

鞍结分岔[8]的条件为

或

式中，v和w分别为右、左特征向量。

图2所示的是通常的PV曲线，在点SNB发生鞍结分岔。

2.2 极限诱导分岔

极限诱导分岔[2，8-10]点可定义系统的解为

图2 鞍结分岔Fig.2 Saddle node bifurcation

式中，ρ（y）是附加限制条件，对于平衡节点和发电机PV节点条件为

或对负荷节点应满足条件为

极限诱导分岔是发电机到达无功极限引起的，图3给出了发电机的PV曲线图。Vs为给定值，Q=Qlim为发电机处于无功极限状态下的PV曲线。随着负荷增加，电压水平会降低。如图3的A点，发电机到达无功极限，对于1，点A位于曲线下半部，诱发系统突然电压崩溃。当系统运行在另一情况：如虚线2所示。运行点位于曲线上半部，即不会发生极限诱导分岔。

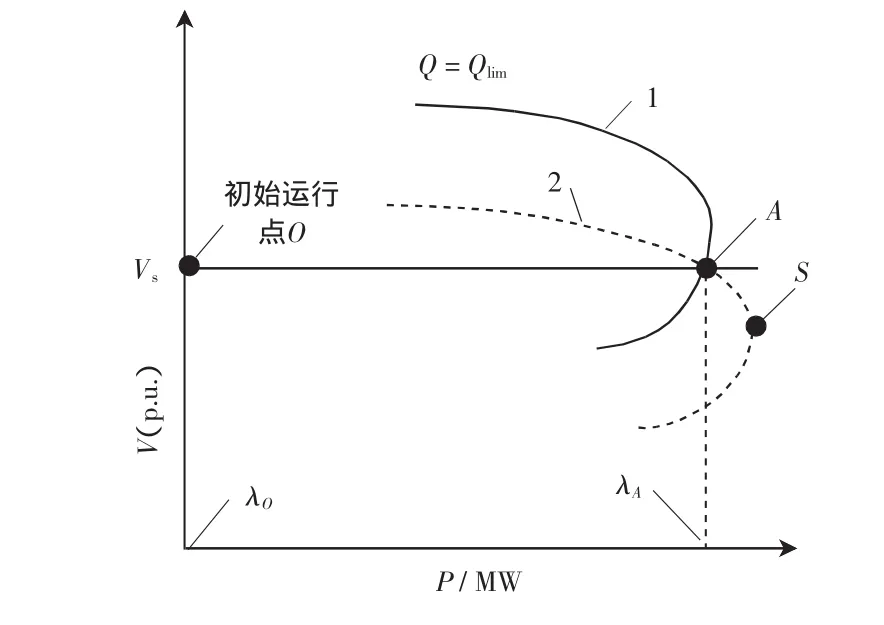
图3 极限诱导分岔Fig.3 Limit induced bifurcation

本文在计及双馈风机无功极限影响下，对双馈风机风场的分岔类型作判别。由于DFIG具有一定的无功支撑作用，能够基本维持风场并网点电压恒定不变，可近似把风力发电机节点等同于同步发电机节点考虑，利用文献[8]对LIB的定义判别风场分岔类型。

3 风电场系统的静态电压稳定分析

在风电系统静态电压稳定性分析中，目前使用比较广泛的是PV曲线法[3]。它通过建立节点电压和一个区域负荷的关系曲线，指示区域负荷水平导致整个系统临近电压崩溃的程度[3-5]。

连续潮流是电压稳定性分析的有力工具，可以克服潮流方程在接近稳定极限运行状态时的收敛问题。连续潮流法从初始稳定工作点开始，随着负荷缓慢变化，沿相应PV曲线对下一工作点进行预估-校正，直到勾画出完整的PV曲线连续潮流计算方法。

应用PV曲线方法分析风电场的静态电压稳定性时，考虑风电注入系统的功率对电压稳定性的影响，则P代表的是风电场的有功功率，V取风电场接入点电压，V也可以是其他节点或机端等关键节点电压。通过连续潮流获得风电场关键节点的PV曲线，进而分析风电场的静态电压稳定问题。

4 算例分析

4.1 风电场及系统简介

采用IEEE30节点标准测试系统作为算例系统[10]，风电场通过升压变压器和135 kV线路接入系统（见图4）。

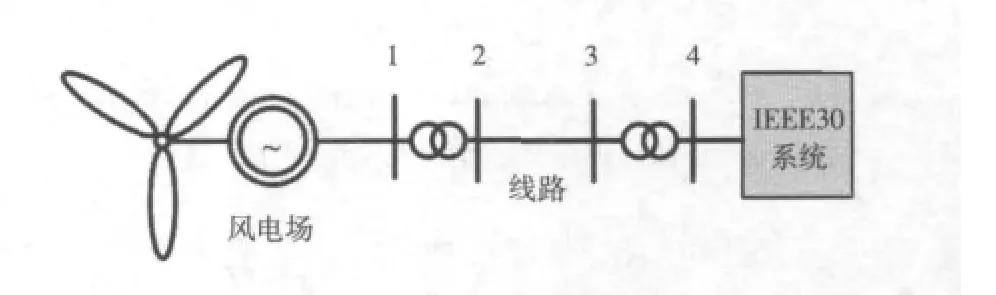
图4 风电场接入的IEEE30节点系统结构Fig.4 IEEE30 node system structure containing wind farm

选择节点4为系统接入点。双馈感应风力发电机组风电场单机容量1.5 MW，参数见文献[11]。系统及风电场均采用标么值，基准容量100 MVA，基准电压为额定电压。风电场地区空气密度为1.224 5 kg/m3，风力机的扫掠面积为1 840 m2。

4.2 考虑DFIG风机无功功率极限限制的风机PV曲线分析

当V=0.9 p.u.时，某1.5 MW DFIG风机无功出力限制曲线如图5所示。

根据上面计算出的DFIG风机无功出力上下限，考虑在DFIG风机功率因数设定不同时，绘制并网点电压随风电场有功出力增加的PV曲线，如图6所示。

图5 某1.5 MW DFIG风机可用无功出力输出范围Fig.5 Schematic diagram of available reactive power output of some kind DFIG with rating of 1.5 MW

图6 1.5 MW DFIG风机风场不同无功出力下的风机PV曲线Fig.6 PV curvs of availables reactive power output of some kind DFIG with rating of 1.5 MW

由图6可知，无功输出越大，风机接入裕度越大，但是同时也会造成风电场接入点电压升高，当无功输出为Qmin时，节点电压随风机注入功率增加而降低，造成电压越限，相比在无功出力为0时，即功率因数为1，电压波动较小，且相对平稳。可见风机应采用功率因数为1的运行方式，与实际中通常的运行方式较为吻合。

当风电场运行在Qmin、Qmax时，风电场并网节点电压PV曲线分别如图7所示。

由图7可见，对于DFIG运行在Qmin情况，随着风电场注入功率的增加，引起了并网点电压下降。相反，对于Qmax的情况，风电场功率增加引起了电网并网点电压的升高。说明DFIG风电场的无功对系统并网节点的电压有着重要的影响，因此DFIG的无功出力运行方式不可忽略。

图7 无功极限情况时风电场的PV曲线Fig.7 PV curvs of wind farm when Qmaxand Qmin

在考虑DFIG风机无功极限的情况下，其风电场的裕度值，如表1所示。

表1 考虑DFIG无功限制下风电机组接入系统的裕度情况Tab.1 Margin conditions of wind generator access to system considering the available reative power output of DFIGMW

由表1可知，DFIG无功出力不同对风电机组接入系统的稳定裕度的影响不同。当运行在无功出力下限时，风电机组接入系统的稳定裕度较小，当运行在无功出力上限时，风电机组接入系统的稳定裕度较大。这是因为DFIG机组具有无功控制能力，其提供的无功能够支撑系统并网点电压，有利于改善系统的静态电压稳定性，增大裕度。

4.3 基于分岔理论的考虑DFIG风机无功功率极限限制的风机PV曲线分析

下面讨论基于分岔理论，考虑DFIG风机无功极限的风电场裕度值，分别进行仿真分析。仿真系统参数同上。取风电场母线的最低限制电压[12]Vs=0.9（p.u.），风电场运行在 Qmin、Qmax情况时，对风场并网点母线电压PV曲线进行分岔分析，如图8所示。

图8 无功极限情况时风场的PV曲线Fig.8 PV curves of wind farm when Qmaxand Qmin

由图8可见，对于Qmin的情况，风机发生了鞍结点分岔导致了系统电压失稳。对Qmax的情况，2者没有交点，这是由于仿真软件和算法未呈现出曲线的下半段，但实际DFIG风机的最大无功限制曲线应和Vs相交于曲线下半段，根据图3原理分析可知是由于风机发生极限诱导分岔导致了电压失稳。

考虑无功极限分岔时，不同无功出力时风机的裕度值不同。对Qmin的情况，风机接入系统的稳定裕度并未改变，仍为168.0 MW，但是对于Qmax情况，由于发生LIB分岔其裕度值应小于正常的605.2 MW。

考虑风电场母线的最低限制电压不同时的情况，当为 Vs=0.95（p.u.）时，对 Qmin、Qmax情况，进行分岔分析，如图9所示。

图9所示，由3.1所示的鞍结分岔定义可知，对于Qmin和Qmax的情况，风机均发生鞍结点分岔导致了系统电压稳定性失稳。

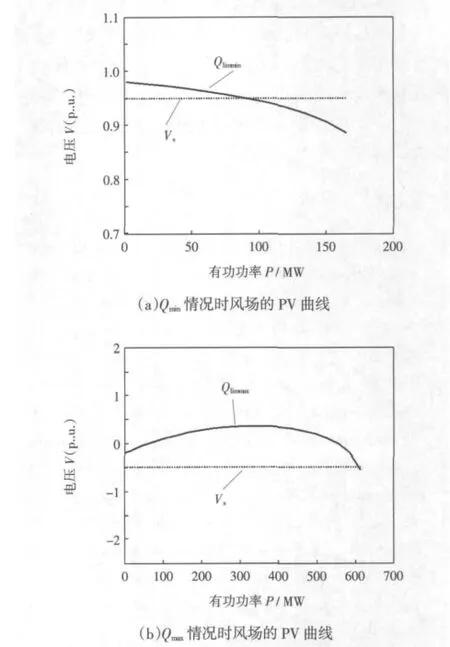
图9 无功极限情况时风场的PV曲线Fig.9 PV curvs of wind farm when Qmaxand Qmin

由仿真结果可知，在Vs=0.95（p.u.）时裕度值与表1相同。DFIG的无功极限下系统的分岔类型不同，即造成风电失稳的起因不同，对风电接入系统的裕度影响不同。考虑DFIG发生的不同分岔可以更真实揭示系统的失稳原因和提供实际裕度。

5 结论

（1）DFIG无功出力不同对风电机组接入系统的稳定裕度的影响不同。对于DFIG运行在Qmin时，随着风电场注入功率的增加，引起了并网点电压下降。反之，对于Qmax情况，风电场功率增加引起了并网点电压的升高。说明DFIG风电场的无功对系统并网节点的电压有着重要的影响，DFIG的无功出力运行方式不可忽略。

（2）当运行在无功出力下限时，风电机组接入系统的稳定裕度较小，当运行在无功出力上限时，风电机组接入系统的稳定裕度较大。这是因为DFIG机组具有无功控制能力，其提供的无功能够支撑系统并网点电压，有利于改善系统的静态电压稳定性，增大裕度。

（3）DFIG考虑功率极限对电压稳定裕度有一定的影响且影响分岔类型。DFIG的无功极限下系统的分岔类型不同，即造成风电失稳的起因不同，对风电接入系统的裕度影响不同。考虑DFIG发生的不同分岔可以更真实揭示系统的失稳原因和提供实际裕度。

[1]马幼捷，杨海珊，周雪松，等（Ma Youjie，Yang Haishan，Zhou Xuesong，et al）.风电系统的电压稳定性分析（Voltage stability analysis of wind power system）[J].电 力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（3）：22-26.

[2]马幼捷，张继东，周雪松，等（Ma Youjie，Zhang Jidong，Zhou Xuesong，et al）.含风电电力系统电压稳定问题的分岔（Bifurcation of steady state voltage stability with wind power system）[J].电 力 系 统 及 其 自 动 化 学 报（Proceedings of the CSU-EPSA），2008，20（5）：117-123.

[3]张义斌，王伟胜，戴慧珠（Zhang Yibin，Wang Weisheng，Dai Huizhu）.基于P-V曲线的风电场接入系统稳态分析（P-V curve based static analysis for integration of wind farm into power system）[J].电网技术 （Power System Technology），2004，28（23）：61-65.

[4]李作红（Li Zuohong）.风电场接入系统静态电压稳定研究（Static voltage stability issues for grid integration with large-scaled wind farms）[J].电网与清洁能源（Power System and Clean Energy），2010，26（10）：53-61.

[5]张瑞明，张新燕（Zhang Ruiming，Zhang Xinyan）.基于普通异步发电机和双馈风力发电机静态数学模型的系统静态电压稳定性研究（Study on static voltage stability of power system based on static models of common and doubly fed asynchronous generators）[J].电网技术（Power System Technology），2011，35（1）：175-179.

[6]Lei Yazhou，Mullane Alan，Lightbody Gordon，et al.Modeling of the wind turbine with a doubly fed induction generator for grid integration studies[J].IEEE Trans on Energy Conversion，2006，21（1）：257-264.

[7]严干贵，王茂春，穆钢，等（Yan Gangui，Wang Maochun，Mu Gang，et al）.双馈异步风力发电机组联网运行建模及其无功静态调节能力研究（Modeling of grid-connected doubly-fed induction generator for reactive power static regulation capacity study）[J].电工技术学报（Transactions of China Electrotechnical Society），2008，23（7）：98-104.

[8]李华强，刘亚梅，Yorino N （Li Huaqiang，Liu Yamei，Yorino N）.鞍结分岔与极限诱导分岔的电压稳定性评估（Voltage stability assessment for saddle node bifurcation and limit induced bifurcation）[J].中国电机工程学报（Proceedings of the CSEE），2005，25（24）：56-60.

[9]Milano F.PSAT，Matlab-based power syttem analysis toolbox[EB/OL].http：//www.uclm.es/area/gsee/Web/Federico，2007.

[10]Alsac O，Stott B.Optimal load flow with steady-state security[J].IEEE Trans on Power Apparatus and Systems，1974，93（3）：745-751.

[11]申洪（Shen Hong）.变速恒频风电机组并网运行模型研究及其应用（Studies on Integrated Variable-Speed Constant-Frequency Wind Turbine Models and the Application） [D].北京：中国电力科学研究院（Beijing：China Electric Power Research Institute），2003.

[12]许珊珊，汤放奇，周任军，等（Xu Shanshan，Tang Fangqi，Zhou Renjun，et al）.不同风电系统动态电压稳定的分岔分析（Bifurcation analysis on dynamic voltage stability of power grid connected with different wind power systems）[J].电网技术（Power System Technology），2010，34（5）：67-71.