电机同步传动自适应模糊PID控制算法研究
2013-07-02郭昌
郭 昌
(安徽大学电气工程与自动化学院,合肥 230601)
前言
同步运动控制这类问题广泛应用于高精度、多变量控制系统中,其控制性能的好坏直接影响到整个控制系统的稳定性和可靠性。因此,研究、设计和开发双电机以及多电机的同步运动控制系统具有重大的现实意义和工程实际应用价值。
在实际的控制系统中,由于系统的状态和参数等在发生变化时,会导致系统出现状态和参数的不确定性,传统的 PID 控制不能智能化地自适应系统参数的变化,往往会导致控制系统性能不能满足实际要求。由于模糊控制理论不需要对象具有精确的数学模型,可以用模糊数学的理论知识来模仿人类大脑的思维方式,对模糊现象进行判定和识别,从而给出准确的控制参数,对被控对象进行智能化的控制[1]。基于对上述问题的考虑,本文设计一种自适应模糊PID控制算法进行在线整定方案。仿真结果表明了该设计下的系统具有良好的动静态性能,较强的鲁棒性[2]。
1 同步传动控制原理
无轴同步传动是指在没有机械主轴的情况下同时实现位置同步和速度同步的控制,输入速度设定值指令,通过控制器来控制变频的驱动器,变频器驱动电机拖动传动机构以带动工作平台运动。检测元件检测两个电机工作平台的位置情况,然后将检测信号反馈到速度补偿器,速度补偿器对两轴位置的误差进行计算,计算结果反馈对副轴进行速度补偿[3,4]。同步控制系统框图如图1所示。
要做到无轴同步传动,首先必须明确位置同步和速度同步两者之间的关系[4]。从数学关系上来看,位置就是速度的积分,而在无轴同步传动控制系统中,所关心的位置差也就是速度差的积分:

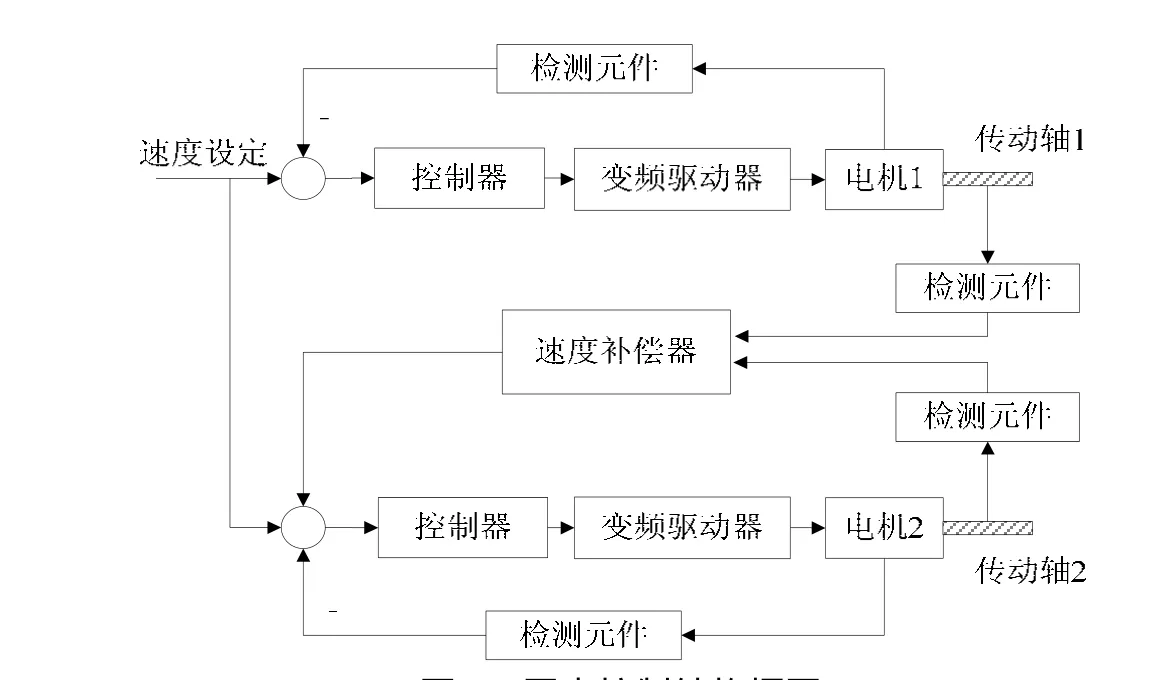
图1 同步控制结构框图
则两轴的速度为:
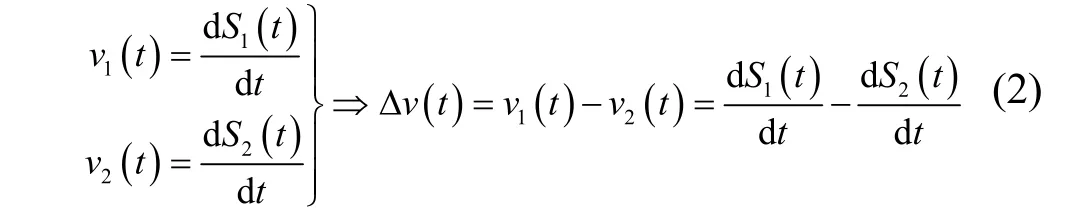
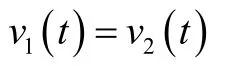
2 自适应模糊PID控制系统设计
2.1 设计思想
传统的同步传动控制思想是用纯PID控制设计的控制器,在实际应用中,系统的动态和静态性能往往不好。本文提出的设计思想是将自适应PID控制与模糊控制理论结合起来,从而构成了自适应模糊PID控制器,自适应模糊PID控制器的控制系统结构图如图2所示,控制系统采用主、从控制方式,两个处于同步运行中的异步电动机在受到不同负载扰动时,运行速度发生变化,系统反馈控制从电机速度跟随主电机速度。在系统中,如果单纯采取选择一个参考模型,让两电动机跟随参考模型变化,两个电动机速度动态过程仍然不一致,同步误差大,满足不了控制的要求。本文采用两个自适应控制器,用控制对象输出的同步误差,同时分别调整两个控制器,达到协调同步的目的。两个控制器自身不但能抑制扰动,还具有相互协调的能力[4]。

图2 自适应模糊PID控制系统结构图
2.2 控制器的设计原理
在实际的同步系统运行中,负载的扰动变化是导致系统不同步的主要原因,我们认为被控对象是时变的,将各种外部扰动看作是模型自身参数的变化[5,6],则有
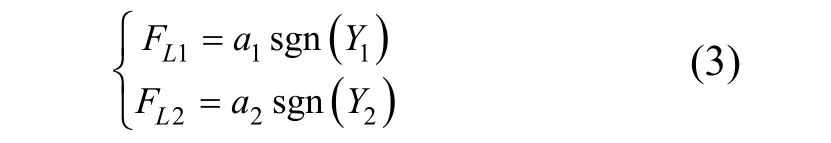
受控对象1的微分方程是:

同理,受控对象2的微分方程是:
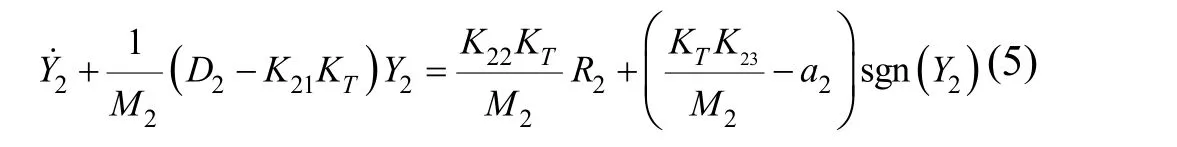
式(5)中Y1、Y2分别是受控对象1和受控对象2的输出;R1、R2分别是受控对象1和受控对象2的输入,且 R1=R2, KT1= KT2=KT
由式(4)、式(5)可以推出系统误差方程如下:
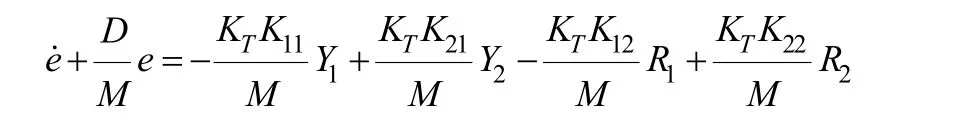


其中

选取Lyapunov(李雅普洛夫)函数[7]

式中iα,iβ为任意的正常数。
对式(10)两边分别求时间的导数,则有

由式(12)可知,V˙是负定的,因此对于任意分段连续且频带较宽的输入函数R,可以保证该自适应控制系统是全局渐进稳定的,即有

2.3 自适应律设计
由式(8)可得
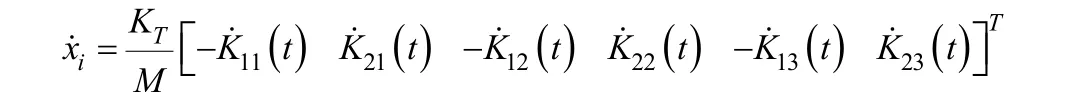
由式(12)可以得出如下的自适应律

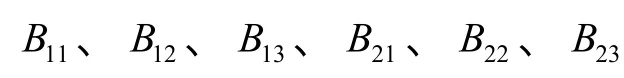
3 仿真及结果分析

在系统起动过程中,同步误差曲线如图3所示。由于两个被控对象的输入为同一给定值,误差并不大。从误差曲线可以看出,两种控制方式误差都不是很大。但是从图中可以明显看出,由于传统PID控制的输出误差曲线波动幅度较大,且调节时间较长。对比来看,自适应模糊 PID控制的误差曲线虽然也有一定的波动,但是波动幅度较小,且很快就可以达到稳定状态。两种控制算法对比效果可以看出,自适应模糊PID控制效果较好。
在系统突加扰动时,同步误差曲线如图4所示。从实验结果可以看出,在系统突加负载扰动的作用下,传统PID控制输出的响应出现了较大的偏差和波动,并且系统动态调节过程较长。比较来看,自适应模糊PID控制输出的响应虽然也有一定幅度的波动,但是并没有出现明显的震荡,且跟随性较好,基本上达到了无轴同步传动控制目标。由于引入自适应模糊 PID控制器进行在线整定,调节系统控制参数,起到了预期的调节扰动的作用,有效地抑制了负载扰动对系统稳定造成的不利影响。
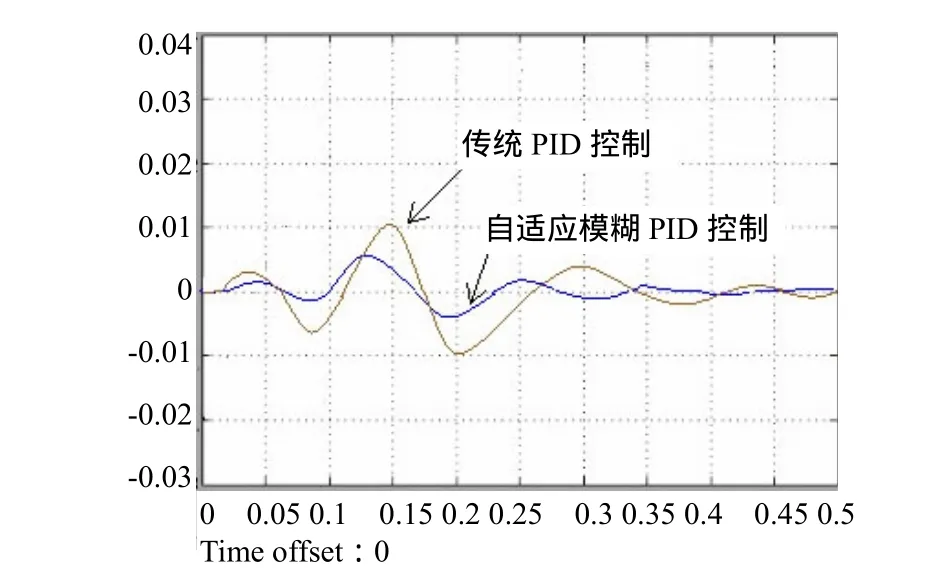
图3 起动过程同步误差曲线

图4 突加扰动过程同步误差曲线
仿真实验结果表明,多电动机无轴同步传动控制系统采用自适应模糊PID控制后,系统的起动过程缩短,能够更快进入稳态运行状态,并且系统误差更小。在仿真实验中,在系统突加相同扰动量的作用下,采用自适应模糊PID控制的系统比采用传统PID控制的系统的抗干扰性有明显的提高,可以最大程度地抑制扰动对系统的影响。因此,基于自适应模糊PID控制的无轴同步传动控制系统具有更理想的动态、静态性能,适合于响应较快、精度要求较高的场合。
4 结束语
在实际的工程项目中,由于工业对象普遍存在着时变性、非线性等不确定性因素,甚至没有准确的数学模型,传统PID控制由于自身的局限性,控制效果一般难以达到理想的效果。模糊控制不使用数值变量描述系统特征,因此就不依赖于被控对象的数学模型,模糊控制用语言变量来描述系统特征,并且根据系统的动态扰动信息,依据模糊控制规则进行模糊推理以获得合适的控制量输出,具有较强的鲁棒性,可以最大程度地抑制扰动。本文提出的自适应模糊PID控制算法充分考虑系统优化过程的特点,把李雅普诺夫稳定性原理和模糊控制理论两种方法结合起来,根据控制对象的实时特征自适应调整控制参数。实现了自适应在线整定控制参数,从而使该算法既有传统PID控制的稳态无静差性,同时还具有模糊控制的快速响应的优点。自适应模糊PID控制可以在系统受到负载扰动时,跟踪调节系统控制参数来抑制扰动,最终达到异步电机无轴同步传动。
[1]张倩倩, 周西峰, 郭前岗. 自适应模糊 PID 控制的异步电机并联运行方法的研究[J].电气传动自动化, 2011(1):15-18.
[2]刘福才,张学莲.多级电机传动系统同步控制理论与应用研究 [J].控制工程,2002,9(4):87-89.
[3]郭庆鼎,唐光谱,唐元钢. 基于自适应控制的双电动机同步传动控制技术的研究[J].机械工业学报, 2002,38(2):79-81.
[4]Leonid Reznik, Omar Ghanayem, Anna Bourmistrov. PID plus fuzzy controller structures as a design base for industrial applications[J].Engineering Applications of Artificial Intelligence,2000,13(4):419-430.
[5]陈庆伟, 郭毓, 胡维礼, 王建侠. 多电机同步联动系统的动力学分析与建模[J]. 东南大学学报(自然科学版), 2004,(S1):135-140.
[6]Tsang, K. M.. Auto-tuning of fuzzy logic controllers for self-regulating processes[J]. Fuzzy Sets and Systems, 2001,120:169–179.
[7]Hassan K Khalil. Nonlinear system [M]. USA:Prentice Hall, 2003.
[8]王辚, 张科. 基于 MATLAB 的自整定模糊 PID控制系统[J]. 探测与控制学报, 2008, 30(2): 73-76.
