四个坐标系下羽毛球飞行运动学模型与仿真

张晶华 汪仁煌 岳洪伟

（广东工业大学自动化学院）

四个坐标系下羽毛球飞行运动学模型与仿真

张晶华 汪仁煌 岳洪伟

（广东工业大学自动化学院）

为使羽毛球飞行的轨迹仿真结果更加真实可靠，构造基于实际环境的羽毛球空间运动状态方程。本文以国产某型号羽毛球制造参数为背景，建立羽毛球球场、羽毛球飞行、羽毛球速度和羽毛球球体4个坐标系，并利用牛顿第二定律等方法直接推导出羽毛球飞行轨迹在这些坐标系下的运动方程。所建立方程不但考虑了空气阻力、羽毛球转动惯量和羽毛球本身参数的影响，还考虑了羽毛球固有旋转特性产生的马格努斯力对其飞行轨迹的影响。仿真结果表明，在四个坐标系下建立的羽毛球运动方程能够直观反映出其相关参数对飞行轨迹的影响。

仿真；四个坐标系；转动惯量；力矩；马格努斯力

0 引言

随着我国社会经济、文化以及体育事业的发展，越来越多的人开始关注体育锻炼。羽毛球运动由于场地不受限制，运动量适合各年龄层次的人，因而深受群众的喜爱。了解羽毛球的特性，掌握羽毛球的飞行轨迹有益于控制球，打出漂亮的球，使得羽毛球运动更具挑战性和欣赏性。目前国内外对羽毛球的研究并不多，主要研究天然羽毛球和塑料羽毛球之间区别的有：文献[1]通过实验测试天然羽毛球和人工塑料羽毛球之间的区别，并用实验结果对比了不同速度下天然羽毛球的空气阻力系数和人工塑料羽毛球空气阻力系数大小关系；文献[2]利用实验研究羽毛球的雷诺系数，并通过实验对比了不同速度和条件下羽毛球雷诺系数与空气阻力系数。关于羽毛球质量检测的研究有：文献[3]利用计算机技术并通过图像处理来检测羽毛球球口是否为圆形的方法，为羽毛球质量检测提出新的途径；文献[4]利用粒子图像测速技术来检测羽毛球旋转是否稳定和左右摇摆，并通过实验给出了一些参数依据，为判断羽毛球质量好坏提供一个标准。关于羽毛球飞行轨迹的研究，目前查到的有文献[5]，在二维平面下，给出了羽毛球在重力和空气阻力作用下的简单质点运动轨迹，并对比了不同速度下天然羽毛球和人工合成羽毛球的飞行轨迹。林传潮[6]叙述了羽毛球在空气飞行中受到的所有阻力以及阻力产生的原因，并通过动量定理给出了羽毛球飞行轨迹，为羽毛球运动员对羽毛球认识从感性上升到理性提供一定的依据。上述有关羽毛球研究的文献只是研究天然羽毛球和塑料羽毛球的区别，或简单地把羽毛球当成一个质点来讨论，并没有对羽毛球的相关参数（如羽毛的马格努斯力），以及羽毛球的固有特性（如旋转等方面的羽毛球飞行轨迹）进行研究。本文对羽毛球飞行实际空间状况、自身组成要素以及自身旋转特性等进行分析和研究，并根据成品羽毛球的实测结果、归纳总结，推导出反映羽毛球实际飞行轨迹的参数方程。

1 羽毛球的马格努斯力产生的原因

羽毛球飞行轨迹除了受空气阻力和本身重力影响外，还受到羽毛球本身固有特性旋转运动产生的影响。由羽毛球的结构特性可知：16根羽毛片按照类似“叶轮”模型组装，羽毛片安装具有一定的攻角，羽毛片在羽毛球的旋转半径的平面内拥有一定的安装角度。因此羽毛球在空气中飞行时，空气流对羽毛球做相对运动，空气流以一定的攻角吹向羽毛球，会在羽毛片上产生摩擦力；又因为羽毛片具有一定的安装角，空气流作用在羽毛片上的摩擦力会在羽毛片切向方向分解一个力，使得羽毛片绕着羽毛球旋转轴旋转。羽毛球在空中飞行既做平移运动又具有旋转现象。

根据马格努斯效应知识，羽毛球在空中飞行时受到与速度方向正交的侧力作用，在此力作用下，羽毛球会偏离原来的轨道，形成一定的弧线轨迹。

根据流体力学知识，羽毛球在飞行过程中，若羽毛球没有旋转，空气流只对羽毛球产生阻力作用，减慢羽毛球的飞行速度；若羽毛球具有旋转，则在旋转和空气粘性作用下，羽毛球周围附面层内会产生环流。在前方回流和环流共同作用下，若空气来流与环流同侧，则空气流加速；反之，则减速。

根据伯努利知识，速度快的一侧，压力下降，速度慢的一侧，压力上升，两侧的压力差对羽毛球侧向产生马格努斯力。

马格努斯力的方向满足右手法则，即拇指指向羽毛球旋转轴（旋转轴方向用右手螺旋法则判断），食指指向羽毛球飞行方向，中指垂直手面，则中指的方向就是马格努斯力的方向。马格努斯力的方向始终和羽毛球飞行速度的方向垂直，因此羽毛球马格努斯力只会改变羽毛球速度的方向并不会改变速度大小，此外由于马格努斯力的方向与羽毛球飞行速度方向垂直，导致羽毛球飞行过程中有一个向心力的作用，可能使羽毛球飞行轨迹发生改变。

羽毛球在飞行过程中，受空气流作用使羽毛球产生旋转，根据以上分析，假设羽毛球上任意部位的旋转角速度是一样的，利用儒可夫斯基环流理论，类似文献[14]推导过程，得到空气流作用在羽毛球上的马格努斯力为：其中，ρ为空气密度；v为羽毛球飞行速度；w为羽毛球的旋转角速度；h为羽毛球的体积；负号代表w的旋转方向，若羽毛球旋转角速度为顺时针旋转，则其符合取负，则此时马格努斯力为正，反之，马格努斯力为负。

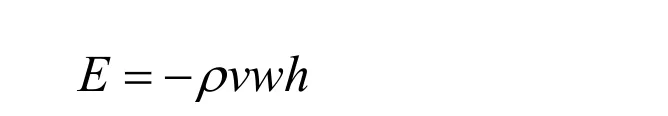
2 羽毛球运动模型

羽毛球在空中飞行的环境既是空间变化的，也是时间变化的，同时羽毛球飞行过程还受本身振动和结构干扰，因此羽毛球飞行过程是一个非常复杂的非线性时变模型。为更加直观表达和描述羽毛球飞行动力学及其飞行轨迹，借鉴文献[15]，建立羽毛球在空间飞行时与自身特性和飞行环境有关的坐标系，即：羽毛球球场坐标系、羽毛球飞行坐标系、羽毛球速度坐标系和羽毛球球体坐标系，这些坐标系之间的坐标变换矩阵为：

1) 羽毛球球场坐标系到羽毛球球体坐标系的坐标变换矩阵

2) 羽毛球球场坐标系与羽毛球飞行坐标系之间的转换矩阵

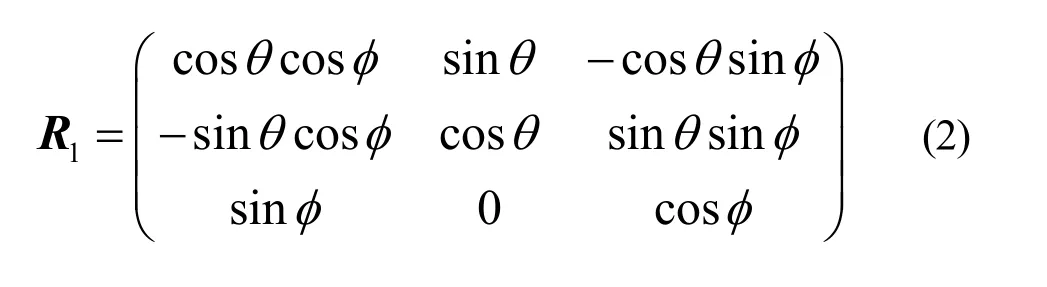
其中θ、φ为旋转角度。

3) 羽毛球速度坐标系与羽毛球球体坐标系之间的转换矩阵

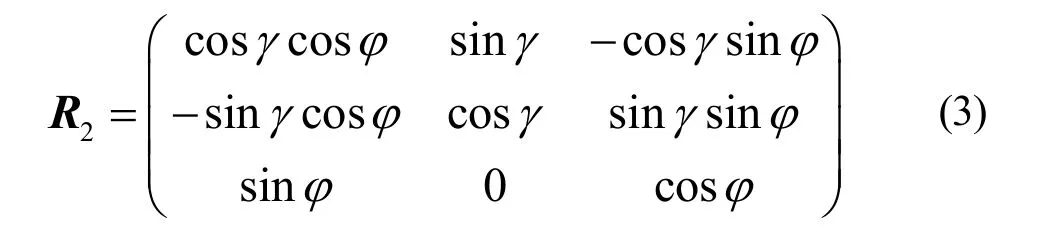
其中γ、φ为旋转变换角度。

4) 羽毛球速度坐标系与羽毛球飞行坐标系之间的转换矩阵

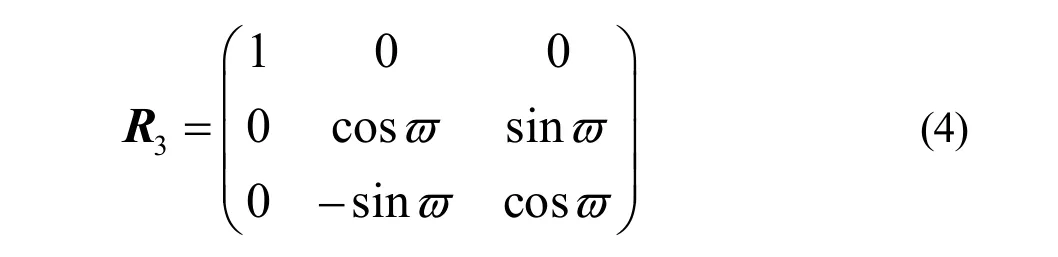
其中ϖ为旋转变换角度。

3 羽毛球飞行运动方程组

假设羽毛球飞行过程中，空气作用在羽毛球上的力使羽毛球稳定旋转而没有产生偏摆，也没有侧面空气来流影响。下面将建立空气作用在羽毛球上的阻力、马格努斯力对其产生的力矩以及坐标变换角度关系的羽毛球运动方程组。

3.1 动力学方程

前面已经建立了羽毛球飞行过程中的所有坐标系，羽毛球的空间运动可以看成是六自由度运动。为便于研究，把羽毛球的矢量方程投影到坐标系。

3.1.1 羽毛球质心运动方程

1) 在羽毛球飞行坐标系中，其动力学方程为：

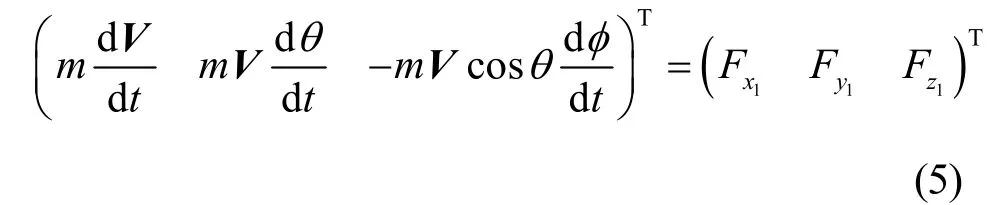
其中，V为羽毛球的速度矢量；dV/dt为加速度在羽毛球飞行坐标系ox1轴上的分量；Vdθ/dt为加速度在羽毛球飞行坐标系oy1轴上的分量；为加速度在羽毛球飞行坐标系oz1轴上的分量；为作用在羽毛球上的力在羽毛球飞行坐标系中各个轴的分力，其由3部分组成：

① 空气作用在羽毛球上的阻力，可以在羽毛球速度坐标系中分解，然后根据式(4)，得到空气作用在羽毛球上的阻力在羽毛球飞行坐标系中的各轴的分力为：

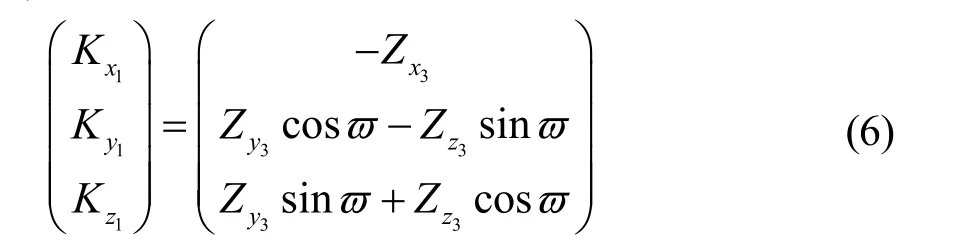
其中，Ki( i=x1, y1, z1)为在羽毛球飞行坐标系中各个轴力的分量；Zj(j=x3, y3, z3)为空气阻力在羽毛球速度坐标系中的分力。

② 羽毛球重力和浮力与羽毛球球场坐标系By轴平行，根据式(3)，可得其在羽毛球飞行坐标系中的分力为：

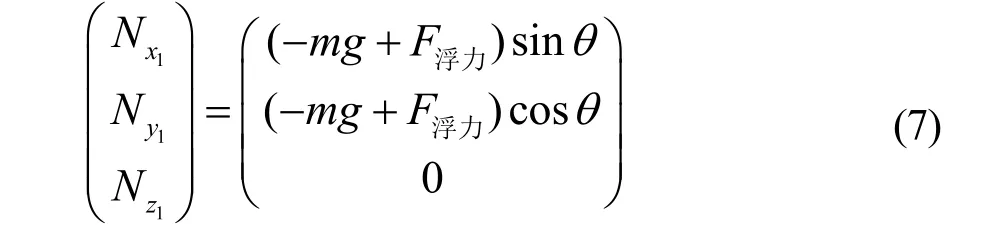
羽毛球的体积约为19立方厘米，其产生的浮力为F=1.86× 10-4(N)，而羽毛球的重力为

浮G=mg=5.488× 10-2(N)，即羽毛球的浮力远远小于羽毛球的重力，因此可以忽略羽毛球浮力对其飞行轨迹的影响。

③ 根据前面的分析，羽毛球产生的马格努斯力与羽毛球球体坐标系中oy3轴重合，根据式(3)、式(4)，可得马格努斯力在羽毛球飞行坐标系中的分力为：

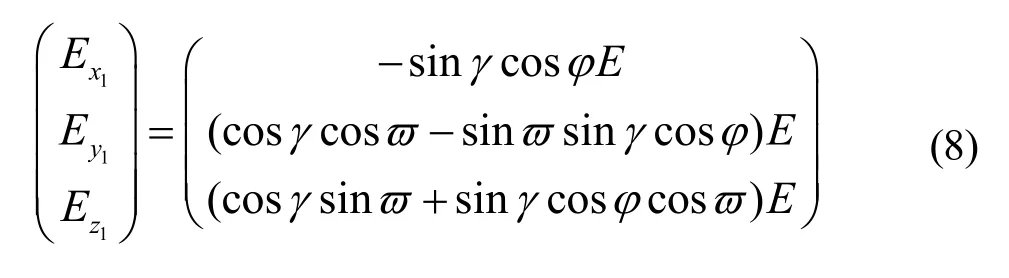
把上式(6)、式(7)、式(8)代入式(5)，从而得到羽毛球的质心动力方程为：

3.1.2 绕羽毛球质心转动的动力学微分方程

绕羽毛球质心转动的动力学方程通常是在羽毛球球体坐标系上建立，根据理论力学刚体对质心的动量矩定理：刚体对质心动量矩的变化率等于所有作用在刚体上外力对质心的矩的主向量为：

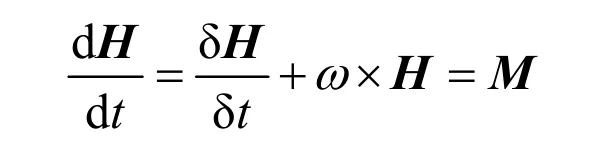
其中，M为空气流对羽毛球的转动力矩；dH/dt、δH/δt 分别为动量矩的绝对、相对导数；H为刚体对质心的动量矩，H=J·ω，其中ω为羽毛球旋转角速度；J为张量（张量与矢量的点积还是矢量），J为惯性矩阵。

3.2 运动学方程

在羽毛球球场坐标系中，羽毛球速度分量为

根据羽毛球飞行坐标系的定义可知，速度矢量V与ox1轴重合，利用转换矩阵可得：

另外，羽毛球在羽毛球球托坐标系绕质心转动的运动方程为：

由此，式(9)、(10)、(11)、(12)和(13)给出了羽毛球的空间运动方程组，它是一个非线性常微分方程组。方程组中所有的参数都跟羽毛球飞行时间有关，它们都是飞行时间的函数。通过式(9)、(10)、(12)和(13)求解，得到结果再代入式(12)求解，从而得到羽毛球飞行轨迹。

4 实验结果与仿真

4.1 羽毛球运动轨迹参数的求解

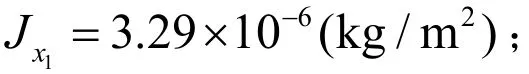
4.2 仿真结果

利用Matlab中Simulink工具箱构造羽毛球六自由度仿真模型，结合上述各个坐标系中所建立羽毛球非线性方程，得到羽毛球飞行三维轨迹如图1所示。

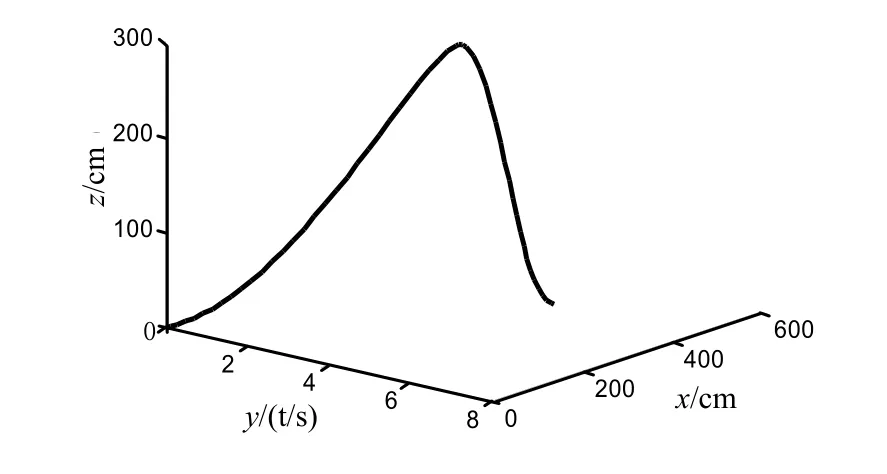
图1 羽毛球飞行轨迹图

羽毛球在水平面o-yz的投影轨迹图如图2所示。

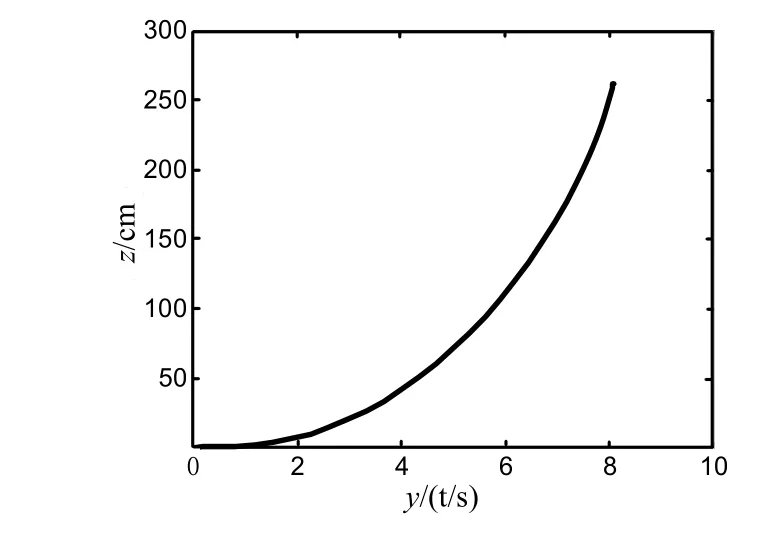
图2 羽毛球飞行轨迹在水平面的投影图

由图2可知，由于飞行过程中受马格努斯力的影响，羽毛球不是对角直线飞行到达落点，而是有一定的弯曲度。

5 结论

文中参照文献[15]坐标系建立方法，给出了羽毛球在四个坐标系下飞行轨迹参数方程，所建立的羽毛球运动模型、羽毛球质心转动模型和气动模型，根据羽毛球的特性以及飞行空间环境进行分析，并结合牛顿第二定律直接对羽毛球受力分析进行直接推导，得到其有关羽毛球自身参数对应的方程组。同时也考虑了羽毛球本身固有旋转特性产生的马格努斯力对其飞行轨迹的影响。仿真结果表明，在所建4个坐标系下，能够直观地反映羽毛球的旋转特性和相关参数对其飞行轨迹的影响。该推理方法较直观，并且可充分利用Matlab的Simulink工具，从而减少编程工作量，同时还具有较好的仿真效果。

[1] Firoz Alam, Harun Chowdhury, Chavaporn Theppadungporn. Measurements of aerodynamic properties of badminton shuttlecocks[J]. Conference of the international sports engineering association , 2010,2(2):2487-2492.

[2] Seigo Kitta, Hiroaki Hasegawa. Aerodynamic properties of a shuttlecock with spin at high Reynolds number[J]. Asia-Pacific Congress on sports technology, 2011(13): 271-277.

[3] 艾星芳,汪仁煌,李雪晨.圆度误差测量在羽毛球外观检测中的应用[J].广东工业大学学报,2011,12(4):51-54.

[4] Kenichi Nakagawa, Hiroaki Hasegawa, Masahide Murakami, et.al. Aerodynamic properties and flow behavior for a badminton shuttlecock with spin at high reynolds numbers[J], Procedia Engineering, 2012(34):104-109.

[5] Julien Le Personnic, Firoz Alam.etc. Flight trajectory simulation of badminton shuttlecocks[J]. Asia-Pacific Congress on sports technology, 2011(13):344-349.

[6] 林传潮.羽毛球空气力学分析[J].中国体育科技,1980(13): 27-33.

[7] 谷嘉锦,陈玉清.羽毛球风洞的设计与应用[J].实验力学，1980,9(3):227-231.

[8] Chen Bingqi, Wang Zhiqiang. A statistical method for analysis of technical data of a badminton match based on 2-D seriate images[J]. Tsinghua Science &Technology, 2007,12(5): 594-601.

[9] Lung-Ming Chen, Yi-Hsiang Pan ,Yung-Jen Chen. A study of shuttlecock’s trajectory in badminton[J]. Journal of Sports Science and Medicine, 2009,77(8):657-662.

[10] Chak Man Chan, Jenn Stroud Rossmann. Badminton shuttlecock aerodynamics: synthesizing experiment and theory[J]. International Sports Engineering Association 2012, 2012,15(2):61-71.

[11] Raveendran Paramesran, Sing Loong Teng. Detection of service activity in a badminton game[J]. IEEE Region 10 Annual International Conference, Proceedings/TENCON, 2011:312-315.

[12] Yoshikawa Fumito,Kobayashi Takumi, Watanabe Kenji, et al. Automated service scene detection for Badminton game analysis using CHLAC and MRA[J], World Academy of Science, Engineering and Technology, 2010(62):942-945.

[13] S L POST, Jordan McLachlan, Travis Lonas, et al. Aerodynamic of a badminton shuttlecock [J]. Proceedings of the ASME 2009 International Mechanical Engineering Congress & Exposition IMECE2009,2009(11):13-19.

[14] 刘大为.球体飞行轨迹异常的探讨[J].大学物理,1987(01): 43-45.

[15] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,1987.

Flight Kinematics Modeling and Simulation of Shuttlecock Badminton Based on Four-Coordinate Systems

Zhang Jinghua Wang Renhuang Yue Hongwei
(School of Automation, Guangdong University of Technology)

In order to make the simulation results of shuttlecock flight trajectory be more reliable, the actual structure of the space environment movement equation of shuttlecock must be constructed. A type of shuttlecock with manufacturing parameters is taked as the research background, its flying track can be deduced by using Newton's second law in a four coordinate space. The established equation not only considers the air resistance, moment of inertia and effects of its parameters, but the inherent rotation characteristics produced by magnus force on the influence of its flight path is also considered. The simulation results show that equation of motion in the four systems of shuttlecock can intuitively reflect the influence of its relevant parameters on the flying track.

Simulation; Four-Coordinate Systems; Rotary Inertia; Moment of Force; Magnus Force

张晶华，男，1981年生，广西玉林人，博士研究生，主要研究方向：图像处理、模式识别等。E-mail: ls198168@163.com

汪仁煌，男，1945年生，上海人，教授，博士生导师，主要研究方向：智能测控、信息处理、智能仪器、机器视觉。

岳洪伟，男，1979年生，安徽毫州人，博士研究生，主要研究方向：图像处理、模式识别。