一种基于压缩感知的信号重建新算法*

2013-07-01乔田田李维国

电讯技术 2013年10期

关键词：线性化广义重构

乔田田,张宇,李维国

(1.中国石油大学(华东)理学院,山东青岛266580;2.哈尔滨理工大学电气与电子工程学院,哈尔滨150080)

一种基于压缩感知的信号重建新算法*

乔田田1,**,张宇2,李维国1

(1.中国石油大学(华东)理学院,山东青岛266580;2.哈尔滨理工大学电气与电子工程学院,哈尔滨150080)

在求解基追踪问题的线性化Bregman迭代方法基础上,结合了广义逆的迭代技术得到一种稀疏信号重构的新算法。该算法在计算Moore-Penrose广义逆时,采用了迭代计算的方式,与算法本身相结合使得仅有矩阵向量乘积运算,避免了奇异值分解的较大工作量。通过数值试验可知,新算法相对线性化Bregman算法在计算时间上约减少了2/3,同时信号的恢复效果也是稳定有效的。因此,新算法是一种有效可行的信号重建算法。

信号重构;压缩感知;广义逆;线性化Bregman迭代法;稀疏重构

1 引言

近年来对有关压缩感知的稀疏信号重构方面的研究越来越受到众多学者的关注。压缩感知是由Donoho[1]等人提出的一种稀疏信号重构的新的信息获取理论,在1998年提出的基追踪模型可以很好地解决稀疏信号重构问题[2]。压缩感知的很多应用领域都涉及到基追踪问题:

式中,A∈Rm×n,f∈Rm,m＜n。

对于问题(1)的求解,在最近几年内得到了迅猛的发展。诸多的研究算法层出不穷,像内点法、梯度投影法等,其中主要是以优化中的Bregman算法的引入继而产生的一系列速度快、效果好的算法为主流,因其相对其他算法在速度上具有明显的优势,使得众多研究者对此兴趣浓厚。Bregman算法是由L.Bregman在1967年提出的优化问题求解中的经典方法[3],最近由Osher[4]等人将其引入图像恢复的应用中得到了前所未有的好结果,提高了图像恢复的计算效率。随即由于Donoho[5]、Candés[6-7]等人在压缩感知方面的进一步工作,使更多的研究者将其引入l1稀疏优化问题当中[8-9]。随着研究的进一步深入,Osher等人提出了带软阈值算子的线性化Bregman方法的一系列的等价形式。由于应用范围的扩大,A的性质不断弱化,方程Au=f很难被满足,于是得到了带有A+的线性化Bregman算法[10]。2010年,张慧等人[11]在此基础上得到了A-的算法,掀开了对特殊矩阵A的稀疏信号重构算法方面更为细致的研究。

本文就是在这些算法研究的基础上,结合之前在广义逆迭代方面取得的成果提出了一种新的混乱迭代算法用以解决稀疏信号重构的问题。

2 预备知识

2.1 广义逆

由于新算法是要结合广义逆的迭代格式,所以在提出新算法之前给出相关的定义和引理。

定义1[12]:设A∈Cm×n,若X满足下面性质,即Moore-Penrose条件:

则称X为A的伪逆,也称作Moore-Penrose广义逆,记作A+。

定义2[13]:设A,B∈Cn×m,称

是(A,B)的值域。

引理1[13]:设A∈Cm×n≠0,如果初始值V0满足

式中,I是m×m单位矩阵,A*是矩阵A的共轭转置。则由

产生的序列{Vq}q∈N收敛到A+。

2.2 线性化Bregman迭代法

用于求解问题(1)的线性化Bregman算法的迭代格式为[8]

k∈N

的唯一解,当μ→∞时,即为问题(1)的极小l2范数解。

与之对应的带软阈值算子的迭代法[9]:

式中,u0=v0=0,且Tμ(·)是软阈值算子[8]。

考虑到A的性质,约束条件Au=f很难满足,文献[8]中提出了A行满秩情况下的式(8)等价的AT算法:

显然,式(9)计算Au=f的最小二乘解。同时考虑到A的条件数太大的影响,得到了A行满秩时等价的A+算法[8]:

对于A是任意矩阵时,文献[11]将其推广至A-算法。从计算的角度,我们看到式(10)既能够得到其最小二乘解,也充分考虑到条件数对计算稳定性的影响,但却由于A+的存在使得计算量加大。

3 新算法

从上节的叙述中可知,A为任意矩阵时,A+算法(式(10))每一步的迭代计算虽然仍为矩阵向量乘积,但A+本身的计算量却很大,且其所需时间也相对较大。因此,为了解决A+计算量大的问题,利用引理1

以及考虑A+计算过程和信号恢复的细节丢失问题,提出了下面的混乱迭代格式:

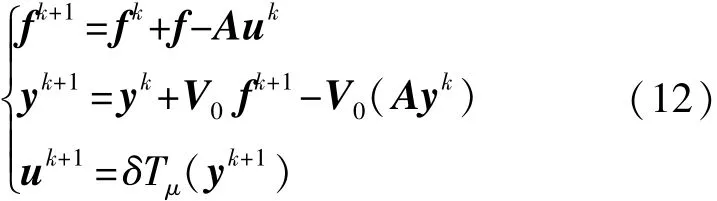
事实上,

即

考虑到式(5)等价于

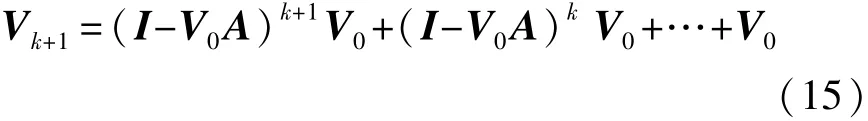
从式(14)、(15)可知,方法(12)是充分考虑到广义逆的迭代技术和使用更多步的细节信息来重建信号,这从使用f0,f1,…,fk+1的数据中可以看出。同时我们还看到,计算量仍能保持仅有矩阵向量乘积的运算,这在速度上依然保持了Bregman系列算法的优势,因此我们有理由相信算法(12)的可行性。下面我们就通过数值试验对比原来的A+算法和改进后的结果来进一步验证我们的推理。

4 数值试验及分析

由于Bregman迭代系列方法取得的快速结果,本文仅在线性Bregman方法的基础上进一步改进,其结果若相对于Bregman系列方法都具有明显优势,则相对经典的一些方法也就不必再加以对比。

数值试验是在Intel(R)Core(TM)2 Duo CPU E7200@2.5GHz 2.5GHz 1.0GB内存的机器上进行的,软件MATLAB7.1版本。

进行随机信号的试验,相同的初值选择u0=f0= 0,A∈Rm×n,V0=α AT,其参数选取采用下面两组:

参数(1)和(2)是分别针对不同量级的信号设定的。从上面的理论讨论可知,0＜δ＜1,μ取相对较大的数,这里我们为了对比结果一致选取10(可以参见文献[9])。由于采用是相对量级上的随机信号进行的实验,所以具有一般性,算法不受实际信息环境的影响。实验结果也是随机的,数据分析具有一般性,数据结果的对比状况基本一致。其中,我们还注意到参数(1)的随机实验,其矩阵条件数为cond(A)=2.054330337102665e+016,而参数(2)则达到cond(A)=1.792691288210052e+017,由此可见,尽管矩阵是病态的情况下,算法的恢复效果仍然是稳定的。

图1和图2是在参数(1)条件下,绘制的原始信号、测量信号以及两种方法分别恢复的结果;图3和图4是在参数(2)条件下,对应的上述信号的图像。表1中显示在不同参数条件下,两种算法的对比结果。在同一误差量级的情况下,我们可以看到计算时间大约减少了2/3,并且随着计算规模的增加,混乱迭代算法呈现出更为明显的优势。同时,注意到A的条件数巨大,说明计算问题是病态的。而且rank(A)＜＜m＜n,信号数目非常稀疏的情况下,我们采用混乱迭代算法仍能很好地替代A+的计算取得满意的结果,说明该算法的确很有竞争力,具有较好的恢复效果。

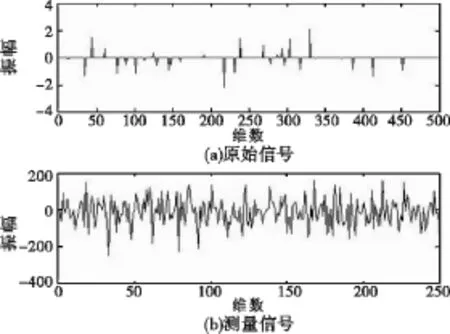
图1 原始信号和对应的测量信号(n=500,m=250)Fig.1 Clear and measurement signal when n=500,m=250

图2 恢复信号(n=500)Fig.2 Restored signals when n=500

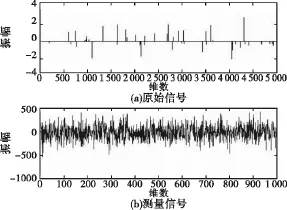
图3 原始信号和对应的测量信号(n=5 000,m=1 000)Fig.3 Clear and measurement signal when n=5 000,m=1 000

图4 恢复信号(n=5 000)Fig.4 Restored signals when n=5 000

表1 不同参数下两种算法的计算结果对比Table 1 Two algorithm calculation results under different parameters

5 结论

从上面的分析中可以看到,本文提出的基于线性化Bregman迭代方法和广义逆迭代技术的新算法在求解基追踪问题时,是非常有效的。它具有线性化Bregman迭代法的全部优点,还在计算耗时和工作量上具有较大的优势。从理论分析可知,该方法更多地考虑数据信息细节丢失的影响,利用更多的数据信息,从而使稀疏信号重构的效果得以提高,是在本质上提高重构的效果。从数值试验的结果分析可知,信号数据都是随机产生的,同时在试验过程中也并未发现有任何例外的情况,因此结论具有一般性。下一步应可以考虑更为细微的信号的恢复情况,进一步增强信号恢复的准确性。

[1] Tsaig Y,Donoho D L.Extensions of compressed sensing [J].Signal Processing,2006,86(3):549-571.

[2] Chen S S,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61.

[3] Bregman L M.The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming[J].USSR Computational Mathematics and Mathematical Physics,1967,7 (3):200-217.

[4] Osher S,Burger M,Goldfarb D,et al.An iterative regularization method for total variation-based image restoration[J].Multiscale Modeling&Simulation,2005,4 (2):460-489.

[5] Donoho D L.Compressed sensing[J].IEEE Transac

tions on Information Theory,2006,52(4):1289-1306. [6] Candès E J,Romberg J.Quantitative robust uncertainty principles and optimally sparse decompositions[J]. Foundations of Computational Mathematics,2006,6(2): 227-254.

[7] Candès E J,Romberg J,Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.

[8] Yin W,Osher S,Goldfarb D,et al.Bregman iterative algorithms for l1-minimization with applications to compressed sensing[J].SIAM Journal on Imaging Sciences, 2008,1(1):143-168.

[9] Cai J F,Osher S,Shen Z.Linearized Bregman iterations for compressed sensing[J].Mathematics of Computation, 2009,78(267):1515-1536.

[10] Cai J F,Osher S,Shen Z.Linearized Bregman iterations for frame-based image deblurring[J].SIAM Journal on Imaging Sciences,2009,2(1):226-252.

[11] 张慧,成礼智.A-线性Bregman迭代算法[J].计算数,2010,32(1):97-104. ZHANG Hui,CHENG Li-zhi.A-linearized Bregman iteration algorithm[J].Mathmatica Numerica Sinica, 2010,32(1):97-104.(in Chinese)

[12] Wang G,Wei Y,Qiao S.Generalized Inverses:Theory and Computations[M].Beijing:Science Press,2004.

[13] 王松桂,杨振海.广义逆矩阵及其应用[M].北京:北京工业大学出版社,1996:202-209. WANG Song-gui,YANG Zhen-hai.Generalized Inverse Matrix and its Application[M].Beijing:Beijing Industrial University Press,1996:202-209.(in Chinese)

QIAO Tian-tian was born in Suihua,Heilongjiang Province,in 1983.She is now a lecturer and currently working toward the Ph.D. degree.Her research concerns image and signal processing.

Email:qtthsnxf@126.com

张宇(1988—),女,黑龙江大庆人,硕士研究生,主要从事电力电子方面的研究;

ZHANG Yu was born in Daqing,Heilongjiang Province,in 1988.She is now a graduate student.Her research concerns power electronics.

李维国(1964—),男,山东临沂人,教授、博士生导师,主要从事数值计算与图像处理方面的研究。

LI Wei-guo was born in Linyi,Shandong Province,in 1964. He is now a professor and also the Ph.D.supervisor.His research interests include numerical computing and image processing.

A New Signal Reconstruction Algorithm Based on Compressed Sensing

QIAO Tian-tian1,ZHANG Yu2,LI Wei-guo1
(1.College of Science,China Universityof Petroleum,Qingdao 266580,China; 2.College of Electrical and Electronic Engineering,Harbin University of Science and Technology,Harbin 150080,China)

Combined with the iterative method of generalized inverse,a new algorithm for sparse signal reconstruction is developed based on linearized Bregman iteration for solving the basis pursuit problems.During calculating Moore-Penrose generalized inverse,the algorithm only has the matrix-vector multiplication by iteration combined with its own,so that the singular value decomposition(SVD)is avoided.The numerical experiments show the computation time has reduced by about 2/3 than that of original algorithms. Meanwhile,the recovery of signals is stabe and effective.So this new algorithm is a feasible signal reconstruction algorithm.

signal reconstruction;compress sensing;generalized inverse;linearized Bregman iteration; sparse reconstruction

The National Natural Science Foundation of China(No.61101208);The Fundamental Research Funds for the Central Universities(13CX02086A);The Innovation Fund of Oceanic Telemetry Engineering and Technology Research Center,State O-ceanic Administration(2012003)

date:2013-05-31;Revised date:2013-09-25

国家自然科学基金资助项目(61101208);中央高校基本科研业务费专项资金(13CX02086A);国家海洋局海洋遥测工程技术研究中心创新青年基金项目(2012003)

**通讯作者:qtthsnxf@126.com Corresponding author:qtthsnxf@126.com

TN911

1001-893X(2013)10-1289-04