桥梁桩基模拟的简化方法及应用
2013-06-29刘中田
刘中田
(同济大学建筑设计研究院(集团)有限公司,上海市 200092)
0 前言
对于弯梁桥、刚构桥、斜拉桥等桥型结构需要考虑下部桩基的弹性约束作用,才能求解体系的真实内力和位移。因此如何较为准确、简便的模拟桩-土相互作用,是广大桥梁设计人员需要面对的一个技术难题。目前工程上常用的桩基模拟方法有刚度系数法、比拟杆件法、等代梁单元法[1-3]。以上三种方法均需先求解桩-土相互作用的刚度矩阵(或柔度矩阵),若不借助专门的计算程序很难实现。本文通过理论推导,给出了一种便于手算、易于直观理解的简化模拟方法,并通过实际算例对简化计算方法的精度进行了验证,该方法可以满足工程需要。
1 桩基的模拟方法
当仅考虑平面问题时,桥梁下部桩基与土的相互作用形式可以用刚度矩阵的形式表示:
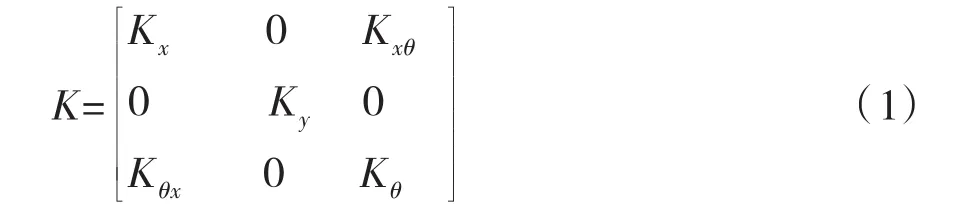
刚度矩阵K中存在四个相互独立的刚度系数[1]:Kx(水平刚度系数)、Ky(竖直刚度系数)、Kθ(转动刚度系数)、Kxθ(Kθx弯剪刚度系数)。等效的计算模型能否准确模拟桩基与土的相互作用,关键在于模型能否反映上述四个刚度系数。目前工程上常用的模拟方法有以下三种:(1)刚度系数法;(2)比拟杆件法;(3)等代梁单元法,见图1。
1.1 刚度系数法

图1 基础模拟图
该方法主要应用于通用的有限元程序中,如Midas、桥梁博士等软件预留有弹性边界条件的接口,可以将四个刚度系数输入到计算模型中。但也有一些计算程序未提供弹性边界条件接口,或者接口参数不全(如QJX未提供弯剪刚度参数),就无法精确应用此方法。
1.2 比拟杆件法
比拟杆法将桩基模拟为一个墩底固结的双柱式框架,其横梁的抗弯刚度EI为无穷大,框架柱截面宽为a、截面高为b,柱高为h、柱间距为c,共四个参数对应于四个刚度系数,可建立正定线性方程组进而求出唯一解。现行桥梁设计规范中给出了比拟结构参数的详细计算公式。双柱式框架只适用于二维平面问题,对于空间问题由于存在七个独立的刚度系数(忽略扭转刚度),理论上则需要具有七参数的比拟结构来模拟,目前尚未见到有实际工程应用。
1.3 等代梁单元法
等代梁单元法采用单个空间梁单元与一根竖向弹簧串联的方式来模拟下部结构,等代结构中共有梁单元截面宽度、截面高度、单元长度及竖向弹簧刚度四个参数,从而与桩基础建立唯一的等代关系。本方法也仅适用二维平面问题。
以上三种方法均需先求解桩-土相互作用的刚度矩阵,然后再进行等代计算,对于大多数桥梁设计人员来说既复杂又不易直观判断。
2 简化计算方法
2.1 简化计算思路
本文对等代梁单元法进行简化处理,将每根桩均等代为与桩基直径相同的梁单元同竖向弹簧串联的形式,对单桩和群桩均适用,见图2、图3,因此本方法可用于平面及空间问题分析。由于等代结构中只有桩基等代长度L和竖向弹簧刚度Ks两个参数,从理论上讲简化后的模型与桩基础并不能完全等代。但如果等代误差能控制在工程可接受的范围之内,本方法就不失为一个可行的解决途径。下文将重点介绍L和Ks的推导过程,并对本方法进行误差分析。
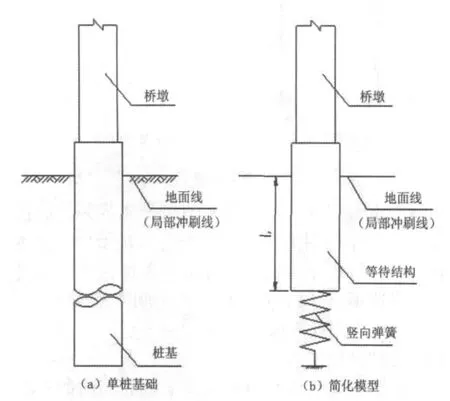
图2 单桩模拟图
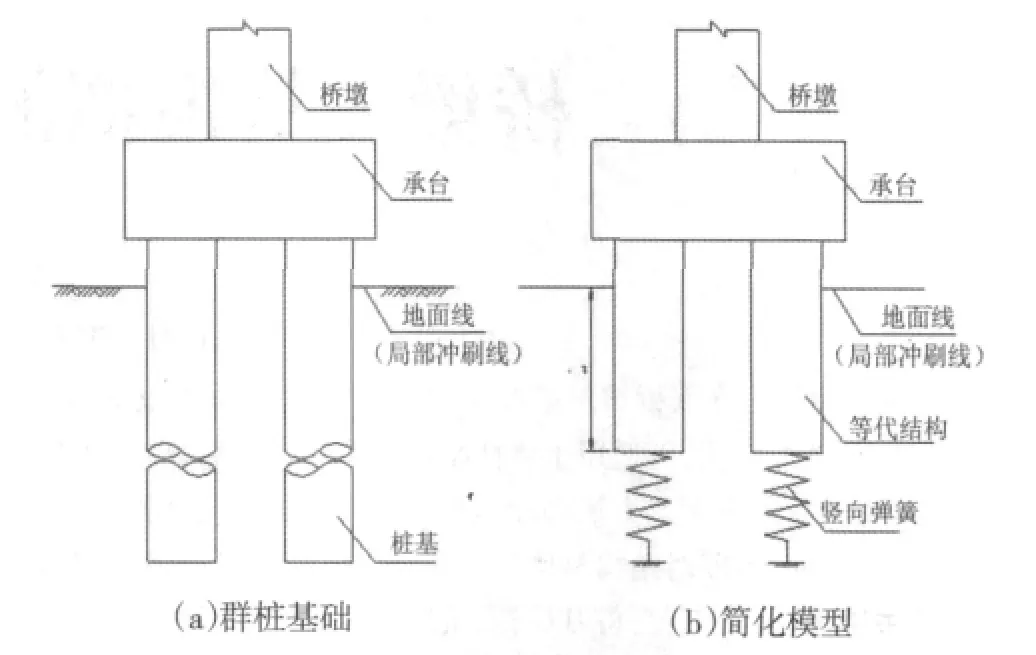
图3 群桩模拟图
2.2 桩基等代参数的推导
由《公路桥涵地基与基础设计规范》(JTGD63-2007)附录P,求出单根桩在地面线(或局部冲刷线)处的柔度系数如下:
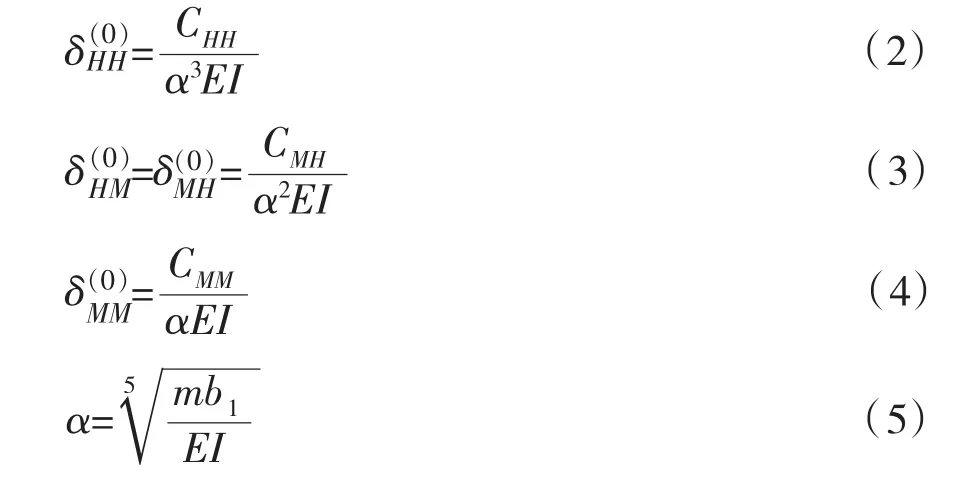
上述公式中系数CHH、CMH、CMM可由规范查表计算得出,α的计算与规范相同。
对于等代结构(见图4),也可求出在地面线(或局部冲刷线)处分别作用单位水平力和单位弯距时的柔度系数:
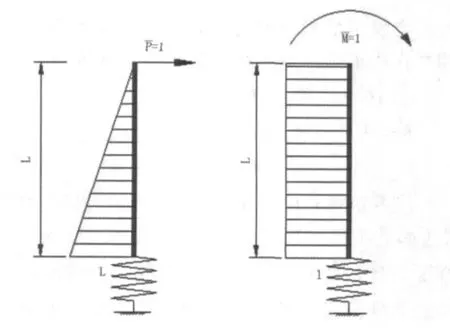
图4 等代结构弯距图


式中:C为等代结构的桩长等代系数。对于地面线(或局部冲刷线)以下桩长为h的摩擦桩或嵌岩桩,由式(2)~ 式(10)可分别求出 αh=(2.5~∞)时对应的等代系数C,并求出L1、L2、L3相对于的误差,见图5~图7。
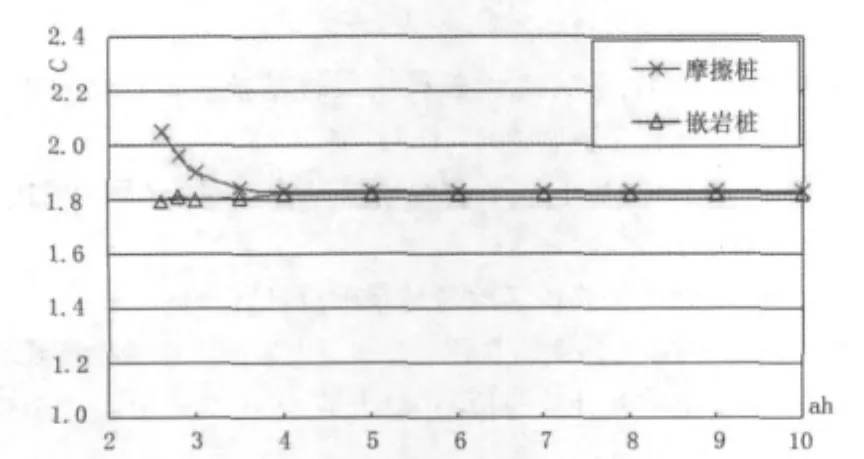
图5 C与ah的关系曲线

图6 摩擦桩等代误差曲线
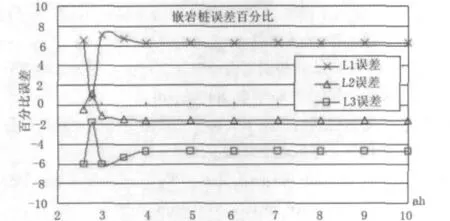
图7 嵌岩桩等代误差曲线
对于摩擦桩,当ah=2.5时C值为2.1,当ah=4时等代系数C达到稳定值1.83。L1、L2、L3相对于L的误差在6.5%以内,该误差分别反映等代结构与实际桩基础水平、弯剪耦合及转动三个自由度的近似程度。
对于嵌岩桩,当 ah≥2.5 时 C 值为 1.82,L1、L2、L3相对于L的误差在7.5%以内。
由于实际工程中摩擦桩均为中、长桩,ah大于4,因此摩擦桩及嵌岩桩的桩长等代系数C可统一取为1.82,此时等代模型与实际结构的误差可控制在7.5%以内。即得到简化计算模型的等代长度公式如下:

2.3 桩底竖向弹簧刚度Ks的推导
由《公路桥涵地基与基础设计规范》,可求出单根桩在地面线(或局部冲刷线)处作用单位轴向力时的位移:

同样可以求出图2中的等代模型,在地面线(或局部冲刷线)处作用单位轴向力时的位移:

式(12)与式(13)联立可求出等代结构竖向弹簧刚度Ks:

3 计算实例
对某高桩承台进行抗船撞受力分析,承台顶竖向力为25 000 kN,水平船撞力3 000 kN作用位置在承台顶面以上2 m处。承台尺寸6.6 m×6.6 m×2.5 m,采用4Φ1.8 m的嵌岩桩,桩间距3.6 m,承台底标高0.0 m,桩底标高-35 m;承台采用C30混凝土,桩基采用C25混凝土。局部冲刷线标高-8 m,其下共有3层土层分别为:淤泥质粘土,层厚6 m,比例系数m为4 000 kN/m4;亚粘土,层厚9 m,比例系数m为8 000 kN/m4;砾砂层,层厚7 m,比例系数m为30 000 kN/m4;基岩面标高-30 m,岩石地基抗力系数C0为3×106kN/m3。
根据式(5)可求出 α=0.239,代入式(11)求出等代桩长L=7.615 m,并由式(14)求出竖向弹簧刚度Ks=2 610 000 kN/m。等代模型参数全部计算得出。
为了验证简化计算方法的准确性,与比拟杆件法计算结果进行对比。由地基规范及桥梁规范可以求出比拟杆件的计算参数:截面宽a=0.924 m,截面高b=2.287 m,柱高h=15.514 m,柱间距c=3.622 m。结果比较见表1。
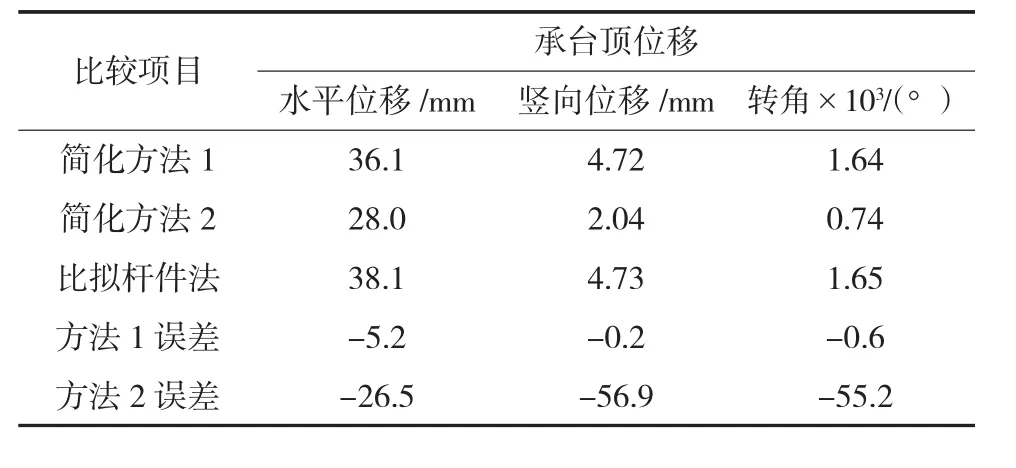
表1 简化计算方法与比拟杆法结果比较
简化方法1考虑竖向弹簧刚度,简化方法2不考虑。方法1与比拟杆件法误差最大为5.2%,其中水平位移相对于竖向位移和转角误差略大,与图7中误差分析结果一致。方法2误差较大,说明竖向刚度对结构整体受力影响显著,需要引起桥梁设计人员的重视。
本方法等代结构与原桩基截面尺寸相同,对于高桩承台,等代结构的桩顶内力即为结构的真实受力状态,可以直接进行配筋计算,这也是本方法的一个优点。
4 结语
(1)本文推导给出了一种桩基模拟的简化计算公式,该公式计算简便且易于理解,可用于桥梁平面及空间问题分析[4]。
(2)通过与比拟杆件法进行对比,文中推荐的简化方法精度较高,且对于高桩承台可以直接求解桩顶内力。
(3)在桩-土结构相互作用分析时,桩基竖向刚度对结构整体受力的影响较为显著,应引起桥梁设计人员的重视。
(4)本文公式是在“m”法线弹性地基梁的假定下推导得出的,如何求解非弹性状态的桩基模拟方法还有待进一步研究[5]。
[1]史福明,刘宏瑾.桩基础结构中分析计算的若干问题[J].桥梁建设,1996(3):67-73.
[2]刘华,叶见曙.桥梁桩基的模拟与计算[J].苏州科技学院学报,2004(2):46-50.
[3]丁兆铭,王立新.刚性墩台桩基础的等刚度模拟[J].水利水电科技进展,1999(4):34-36.
[4]刘伟岸,叶爱君,王斌斌.大跨径桥梁桩基抗震简化模型的分析和探讨[J].结构工程师,2007(1):51-55.
[5]胡春林.胡胜刚.基于P~Y曲线的桩基内力及变形分析[J].土工基础,2006(1):45-48.
[6]JTG D63-2007,公路桥涵地基与基础设计规范[S].
[7]JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
[8]赵明华.桥梁桩基计算与检测[M].北京:人民交通出版社,2001.
