“整体法”在微积分计算中的应用*

何少芳，邹锐标

(湖南农业大学理学院，湖南 长沙410128)

在微积分的计算中，有函数求极限、求导数与微分及求不定积分等重要运算.其中，在函数求极限的方法中，应用两个重要极限、等价无穷小替换、幂指函数的恒等式法求未定式极限时，利用“整体法”对以上方法进行拓展，用更直观、更容易理解的形式体现，可使我们在求函数极限时更简便、快捷;在求导数及微分的运算中，应用“整体法”将基本求导公式拓展，有利于我们对复合函数求导法及函数一阶微分形式不变性的掌握;在求不定积分的运算中，利用“整体法”将基本积分公式延展，能使我们对求不定积分的第一类换元法理解得更深刻，从而更容易掌握求不定积分的第一类换元法.

1 “整体法”在函数求极限中的应用

1.1 利用两个重要极限求函数极限

1.2 利用等价无穷小替换求函数极限

当x→0时，将常用的等价无穷小量中的x看成一个整体Δ，得到拓展后的常用等价无穷小，如当Δ→0时，有sinΔ等价于Δ，arc sinΔ等价于Δ，ln(1+Δ)等价于Δ，利用这些“整体化”后的等价无穷小量，使得求函数极限运算更方便.

1.3 “整体法”在幂指函数未定式求极限中的应用

在恒等式x=elnx中，利用“整体法”将等式中的x看成一个整体Δ，有恒等式Δ=elnΔ，从而幂指函数有恒等式［f(x)］g(x)=eg(x)lnf(x)，当幂指函数［f(x)］g(x)是 1∞，00，∞0三种未定式时，g(x)lnf(x)是0*∞ 型未定式，将其转化为，或型未定式，则可考虑用洛必达法则求出函数的极限.

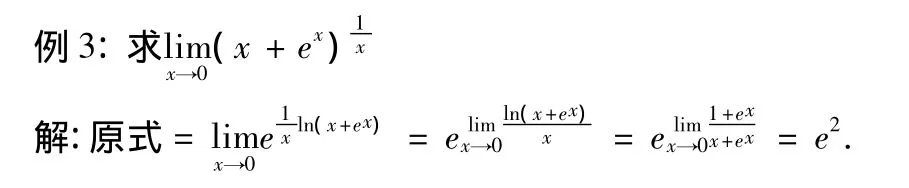
2 “整体法”在求导数及微分中的应用

在复合函数求导法中有定理［2］:如果u=g(x)在点x处可导，而y=f(u)在点u=g(x)可导，则复合函数y=f(g(x))在点 x 处可导，且求导数为 y′=f′(u)*g′(x).我们将定理中的u=g(x)看成一个整体，y=f(u)是“整体”u=g(x)的函数，则有“整体法”求导公式［f(Δ)］′=f′(Δ)* Δ′.由此，我们利用“整体法”可将基本求导公式延拓，如 (Δn)′=n* Δn-1* Δ′，(aΔ)′=aΔ*lna* Δ′.同理，在一阶微分形式不变性中，也可利用“整体法”得到微分公式dy=f′(Δ)dΔ(不论Δ是x还是x的函数等式都成立).

3 “整体法”在不定积分计算中的应用

在求不定积分方法之第一类换元法中，有定理［2］:已知∫f(u)du=F(u)+C，u= φ(x)可导，则有换元公式∫f(φ(x))φ′(x)dx=f(φ(x))dφ(x)=F(φ(x))+C.我们将定理中的u=φ(x)理解为一个整体Δ，则有换元公式∫f(Δ)dΔ =F(Δ)+C，由此可将基本积分公式“整体化”为+C等.

4 小结

“整体法”并非是微积分运算中的新方法，只是在求极限、求导数与微分、求不定积分运算中，将其运算方法的理论依据(即相关定理)用更直观、更形象的方式来表达，并将其中用到的方法及基本求导公式、求积分公式进行拓展.“整体法”这种更容易理解和接受的表现形式，能使我们对运算方法的相关定理理解得更透彻，同时在微积分的计算中对这些运算方法的使用更加灵活自如.

［1］邹锐标，姚平贵.高等数学［M］.北京:中国农业出版社，2011.

［2］同济大学数学系.高等数学(第六版)［M］.北京:高等教育出版社，2007.