基于Matlab的达能饼干销量预测分析*

罗佳佳

(南华大学附属第二医院，湖南衡阳421001)

预测分析是数据挖掘的一个重要任务.预测的目的是从历史数据中自动推导出对给定数据的推广描述，从而能对未来数据进行预测［1］.Matlab是一个高级的数值分析、处理与计算软件，广泛应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域.

本文收集达能饼干的销售数据，使用MATLAB对收集的数据进行数据拟合，建立回归预测模型，对未来销量做出预测，以便挖掘出有价值信息反馈给管理者和决策者.

1 数据收集

1.1 研究对象

研究在学生中销量很大的饼干.选取“达能”作为此次研究的主体对象，选取“奥利奥”作为同类商品.并假设“达能”饼干的销量主要与同类产品的价格以及广告投入有关.

1.2 收集数据及整理数据

根据代理商提供的原始数据，标准化奥利奥的价格，得到整理后数据.表1中“125G奥利奥饼干单价”是由“150G奥利奥饼干单价”换算过来的，比较“125G奥利奥饼干单价”与“125G达能饼干单价”，“奥利奥”的平均价格高出约0.2元，表1中的“125G奥利奥饼干标准单价”就是由“125G奥利奥饼干单价”减去0.2得来的.经此处理，达能和奥利奥就存在竞争关系了.

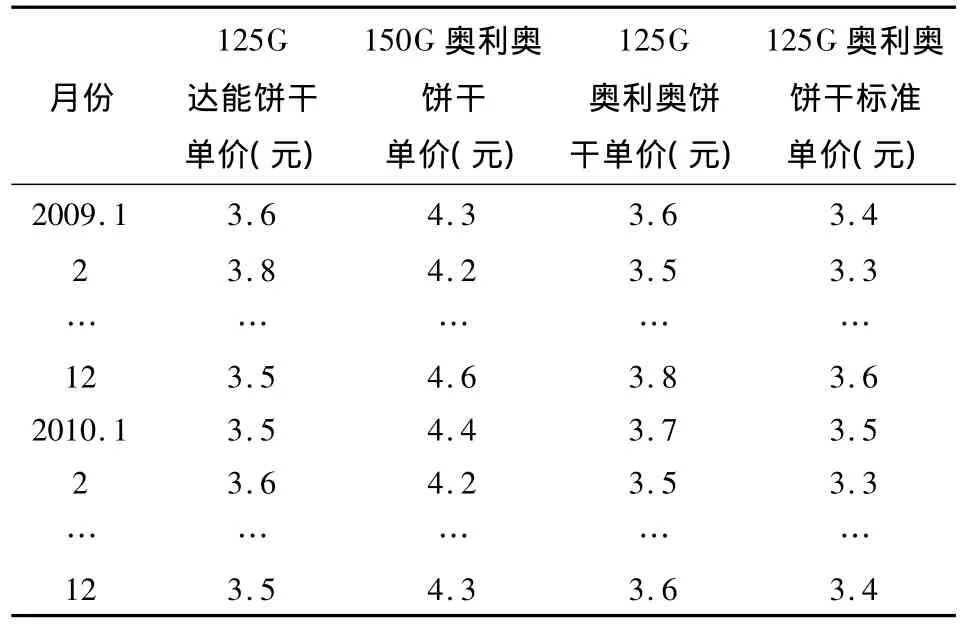
表1 2009－2010年达能饼干与同类产品单价的原始数据

2 模型的假设与建立［2］

2.1 模型的假设

通过之前的分析，假设影响“达能”饼干销量的主要因素是与同类产品的差价以及广告投入，于是得下表2.

表2 2009－2010年达能饼干与同类产品差价、广告投入及销量

令，y－达能饼干的销量;x1－达能与奥利奥饼干的差价;x2－达能饼干的广告投入;分别将x1和x2与y在MATLAB进行数据拟合，从图1、图2可以发现x1与y近似线性相关，x2与y近似二次相关.

图1 达能饼干销量与同类饼干差价比较

使用多元线性回归模型y=β0+β1x1+ε来拟合饼干销售量随饼干与同类饼干差价的变化.

使用多元线性回归模型y=β0+β1x2+β2x+ε来拟合饼干销售量随饼干广告投入的变化.

图2 达能饼干销量受广告投入影响

2.2 模型的建立

假设x1和x2与y之间有多项式回归关系，建立模型:y= β0+β1x1+β2x2+β3x+ε，其中，y为被解释变量(因变量);x1，x2为解释变量(回归变量，自变量);β0，β1，β2，β3为回归系数;ε为随机误差(均值为0的正态分布随机变量).

3 模型的求解与检验［3］

3.1 模型的求解

使用MATLAB统计工具箱，输入命令:

(其中alpha为显著性水平，缺省时为0.05)

输出的结果为:

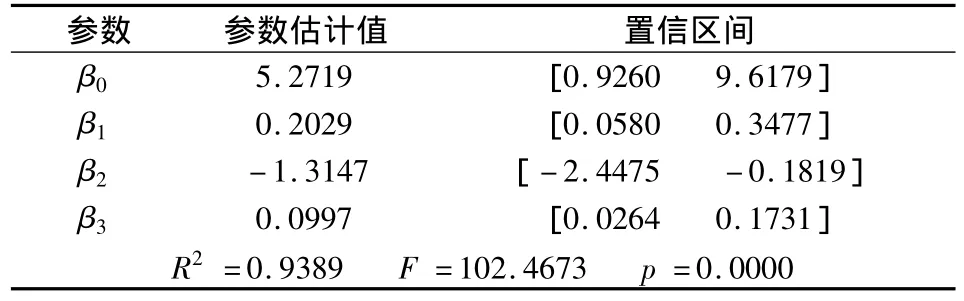
参数 参数估计值 置信区间β0 5.2719 ［0.9260 9.6179］β1 0.2029 ［0.0580 0.3477］β2 －1.3147 ［－2.4475 －0.1819］β3 0.0997 ［0.0264 0.1731］R2=0.9389 F=102.4673 p =0.0000

3.2 模型的检验

R2=0.9389说明y的93.89%可由模型确定;而F远超F检验的临界值，故也认为模型拟合度优秀，事实上，F=，说明F与R2检验等效;p值是与F对应的概率，由于p远小于α(α =0.05)，故回归模型成立.再观察参数的置信区间，均不包含0点，说明模型很好地符合了实际情况.

4 模型的分析与预测

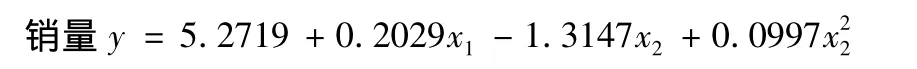
从函数关系可以看出，价格优势可以增加销量，增加广告投入亦可以增加销量.

差价x1=奥利奥饼干价格x3－达能饼干价格x4

我们欲控制x1的值来达到较为理想的销量.在实际操作中，可以根据估计x3的值来确定x4的值.现在我们控制差价x1=0.2 元，广告投入 x2=8.1 万元.

在MATLAB中输入命令:

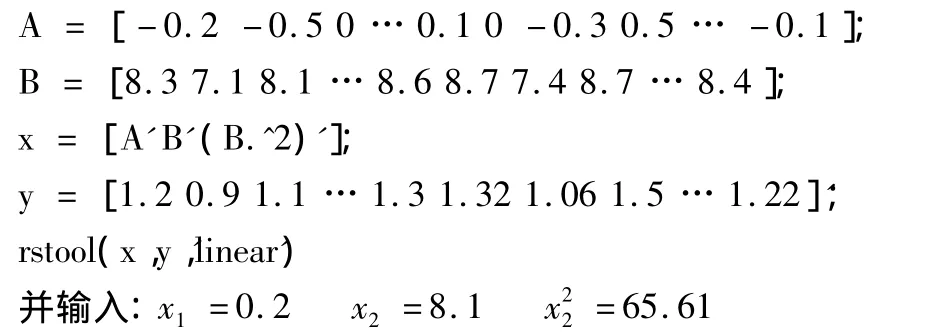
得到在此条件下y的销量:

销售量的预测区间为［1.2071 －0.0900，1.2071+0.0900］(置信度 95%)，即预测销量的范围在［1.1171，1.2971］之间(置信度95%).

实际应用中，我们可以把上限12.971万筒作为库存管理的目标值，而把下限11.171万筒用来把握公司的现金流.若估计x3=3.5，设定x4=3.3，则有95%的把握知道销售额在3.3 × 11.171=36.8(万元)以上.

根据模型的预测，可以看出:达能饼干的销量与同类产品的价格优势关系密切，且价格与销售量的大小呈现负相关，说明适当的价格优势可以增加饼干的销量;而饼干销售量和广告费用的投入呈现正相关，说明适当的增加饼干的广告投入可以增加商品的销售.适当保持价格优势和提高广告投入，达能饼干的销售量将得到保证.

5 结语

统计中的回归分析最主要的应用是用来预测，考虑饼干的价格变化不是很大，本文采用的预测数据是近两年代理商提供的直接数据，借助Matlab强大的矩阵处理能力，实现了达能饼干销量的有效预测分析.

［1］孙雷.回归技术在超市商品销售趋势预测模型中的应用［J］.江苏广播电视大学学报，2008，(5):51－53.

［2］刘锋.数学建模［M］.南京:南京大学出版社，2005.

［3］张宜华.精通 MATLAB5［M］.北京:清华大学出版社，1999.