城市路内停车设施选址优化模型*

杨启福

(长沙理工大学交通运输工程学院，湖南长沙410076)

随着城市机动化水平的不断提高，城市交通问题越发凸显.停车问题已成为城市交通管理面临的重大课题.路内停车场是指在道路用地以内划定的允许车辆沿道路的一侧或两侧停放的场所［1］.许多学者对路内停车的相关问题进行了研究，取得了一系列成果:梅振宇等［2］通过定量分析影响路内停车需求及供给的因素，建立了路内停车的宏观比例优化模型.王姝春等［3］通过研究路内停车的行为特点及路内停车对动态交通的影响，提出了一种考虑与路外停车相协调的路内停车选址模型.梁军等［4］通过分析路内停车存在的问题，从路内停车对机动车和非机动车的横向驾驶行为产生的影响和路内停车对交通运行效率的影响两个方面对路内停车对动态交通的影响进行了研究.

本文通过分析影响路内停车场供给和需求的因素及路内停车场布局规划需要考虑的因素，建立了一个路内停车泊位选址优化模型，为相关部门进行停车设施规划与管理工作提供参考和决策支持.

1 建模思路

1.1 路内停车需求与供给影响因素分析

路内停车需求的影响因素复杂，难以完全进行定量描述.通常选取某些较为显著的因素进行分析.引起城市路内停车需求变化的因素主要有:城市功能分布和土地运用情况、城市的经济发展水平、机动车保有量和结构、机动车出行水平及出行特征、城市配建停车设施和停车需求管理政策等.而路内停车设施的供给能力则主要由城市区域的道路网络状况、道路技术等级、道路上交通流运行状况等因素决定.

1.2 路内停车设施选址的影响因素分析

本文在构建路内停车设施布局选址模型时，考虑了研究区域内停车设施的供需状况，考虑了泊车者的走行距离即规划的路内停车设施与停车需求点间的距离，规划路内停车设施的数量和设施的分配原则等因素.

本文首先将规划区域细分为多个小区，小区划分的原则参见相关文献［5］.假定每一小区的泊位需求量集中于小区内的一点，该点为小区内停车需求量最大的点，假定各个小区的路内停车设施需求点的坐标及其需求量是已知的.从区域路网中筛选出可以设置路内停车带的路段，则将路内停车设施布局规划选址问题转化为在平面内进行路内停车设施位置和数量分配的优化问题.路内停车场布局选址考虑的因素主要有:路内停车场与城市布局及路外停车场的协调性，泊车者从停车场到出行目的地的距离、停车的难易程度、对于闲置公共空间资源的有效利用以及停车场的投资效益等.

2 模型构建

2.1 目标函数

将规划区域划分为n个小区，则该区域内共有n个停车需求点，将第i个停车需求点的坐标表示为(xi，yi);该区域内拟建的第j个路内停车场坐标表示为表示泊车者的步行距离;sij表示由第i个需求点到第j个路内停车场的停车数量;pj为第j个路内停车场能提供的泊位数量;Bj为第j个停车场规划位置的土地单位造价;λk为第k类停车场建造型式每泊位占用的土地面积系数;Ek为第k类停车场建造型式的泊位单位造价.

决策变量为sij，即由第i个需求点到第j个路内停车场的停车数量.

目标函数分为三个部分，分别为泊车者的步行距离，规划区域内的路内停车泊位总量，路内停车泊位的建设费用.

(2)路内停车泊位总量:

(3)路内停车泊位的建设费用:

考虑到这三者之间物理量纲的不同，为其加上参数.优化的目标函数为:

G=M+μ·L－ν·N，其中

2.2 约束条件

(1)路内停车场泊位供应总量约束

规划区域内设置的路内泊位数量应不小于规划部门给出的泊位总量的最低满意值.即为规划部门给出的泊位总量的最低满意值;

(2)每个路内停车场泊位供应量约束

考虑到道路的等级、长度、交通流运行状况等因素的影响，每一个路内停车带能提供的泊位数量应限定在一定的范围之内.即pmin≤pj≤pmax，pmin，pmax分别为每一备选停车场可以提供的泊位数的下、上限;

(3)步行距离约束

停车者到达目的地的步行距离应在可接受的上限值之内.即lij≤R，R为停车者步行至目的地可接受的步行距离上限;

(4)路内停车需求数量约束

每个路内停车需求点的需求量约束.即Sij≥0，Sij为第i个停车需求点到第j个路内停车场的停车数量;

(5)总投资额约束

2.3 数学模型

根据上述分析，建立考虑步行距离、建设费用、泊位总量等多个目标和投资额、停车需求、步行距离等约束条件的数学模型，具体形式如下.

G=M+μ·L－ν·N，其中

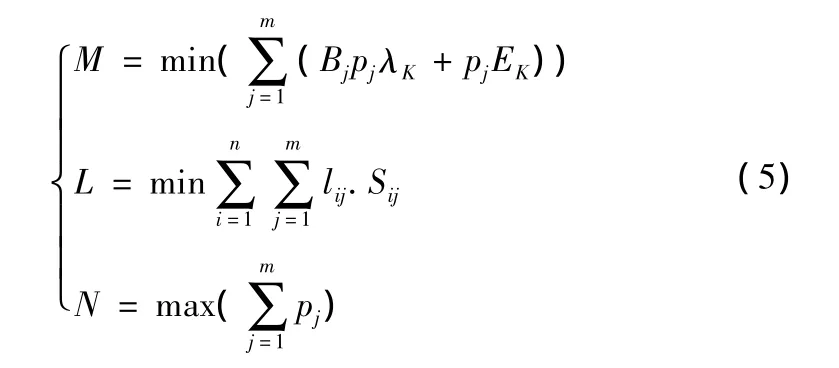
上式中:G:广义费用总和;μ，ν:因物理量纲不同而引入的参数;(xi，yi):各小区需求点的已知坐标各路内停车场的坐标，j=1，2，…，m;aij:第j个停车需求点可由第i个路内停车场服务的测度;R:停车者步行至目的地可接受的步行距离上限;其余符号含义同上.

3 模型的求解算法

3.1 模型的求解过程

本文中模型的求解分为两个阶段:首先是按一定的原则将规划区域划分为多个小区，根据相关路内停车泊位设置规范，从规划区域路段中筛选出可以建设路内泊位的路段集合s1，则路内停车备选点所在的道路及备选点的坐标值变为已知;对于划分好的每一个区域，其路内停车泊位的需求点坐标及其需求量是已知的.第二阶段是运用本文提出的模型从筛选出的备选集合s1中确定出问题的非劣解集，确定每一功能小区内路内泊位的设置点及其数量分布情况.

模型中包含了多个目标，使用常规优化算法的计算量较大，为提高效率，本文引入遗传算法来对模型进行计算，以减小计算量.利用遗传算法的的全局处理能力和隐含并行性可以提高算法寻优的能力，保证以较大概率找到最优解.

3.2 模型的求解步骤

步骤1:数据准备.首先根据所选区域的道路网特性及周围土地利用性质，对研究区域进行划分，建立相应的坐标系，将研究区域在平面坐标内表示出来.

步骤2:确定备选解集.对研究区域路网进行现场勘查，按照道路和交通条件得到研究区域内道路网中可以设置路内停车位的路段集合s1，并按照服务范围进行划分，得到路内停车备选点所在的道路及备选点的坐标值.

步骤3:对每一个可行的位置方案按照优化目标进行优化.建立平面坐标系，在坐标系中标出各个停车备选点的坐标和停车需求点坐标，将路内停车布局选址问题转化为在一个平面内进行停车位数量分配与位置选取的优化问题.并确定选择集内每个路内停车位布置点的坐标，从而建立模型的路内停车设施备选点坐标集合

步骤4:筛选备选点.运用Matlab遗传算法工具箱编程求解多目标规划问题，从备选点集合中筛选出非劣解，从而确定路内泊位布设的坐标及其泊位数量.

4 模型的运用

以某城市为例，假设该城市某一区域路网如图1所示.已知该区域路内泊位的需求量为300个标准泊位，分布于整个规划区域之内，各个路内泊位需求点的坐标及泊位需求量是已知的.假定停车者步行至目的地可接受的步行距离上限R为200米，区域内路网的等级属性数据见表1.

图1 某区域路内停车需求点和备选点坐标图

按照上述过程求解，首先将规划区域划分为7个功能小区，具体如图1所示.按照设置路内停车带的一般道路条件和交通条件，在图中选取设置路内停车设施的备选点.假设每一个小区的路内泊位需求集中于小区内一点，每一区域内有多条路段可作为路内泊位设置的备选路段.规划区域内各个停车需求点的坐标及其泊位需求量及路内停车备选点所在道路及其坐标值如表1所示:

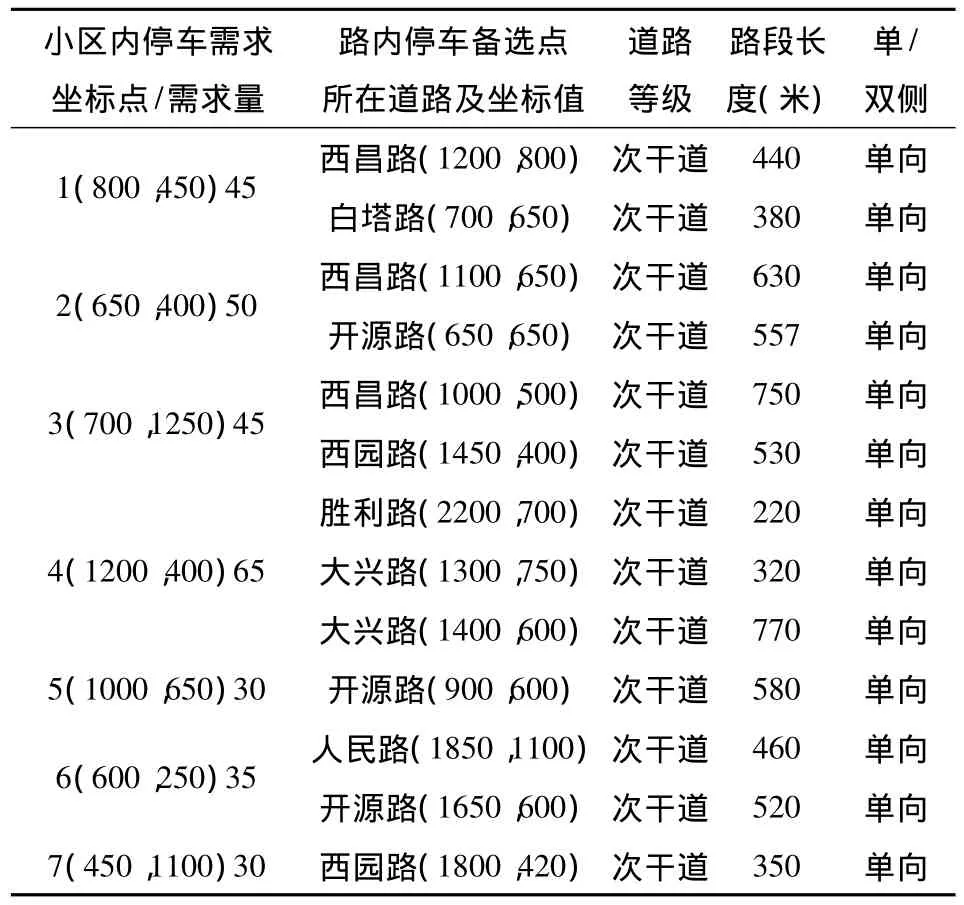
表1 某区域停车需求点坐标和路内停车设施备选点坐标

将表1中路内停车带备选点坐标、各小区内路内泊位需求点坐标代入选址模型，比较步行距离、泊位建设总费用、泊位供应量等各个指标，运用所提出的方法进行计算.可得到路内停车带布设的非劣解集，即在该区域路网内设置路内停车带的最优备选点和泊位数如表2所示.

从表2的求解结果可以看出，整个区域内共得到7个路内停车带，所提供的路内停车泊位总数为350个，每一个功能小区的路内停车需求都得到了满足，在保证区域内路内停车供给充分的前提下，泊位供应还有一定的富余，证明该布局方案是相对合理的.

表2 规划区域内路内停车最优备选点坐标及泊位数

5 结语

本文通过对影响路内停车泊位供给与需求的因素进行分析，提出了一个路内停车泊位选址优化模型，并运用遗传算法进行求解，可以得出研究区域内路内泊位设置的最佳位置与泊位数量.算例结果显示，运用该方法得到的路内泊位能够最大限度满足区域内的路内停车需求、显著提升区域内的停车服务水平，并保证泊位建设费用最小.本文提出的方法可对路内停车带选址研究提供参考.

［1］葛兴，姜波，王殿海，等.路内停车对交通流的延误影响模型［J］.城市交通，2009，(2):28 －32.

［2］梅振宇，陈峻，王炜.城市路内停车设置规模非线性优化模型及其算法［J］.交通运输工程学报，2007，(2):89 －93.

［3］王妹春，陈峻，张辉.与路外停车场协调的城市路内停车设施选址优化模型［J］.公路交通科技，2009，(5):97－102.

［4］梁军，李旭宏，于洪君，等.路边停车对路段交通流的影响研究［J］.公路交通科技，2003，(2):85 －95.

［5］梅振宇.城市路内停车设施设置优化方法研究［D］.南京:东南大学博士学位论文，2006.