基于区间需求下系统总时间最小的混合交通网络设计优化模型*

杨 鹏，杨阳梅

(长沙理工大学交通运输工程学院，湖南长沙410076)

交通网络设计问题(NDP)是交通科学研究的热点问题之一.NDP问题通常分为连续交通网络设计问题(CNDP)和离散交通网络设计问题(DNDP)两种，前者针对改扩建，后者针对新建道路，而在实际交通网络设计中，这两种情况往往同时存在，称之为混合交通网络设计问题(MNDP).

1973年Morlok首次提出交通网络设计问题，近30年来国内外学者在交通网设计模型和算法研究中取得很多成果，并在实际应用中取得不错成效.Ben－Ayed［1］给出交通网络设计双层规划模型的一般公式.孙华等［2］考虑交通发生、吸引量是确定的，而OD需求是不确定情况下连续交通网络设计问题，提出了利用鲁棒优化方法建立用户均衡约束下的极大极小模型.陆化普等［3］假定OD需求是满足给定概率分布的随机变量，采用随机抽样的方式形成需求情景集合，建立了OD需求不确定的离散交通网络设计双层规划模型.周和平［4，5］研究混合网络设计模型时，将连续交通网络设计转化为离散交通网络设计问题，建立混合交通网络设计模型.

目前，传统的“四阶段法”忽视需求的不确定性，虽有学者提出不确定的来源有:内在不确定性、输入不确定性以及传播不确定性，但预测模型产生的结果却是唯一的，这样的预测结果具有很大的风险性.自Moore提出区间分析以来，由于区间数在度量交通需求不确定的特殊优势，带区间参数的多属性决策优化方法成为研究的热点.Martorell［6］提出一种解决区间约束的遗传算法.Averbakh对带区间数的后悔网络优化问题进行了研究.Kasperski［7］对带区间数的 Minmax后悔优化问题进行了研究，并提出一种近似算法.Kasperski在其专著中，采用最小最大后悔值模型，对带区间数的离散优化问题进行研究，给出了最短路、最小割集、指派问题等经典问题的求解算法.徐泽水等［8］提出基于可能度的区间数排序法，该方法具有较强的实用性，故本文涉及的区间数排序采用此方法.区间数排序公式如下:

前文已经论述了交通网络设计问题分为离散型交通网络设计和连续型交通网络设计问题，将连续交通网络问题转化为离散交通网络设计问题;周和平提出一种方法，可同时得到公路的等级与车道数.根据《公路工程标准》，公路分为5个等级，车道数可分为2，4，6，8，12等，将公路等级和车道数进行组合编号，并以此作为决策变量，如表1所示.

表1 决策变量及其对应值

1 模型建立

给定交通网络G=(N，C)，定义N为网络节点的集合，C为网络边的集合，其中，A为改造路段的集合，B为新建路段的集合;R和S为网络中起点和讫点的集合为路段交通量，包括改造和新建路段交通量，组成向量xa为改造路段决策变量，xb为新建路段决策变量;H为路段总投资概算.

本文运用双层规划模型，上层为区间需求下系统总时间最小值模型，下层为区间需求下交通分配用户均衡模型.

1.1 目标函数

以系统总时间最小值为目标，建立优化模型，即:

1.2 约束条件

1.2.1 投资约束

公路网络建设耗资巨大，一旦网络设计不当，将造成无法挽回的损失，故将整个网络的投资预算作为约束条件，即:

其中:la为已有路段a的长度，lb为新建路段的长度;ca(xa)为已有路段a的投资函数;cb(xb)为新建路段b的投资函数;H为整个网络的投资总额.

1.2.2 可行域约束

给决策变量一个可行范围，可以有效减小搜索空间，提高搜索效率.首先确定整个路网的邻接关系，剔除不能连接的边，建立备选路段.

对于已有路段，假定改造后路段的服务能力不能低于现有路段的服务能力，即:

对于新建路段，决策变量在规定的范围内取值即可:

1.3 数学模型

上层混合交通网络设计模型［MNDP］

下层基于区间需求交通分配用户均衡模型［IUE］

2 算法设计

双层规划模型是NP完全问题，用传统方法很难求解，本文采用基于区间分析的遗传算法求解以上模型.本文编码采用实数编码，编码包括改造方案和新建方案.遗传算子选择采用轮盘赌选择、交叉采用两点交叉、变异采用基本位突变.

计算步骤如下:

步骤1:根据实际网络状况，生成可能的初始交通网络图，生产备选方案集，包括新建的路段集A和需要改进的路段集B;

步骤2:设定种群规模Np、交叉概率pc、变异概率pm和最大迭代次数Nh的值.根据交通网络图的可能连接关系随机生产生成一个种群并设置初始进化代数gen=0;

步骤3:转入下层进行交通流量分配，将路段交通量和走行时间的计算结果返回上层;

步骤4:计算各个个体对应的目标函数和适应度函数值，同时验证各个个体是否满足约束条件，对不满足的个体加以惩罚值;

步骤5:如果迭代次数gen≻Nh，转Step 10，否则Gen=Gen+1，转入下一步;

步骤6:进行选择、交叉、变异操作;

步骤7:算法终止，输出结果.

3 算例分析

采用图1的交通网络图验证模型和算法的可行性，该网络包含有9个节点，14条路段，其中1～12号路段为改造路段，用实线表示，13～16号路段为新建路段，用虚线表示(见图1).

图1 交通网络图

表2和表3分别为OD需求矩阵和各路段相关参数.

表2 OD流量矩阵

表3 路段相关参数

本文采用Matlab的区间分析工具箱和遗传算法工具箱实现.编码采用1－5的实数编码，染色体长度为16位，前12位为改造路段，后4位为新建路段，根据道路编号排列;种群规模为30，进化代数200次，交叉概率为0.85，变异概率为0.03，投资限额为400亿元.计算结果为:

图2 区间数种群进化示意图

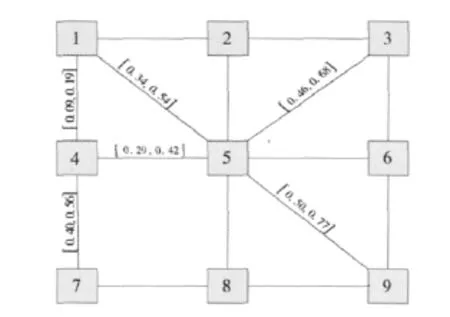
图3 区间数方案路段服务水平示意图

图3是种群进化示意图，算法在22代得到最优解，适应度函数值为5.2 ×104，对应的染色体编码为［4，5，5，3，3，5，2，5，5，3，3，2，5，4，0，1］，其中改造路段编号为:1，2，3，6，8，9，10，11;新建路段为:13，14，16;方案总投资为356.24亿元.图3 是方案路段服务水平，可以看出方案各路段交通状况良好.

4 结论

本文研究了需求不确定条件下，建立基于系统总时间最小的混合交通网络设计优化模型，将区间分析和遗传算法相结合，设计求解算法.该模型能够避免交通网陷入Braess诡异，同时考虑交通需求的不确定性，具有很强的应用价值.

［1］Ben－Ayed O，Boyce D E，Blair C E.A general bilevel linear programming formulation of the network design problem［J］.Transportation Research Part B:Methodological，1988，(22):311 －318.

［2］孙华，高自友，龙建成.不确定OD需求下连续交通网络设计的鲁棒优化模型［J］.交通运输系统工程与信息，2011，(2):70－76.

［3］陆化普，蔚欣欣，卞长志.OD需求不确定的离散交通网络设计模型研究［J］.公路交通科技，2011，(5):128－132.

［4］周和平，胡列格，裴武.基于优先与公平的城市群一体化混合公路交通网络设计模型［J］.系统工程，2007，(7):92－95.

［5］周和平，晏克非，徐汝华，等.基于遗传算法的公路网络设计的双层优化模型［J］.同济大学学报(自然科学版)，2005，(7):920－925.

［6］Martorell S，Carlos S，Sánchez A，et al.Constrained optimization of test intervals using a steady－state genetic algorithm［J］.Reliability Engineering＆ System Safety，2000，(3):215－232.

［7］Kasperski A，Zieliński P.An approximation algorithm for interval data minmax regret combinatorial optimization problems［J］.Information Processing Letters，2006，(5):177 －180.

［8］徐泽水，达庆利.区间数排序的可能度法及其应用［J］.系统工程学报，2003，(1):67 －70.