基于自适应神经网络的调频调幅信号预测*

曾 英

(湖南城市学院通信与电子工程学院，湖南益阳413000)

线性调频(Chirp)信号是指频率随时间而线性改变(增加或减少)的信号，它是研究最早而且应用最广泛的一种脉冲压缩信号［1］，它的主要优点是所用的匹配滤波器对回波的多普勒频移不敏感，即使回波信号有较大的多普勒频移，仍能用同一个匹配滤波器完成脉冲压缩，这将大大简化信号处理系统.它的主要缺点是存在距离和多普勒平移的耦合.此外，线性调频信号的匹配滤波器的输出旁瓣电平较高，通常采用对SAW匹配滤波器进行加权的方法来降低压缩脉冲时间旁瓣电平.为了能够测量长距离又保留时间的分辨率，雷达需要短时间的脉冲波以及持续的发射信号.线性调频可以同时保留连续信号和脉冲的特性，因此被应用在雷达和声纳探测上［2］.本文主要利用神经网络对线性调频信号的预测进行一些研究.

1 自适应神经网络

图1是一自适应线性神经网络的结构图，图中p1，p2，p3，……pr是 r个输入，w1，w2，w3，……wr是 r个输入所对应的权值，b为偏差，根据网络结构，可以写出第i个输出神经元节点的加权输入和，网络输出 a=f(ni)［3］.

图1 自适应线性神经网络的结构图

单神经元自适应控制的结构如图2所示.

单神经元自适应控制器是通过对加权系数的调整来实现自适应、自组织功能，控制算法为

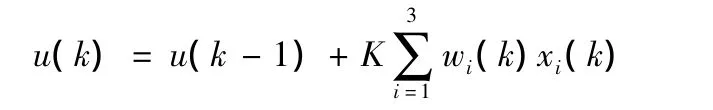
图2 单神经元自适应控制结构图

如果权系数的调整按有监督的Hebb学习规则实现［4］，即在学习算法中加入监督项z(k)，则神经网络权值学习算法为:

式中，z(k)=e(k);x1(k)=e(k);x2(k)=e(k)－e(k－1);x3(k)=Δ2e(k)=e(k)－2e(k－1)+e(k－2);η为学习速率;k为神经元的比例系数，k＞0.

2 神经网络预测控制模型的构建

预测控制是一种基于模型的控制，它是20世纪70年代发展起来的一种新的控制算法，具有预测模型、滚动优化和反馈校正等特点.已经证明该控制方法对于非线性系统能够产生有希望的稳定性.利用自适应线性神经网络可设计调频信号预测控制器.图3给出了一种神经网络预测控制的结构［5］.

图中，NNM为神经网络对象响应预报器，NNC为神经网络控制器.NNM提供的预测数据送入优化程序，使性能目标函数在选择合适的控制信号u的条件下达最小值，即

其中n为预测时域长度，m为控制时域长度，λ是控制加权因子;u(t)为控制信号;yr为期望响应，ym为网络模型响应.

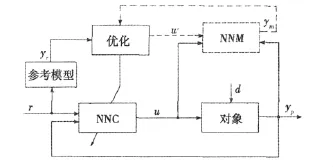
图3 神经网络预测控制系统

3 对调频信号的预测仿真及结果分析

假定有一线性调频信号f(t)=f0+kt，其中f0表示时间等于零时的频率，k表示频率改变的速率，文中设f0=0，k=160，信号采样时间为2s，采样频率为1000Hz，在Matlab里仿真得图4和图5，图4中用“——”表示输入的线性调频信号，“.”表示预测模型，图5是两信号的误差曲线图.从图中的误差曲线可以看出，在预测的初始阶段，误差较大，但经过一段时间(5个信号)后，误差几乎趋于零，这是因为在初始阶段，网络的输入需要5个延时信号，输入不完整，因此不可避免地出现初始误差.

图4 信号预测波形图

图5 误差曲线图

4 结语

论文在介绍自适应神经网络的基础上，构建了适应神经网络预测控制模型，对线性调频信号进行了预测控制，从误差曲线可以看出，在预测的初始阶段，尽管误差较大，但经过一段时间(5个信号)后，误差几乎趋于零，这是因为在初始阶段，网络的输入需要5个延时信号，输入不完整，因此不可避免地出现初始误差.如何在预测的初始阶段，减少误差，将是下一阶段继续研究的问题.

［1］范怀玉.基于自适应神经网络的信号处理［D］.郑州:郑州大学硕士学位论文，2007.

［2］Li J，Xiao W，Zhang X，et al.Denoising of power quality disturbance based on self－ adapting neural fuzzy control［J］.Information Technology Journal，2012，(11):1632 －1637.

［3］樊生文，李正熙.基于自适应滤波算法的整流器电流预测控制［J］.电气传动，2012，(1):31 －34.

［4］李加升，杨金辉，肖卫初.基于神经网络内模的岸电电源波形控制［J］.高电压技术，2012，(11):3033－3040.

［5］王海军，乔烨.基于GA－RBF模型的无线电波信号预测研究［J］.微型电脑应用，2011，(12):13 －14，69.