深部软岩巷道耦合支护方案的数值模拟

高 林 徐国强 李国峰

(1.河北联合大学建筑工程学院;2.中铁六局集团有限公司)

由于经济发展对资源需求的增加，矿产开采深度不断增加，随之引发巷道围岩大变形等一系列严重的次生工程灾害，对深部资源的安全开采提出了严峻考验［1-4］。深部围岩处于软岩状态，其工程岩体力学性质主要表现为非线性大变形力学特性，对于处于深部软岩环境下的开采巷道，其支护难度异常困难，支护方案的可行性异常重要［5-8］。本研究为了详细了解处于深部软岩环境中某运顺巷道开挖后的应力、应变分布情况，验证初步拟定的支护形方案的可靠性和支护效果，根据对该运输顺槽的变形破坏特征的分析，选取了变形较大的开口位置为研究对象，依据巷道赋存地质情况及巷道实际形状、大小，对采用“锚网+钢带+锚索+喷射混凝土支护”(方案一)和“恒阻大变形锚杆+钢带+底角注浆锚管支护”(方案二)2种耦合支护方案，利用大型的有限差分软件FLAC3D来进行开挖后的动态模拟。

1 计算模型的建立

利用MIDAS/GTS完成巷道几何模型、地质界面的生成，随后进行网格划分并保存单元和节点的几何信息，FLAC3D的前处理数据格式通过EXCEL处理后转化而成，并应用Import Grid命令将前处理数据导入，从而生成地质力学模型和支护工况模型如图1、图2所示，计算所采用的物理力学参数见表1。

表1 支护物理力学参数取值

图1 方案一模型

图2 方案二地质力学与支护工况模型

2种支护方案的模型均由四面体单元构成，计算范围为长×宽×高=20 m×40 m×40 m。支护方案一共划分63 502个单元，11 954个节点;支护方案二共划分25 370个单元，5 051个节点。模型限定条件为侧面水平固定，底部固定，模型上表面为应力边界，并采用13.5 MPa的荷载模拟上覆岩体的自重边界。分别采用SHELL单元、cable单元和pile单元模拟混凝土喷层、恒阻锚杆和底角锚管的抗弯特性。材料破坏符合Mohr－Coulomb强度准则。巷道为穿越甲2煤层、泥岩和凝灰岩的穿层巷道。

2 支护方案模拟计算结果对比分析

2.1 位移场分布规律分析

巷道位移场分布如图3、图4所示。

图3 支护方案垂直方向位移场分布

从图3和图4来看，支护方案一的围岩变形较大，其中最大顶板下沉量达到692 mm，最大底鼓量达到634 mm，左帮移近量达到625 mm，右帮移近量达到541 mm，两帮移近量共计达到1 166 mm，超过合理变形范围，且左帮变形明显大于右帮;支护方案二的围岩变形比较均匀且变形较小，最大顶板下沉量为215 mm，最大底鼓量为204 mm，左帮移近量为175 mm，右帮移近量为180 mm，两帮移近量共计355 mm，在合理变形范围内。

支护方案一中，由于“锚网+钢带+锚索+喷射混凝土”未能与围岩形成良好的耦合作用，在高应力的作用下，围岩位移变形处于不稳定状态，且底板没有支护，底板首先发生变形，当底板位移发展到一定程度，巷道顶板和两帮发生位移，最终导致大面积的顶板下沉、底鼓、帮缩、溃帮;而且巷道围岩出现整体收缩变形，且顶板和底板的总体收缩量接近于左帮和右帮的总体收缩量，属于典型的非对称大变形破坏。

支护方案二中，在“恒阻大变形锚杆+钢带+菱形网+底角锚管”的共同协调作用下，允许巷道适量变形，释放部分变性能，但支护强度始终不变。同时考虑到巷道皮带侧施工较为不便，在皮带侧打入2根锚管，比非皮带侧少1根锚管，因此使底板出现非对称变形，但整体底板位移量较小。依据模拟结果分析可知，底脚锚管注浆填充了底板围岩内的裂隙，加强了底板的强度，强化了底板整体性，阻断了塑性滑移线的发展，限制了底板的移动，可以有效防止底板发生较大底鼓。

2.2 应力场分布规律分析

应力场分布如图5～图7所示。

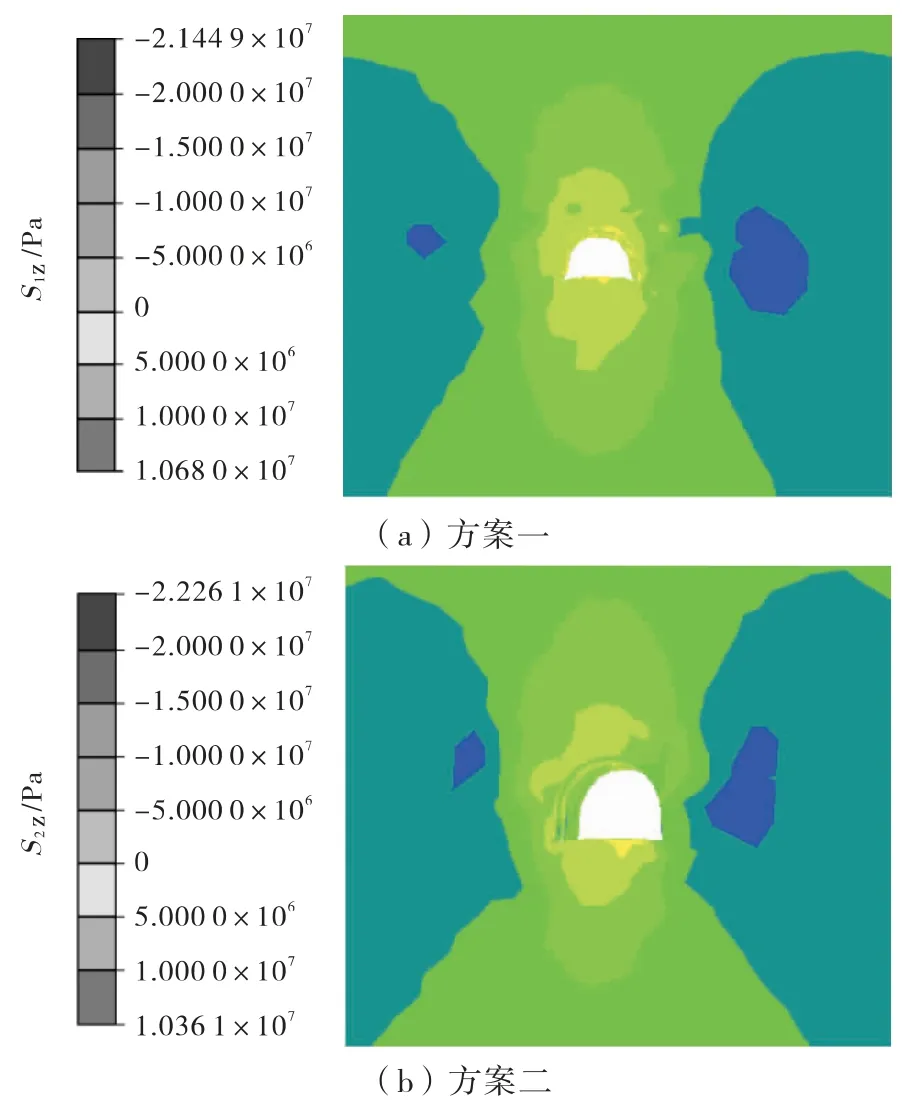
图5 支护方案垂直方向应力场分布

图6 支护方案水平方向应力场分布

图7 支护方案剪应力场分布

从图5～图7可见，支护方案一的巷道两帮形成垂直应力集中区，垂直应力集中达到2.14×107N/m，巷道底板和顶板形成水平应力集中区，水平应力集中达到1.55×107N/m，在2个帮角和顶板两侧深处形成剪应力集中区，剪应力集中分别达到5.49×106N/m和5.18×106N/m;支护方案二的巷道两帮形成垂直应力集中区，垂直应力集中达到2.23×107N/m，其水平应力和剪应力分布相对较为均匀，仅在个别点位出现与支护方案一的水平应力和剪应力值相近的应力集中点。相比较而言，支护方案二对于巷道围岩应力分布的控制比较理想。

支护方案一中，由于两帮和顶板的支护强度不足，无法有效控制巷道底板的变形，减少巷道的底鼓量，巷道两帮出现的应力集中，易导致巷道溃帮现象的发生;支护方案二中，由于底角锚管的打入，有效切断了水平应力向底板的传递，底板水平应力分布较为均匀，说明底角锚管对于控制底鼓的作用是十分明显的。

2.3 破坏场规律分析

巷道塑性区分布特征如图8所示。

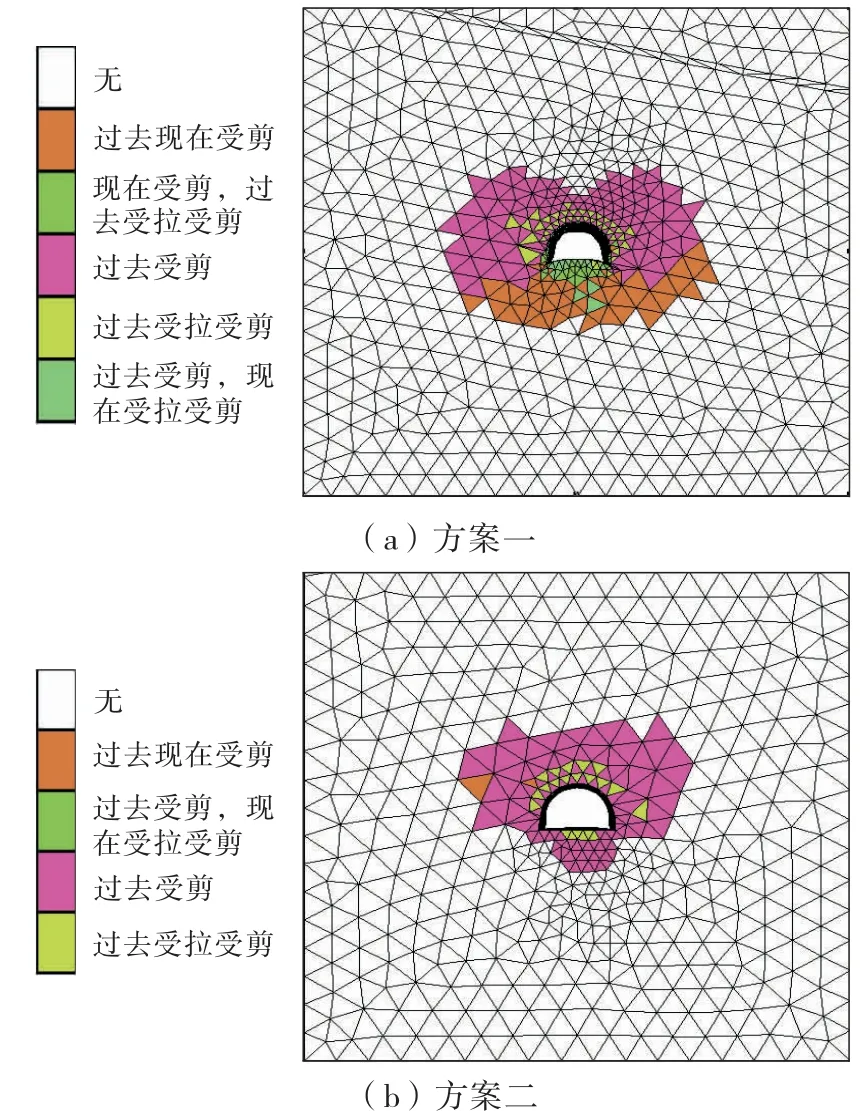
图8 支护方案塑性区分布

从图8可以看出:巷道的破坏是一个复杂的变形过程，巷道开挖后围岩应力状态重新分布，塑性区进而得以发展。支护方案一的塑性区分布范围相对较大，最大扩展范围为6 m，且该区域范围内的围岩基本处于塑性状态，巷道的整体稳定性能无法保证。支护方案二的塑性区分布范围相对较小，基本分布于巷道周边2 m的范围，仅部分围岩进入塑性状态。由此可以看出，支护方案二对于巷道围岩的变形控制是十分有效的。在支护方案一中采用锚网、锚索支护后，没有实现预期的支护体与围岩的耦合作用，无法有效限制支护范围内的围岩变形;当围岩变形发展到一定程度，破坏也由围岩表层逐步向围岩深部扩展;破坏的深入又引发了围岩的更大程度变形和破坏，并逐步超出了支护体的支护能力，使得支护体无法约束和控制围岩变形，最终导致支护体发生破坏。在支护方案二中采用恒阻大变形锚杆支护后，顶板及两帮的塑性区的范围有所减小，在恒阻大变形锚杆允许围岩有一定的变形的前提下，允许部分围岩进入塑性状态;底角注浆锚管控制底板后，底板塑性区的范围大面积减小。

2.4 支护体受力分析

支护体受力(最大表面位移)运算时步关系曲线如图9所示。

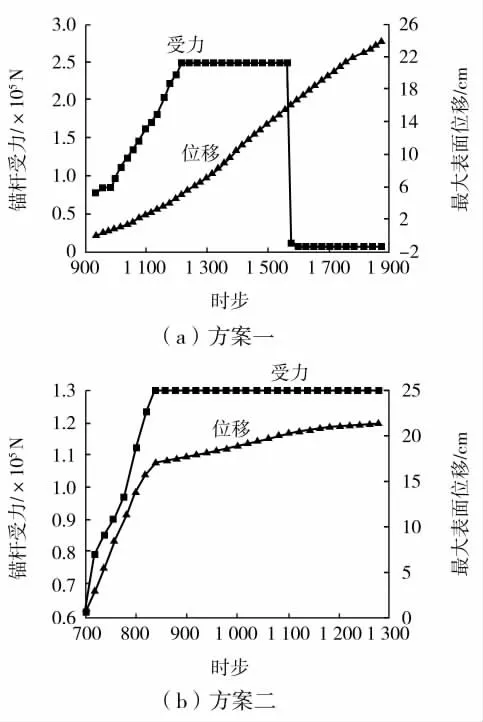
图9 支护体受力(最大表面位移)－运算时步关系曲线

可见，支护方案一中给予锚杆施加588 kN的预紧力，锚杆受力随着围岩变形的增加而逐渐增大，但锚杆受力与围岩变形趋势并不同步。当围岩变形值达到215 mm时，支护体达到设计最大抗拉强度值2 450 kN，此时围岩的变形仍在发展，由于支护体不能与围岩实现协调变形，当围岩变形到一定程度，超过锚杆自身的可延伸长度时，支护体失效，围岩变形继续发展，最终导致巷道失稳。支护方案二中给予恒阻锚杆施加588 kN的预紧力，恒阻锚杆受力随着围岩变形的增加而逐渐增大，且恒阻锚杆受力与围岩变形趋势基本同步，当恒阻锚杆达到且保持着1 274 kN的设计要求时，围岩变形值始终控制在220 mm范围内，此时恒阻锚杆在保持恒阻的同时仍能发生变形，最终达到巷道的整体稳定。

3 结论

通过对2种支护方案的数值模拟分析，可以看出，支护方案一的整体变形量较大，其中主要表现为底鼓量较大，主要因为开放性底板导致的能量从底板优先释放;支护方案二的耦合支护作用显著，通过底角注浆锚管切断应力向底板滑移的路线，能够将底鼓量控制在允许的范围内，同时通过恒阻大变形锚杆释放围岩内的部分能量，有效控制围岩变形，实现了支护体与围岩的耦合，能有效控制围岩稳定性。

［1］ 何满潮.深部开采工程岩石力学的现状及其展望［C］∥第八次全国岩石力学与工程学术大会论文集.北京:科学出版社，2004:88-94.

［2］ 钱七虎.非线性岩石力学的新进展——部岩体力学的若干问题［C］∥第八次全国岩石力学与工程学术大会论文集.北京:科学出版社，2004:10-17.

［3］ 钱七虎.深部地下工空间开发中的关键科学问题［C］∥第230次香山科学会议文集.北京:科学出版社，2004:2004.

［4］ 何满潮，谢和平，彭苏萍，等.深部开采岩体力学研究［J］.岩石力学与工程学报，2005，24(16):2803-2813.

［5］ 何满潮，李国峰，任爱武，等.深部软岩巷道立体交叉硐室群稳定性分析［J］.中国矿业大学学报，2008，37(2):167-170.

［6］ 李国峰，蔡 建，郭志彪.深部软岩巷道锚注支护技术研究与应用［J］.煤炭科学技术，2007(4):44-47.

［7］ 郭志彪，李国峰.兴安煤矿深部软岩巷道底鼓破坏机理及支护对策研究［J］.煤炭工程，2009(2):66-70.

［8］ 李国峰，李占金，唐强达.鹤煤五矿深部软岩巷道变形机理及控制对策研究［J］.煤炭工程，2010(1):60-63.