Joint probability distribution of winds and waves from wave simulation of 20 years (1989-2008) in Bohai Bay

Xiao-chen YANG, Qing-he ZHANG*

State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, P. R. China

Joint probability distribution of winds and waves from wave simulation of 20 years (1989-2008) in Bohai Bay

Xiao-chen YANG, Qing-he ZHANG*

State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, P. R. China

The joint probability distribution of wind speed and significant wave height in the Bohai Bay was investigated by comparing the Gumbel logistic model, the Gumbel-Hougaard (GH) copula function, and the Clayton copula function. Twenty years of wind data from 1989 to 2008 were collected from the European Centre for Medium-Range Weather Forecasts (ECMWF) database and the blended wind data of the Quick Scatterometer (QSCAT) satellite data set and re-analysis data from the United States National Centers for Environmental Prediction (NCEP). Several typhoons were taken into account and merged with the background wind fields from the ECMWF or QSCAT/NCEP database. The 20-year data of significant wave height were calculated with the unstructured-grid version of the third-generation wind wave model Simulating WAves Nearshore (SWAN) under extreme wind process conditions. The Gumbel distribution was used for univariate and marginal distributions. The distribution parameters were estimated with the method of L-moments. Based on the marginal distributions, the joint probability distributions, the associated return periods, and the conditional probability distributions were obtained. The GH copula function was found to be optimal according to the ordinary least squares (OLS) test. The results show that wind waves are the prevailing type of wave in the Bohai Bay.

wind speed; wave simulation; joint probability distribution; copula function; conditional probability distribution

1 Introduction

In recent years, offshore platforms have been widely used for oil and gas production in the Bohai Bay. Traditionally, univariate distributions are used to obtain design wind parameters and wave parameters with different return periods for the structures. However, as winds and waves are actually non-independent, bivariate joint probability distribution and conditional distribution may be more realistic.

In ocean and coastal engineering, bivariate joint probability distributions of waves and winds have been investigated through the Poisson-mixed Gumbel distribution (Liu et al. 2002; Dong et al. 2003), Gumbel logistic model (Zhou and Duan 2003), Poisson bivariate logisticdistribution (Dong et al. 2005), and bivariate Pearson type III distribution (Dong et al. 2006). However, the marginal distributions are usually restricted to a certain type. Researchers have therefore introduced the copula function (Joe 1997; Nelsen 2006), which is capable of linking arbitrary marginal distributions to the joint probability distribution. As an efficient tool, the copula function has been applied widely in the financial sector, and recently in hydrology (De Michele and Salvadori 2003; Favre et al. 2004; Salvadori and De Michele 2004a, 2004b, 2006; De Michele et al. 2005; Grimaldi and Serinaldi 2006; Niu et al. 2009), whereas only a few studies on the copula-based joint probability distribution have been carried out for coastal and ocean engineering (Nerzic and Prevosto 2000; Wist et al. 2004; De Michele et al. 2007; Qin et al. 2007; Dong et al. 2011; Chen 2011). For the copula-based joint probability distribution analysis of extreme wave height and wind speed, Gumbel-Hougaard (GH) and Clayton copulas of the Archimedean copula family have been most commonly used. Qin et al. (2007) analyzed the wind-wave joint probability distribution in the South China Sea using the Clayton copula function. Dong et al. (2011) introduced the bivariate Gumbel Clayton copula distribution based on the Clayton copula function. Chen (2011) used bivariate copula functions to analyze the joint probability distribution of extreme wave height and wind speed in the Shanwei sea area. Several copula functions were compared and the GH copula function was found to be the optimal selection through goodness-of-fit tests. In general, the optimal distribution was related to the samples. Therefore, the objective of this study was to use the common distributions, such as the Gumbel logistic model, the GH copula function, and the Clayton copula function, to investigate the bivariate joint probability distribution and extreme values with certain return periods for winds and waves in the Bohai Bay.

In order to investigate the joint probability distribution of winds and waves in the Bohai Bay, continuous wind and wave data for at least 20 years are required to calculate the probability distributions of extreme winds and waves. However, the measurements of sea surface wind over the Bohai Sea are too sparse to provide a wind field for this study. As a result, the wind data were obtained from the QSCAT/NCEP blended ocean wind data set (http://dss.ucar.edu/datasets/ds744.4/) and the ECMWF 40-year re-analysis data set (http://data portal.ecmwf.int/data/d/era40_daily/). Due to the increasing performance of computational resources, the numerical method may provide an alternative to the observed wave data. The well-established third-generation wind wave model Simulating WAves Nearshore (SWAN) (Booij et al. 1999) has played an important role in wind wave numerical modeling, and in recent years the model has been widely applied in the Yellow-Bohai Sea (Wang et al. 2004; Li and Bo 2005; Deng et al. 2007; Zheng et al. 2010). Recently, Zijlema (2010) proposed an unstructured mesh for SWAN, which can describe the complex coastal boundaries and offer a good alternative to the traditional structured-grid nested model. In this study, numerical simulation of wave processes during extreme wind processes in each year was carried out using the unstructured-grid version of the SWAN model for a 20-year duration from 1989 to 2008.

2 Joint probability distribution models

2.1 Gumbel logistic model

The Gumbel logistic model has been used in the fields of ocean engineering (Zhou and Duan 2003) and hydrology (Yue 2001), with the Gumbel distribution as the marginal distribution. It is expressed as follows:

whereF(x) andF(y) are the marginal distributions of two random variablesXandY, respectively; andmrepresents the association between the two random variables, estimated as

whereρis the correlation coefficient and is expressed as

whereμXandμYare the means ofXandY, respectively, andσXandσYare the standard deviations ofXandY, respectively.

2.2 Copula function

Copula functions are not restricted to a certain type of distribution like the marginal distribution. The Gumbel-Hougaard (GH) copula and the Clayton copula have been most commonly used in coastal and ocean engineering and performed well (Qin et al. 2007; Dong et al. 2011; Chen 2011) .

The GH copula function is expressed as follows:

whereτis the Kendall’s correlation coefficient, andθis a parameter describing the dependency relationship between the two variables.

The Clayton copula function is expressed as

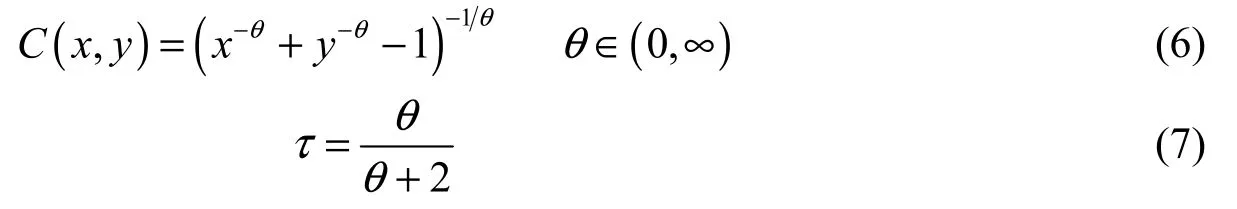
Based on the copula functions, the bivariate joint probability distribution is expressed as

2.3 Return period and conditional probability distribution

The return periods for the variablesXandYexceeding certain values are expressed,respectively, as follows:

The joint return periodT(x,y) of eitherXorYor both exceeding the corresponding valuesxandy(X＞x,Y＞y, orX＞xandY＞y) can be expressed as

The joint return periodT0(x,y) of bothXandYexceeding the corresponding valuesxandy(X＞xandY＞y) is expressed as

The conditional probability ofXx≥ given thatYy≥ is expressed as

The conditional probability of other conditions can also be calculated.

3 Application

3.1 Wind data

The extreme wind processes and annual extreme wind speeds from 1989 to 1999 were taken from the ECMWF data (from September 1957 to August 2002) and the wind data from 2000 to 2008 were taken from the QSCAT/NCEP data (from July 1999 to July 2009). The spatial resolutions of the QSCAT/NCEP and ECMWF data were 0.5° × 0.5° and 2.5° × 2.5°, respectively. The temporal resolution of both data sets was 6 h. According to the wind data time series from the Bohai Bay, extreme wind processes with greater wind speed and wind fetch length, as well as longer acting time, were selected for wave simulation.

When comparing the extreme wind speed data from QSCAT/NCEP with those from ECMWF at the same place during the same extreme wind processes, values of most extreme wind speeds from QSCAT/NCEP were larger than those from ECMWF. Since the QSCAT/NCEP surface wind data were blended with the satellite-observed data, in order to unify these two sets of data, the ECMWF wind speeds should be modified. A linear relation, with a correlation coefficient of 0.70, was found between the extreme wind speeds from QSCAT/NCEP and ECMWF during the same period. It was demonstrated that the values of the wind speed from QSCAT/NCEP were 1.79 times those from ECMWF.

Furthermore, during the entire 20 years, typhoons Ellie in 1994, Winnie in 1997, and Matsa in 2005 were taken into account because their paths were near the Bohai Bay and could probably cause extreme waves. The path, pressure, wind speed, and other information aboutthe typhoons were collected from the Zhejiang Real-Time Typhoon Data System (http://slt.zj.gov.cn/typhoneweb) and the Unisys Weather System (http://weather.unisys.com/ hurricane). The QSCAT/NCEP or ECMWF wind data, as the background wind field, were merged with the typhoon data to obtain the wind fields during typhoons.

Both the QSCAT/NCEP and ECMWF wind data sets have been employed in atmospheric analysis (Tu and Yao 2010; Zhang et al. 2011). In this study, real-time wind data from the QK18 platform in the Bohai Sea (Fig. 1) and an observation station A with a water depth of 50 m in the Yellow Sea (Fig. 1) were collected for verification. Comparison between the observations and the QSCAT/NCEP and ECMWF wind data are shown in Fig. 2. Both the QSCAT/NCEP and ECMWF wind data show reasonable agreement with the measured wind data. In addition, the observed wind data from the observation station B (with a longitude of 122.3°E and a latitude of 27.3°N) in the East Sea during typhoon Matsa in 2005 were collected to verify the wind data under the condition of typhoons. Fig. 3 shows the comparison between the observations and the wind data merged by the QSCAT/NCEP data and typhoon data at station B. It demonstrates that the accuracy of the wind data during typhoon weather is acceptable.

Fig. 1 Sketch map of Yellow-Bohai Sea and locations of observation stations and sampling point

Fig. 2 Comparison of wind speed between observations and data from different wind databases at different observation stations

Fig. 3 Comparison of wind speed between observations and wind data merged by QSCAT/NCEP data and typhoon data at station B

3.2 Wave simulation

The wind wave model SWAN, which is based on the action balance equation (Booij et al. 1999), was employed in this study. Several source and sink terms were included in the equation to take account of the processes that generate, dissipate, or redistribute wave energy. Recently, the unstructured-grid version of the SWAN model was presented by Zijlema (2010) with a vertex-based, fully implicit, finite difference method. The unstructured grid allowed for a locally refined grid and was more suitable for describing the irregular shoreline. Therefore, the unstructured-grid version of the SWAN model was used in this study.

Zijlema (2010) selected two academic test cases and one realistic wind-sea case to show the correctness and numerical accuracy of the unstructured-grid version of the SWAN model. In this study, significant wave heights collected at the BZ28 platform in the Bohai Sea (Fig. 1) and station A in the Yellow Sea (Fig. 1) were compared with the simulated results and are shown in Fig. 4. The computation domain included the Yellow-Bohai Sea areas with an open boundary at a latitude of 37°N to give the waves a fully developed process. The model grid was locally refined at the Bohai Bay area, with a minimum size of about 350 m. The bathymetry was interpolated onto the grid and is shown in Fig. 1. Waves were driven by winds,and the wind data from QSCAT/NCEP or ECMWF were used, as described in section 3.1. The time step was set at 10 min. The discrete frequency was set from 0.04 to 1.0 Hz, and the bottom friction was set at 0.01 m2/s3. The simulated significant wave heights fit well with the measured data, which further demonstrated the capability of the unstructured-grid version of the SWAN model.

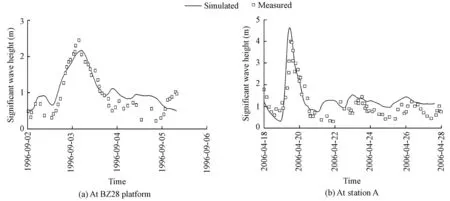
Fig. 4 Comparison of measured and simulated significant wave heights

Using selected wind processes, the entire 20-year wave fields were simulated. We selected a sampling point (Fig. 1) on a 20 m-depth contour for further analysis. From the wind data and the simulated wave data, the annual extreme wind speed and the corresponding significant wave height, and the annual extreme significant wave height and the corresponding wind speed can be obtained and used in the analysis of univariate and bivariate joint probability distributions.

3.3 Univariate analysis

The annual extreme wind speed (Vm) and annual extreme significant wave height (Hsm) were collected for univariate analysis. We used the Gumbel distribution for bothVmandHsm:

whereuxandαxare, respectively, the location and scale parameters of the Gumbel distribution and can be estimated with the method of L-moments.

The univariate distributions ofVmandHsmare shown in Fig. 5, wherePis the cumulative frequency, and the univariate design factors for different return periods are shown in Table 1.

Fig. 5 Univariate distribution of annual extreme wind speed and annual extreme significant wave height

3.4 Bivariate analysis

Two pairs of data, the annual extreme wind speed and the corresponding significant waveheight (Vm,Hs), and the annual extreme significant wave height and the corresponding wind speed (Hsm,V) were collected for bivariate analysis. The marginal distributions of wind sp eed and significant wave height were also estimated by the Gumbel distribution and are presented in Fig. 6.

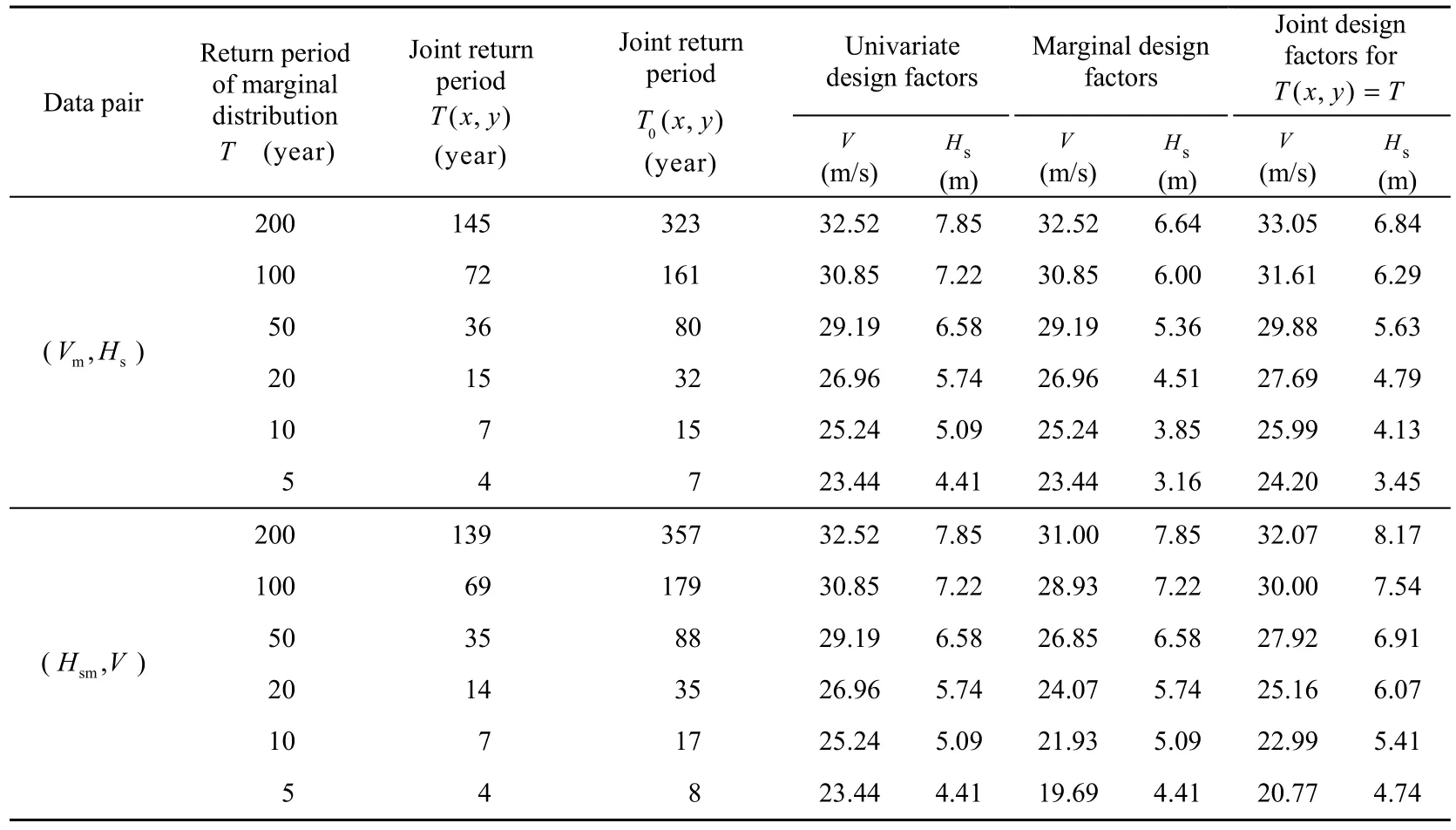
Table 1 Design values of wind speed and significant wave height for different return periods

Fig. 6 Marginal distribution of wind speed and significant wave height

The ordinary least squares (OLS) method was introduced to assess the joint probability distribution models. The OLS value (OLS) was estimated as follows:

wherePiandPeiare, respectively, the theoretical frequency and empirical frequency, andnis the sample size.

The OLS values for the Gumbel logistic model, the GH copula function, and the Clay toncopula function were 0.073, 0.065, and 0.066, respectively. The GH copula function was selected because it had the smallest OLS value.

The three-dimensional diagram of the joint cumulative distribution function (CDF) and the contours of the joint return periodT(x,y) for (Vm,Hs) are shown in Fig. 7 and Fig. 8, respectively. For each pair, assuming a same frequency ofXandY, with a given return periodT, the joint design wave height and wind speed can be obtained. Results of marginal and joint design waves and winds as well as the joint return periods for both data pairs are shown in Table 1.

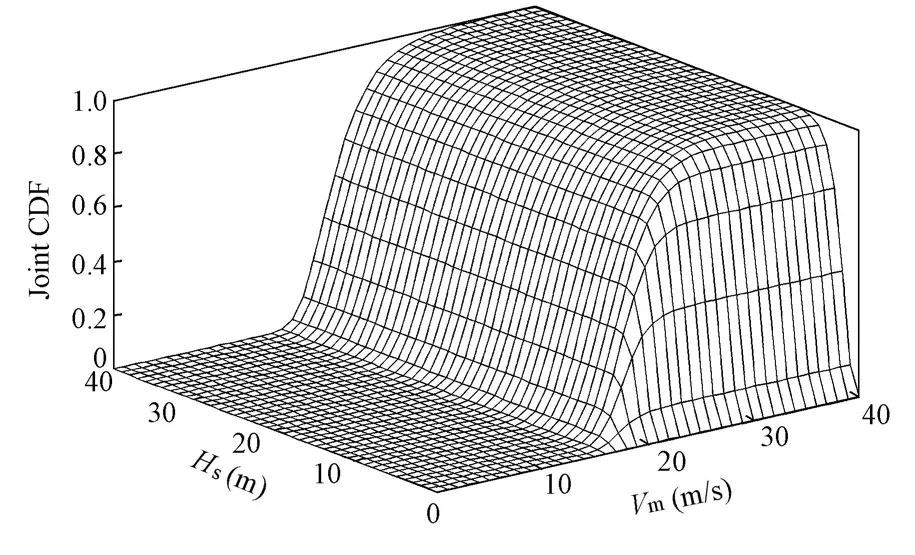
Fig. 7 Three-dimensional diagram of joint cumulative distribution function for (Vm,Hs)

Fig. 8 Joint return periodT(x,y) contours for (Vm,Hs) (Unit: year)

According to Table 1, the marginal return period is larger than the joint return periodT(x,y), but smaller thanT0(x,y). The joint design wave height and wind speed have larger values than the marginal design factors. Compared with the univariate distribution, for (Vm,Hs), the joint design wind speeds are 1.6% to 3.2% larger than the univariate design wind speeds and the joint design wave heights are 12.9% to 21.8% smaller. However, this is reversed for (Hsm,V), where the joint design wind speeds are 1.4% to 11.4% smaller and the joint design wave heights are 4.1% to 7.5% larger.

The conditional probability distribution is necessary because it provides information on the encounter probability of two conditions. From Table 2 and Table 3, for (Vm,Hs), the encounter probability of the conditions with the same frequency is larger than 62%, and for(Hsm,V), it is larger than 56%. For (Vm,Hs), the encounter probability between large design wind speed and small design wave height is very small. Also, the probability of large design wave height encountering small design wind speed is small for (Hsm,V). It is demonstrated that wind waves are prevailing in the Bohai Bay, with strong waves always encountering strong winds. This is consistent with the research of Wang et al. (2004) and Deng et al. (2007).

Table 2 Conditional probability ofVm≥xgivenHs≥yfor (Vm,Hs)

Table 3 Conditional probability ofHsm≥xgivenV≥yfor (Hsm,V)

4 Conclusions

Based on the ECMWF and QSCAT/NCEP wind data and the wave data simulated by the unstructured-grid version of the SWAN model for 20 years, a univariate distribution and a bivariate joint probability distribution were applied to the calculation of the design wind speeds and wave heights with different return periods in the Bohai Bay. The method is robust because the wind data and the simulated wave results were well matched with the measured data. The joint return periods, joint design factors, and conditional probability distribution were obtained. This study provides more information for the choice of the design factors in the Bohai Bay. The main conclusions are as follows:

(1) According to the comparison of the Gumbel logistic model, the GH copula function, and the Clayton copula function, the OLS value of the GH copula function was the smallest, which demonstrated that the GH copula function was optimal for the present samples.

(2) According to the comparison of the bivariate joint probability distribution and the marginal distribution, it can be seen that the joint return period of either wind speed or wave height or both exceeding certain values is smaller than the marginal return period, and the joint return period of both wind speed and wave height exceeding certain values is larger than the marginal return period. The joint design wave heights and wind speeds are both larger than the marginal design values.

(3) According to the comparison of the bivariate joint probability distribution and the univariate distribution, it can be seen that for data pairs of the annual extreme wind speeds and the corresponding significant wave heights, the joint design wind speeds are larger than the univariate design wind speeds and the joint design wave heights are smaller. This is reversed, however, for data pairs of the annual extreme significant wave heights and the correspondingwind speeds.

(4) The conditional probability for both data pairs shows that the encounter probability of the conditions with the same frequency is larger than 56%. The probability of small design wind speeds encountering large design wave heights is very small, and the encounter probability between small design wave heights and large design wind speeds is also small. According to the conditional distribution, wind waves are regarded to be prevailing in the Bohai Bay.

(5) Though the accuracy of wind data used in the present study was acceptable, an improvement in resolution would yield better results. Wind data calculated by an atmospheric model with better wind data sets, newly available, will be carried out in future studies.

Booij, N., Ris, R. C., and Holthuijsen, L. H. 1999. A third-generation wave model for coastal regions: 1. Model description and validation.Journal of Geophysical Research, 104(C4), 7649-7666. [doi:10.1029/ 98JC02622]

Chen, Z. S. 2011. Study on joint probability distribution of wave height and wind velocity.Marine Science Bulletin, 30(2), 158-163. (in Chinese)

De Michele, C., and Salvadori, G. 2003. A generalized Pareto intensity-duration model of storm rainfall exploiting 2-Copulas.Journal of Geophysical Research: Atmospheres, 108(D2), 4067. [doi:10.1029/ 2002JD002534]

De Michele, C., Salvadori, G., Canossi, M., Petaccia, A., and Rosso, R. 2005. Bivariate statistical approach to check adequacy of dam spillway.Journal of Hydrologic Engineering, 10(1), 50-57. [doi:10.1061/(ASCE) 1084-0699(2005)10:1(50)]

De Michele, C., Salvadori, G., Passoni, G., and Vezzoli, R. 2007. A multivariate model of sea storms using copulas.Coastal Engineering, 54(10), 734-751. [doi:10.1016/j.coastaleng.2007.05.007]

Deng, Z. Q., Zhou, L. M., Wu, L. Y., and Guo, P. F. 2007. Numerical computation of wave heights of multiyear return periods in the Bohai Sea.Transactions of Oceanology and Limnology, (s1), 8-14. (in Chinese) [doi:10.3969/j.issn.1003-6482.2007.z1.002]

Dong, S., Hao, X. L., Jiao, G. Y., and Liu, D. F. 2003. Joint probability calculation of extreme wind speed and wave height in the exploitation of marginal field.Ship Building of China, 44(s1), 247-253. (in Chinese) [doi:10.3969/j.issn.1000-4882.2003.z1.041]

Dong, S., Hao, X. L., and Fan, D. Q. 2005. Joint probability distribution of wind velocity and wave height in ocean engineering design.Acta Oceanologica Sinica, 27(3), 85-89. (in Chinese) [doi:10.3321/j.issn. 0253-4193.2005.03.012]

Dong, S., Cong, J. S., and Yu, H. J. 2006. Design parameter estimation of joint extreme significant wave height and wind speed at Weizhoudao observation station.Periodical of Ocean University of China, 36(3), 489-492. (in Chinese)

Dong, S., Zhou, C., Tao, S. S., and Xue, D. S. 2011. Bivariate Gumbel distribution based on Clayton Copula and its application in offshore platform design.Periodical of Ocean University of China, 41(10), 117-120. (in Chinese) [doi:10.3969/j.issn.1672-5174.2011.10.019]

Favre, A. C., El Adlouni, S., Perreault, L., Thiémonge, N., and Bobée, B. 2004. Multivariate hydrological frequency analysis using copulas.Water Resources Research, 40(1), 1-12. [doi:10.1029/2003WR002456]

Grimaldi, S., and Serinaldi, F. 2006. Asymmetric copula in multivariate flood frequency analysis.Advances in Water Resources, 29(8), 1155-1167. [doi:10.1016/j.advwatres.2005.09.005]

Joe, H. 1997.Multivariate Models and Multivariate Dependence Concepts. London: Chapman and Hall/CRC.

Li, Y., and Bo, Z. H. 2005. The simulation test of SWAN model in the wave height in the Yellow-Bo Sea areas.Marine Forecasts, 22(3), 75-82. (in Chinese) [doi:10.3969/j.issn.1003-0239.2005.03.013]

Liu, D. F., Wen, S. Q., and Wang, L. P. 2002. Compound bivariate extreme distribution of typhoon induced sea environments and its application.Proceedings of the 12th International Offshore and Polar Engineering Conference, 130-134. Kitakyushu: ISOPE.

Nelsen, R. B. 2006.An Introduction to Copulas.2nd ed. New York: Springer-Verlag.

Nerzic, R., and Prevosto, M. 2000. Modelling of wind and wave joint occurrence probability and persistence duration from satellite observation data.Proceedings of the 10th International Offshore and Polar Engineering Conference, 154-158. Seattle: ISOPE.

Niu, J. Y., Feng, P., and Ding, Z. H. 2009. Study of the wetness-dryness compensation characteristics of Luan river diversion reservoirs’ inflow based on multivariate Copula functions.Journal of Jilin University (Earth Science Edition), 39(6), 1095-1100. (in Chinese) [doi:10.3969/j.issn.1671-5888.2009.06.018]

Qin, Z. J., Sun, G. H., Yan, T. X., Song, H., and Zhang, J. 2007. Application of multivariate probability analysis using copulas to ocean engineering.Marine Forecasts, 24(2), 83-90. (in Chinese) [doi: 10.3969/j.issn.1003-0239.2007.02.012]

Salvadori, G., and De Michele, C. 2004a. Analytical calculation of storm volume statistics involving Pareto-like intensity-duration marginals.Geophysical Research Letters, 31, L04502. [doi:10.1029/ 2003GL018767]

Salvadori, G., and De Michele, C. 2004b. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events.Water Resources Research, 40(12). [doi:10.1029/2004WR003133]

Salvadori, G., and De Michele, C. 2006. Statistical characterization of temporal structure of storms.Advances in Water Resources, 29(6), 827-842. [doi:10.1016/j.advwatres.2005.07.013]

Tu, X. P., and Yao, R. S. 2010. Analysis on ECMWF NWP products in TC tracking forecasting.Journal of Tropical Meteorology, 26(6), 759-764. (in Chinese) [doi:10.3969/j.issn.1004-4965.2010.06.015]

Wang, D. Z., Zhang, Q. H., and Shi, Z. 2004. Modeling of wind waves in the Bohai Bay, China.Marine Science Bulletin, 23(5), 10-17. (in Chinese) [doi:10.3969/j.issn.1001-6392.2004.05.002]

Wist, H. T., Myrhaug, D., and Rue, H. 2004. Statistical properties of successive wave heights and successive wave periods.Applied Ocean Research, 26(3-4), 114-136. [doi:10.1016/j.apor.2005.01.002]

Yue, S. 2001. The Gumbel logistic model for representing a multivariate storm event.Advances in Water Resources, 24(2), 179-185. [doi:10.1016/S0309-1708(00)00039-7]

Zhang, D. T., Zheng, C. W., Shi, L. L., Liu, Z. H., and Chen, X. B. 2011. Sea surface wind field analyze from 1999 to 2009 in the China Sea by QuickSCAT/NCEP data.Marine Forecasts, 28(4), 58-64. (in Chinese) [doi:10.3969/j.issn.1003-0239.2011.04.009]

Zheng, G. D., Zhao, H. J., Xu, F. M., and Zhang, S. H. 2010. Numerical simulation of wind waves in Bohai Sea induced by “98·04” cold wave.Port and Waterway Engineering, (2), 36-39. (in Chinese) [doi: 10.3969/j.issn.1002-4972.2010.02.009]

Zhou, D. C., and Duan, Z. D. 2003. The Gumbel-logistic model for joint probability distribution of extreme-value wind speeds and effective wave heights.The Ocean Engineering, 21(2), 45-51. (in Chinese) [doi:10.3969/j.issn.1005-9865.2003.02.008]

Zijlema, M. 2010. Computation of wind-wave spectra in coastal waters with SWAN on unstructured grids.Coastal Engineering, 57(3), 267-277. [doi:10.1016/j.coastaleng.2009.10.011]

(Edited by Yun-li YU)

This work was supported by the Science Fund for Creative Research Groups of the National Natural Science Foundation of China (Grant No. 51021004) and the National High Technology Research and Development Program of China (863 Program, Grants No. 2012AA112509 and 2012AA051702).

*Corresponding author (e-mail:coastlab@163.com)

Jul. 14, 2012; accepted Oct. 12, 2012