PWM整流器直接功率控制系统的优化设计

刘晓艳，卢健康，马 艳

(西北工业大学，陕西西安710072)

0 引 言

三相电压型PWM整流器具有单位功率因数、直流电压大小可调、动态性能良好以及可实现能量的双向流动等优点，符合“绿色电能变换”潮流，也是治理谐波和“无功”污染最根本的措施之一，因此得到了广泛研究与应用［1］。

本文首先简介了三相电压型PWM整流器主电路的拓扑结构，接着介绍了其DPC系统构成;然后在文献［1］所述DPC系统的基础上，改进了电压外环结构—— 将惯性滤波环节从前向通道移到了反馈回路中，与文献［1］原来的滤波环节设计相比，加快了系统的跟随性指标。另外，为了提高系统的稳定性和动态性能，本文将原来电压环的PI调节器改为PID调节器，再利用最平幅频法［6］设计该电压调节器的PID参数，使得系统动态性能得到优化，也实现了单位功率因数控制(动态过程结束后无功功率稳定在零值附近)。MATLAB/Simulink仿真验证结果表明，DPC系统的优化设计方案可行并且能使DPC系统性能更好。

1 三相电压型PWM整流器直接功率控制系统简介

1.1 三相电压型PWM整流器的主电路结构与数学模型

三相电压型PWM整流器(VSR)主电路拓扑结构如图1所示。图中uj(j=a、b、c)为电源相电压;ij(j=a、b、c)为三相线电流;Sj(j=a、b、c)为整流桥的开关函数;udc为直流电压;L为滤波电抗器的电感;R为交流侧滤波电抗器的等效电阻和功率管的开关损耗等效电阻之和;C为直流侧电容;RL为负载电阻［2］。

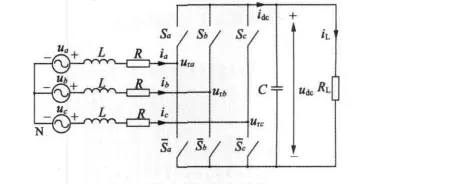
图1 三相电压型PWM整流器主电路拓扑结构图

假定三相交流电压对称，则由图1可得三相静止坐标系下的三相电压型PWM整流器的数学模型。

定义Sj(j=a、b、c)为单极性二值逻辑开关函数，其中:

1.2 三相电压型PWM整流器系统结构及工作原理

三相电压型PWM整流器主要由主电路和控制电路组成，主电路结构如图1所示。整个系统结构如图2所示。控制电路采用直流电压外环和功率内环构成双闭环结构。根据瞬时功率理论，可以在线实时计算出期望的系统瞬时有功功率和无功功率(期望的系统瞬时无功功率值为零)，然后与根据交流电压与交流电流实时计算的实际有功功率和无功功率进行比较，将比较的结果送入滞环比较器中，最后依据交流电压矢量所在的扇区与功率滞环比较器输出结果，从事先设计并储存的开关矢量表中选择出所需的三个开关量sj。此控制方法不仅能有效控制有功功率的变化，而且使得稳态时瞬时无功功率基本为零，从而使整流器在单位功率因数条件下工作。

图2 三相电压型PWM整流器DPC系统结构

本文在线检测和计算实际瞬时有功功率和无功功率时采用文献［3］推导出的公式:

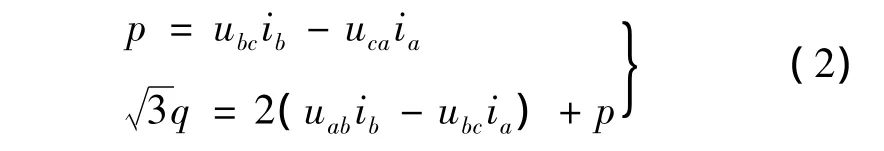
与文献［1］采用的检测和计算方法相比，不仅可以只用两个交流电压传感器与两个交流电流传感器以减少硬件、节约成本，而且避免了三相到两相的静止坐标变换，减少了实时计算工作量。另外，采用这种方法不仅适于三相电压对称的情况，也适于三相电压不对称的情况。因为无论三相电压是否对称，三个线电压之和与三个线电流之和总是零。

2 三相电压型PWM整流器电压环的结构及其改进

文献［1］给出的三相电压型PWM整流器DPC系统的电压环结构如图3所示。

图3 文献［1］的电压环结构图

该电压环由前向通道的5个环节串联而成，分别为惯性滤波环节GLF、PI调节器、作为比例环节的直流电压给定值Udcr、由功率内环近似等效成的小惯性环节Gp(s)和主电路直流侧电阻电容及直流电压给定值构成的大惯性环节Go(s)。各个环节的传递函数表达式如下:

其中的惯性滤波环节本来是为了滤除直流电压反馈值中的纹波，但由于把该环节放在反馈通道中时无法按照“工程设计法”［5］来设计调节器参数，所以才把它移到了前向通道中。然而，这样一来就相当于分别在电压反馈通道与给定通道都加了同样的惯性滤波环节，实际上延缓了电压给定信号，降低了系统响应的跟随性能指标。

为了克服文献［1］给出的上述电压环结构所带来的系统响应跟随性能指标降低的缺陷，本文把惯性滤波环节放在反馈通道中，同时为了提高系统的动态性能，将电压调节器改为PID调节器，然后按照文献［6］提出的“有零点典型I型系统”结构和相应的调节器参数优化设计方法—— 最平幅频法来优化设计调节器参数。其电压环结构如图4所示。

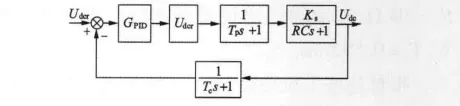
图4 改进的电压环结构图

3 三相电压型PWM整流器电压调节器的优化设计方法

为了提高系统的动态性能，我们将电压环调节器的结构由文献［1］中给出的PI调节器改为PID调节器，其传递函数:

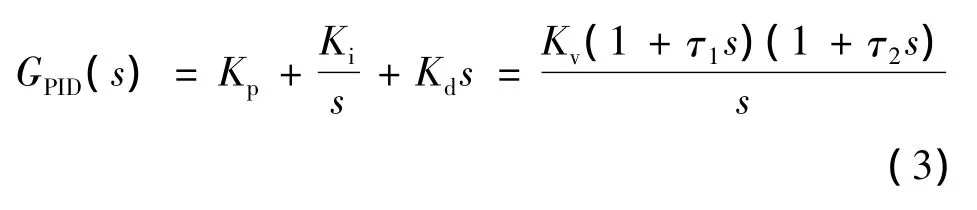
由图4可得到该控制系统电压环的开环传递函数为:

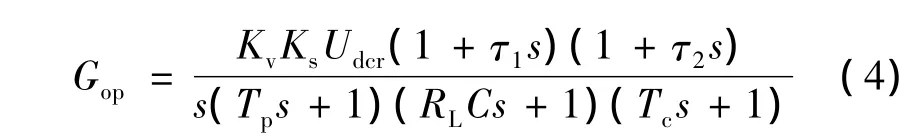
根据零极点对消法［6］，先用电压调节器中的一个零点对消掉时间常数Go(s)中的大惯性，即取τ1=RLC。为了使本方法具有通用性和设计更方便，以Tp为时间基准，将参数进行归一化处理，亦即，令P=Tps，进行复变量代换，则系统的电压环结构如图5所示。图中:

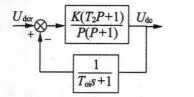
图5 电压环结构图

根据设计“有零点典型I型系统”的最平幅频法，K 和 Toi的函数关系［6］:

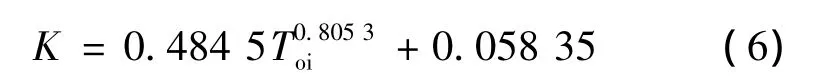
取 Toi=1.1，可以求得:K=0.581 7。

再根据设计这种类型系统的最平幅频法中K、Toi和 T2的函数关系式［6］:

不难求得:T2=1.531 3。

4 三相电压型PWM整流器DPC系统仿真

为了验证上述对电压环的结构改进和调节器优化设计的正确性，我们按照图2的系统结构和下述系统参数采用MATLAB/Simulink软件在电路级进行了仿真。系统参数:三相电源相电压峰值100 V，频率50 Hz，交流侧电感L=10 mH，直流侧电容C=1 100 μF，输出直流电压给定值Udcr=200 V，负载电阻RL=50 Ω，功率滞环比较器滞环宽度Hq=Hp=200 W，Tp=0.592 ms。

根据这些系统参数，由式(5)～式(7)可以计算出PID 调节器参数:Kv=19.65，τ1=55 ms，τ2=0.94 ms。

用Simulink仿真的波形如图6～图8所示。其中图6(a)为按照文献［1］方法设计电压环得出的直流侧电压的波形，而图6(b)为按照本文方法优化设计电压环后得出的直流侧电压的波形;图7为按照本文方法优化设计后得出的网侧A相相电压(图中的纯正弦波)和相电流波形;图8为按照本文方法优化设计后得出的瞬时有功功率(图中峰值较低的波形)和瞬时无功功率波形。

通过图6(a)和6(b)的比较可以看出，采用本文的优化设计方法改进电压环后，系统的动态性能得到显著改善:图6(a)中阶跃响应的超调量σ=22.165%，图 6(b)中阶跃响应的超调量 σ=7.865%;图 6(a)中调节时间 ts=37.35 ms，图6(b)中调节时间ts=17.35 ms(计算调节时间以±5%为稳态误差限)。可见，改进电压环设计后，超调量只有原来的三分之一左右，而调节时间还不到原来的一半。图6中两个直流输出电压在稳态时都稳定在给定参考电压200 V。另外，需要补充的是，文献［1］中的电压环尽管是按照典型Ⅱ型系统设计的，但由于其中的第2个积分环节是用大惯性环节近似而成，所以，其稳态误差度与本文方法设计的电压环一样，仍然是Ⅰ而非Ⅱ。

由图7和图8可以看出，按照本文方法优化设计电压环后，在过渡过程结束后，也实现了三相电压型PWM整流器的网侧电流正弦化且交流相电压与相电流同相，瞬时无功功率稳定在零值附近，系统工作于单位功率因数情况下，瞬时有功功率值稳定在给定值800 W附近。综上所述，仿真结果表明本文的系统电压环优化设计方法可行，且会使系统具有更好的动态性能。

5 结 语

本文对传统的采用DPC策略的三相电压型PWM整流器的电压外环和功率内环(采用滞环比较器控制)控制策略做了两点改进:一是把电压环的惯性滤波环节从前向通道改到了反馈回路中，借以提高系统的快速跟随性能;二是利用最平幅频法优化设计了电压调节器的结构和参数。通过Simulink系统仿真对上述两点改进措施进行了检验，结果表明:采用DPC策略的三相电压型PWM整流器具有调节时间短、超调量小和仍保持单位功率因数等优点。

［1］王久和.电压型PWM整流器的非线性控制［M］.北京:机械工业出版社，2008.

［2］王久和.电压型PWM整流器直接功率控制系统［J］.中国电机工程学报，2006，26(18):54 －60.

［3］卢健康，邢益巽.PWM整流器直接功率控制策略仿真研究［J］.计算机仿真，2012(8):299 －303.

［4］高扬.电气传动自动控制系统优化设计方法研究［D］.西安:西北工业大学，2006.

［5］陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社，2003.

［6］卢健康，王泽峰.双闭环调速系统设计方法的改进及其仿真［J］.系统仿真技术，2010，6(1):29 －32，58.